基于多元特征参数与改进SVM算法的驾驶风格识别研究
黄 江,李雨涵,吴盛斌,丁代林,罗 华,何 渝
(重庆理工大学 车辆学院, 重庆 400054)
0 引言
驾驶风格是指在不同驾驶环境下驾驶员表现出的不同的驾驶特性[1]。激进型的驾驶风格车辆加速度变化较为剧烈,对速度收益的追求程度更高,而保守型的驾驶风格车辆运行更加平稳,对安全收益的追求程度更高。总之,不同驾驶员的驾驶风格对车辆换道有很大的影响,因此,对驾驶风格进行准确识别是有必要的。
传统的驾驶风格识别往往倾向于采用问卷调查得到的数据或车载传感器采集的数据进行[2-3],本文通过对车辆真实的历史轨迹数据进行提取处理,搭建基于多元特征参数的驾驶风格识别模型。
支持向量机(SVM)结构简单,有极强的学习能力和泛用性,可有效避免“维度灾难”,在数据分类、线性回归以及模式识别等方面被广泛应用[4-6]。为对驾驶风格进行识别,郝景贤等[7]利用支持向量机搭建识别模型,得到了较高的识别率,为自适应优化奠定了基础。但在实际应用中,由于传统的SVM模型按固定步长选取参数,可能会导致错过最优解,且当分类类别较多时存在局限性。为了解决上述问题,国内外学者对其进行了改进。在优化支持向量机方面,杨帆等[8]引入了粒子群算法,结果表明,粒子群算法对实时数据处理具有良好的分类效果,但分类的准确性还不够;Xue等[9]也采用了类似的方法,但由于选取参数的离散性,易导致局部最优。李捷辉等[10]利用蝙蝠算法对支持向量机进行优化,建立了预测模型,提高了识别的准确率,但是仍存在运行时间过长的问题;Li等[11]通过遗传算法的自适应性对SVM模型进行参数优化,结果表明该方法准确性较高,但未考虑样本缺失数据的影响;张向东等[12]通过交叉验证对支持向量机的参数进行优化,但未考虑到样本数据较大的情况。
本文在粒子群算法的基础上加入自适应惯性权重ω以优化SVM模型参数。改进的粒子群算法(IPSO)克服了标准粒子群算法(PSO)的缺点,同时也使SVM算法相关参数的选取更加准确,对驾驶风格的识别精度更高。
1 基于改进支持向量机模型的研究
1.1 支持向量机(SVM)算法原理
支持向量机是一种在处理非线性、高纬度等问题时有明显优势的机器学习算法[13],其核心思想是确定一个超平面,使数据点到超平面的距离尽量大,如图1所示。
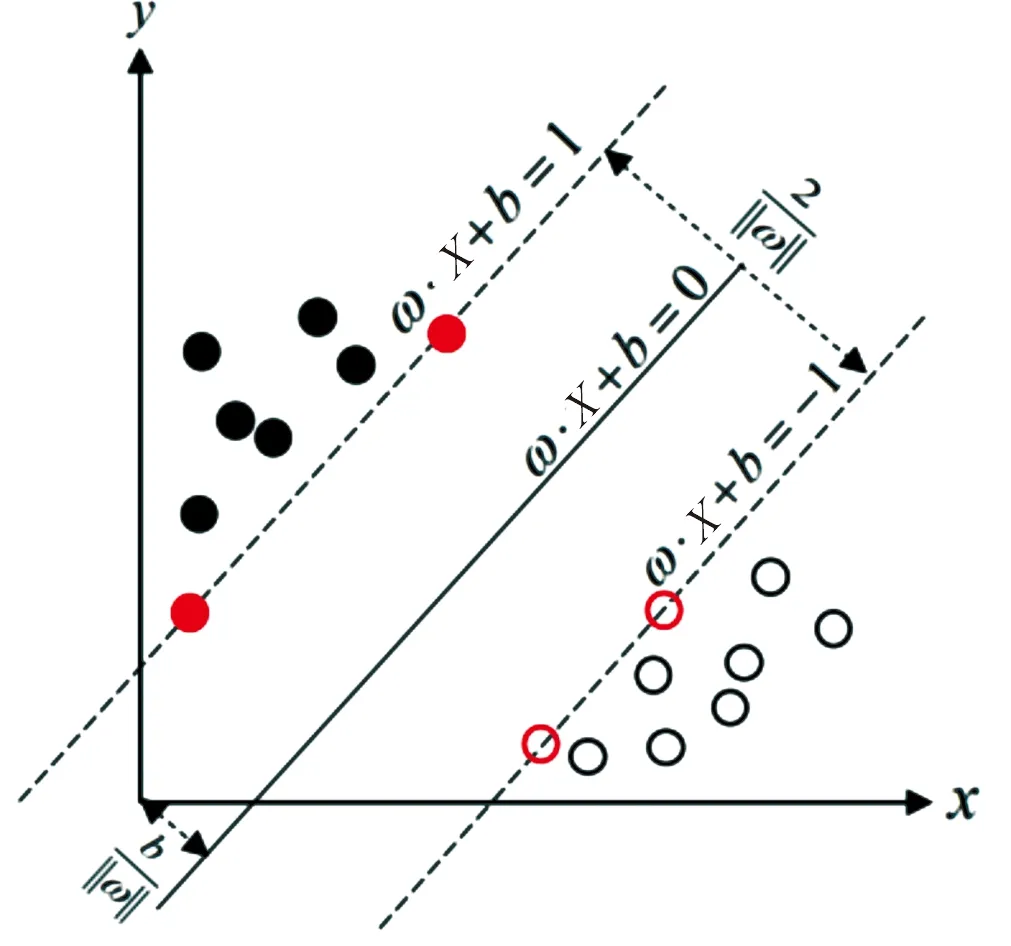
图1 SVM最佳分类超平面


(1)
式中:ω为权重向量;b为偏差;ξi为松弛变量;C为惩罚参数,对模型复杂度和模型训练误差影响较大。
对于非线性数据,SVM算法可以通过非线性变换将其映射到高维度的线性特征空间,以此来构造最佳分类超平面[14]。将有约束的原始目标函数转换为无约束的拉格朗日目标函数,构造拉格朗日方程,得到式(2)所示的对偶拉格朗日算子:
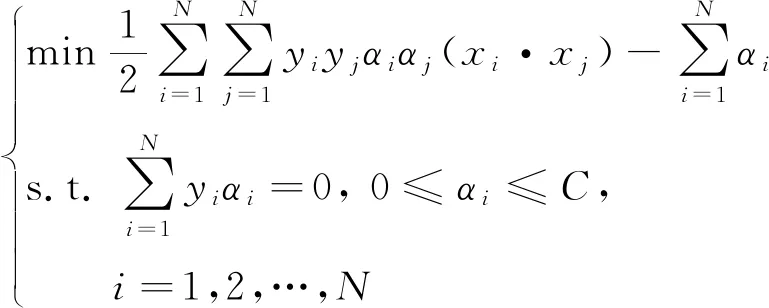
(2)
式中:αi为拉格朗日乘子,且αi>0。最优分类决策函数如式(3)所示。
(3)
式中,sgn(·)代表符号函数,通过函数值的正负可判定样本x的类别。
选择合适的核函数会大大缩短SVM模型的收敛速度、更易得到最优参数。高斯径向基核函数(RBF)可将有限维数据映射到高维空间,其定义如式(4)所示:
(4)
式中:γ为核函数主要参数,影响模型的学习能力,可以反映训练样本数据的范围特性。当γ处于较大值时,SVM模型对训练数据的作用范围较广、识别能力较强,但对于新样本的识别准确性会降低;当γ处于较小值时,SVM模型对样本的作用范围变窄,识别准确性较差,容易造成局部最优,此时的识别函数近似于一个常数。通过RBF核函数,可以得到决策函数,如式(5)所示:
(5)
1.2 改进粒子群(IPSO)算法原理
粒子群算法源自对鸟群觅食行为的研究,其基本思想是将种群中的每个个体都看成没有大小和质量的质点,通过摸拟自然界生物个体之间的信息共享以寻求最优解所产生的一种智能算法,具备和遗传算法相似的优化能力[15]。
传统PSO算法通过跟踪局部最优点和全局最优点来对速度和位置进行更新,如式(6)、式(7)所示。
vi(t+1)=ω(t)×vi(t)+
c1×rand×(pb(t)-xi(t))+
c2×rand×(gb(t)-xi(t))
(6)
xi(t+1)=xi(t)+vi(t+1)
(7)
式中:vi为当前粒子的速度,代表粒子移动的快慢;xi为当前粒子所在的位置,代表粒子移动的方向;ω为惯性权重,通常取值都大于0;pb为局部最优解;gb为全局最优解;c1和c2为两种学习因子,代表每个粒子向pb、gb运动的加速项的权重;随机数rand∈[0,1]。
在全局搜索时需要一个较大的惯性权重,反之,局部搜索需要的惯性权重较小。上述粒子群算法属于全局范畴,具有较快的收敛性,但易造成局部最优,寻找全局最优解的能力较弱。针对上述问题,相关学者展开了研究。部分学者在迭代过程中引入了线性递减的惯性权重,相比于固定的惯性权重,该方法可以较好地提高算法的性能,对全局寻优和局部寻优能力进行调节,但是该方法存在一定的局限性,由于PSO算法的寻优过程是非线性的,所以线性的惯性权重不能真实地反应粒子的寻优过程,使最终效果并不理想。还有学者引入了非线性递减的惯性权重,如指数形、S形等,这种方法可以有效平衡迭代过程中全局搜索和局部搜索的能力,但是忽略了算法后期震荡严重的缺陷,会对算法后期的收敛速度造成一定的影响。
1) 当f(xi)>f(pb)时,在迭代初期理论上粒子处于局部最优状态。此时需要赋予粒子一个较大的惯性权重,当搜索面积较大时,最大化地进行全局寻优,加快其收敛速度,有助于确定最优解的大概区域,惯性权重计算如式(8)所示:
(8)
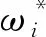
(9)
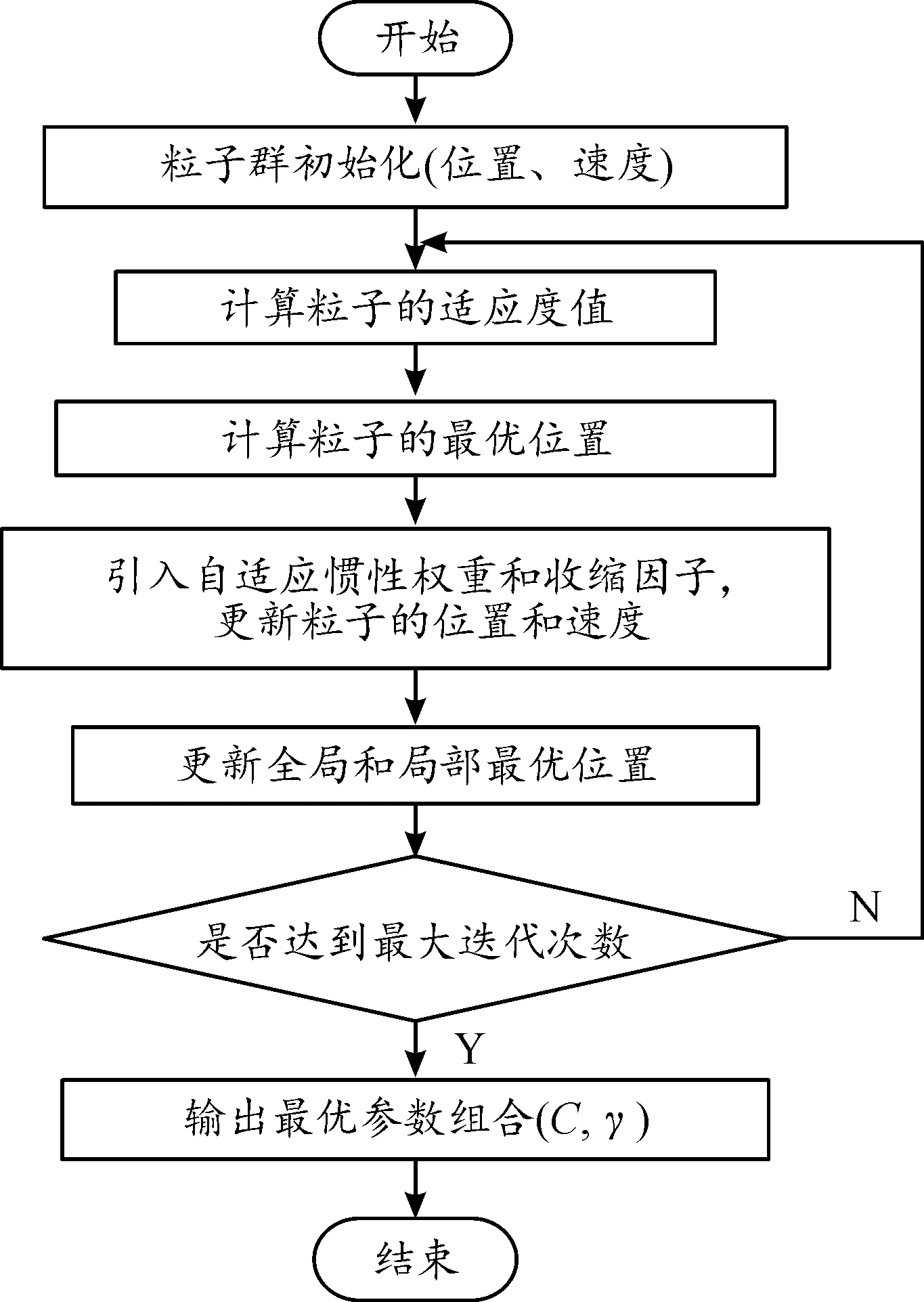
3) 当f(xi) (10) 式中:ωmax和ωmin分别为最大与最小惯性权重;K为最大迭代次数;k为当前迭代次数;随机数rand∈[0,1];f(xi)为粒子当前的适应度值;f(pb)为粒子处于局部最优解时的适应度值;f(gb)为粒子处于全局最优解时的适应度值。粒子适应度越小,粒子距离最优解越远,此时需要进行全局寻优。与基本粒子群算法相比,现在的惯性权重与迭代次数和每个粒子的适应度都有关。 针对非线性数据的识别,支持向量机模型增加了松弛变量ξi以减小轻微误差带来的影响,通过惩罚参数C可以调节松弛变量ξi。C增大时,ξi减小,对错误的容忍度减小,泛化能力变弱,对样本的识别准确率增加,但当其过大时会由于样本极端化造成过拟合;C减小时,ξi增大,对错误的容忍度增大,泛化能力增强,可以得到较大的分类间隔,但当其过小时可能由于无法得到最优解而造成欠拟合。因此,为了避免惩罚参数C达到极值造成算法的过拟合或欠拟合,同时兼顾分类间隔最大化与样本识别的准确率,对惩罚参数C的适当选取是非常有必要的。 当使用高斯径向基核函数时,其参数γ承担主要映射作用。当γ越大时,映射维度越高,映射样本空间越分散,识别的准确率越高,但由于其支持向量减少,造成模型的训练和测试速度降低;反之,当γ越小时,映射维度越低,支持向量增多,模型训练和测试速度越快,但由于映射样本空间过于集中,导致样本识别的准确率降低。因此,为了平衡识别准确率与模型训练速度之间的关系,必须要选择恰当的核参数γ。 综上所述,需要着重考虑惩罚函数C和核函数参数γ的取值问题,确定最优参数组合(C,γ),以提高SVM模型的收敛速度和识别准确性。本文采用改进的粒子群算法对SVM模型进行优化,具体如下所示: 步骤1:初始化SVM模型参数、IPSO算法参数。随机初始化待优化参数惩罚函数C和核参数γ参数组合(C,γ),随机初始化其位置和速度信息,初始化种群数量N=20,最大迭代次数K=150。 步骤2:计算粒子寻优的适应度值。将粒子位置、速度等信息代入适应度函数f(xi),通过适应度函数来评定SVM模型的收敛性和准确性,本文选取均方误差作为其适应度函数。 步骤3:确定最优值。找到初始信息下个体粒子的最优位置和整个粒子群的最优位置。 步骤4:更新位置和速度。引入自适应惯性权重ω*,比较当前粒子适应度f(xi)与粒子处于局部最优解时的适应度值f(pb)及粒子处于全局最优解时的适应度值f(gb)的大小,根据式(8)—(10)进行更新调整。按照式(11)更新粒子的速度信息,其中,个体学习因子c1=1.5,社会学习因子c2=1.7,最大惯性权重ωmax=0.91,最小惯性权重ωmin=0.39。 vi(t+1)=ω*(t)×vi(t)+ c1×rand×(pb(t)-xi(t))+ c2×rand×(gb(t)-xi(t)) (11) 步骤5:更新最优值。通过位置和速度的最新状态来更新当前粒子的最优位置Pi和整个群体的最优位置Pg,找到个体最优和全局最优粒子。 步骤6:判断是否达到最大迭代次数。当达到K时结束循环,输出最优参数组合(C,γ),反之,重复上述步骤直至满足条件。 步骤7:利用最优参数组合(C,γ)建立SVM识别模型。 具体流程如图2所示。 图2 IPSO-SVM算法流程框图 通常为了验证优化后SVM模型的各项性能,都会采用UCI公共数据集进行测试[16-17]。选择UCI数据集的wine、iris、seeds、breast-tissue 作为样本对其进行验证。对应各数据集信息如表1所示。 表1 各数据集相关信息 通过与文献[16,18]中交叉验证优化的支持向量机模型(CV-SVM)、标准粒子群算法优化的支持向量机模型(PSO-SVM)相比较的方法来验证改进粒子群算法优化支持向量机模型(IPSO-SVM)的识别效果。其中,惩罚函数C的取值范围为(0.1,100],核函数参数γ的取值范围为[0.1,10]。各模型的识别精度、均方误差及运行时间如表2所示,适应度曲线如图3所示。 根据表2中各结果数据分析可知,对于数量、维度均不同的数据集,IPSO-SVM识别模型的准确率均高于其他2种,均方误差均小于其他2种,平均运行时间均有所减少,证明了优化后的IPSO-SVM模型相比于传统的CV-SVM模型和改进前的PSO模型都有更好的识别效果,且时效性更好。 表2 各模型识别准确率与均方误差 根据图3可知,优化后的SVM模型在迭代初期下降得更快,说明模型是从全局最优解附近开始寻优,加快了前期的收敛速度;寻优时的迭代次数明显少于其他模型,使模型的收敛速度更快,收敛精度更高;同时迭代过程中曲线变化更为平坦,说明改进后的模型稳定性更好。 图3 各数据集适应度曲线 选取NGSIM(next generation simulation)数据[19]进行研究,该数据集采集了通过目标区域所有车辆的时空信息,并以0.1 s间隔进行输出,具有较高的准确性。 本文设定以下条件对车辆轨迹数据进行筛选:仅选用小汽车作为研究对象;仅考虑自由换道、单次换道的车辆;仅提取换道车辆目标车道后车的相关数据;排除两车相对距离大于30 m小于5 m的数据信息。以ID=15的车辆为例,筛选数据如表3所示。 表3 NGSIM部分筛选数据 由于NGSIM数据集中的车辆行驶数据是通过视频处理技术获得的,存在大量噪声和异常点,如果不进行数据清洗,在计算速度和加速度时误差会被放大,影响模型的准确性。针对上述问题,采用对称指数移动平均法对数据进行平滑处理[20]。在筛选得到的行车数据的基础上,通过反复对平滑窗口进行测试对比其平滑效果,获取最终平滑表达式。以ID=15的车辆行驶数据为例进行平滑处理,其纵向位置、速度、加速度的平滑效果如图4所示。 通过图4平滑处理前后车辆的运动数据对比可以看出,相比于原始数据,平滑后的数据在完整保留车辆驾驶行为特性的同时,剧烈抖动衰减明显,车辆行驶状态更为平稳,更符合车辆实际的运行状态。 图4 数据平滑处理曲线 为了对驾驶风格进行更好的描述,需要选取驾驶风格相关特征数据。通过对与驾驶行为相关的多元特征参数进行统计学分析,最终选取6个作为评价指标,如表4所示。 表4 评价指标选取 降维是主成分分析法的主要思想,可将高维空间的数据点映射到低维空间。采用主成分分析法将8个评价指标降维成几个主成分,每个主成分都可以综合反映8个评价指标的信息并且每个主成分都线性不相关,一定程度上减少了信息重叠,大大缩短了训练时间。 在主成分求解之前,对数据进行归一化处理可以有效地消除量纲之间的差异,将每个特征参数对应的数据都转换到0~1之间。将归一化处理后的数据作为主成分分析的输入。数据进行线性映射之后,需要根据各成分的重要度排序,并根据累计方差贡献率判定主成分[21],计算如式(12)所示。 (12) 式中:G(k)为累计方差贡献率;λ为特征值。 图5为各主成分的方差贡献率和累计方差贡献率。方差贡献率排名前三的主成分的累计方差贡献率超过了85%,因此,可以选择前3维数据作为6个评价指标的线性组合,进行后续的分析。 图5 方差贡献率及累计方差贡献率 得到的3个主成分能够很好地反映原始指标所代表的信息,将其作为聚类分析及识别模型的输入。主成分Y1、Y2、Y3可以通过评价指标Xi(i=1,2,…,6)计算得到,如式(13)所示。 (13) K-means算法是一种将欧式距离作为数据相似性评价指标的非监督学习算法,使用数据驱动的方法,获得驾驶员在驾驶风格类别上的归属性,聚类得到的结果可以作为识别模型的标签使用[22]。 为得到理想的聚类效果,依次将聚类中心设置为2中心、3中心和4中心,聚类结果如表5所示。 表5 K-means聚类结果 当聚类数目为2时,两类样本数量之间相差较大,且第一类簇的样本数量达到了总样本数量的87%,超过了60%,造成了欠分类问题;当聚类数目为3时,各类簇之间的差距开始变小,且各类簇的样本数量都较为合理;当聚类数目为4时,类簇间的差距进一步变小,但是第一类簇和第三类簇的样本数量相比总样本数量都已经少于15%,造成了过分类问题。综上所述,将驾驶风格分为3类聚类效果最优,结合人们对驾驶风格的定性认知以及3种驾驶风格对应特征参数值的大小,可以判断3种驾驶风格依次为保守型、普通型和激进型。 如图6所示,为3种驾驶风格的聚类结果。各主成分可以清晰地被划分为3类,第一类为保守型,聚类中心坐标为(-0.23,0.27,0.49);第二类为普通型,聚类中心坐标为(0,0.08,0.48);第三类为激进型,聚类中心坐标为(0.21,0.4,0.05)。针对于不同的数据,K-means算法可以实现有效地聚类,将聚类结果作为后续识别模型的输出。 图6 K-means聚类结果 从NGSIM数据库中选取Peachtree数据集作为仿真样本,对改进的IPSO-SVM识别模型进行训练和测试,其中Peachtree数据集是美国佐治亚州亚特兰大市的城市道路数据。具体样本数据如表6所示。 表6 样本数据 IPSO-SVM模型对驾驶风格进行识别的过程如图7所示。 图7 IPSO-SVM模型驾驶风格识别过程框图 1) 对样本数据进行处理,确定模型的输入和输出。将主成分分析法得到的主成分[Y1、Y2、Y3]作为模型的输入,将K-means聚类算法得到的驾驶风格类型作为模型的输出。 2) 核函数选择。本文选取高斯径向基核函数作为模型的核函数。 3) 数据集划分。按7∶3将样本数据划分为训练集和测试集。选取70%的样本数据作为SVM的训练样本,选取剩余数据作为验证样本,对未训练的轨迹数据进行测试。 4) 参数优化。采用IPSO算法对SVM模型的惩罚函数C和核参数γ进行优化,得到最优参数组合(C,γ)。 5) 模型训练。分别对采用传统交叉验证方法的CV-SVM模型、未改进的支持向量机模型PSO-SVM和改进的支持向量机模型IPSO-SVM进行训练,使用带类别标签的特征[Y1、Y2、Y3、sort],其中sort为不同驾驶风格的类别标签,其中1为保守型,2为普通型,3为激进型。 6) 模型验证。为了验证所建模型的精度和可靠性,将测试结果与实际值相比较,采用识别精度、均方误差(MSE)、平均绝对误差(MAE)、运行时长和ROC曲线作为评价标准来评判模型的效果。MSE和MAE计算如式(14)(15)所示。 (14) (15) 对改进的IPSO-SVM识别模型进行仿真分析,得到如图8—10所示的分类结果。从图中可以直观地看出:CV-SVM、PSO-SVM、IPSO-SVM 3种模型的错误识别样本。 图8 CV-SVM识别模型识别结果 如图8所示,CV-SVM识别模型错误识别样本较多,主要集中在第二类即普通型驾驶风格区域。与该模型相比,PSO-SVM模型错误识别样本相对减少,如图9所示。IPSO-SVM模型错误识别样本最少,准确率最高,如图10所示。 图9 PSO-SVM识别模型识别结果 图10 IPSO-SVM识别模型识别结果 表7是关于各识别模型的相关结果,图11是各识别模型的适应度曲线。从图表中可以看出:在识别精度方面,IPSO-SVM模型的识别精度最高,平均可达97.96%,相比CV-SVM模型识别精度提高11%,与PSO-SVM模型相比识别精度提高4%;在误差方面,IPSO-SVM模型的均方误差比CV-SVM模型降低88%,比PSO-SVM模型降低80%;平均绝对误差比CV-SVM模型降低87%,比PSO-SVM模型降低75%;在运行时间方面,IPSO-SVM模型的平均耗时相比于CV-SVM和PSO-SVM模型分别减少了32%、28%,收敛速度最快,时效性最好;在收敛性方面,IPSO-SVM模型能够更加快速地完成收敛,减少迭代次数,曲线也较为平稳,使其收敛速度、收敛精度及稳定性方面均优于其他2种模型。 表7 各模型识别驾驶风格的结果 图11 各模型识别驾驶风格的适应度曲线 根据上述分析,可以得到3种模型驾驶风格识别时关于准确性、时效性及收敛性等方面的差异,其中本文搭建的IPSO-SVM模型效果均最优。对于不同类型的驾驶风格,分类讨论其识别效果,如表8所示。 表8 不同驾驶风格下各模型的识别精度 由表8可知,无论是保守型、普通型或激进型驾驶风格,IPSO-SVM模型的识别精度都优于其他2种模型,收敛速度更快,尤其是保守型和激进型驾驶风格,识别精度甚至达到了100%,但由于本文在选取数据时一系列筛选条件的限制,使实验样本数量偏少,导致结果的差异性不是很明显,在后续的研究中会进行改进。 进一步通过ROC曲线和AUC值对不同驾驶风格下识别模型的性能和可靠性进行分析。 如图12—14所示,在进行驾驶风格识别时,无论是保守型、普通型或激进型,IPSO-SVM模型的AUC值都最大,PSO-SVM模型次之,CV-SVM模型最小,说明与CV-SVM算法和PSO-SVM算法相比,IPSO-SVM模型的识别性能都更优,识别能力更强,可靠性更好。 图12 保守型驾驶风格下各模型的ROC曲线 通过对不同模型及不同驾驶风格类型的识别精度、误差率、运行时间和ROC曲线的AUC值对比分析可知,相比于交叉验证和未改进的支持向量机模型而言,本文搭建的改进粒子群算法优化支持向量机模型的准确性最高,时效性和收敛性最好,有更强的识别能力和更好的可靠性。 图13 普通型驾驶风格下各模型的ROC曲线 图14 激进型驾驶风格下各模型的ROC曲线 本文通过优化粒子群算法,提出了一种基于改进PSO算法优化SVM参数的驾驶风格识别模型。通过对NGSIM数据库多元特征数据处理,进行仿真对比实验。结果表明:与CV-SVM模型和PSO-SVM模型相比,IPSO-SVM模型克服了易陷入局部最优的缺点,有效提高了识别准确率,减小了误差,加快了收敛速度,其准确率可达97.96%,均方误差减小约88%,平均绝对误差降低约87%,运行耗时平均减小30%,同时通过ROC曲线和AUC值更一步证明了模型的性能和可靠性。综上,在驾驶风格识别方面,本文搭建的IPSO-SVM模型是可行的。1.3 IPSO算法对SVM模型的优化
1.4 模型验证



2 数据处理
2.1 数据来源
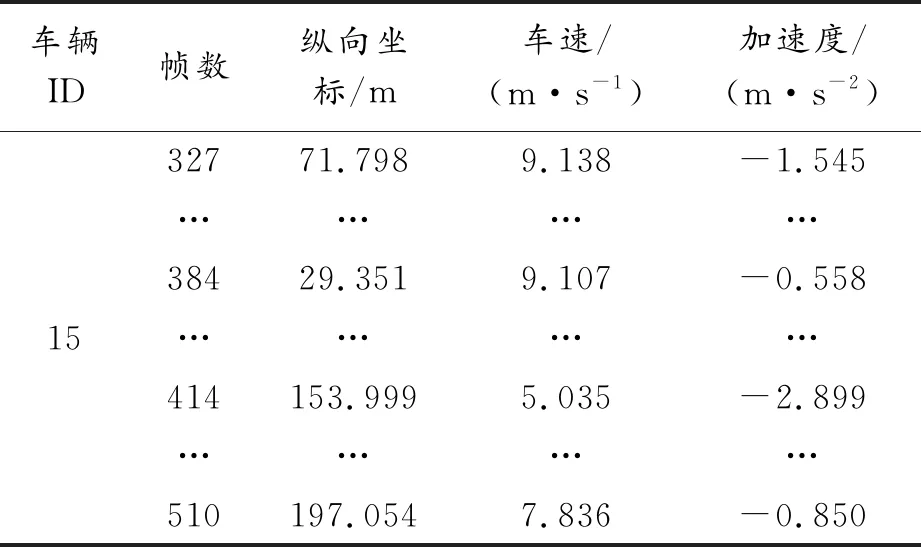
2.2 数据清洗
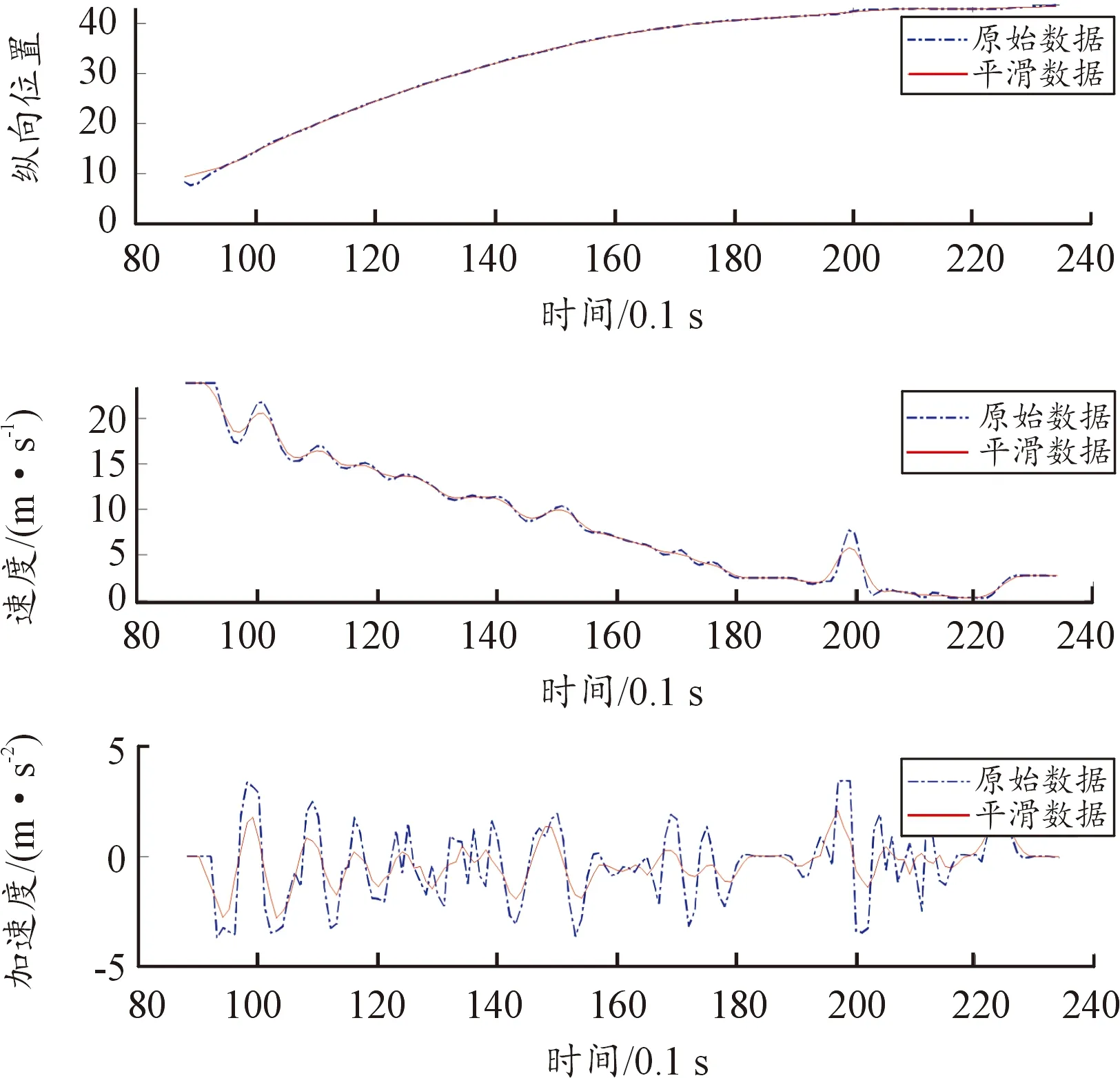
2.3 主成分分析法


2.4 K-means聚类


3 驾驶风格识别模型研究
3.1 基于IPSO-SVM的驾驶风格识别模型



3.2 结果分析






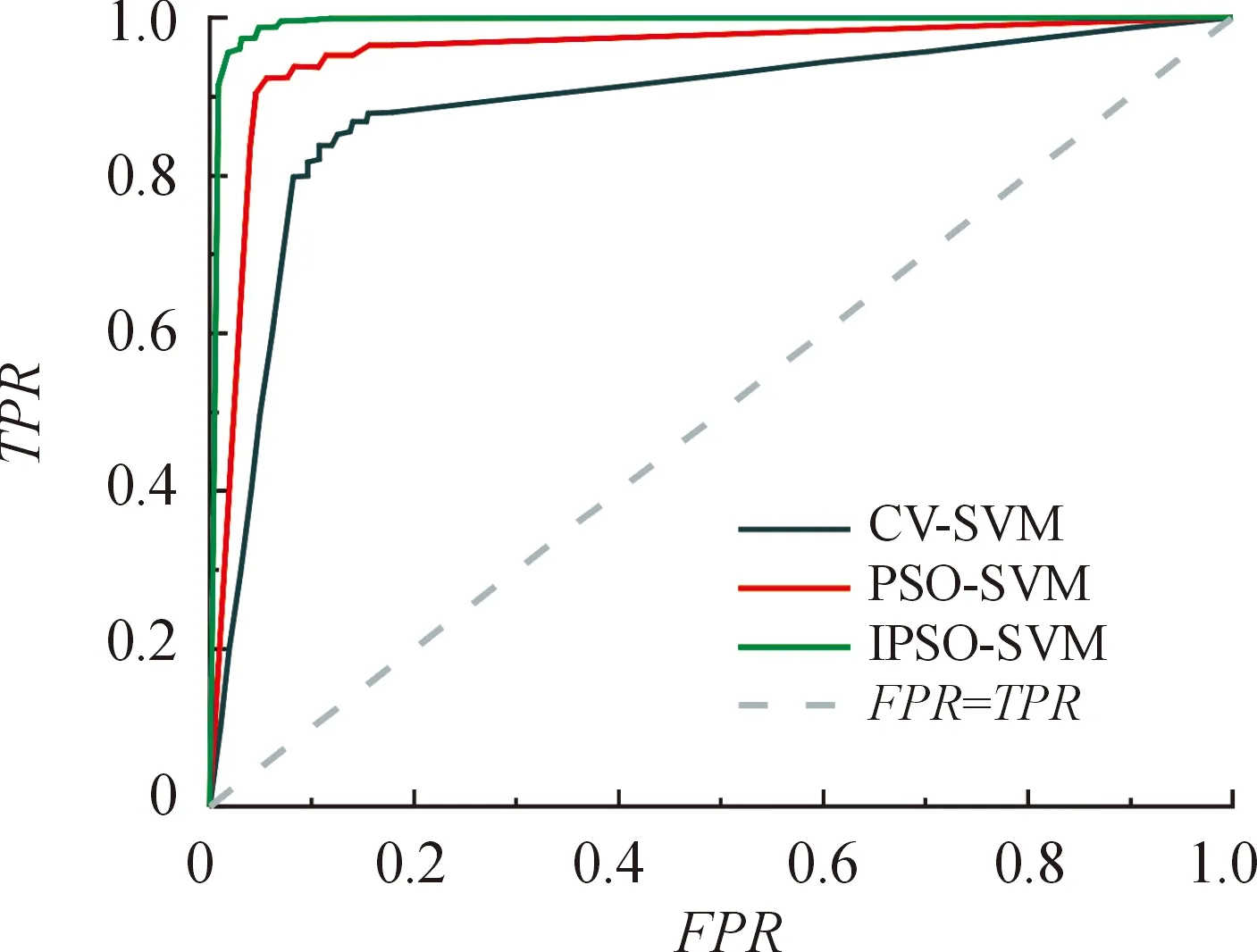

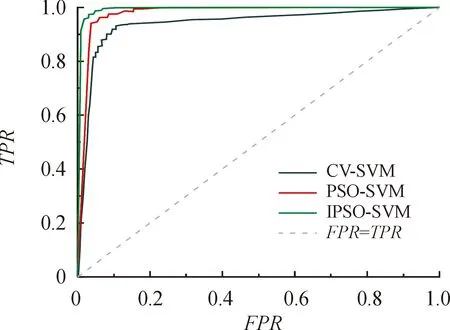
4 结论

