基于自适应差分进化算法优化的主动悬架单神经元PID控制
焦 蕊,赵 强,谢春丽,李哲煜
(东北林业大学 交通学院, 哈尔滨 150040)
0 引言
悬架是车辆的重要总成之一,能够传递车轮和车身之间的一切力和力矩,处在地面和车身之间,是振动和噪声的传递器,衰减由路面不平度产生的振动冲击[1]。被动悬架的刚度和阻尼系数是固定不变的,只能应用在一定频率范围内,无法根据路面实际状况进行实时调节。与被动悬架相比,主动悬架能够根据实际路面的激励自动调节悬架系统的参数,产生反作用力用于抵消路面激励,削弱地面对汽车的冲击,减小车身颠簸,提高汽车行驶平顺性与舒适性[2]。主动悬架的控制策略对主动悬架的性能有很大影响。其中,PID控制结构简单,可操作性强,适用范围广且具有良好的控制效果和鲁棒性。然而其对非线性、时变性系统或受外界干扰系统难以达到高精度的控制要求[3]。所以,单纯的PID控制效果不佳。为了克服PID控制主动悬架上所存在的一些问题,可以与如神经网络[4]、模糊控制[5]等其他控制方法联合使用[6]。神经网络具有自适应、自学习的能力,适合求解复杂的非线性问题[7]。其中,单神经元作为神经网络最基本单元,模型简单,鲁棒性强。将单神经元与PID控制结合,既能克服传统PID随动性差的缺点,又保留了其结构简单、易于实现、可靠性高等优点[8]。单神经元PID控制可以根据对控制器的权值进行在线调整,但其中的增益K和比例、积分学习速率ηP、ηI、ηD需要根据实际情况进行设定,要选择控制效果最佳的参数,所以参数调节上也存在一些困难。目前有些文献上提出用模糊算法调节单神经元PID控制[9]、遗传算法优化单神经元PID控制[10]和连续蚁群算法优化单神经元PID控制[11]等方法,均能改善单神经元PID的控制性能,但其中都未考虑路面脉冲和车辆簧载质量参数变化的影响。
在进化算法中,差分进化算法具有结构简单、参数少、收敛性好和搜索能力强的特点,因此,很多研究者将差分进化算法与约束处理技术结合来求解约束优化问题[12],差分进化算法相对遗传算法的逼近效果更加显著且降低了算法的时间复杂度[13]。本文针对主动悬架,为提高乘坐舒适性,以车身垂直加速度为主要评价指标,采用自适应差分进化算法优化单神经元PID控制器。并且在文中考虑路面脉冲输入和车辆簧载质量的变化,建立Matlab/Simulink模型,测试和验证优化后模型的效果。
1 悬架建模
为方便分析车辆主动悬架系统,将复杂的悬架系统简化成如图1所示的模型。简化后的模型仅分析垂向自由度。垂直自由度为影响汽车舒适性性能最关键因素之一[14]。并且可以通过建立模型仿真得出车身垂直加速度参数的变化,从而更好地控制车身在纵向上的振动,来保证更好的乘坐舒适性。

图1 1/4二自由度主动悬架结构示意图
根据牛顿第二定律可以得出

(1)
式中:m1为非簧载质量;m2为簧载质量;k1为轮胎径向刚度系数;k2为悬架刚度系数;c为减振器阻尼系数。


(2)
Y=CX+DU
(3)

2 单神经元PID控制
2.1 PID控制器
PID控制是一种传统控制方式,在工业上应用非常广泛。如图2所示,PID控制器基于实际输出值与期望值的相对误差,通过将比例、积分、微分3种变量用线性组合方式构成控制量,并将其作用于相对误差,从而实现对被控对象的控制作用,得到期望的输出值。

图2 PID控制器系统框图
根据图2,PID的控制规律可写作:
u(t)=Kp((r(t)-y(t))+
(4)
2.2 单神经元PID控制
单神经元PID控制是将神经网络基本思想与PID控制相结合,其弥补了传统PID调节复杂非线性系统时自适应性的不足,同时还具有结构简单、易操作的特点。单神经元PID控制可对常规PID算法中的比例、积分、微分3个参数进行在线自适应调整,提高了系统响应速度和适应能力,其具体结构参见图3。

图3 单神经元PID 控制结构示意图
图3中,转换器将设定值与实际输出值的偏差量转换成单神经元控制所需的状态量:

(5)
单神经元自适应PID控制器采用有监督的Hebb学习规则的控制算法和学习算法:
(6)

(7)
式中:K是神经元比例系数,一般取K>0,单神经元PID系数ω1、ω2、ω3可以通过神经元的自适应学习能力进行在线调整:

(8)
式中:ηP、ηI、ηD分别为比例、积分、微分的学习速率。
式(6)中,增益K对系统起着十分重要的作用,传统的单神经元PID控制器的神经元比例系数K不支持在线调整。K值过大,则超调量变大、系统不稳定。K值过小,则系统的快速性变差[15],通过Matlab/Simulink仿真建模实验得出,当K值超过一定界限,调整ηP、ηI、ηD的初始参数,增大K值,控制量效果越好且超调量接近于0,系统控制效果稳定。所以,K值的选择很重要,需要进行多次实验选择出最适合的K值。在调节K值的同时,还要使最终控制效果良好,防止系统不稳定,无法收敛。
3 基于自适应差分进化算法优化单神经元PID
3.1 差分进化算法
差分进化算法是一种基于群体差异的智能优化算法,通过模拟生物群体内个体间的合作与竞争产生的启发式群体智能来指导优化搜索。差分进化算法的群体由变异、交叉和选择过程筛选出来。
差分进化算法过程如下:
1) 初始化种群

xi(g)=(xi,1(g),xi,2(g),…,xi,n(g))
i=1,2,…,NP
(9)
在D维空间里随机产生满足约束条件的NP个染色体,第i个染色体的第j个维取值方式如下(rand(0,1)产生0到1的均匀分布的随机数):
(10)
2) 变异
差分进化算法是在遗传算法的基础上提出的,主要通过差分策略实现变异操作,这是差分进化算法的最大特点。在第g次迭代中,对于个体Xi(g)=(Xi,1(g),Xi,2(g),…,Xi,n(g)),从种群中随机选择3个不同的个体Xp1(g)、Xp2(g)、Xp3(g),且p1≠p2≠p3,则
Hi(g+1)=Xp1(g)+F(Xp2(g)-Xp3(g))
(11)
式中:F是变异算子,用于控制差分向量的影响力。

3) 交叉
交叉操作可以增加物种的多样性。对于第g代种群xi(g)及其变异产生的Hi(g+1)进行交叉操作:

(12)
式中:cr∈[0,1]为交叉概率,rand(0,1)是[0,1]上服从均匀分布的随机数。
4) 选择
查看评价函数选择Vi(g)或Xi(g)作为Xi(g+1):

(13)
3.2 自适应差分进化算法
差分进化算法的变异算子F是人为确定的实常数,在优化过程中,较难确定一个最优参数。在变异操作中,变异算子F用于控制差分向量的影响力。如果F取值为常数,F过大,则会导致算法的收敛速度变慢,所求全局最优解精度降低。若选取F过小,会导致种群的多样性降低,易出现早熟现象,所以在自适应差分进化算法中将参数F设置为一个随着迭代次数变化进而变化的值。
自适应算子表示为
(14)
式中:G为最大迭代次数,gen为当前迭代次数。
变异算子F表示为
F=F0·(3/2)λ
(15)

图4 差分进化算法寻优曲线和自适应差分进化算法寻优曲线
2个算法各独立运行40次后,对各自优化得到的40个目标函数值分别取平均值,自适应差分进化算法目标函数平均值为0.021,差分进化算法目标函数平均值为0.027。改进幅度为22.22%。可以得出,自适应差分进化算法比差分进化算法收敛效果更好,响应更快,精度更高。故选择自适应差分进化算法对单神经元PID进行优化。
3.3 自适应差分进化算法优化单神经元PID控制器
由于单神经元PID控制系数确定具有主观性,所以采用自适应差分进化算法对单神经元PID控制器K、ηP、ηI、ηD共4个参数进行优化,目标函数为
J=|rms(e(k))|
(16)
算法优化过程如下:
1) 设定学习速率ηP、ηI、ηD和神经元比例系数K的初始取值范围。确定初始种群规模大小,确定交叉算子和初始变异算子;
2) 生成初始种群;
3) 计算每次循环中目标函数;
4) 利用自适应差分进化算法函数寻优。找到最优的学习速率ηP、ηI、ηD和神经元比例系数K参数值;
5) 采用优化后的参数进行仿真。
具体的自适应差分进化算法优化单神经元PID的伪代码如下:
fori←1 toNPdo
forj←1 toGdo
end for
end for
g←1
while stopping criteria not met do
fori←1 toNPdo
r(1,2,3)←getlndexs(NP)
forj←1 toGdo
F←F0·(3/2)λ
ifrandu[0,1]≤crorj=jrandthen
else
end if
end for
Call single-neuron PID model to compute
else
end if
end for
g←g+1
end while
4 仿真结果与分析
在Simulink中建立被动悬架、PID控制、单神经元PID控制和自适应差分进化算法优化单神经元PID控制的仿真模型,通过改变簧载质量和路面输入来验证优化模型的有效性。首先以B级路面作为输入考察控制效果,路面输入采用白噪声法的路面时域激励模型。滤波白噪声路面不平度时域模型为
(17)
式中:n1为下截止频率;Gq(n0)为路面不平度系数;为车辆行驶速度;q(t)为数学期望为零的高斯白噪声;n0为参考空间频率。
对应B级路面,取n1为0.01 Hz。在Simulink中建立路面输入模型,运行模型,得到B级路面位移仿真结果,如图5。

图5 B级路面位移仿真结果
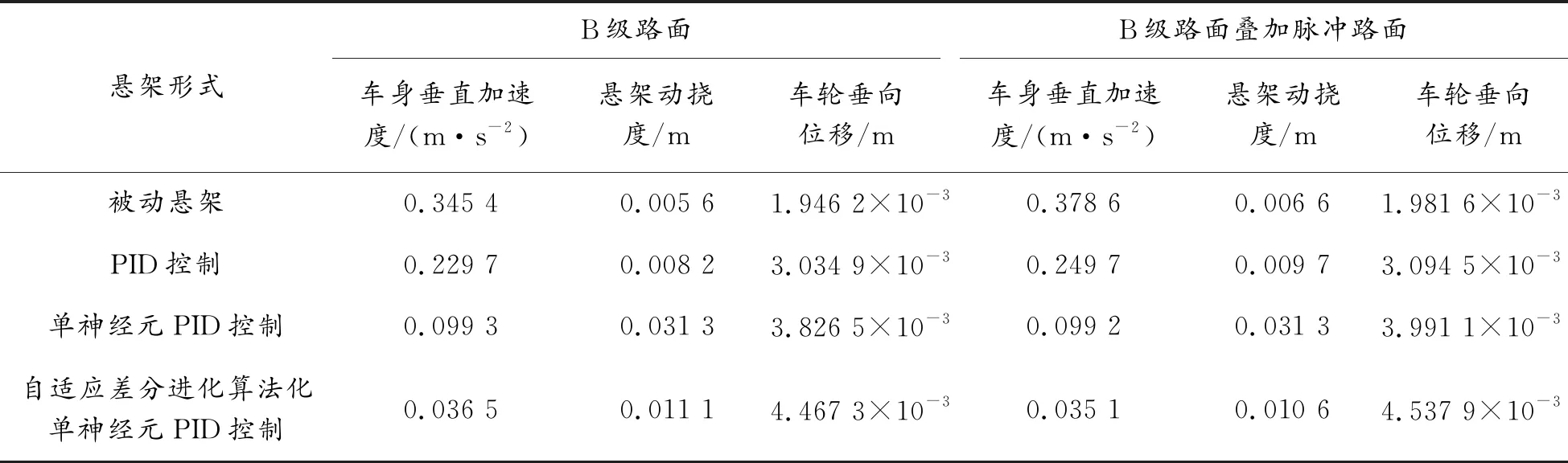
表2为车辆状态参数,图6为以车辆半载和随机路面为模型的自适应差分进化算法优化目标函数曲线,优化结果为K=9 852.3,ηP=4 197.6,ηI=1 459.9,ηD=55.1。将优化后得到的参数输入到单神经元PID控制悬架模型中进一步仿真。图7为车辆半载时车身垂直加速度曲线。图8为车辆满载时车身垂直加速度曲线。图9为车辆空载时车身垂直加速度曲线。

表2 车辆状态参数

图6 自适应差分进化算法目标函数曲线

图7 B级路面车辆半载时车身垂直加速度曲线

图8 B级路面车辆满载时车身垂直加速度曲线
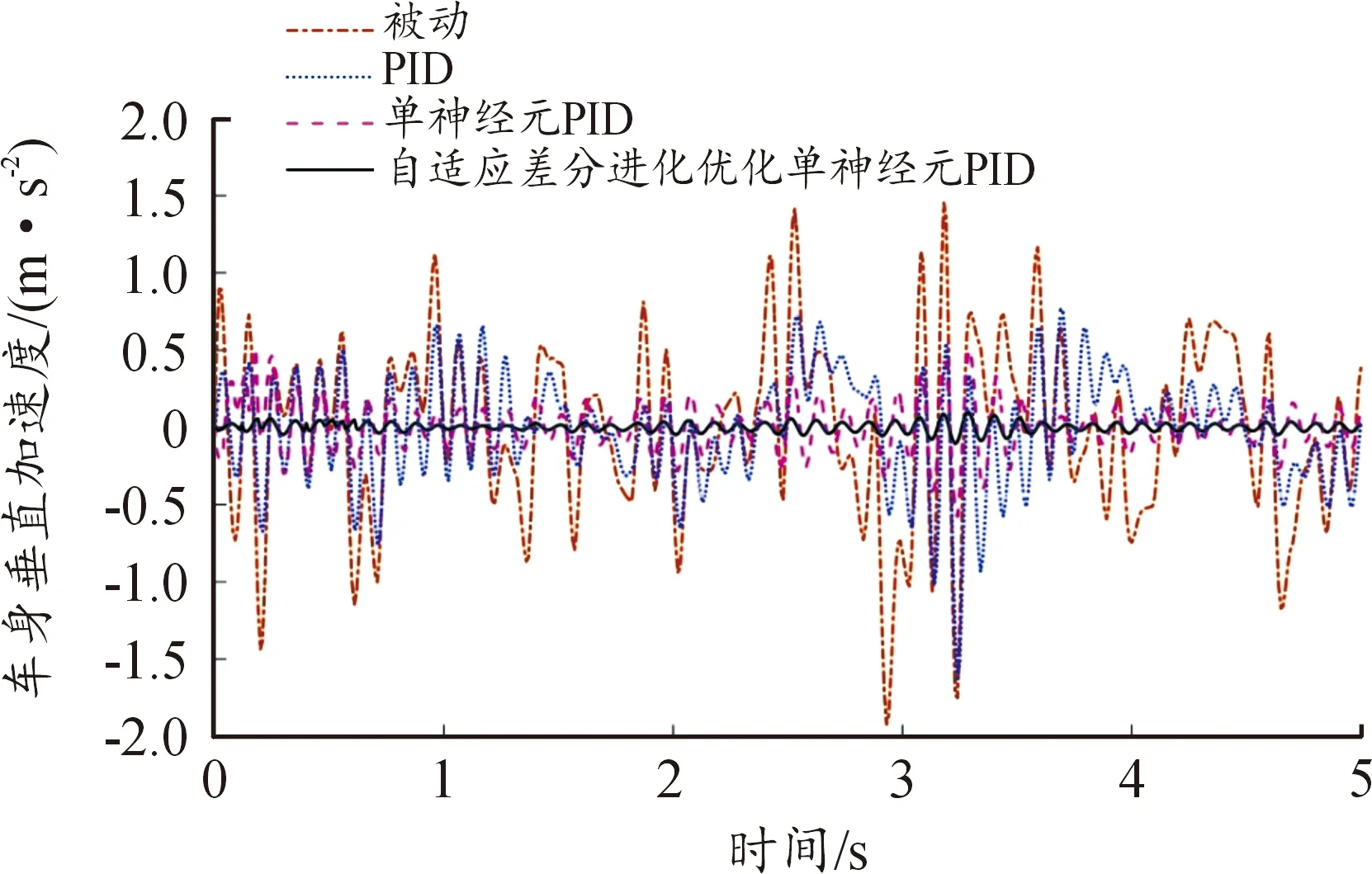
图9 B级路面车辆空载时车身垂直加速度曲线
进一步利用路面凸包考察控制算法在系统受到外界扰动下的鲁棒性,路面凸包采用脉冲路面输入来模拟,其是来自路面的偶然、短时间的冲击性的位移变化,通常即是由正常路面上的包或坑等原因产生的。因此,可以看作是脉冲信号输入。本文采用一个B级路面叠加单凸包作为脉冲路面输入
(18)
式中:A=0.05 m,表示在2 s 图10 B级路面叠加凸包输入路面位移仿真结果 图11为车辆半载时车身垂直加速度曲线。图12为车辆满载时车身垂直加速度曲线。图13为车辆空载时车身垂直加速度曲线。 图11 B级路面叠加凸包输入路面车辆半载时车身垂直加速度曲线 图12 B级路面叠加凸包输入路面车辆满载时车身垂直加速度曲线 图13 B级路面叠加凸包输入路面车辆空载时 根据仿真试验在不同簧载质量和路面情况下的悬架控制效果,最终得出悬架评价指标均方根值,如表3— 5。表6为自适应差分进化算法优化单神经元PID控制与PID控制的主动悬架的车身垂直及速度优化幅度。从表3— 6可以看出,在不同路面下,车身垂直加速度均明显降低,平均优化幅度在80%以上,悬架动挠度和车轮垂向位移在优化后略微升高,但依然在安全范围以内,悬架结构空间决定其动行程允许范围在70 mm内[16],可以证明自适应差分进化算法可以有效降低车身垂直加速度,改善乘坐舒适性。 表3 半载时悬架评价指标均方根值 表4 空载时悬架评价指标均方根值 表5 满载时悬架评价指标均方根值 表6 车身垂直加速度优化幅度 1) 建立了1/4二自由度主动悬架模型,并在Simulink环境下仿真,为悬架控制方法的研究提供动力学基础。 2) 以最大程度改善车身垂直加速度目标,提出一种基于自适应差分进化算法优化单神经元PID控制的控制方法,在同一条件下使用不同控制方法分别对主动悬架进行控制仿真,对比车身垂直及速度的大小。 3) 车辆在不同载荷、不同路况下的仿真结果表明,采用自适应差分进化算法优化单神经元PID控制器,大大降低了车身垂直加速度,保证了乘客的乘坐舒适性,验证了自适应差分进化算法优化的有效性,提高了控制器的有效性和鲁棒性。






5 结论

