基于飞机性能影响的路径优化算法

回 忆，魏志强，魏路欢

（中国民航大学空中交通管理学院，天津 300300）

随着欧洲空域一体化改革的推进，空域使用规则逐渐向更加灵活机动的方向发展，使得航空公司可以更加灵活地选择各个航段，形成一条最佳航路，以降低从国内直飞欧洲航线的燃油消耗和飞行成本。

给定起点以及终点，寻找出一条可行路径的问题 在 无 人 机［1⁃2］、机 器 人［3⁃5］、游 戏 地 图［6⁃7］等 领 域 拥有广泛的应用场景，其中寻路空间模型和寻路算法问题引起了学者们的大量关注。寻路空间模型可分为几何模型和符号模型，前者的典型代表有基于栅格和基于边界的模型，主要利用各对象的坐标信息对空间进行精细划分；后者的典型代表是基于集［8⁃9］和基于图［10⁃12］的模型，主要利用各对象间的拓扑关系处理模型。处理航路问题时涉及的航路网络虽然也包含坐标信息，但它是典型的图模型，利用航路点之间的已知关系建模更加方便合理。

常见的寻路算法［2］有传统的图遍历算法，如深度优先搜索（Depth first search，DFS）、广度优先搜索（Breadth first search，BFS）、BFS 在有权图中的扩展Dijkstra 算法、在Dijkstra 算法基础上引入启发函数的A*算法；还有蚁群算法、粒子群算法、遗传算法等优化算法［13⁃15］。Dijkstra 算法可以实现从一个顶点到其他各点的最短路径，这种全局搜索在做替代方案决策时会有一定的优势［1］，但缺点是对于大规模问题可能无法在可接受的时间内给出精确的最优解。启发式A*算法则是在其基础上针对目标有方向地进行搜索，适用于大规模图中的寻路行为，其中最差的情况是将图中的边和点全部考虑到，它的关键在于找到一个合适的估值函数，在保证能得到最优解的前提下尽量提高搜索效率。

康文雄等［16］提出了基于回溯法的分层Dijkstra算法，通过分层结构寻找局部最优解来求得全局最优解或次优解，出解速度较快，数据量较大时能快速找到次优解；薛双飞等［17］在处理船舶航线规划问题时考虑到海上风电场区内船舶避碰问题，利用改进的人工势场模型分别建立风机威胁和他船威胁的势场，栅格化地图生成威胁地图，以此作为权重，利用A*算法找到优化航线。类似地，黄冬梅等［18］考虑到风浪因素对航行造成的危险，筛选出危险点集后，使用动态风浪网格数据确定权重并得到优化航线。

上述研究所涉及的图模型中的各边权重有些是固定值，有些是针对动态环境不断变化的，但这种外界的变化与寻路过程本身是不相关的，也就是说并不会因为前续路线的选择问题影响图中各边权重变化。但是，在巡航航路优化过程中，边权重（如航段油耗、成本等）与飞机在该边起始点的重量有关，而该重量值又与前续路线的实际油耗有关，也就是说不同的前续路线会造成同一条边的权重不同，因此需要在优化中实时计算边权重和估值函数。再结合计算权重时需要将航路划分成段进行重量迭代计算，每次分段后的计算都需要进行相应的飞机性能参数的积分计算与高空风温数据插值计算，这样的处理过程与传统的权重为距离常值相比，计算资源消耗较大［19］，该问题本身规模也较大，如何处理此类权重计算和寻路算法是值得研究的。首先对高空气象预报数据、航路数据、飞机性能参数计算模型进行了处理，在此基础上建立了高空航路优化算法，然后找出使寻路算法有最佳表现的A*算法估值函数系数和性能计算步长，最后针对典型飞行任务，对不同优化目标下的结果进行对比，分析了成本指数、飞机起始质量和飞行高度层等因素对航路优化的影响。

1 高空飞行航路优化算法

1.1 高空气象预报数据的处理算法

根据二进制的通用规则分布信息版本2（Gen⁃eral regularly⁃distributed information in binary form，GRIB2）格式原始气象数据［20⁃21］，提取出特定时刻下，由不同经纬度以及不同气压高度确定的网格气象数据，包括且不限于：对流层顶温度、各等压面温度、各等压面风速u方向分量和v方向分量等。其中风速是矢量，由东西方向风分量u和南北方向风分量v共同决定，其大小ws与方向wd分别为

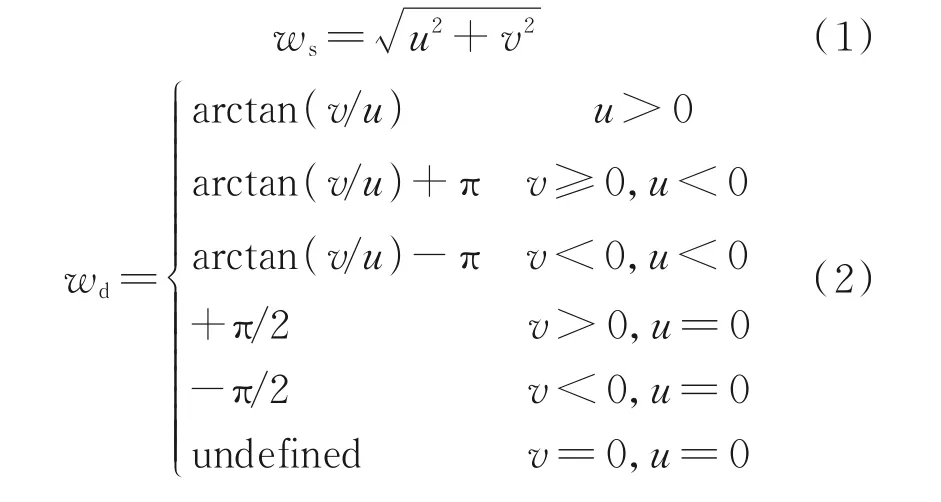
当需要考虑某段航路上的风速时，找到该航段中点，采用双线性插值法得到该中点处的风速，并用此值近似代表整段航路上的风速。该风速矢量在航向上的投影即顺（逆）风分量，直接影响地速和航行时间，是稍后的性能计算中所需的重要参数。中点温度可通过类似的方法进行计算，并用以代表整段航路上的温度。

1.2 性能参数的迭代计算方法

航油成本在民航运输中所占比重相当高，合理的飞行油耗可以有效地降低成本。在给定飞机质量、飞行高度和气象风温的条件下，燃油流量和飞行速度可根据性能数据库求出，继而飞行时间可求，而飞机油耗由燃油流量和飞行时间共同决定。但是，随着燃油的消耗，飞机质量越来越小，该参数又会对燃油流量和飞行速度的计算带来影响。所以，采取如图1 所示的迭代方法，针对研究路径内的每段航路，计算过程中将飞机质量迭代至不再发生变化为止，再据此计算该段航路上的飞行油耗和飞行时间。

图1 性能计算方法Fig.1 Algorithm of performance calculation

1.3 飞行成本计算模型

飞行成本指数可以用来衡量航班的总成本，它被定义为小时成本与燃油成本的比值，即

式中：Chr为除燃油成本外的每小时使用成本，单位元/时；Clb为每百磅燃油成本，单位元/百磅。与飞行有关的航班总成本由燃油成本和时间成本组成，即

式中：t为飞行总时间，单位小时；F为飞行燃油总消耗量，单位千克。整理可得

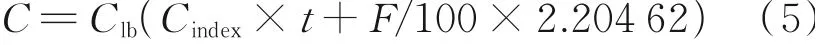
在刚刚计算飞行油耗和飞行时间的基础上，笔者可以计算出航班飞行成本C，单位元。

1.4 航路数据的加载与处理流程

使用航空无线电通信公司（Aeronautical radio incorporated，ARINC424）格式的航路数据，根据格式规则将数据文件导出整理形成csv 文件。其中每行数据代表一个航段，包括航段所属航路名、相对位置、起始航路点、终止航路点经纬度等。分析该航路数据文件，发现其中存在了一些名称相同但经纬度位置不同的航路点。故数据处理前需要进行数据检查，对重名航路点重新进行命名。具体流程如图2 所示。

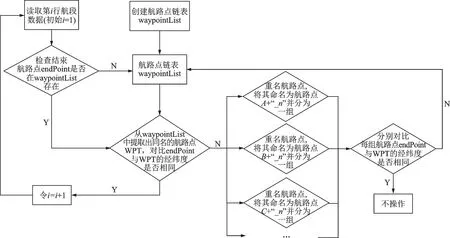
图2 重名航路点处理流程Fig.2 Process of duplicated name waypoints

1.5 航路优化算法的改进

基于已经转换成连通图的航路网络结构，不同目标下的航路优化问题可看作是基于图论的最短路径问题。该问题的一般提法如下：设G=（V，E）为连通图，图中各边（vi，vj）有权lij（lij=∞表示vi、vj间无边），va、vb为图中任意两点，求一条道路μ，使它是从va到vb的所有路中总权最小的路，即

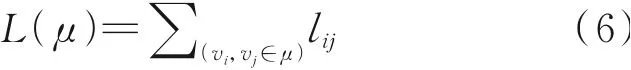
最小（考虑单源点的最短路径问题）。式中va、vb分别为航路的起点和终点，连通图G即航路网络。各边的权重根据航路优化目标的不同，可以是两航路点间的距离、飞过两航路点所需的油耗、飞行时间、飞行成本。

航路网络图中的航路点密集程度很高，在这种情况下，寻找起点和终点间的最优路线对计算量的需求相当大。考虑到制定航线的实际情况，起点和终点间的大圆航线几何距离最短，根据不同目标寻找到的最优路线会有一定程度的偏离但不会偏离过多。因此，在进行航路优化时，研究范围被缩减在以起点和终点为焦点的椭圆内，椭圆长轴的长度控制可变，通过适当选取起点和终点间距离的倍数确定（见图3），使用该图替换原航路网络图。

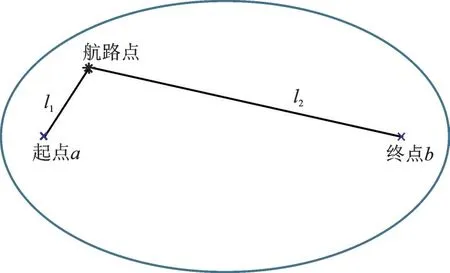
图3 航路网络计算域的椭圆形裁剪Fig.3 Ellipse cropping of the computational domain of route network

Dijkstra 算法虽然可以得到准确的最优解，但全局搜索耗时较久，此处采用启发式A*算法进行加速。A*算法中涉及的估值函数h是在考虑气象条件的情况下，基于当前点与结束点间的大圆航线对飞行油耗、时间、成本等性能进行计算，由于它本身是一种估计值，可以设计对h乘以一个系数k来表征所选估值函数的变化程度，然后选取合适的参数使得在计算代价相对较小的情况下得到满意的目标路径。

2 计算分析

前面介绍的算法部分适用于飞机性能允许范围内的任意飞机初始质量、成本指数、飞行高度值，这些参数的变化虽然直接影响优化结果，但通过大量的算例分析，发现他们的变化趋势是一致的。所以，为了使计算结果的呈现更加简洁清晰，本部分从一到两个具体的飞行任务案例出发，分析算法涉及的相关参数以及不同的优化目标（最短飞行路径mins，最少飞行油耗minF，最快飞行时间mint，最低飞行成本minC）带来的优化结果。

本部分的案例涉及的气象数据来自某航空公司2020 年5 月7 日0 时的高空气象GRIB2 文件，通过飞过航路点的经纬度位置以及飞行高度层可以确定出当地的国际标准大气（International stan⁃dard atmosphere，ISA）温度偏差。

2.1 估计代价函数系数的影响

当A*算法中估值函数h的系数k等于零时，正是Dijkstra 算法的实现步骤。因为Dijkstra 算法是可以给出准确的目标路径的，变化估值函数的系数k，在全球航路网络中选取起点ITE，终点OK，按照成本指数50、飞机起始质量295 000 kg、飞行高度层9 500 m 的计算条件，以minF为目标进行航路优化。对比优化结果、运算时间（以Dijkstra 算法得到准确解的时间为基准1，计算运算时间比值）、累计访问航路点数目，具体如表1 所示。

表1 不同估值函数系数对应的优化结果、运算时间和累计访问航路点数目Table 1 Optimization results, calculation time and cu⁃mulative number of visited waypoints for differ⁃ent estimated cost coefficients

实际上，k=0 和k=0.1 情况下得到的优化路线 是 完 全 一 致 的：ITE—SANDA—ROKKO—CUE40—TOZAN—TSUNO—JEC—BOKSA—NAMER-OK，该路线下的飞行油耗是60 124 kg；当k取其他值时，会得到稍区别于上一条优化路线的 另 一 条 路 线：IT E—S A N D A—R O K K O—C U E 4 0—T O Z A N—RAKDA—JEC—BOKSA—NAMER—OK，该路线下的飞行油耗是60 135 kg，比准确解多消耗了0.02%的燃油。与此同时，观察运算时间和累计访问航路点数目可以看到，随着k值的增加，计算开销显著减小，选取较大的k值可以在保证准确性的基础上提高计算效率，接下来的计算过程取k=0.9。

另外，涉及性能计算的质量迭代问题，原则上令计算中涉及的每段航路距离尽可能小，这样飞机质量值能够得及时更新，结果会更加准确。实际上考虑到航程距离和计算代价，选取固定的计算步长，每次计算时取该步长与它和下一航路点间的距离中的较小值作为计算步长。与前文研究估计代价函数系数对优化结果的影响类似，变化该计算步长，在全球航路网络中选取起点ITE，终点OK，按照成本指数50、飞机起始质量295 000 kg、飞行高度层9 500 m 的计算条件，以minF为目标进行航路优化。对比优化结果、运算时间（以固定步长等于20 km 时的所需运算时间为基准1，计算运算时间比值）、累计访问航路点数目，具体如表2 所示。

表2 不同固定步长对应的优化结果、运算时间和累计访问航路点数目Table 2 Optimization results, calculation time and cu⁃mulative number of visited waypoints for differ⁃ent calculation steps

实际上，表格中的3 种情况下得到的优化路线是完全一致的：ITE—SANDA—ROKKO—CUE40—TOZAN-RAKDA—JEC—BOKSA—NAMER—OK，取不同的固定步长导致最终计算得到的飞行油耗有细微区别。前面已经提到固定步长越短，质量迭代越精确，此处以20 km 固定步长所对应的运算时间作为基准，可以发现随着步长的进一步提高运算时间的减少并不明显，但计算油耗值却越来越偏离准确值，接下来的计算过程取固定步长等于100 km。

2.2 不同优化目标的结果对比

在全国航路网络中，选取起点BUNTA，终点P13，按照成本指数50、飞机起始质量255 000 kg、飞行高度层9 500 m的计算条件，分别以mins、minF、mint、minC为目标进行航路优化，结果见表3。

表3 BUNTA 至P13 不同优化目标结果对比Table 3 Comparison of results of different optimization goals from BUNTA to P13

2.3 成本指数对优化结果的影响

根据前面的优化结果可知，以minF、mint和minC为优化目标时会得到相同的航路优化结果。所以接下来选定minC和最短路径为优化目标，考虑由成本指数带来的影响，分别选取成本指数等于20、50、80 和110，按照飞机起始质量255 000 kg、飞行高度层9 500 m 的计算条件，在全国航路网络中选取起点BUNTA、终点P13 进行航路优化（见图4）。

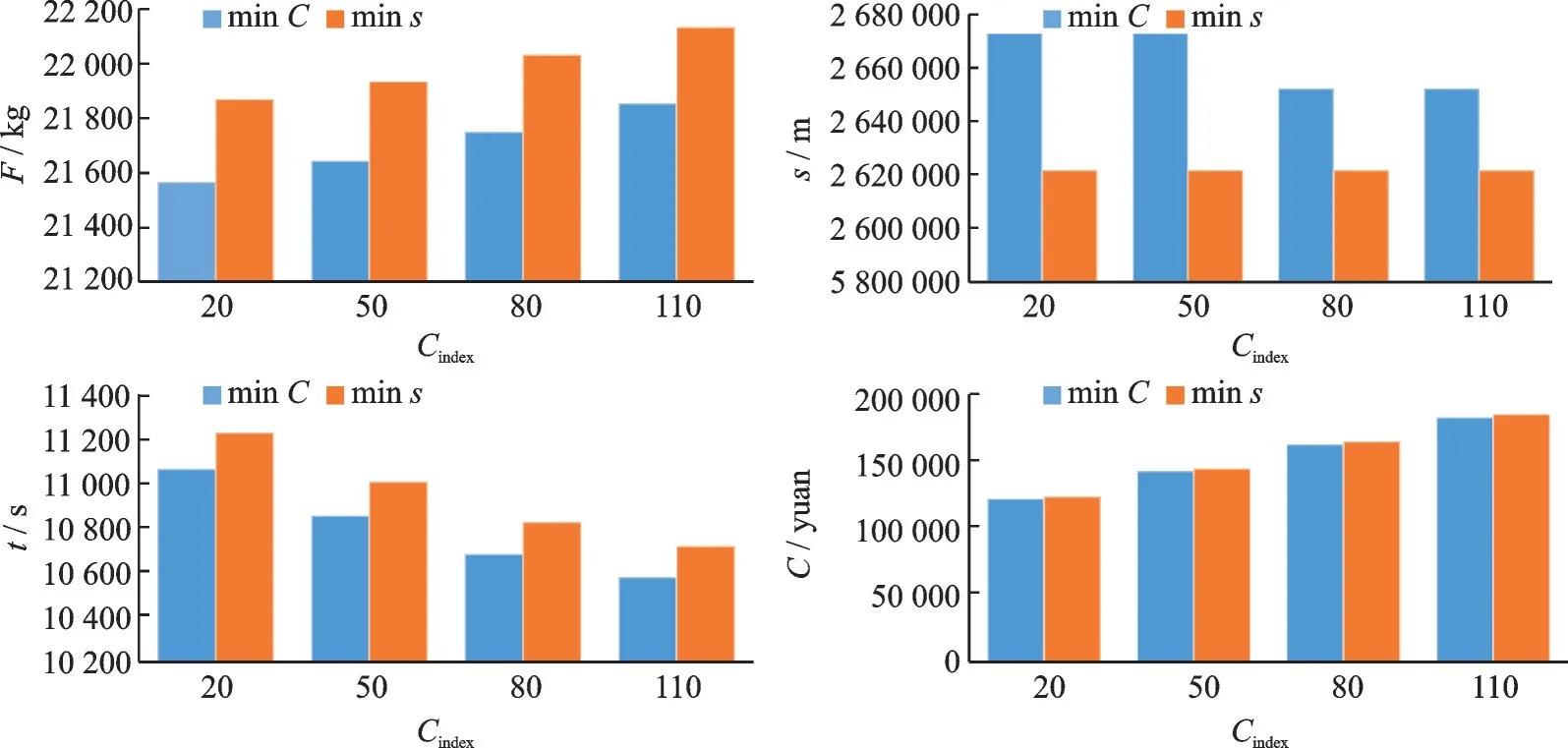
图4 不同成本指数对BUNTA 至P13(全国航路)的航路优化的影响Fig.4 Impact of different cost indices on optimization from BUNTA to P13 (national airways)

2.4 飞机质量对优化结果的影响

类似地，选定minC和最短路径为优化目标，考虑由飞机起始质量带来的影响。分别选取飞 机 起 始 质 量 等 于215 000、235 000、255 000 和275 000 kg，按照成本指数50、飞行高度层9 500 m的计算条件，在全国航路网络中选取起点BUN⁃TA、终点P13 进行航路优化（见图5）。

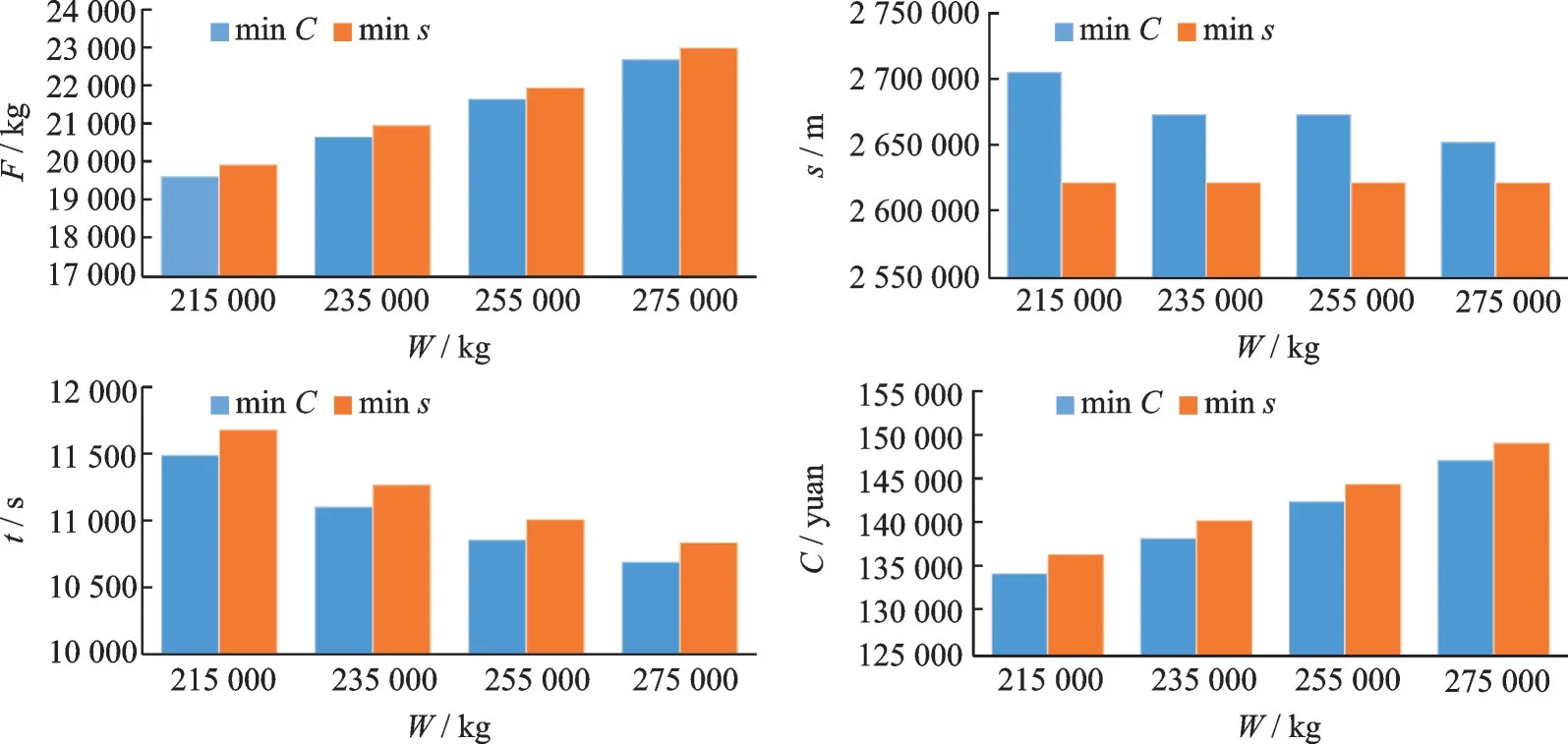
图5 不同飞机起始质量对BUNTA 至P13(全国航路)的航路优化的影响Fig.5 Impact of different aeroplane masses on optimization from BUNTA to P13 (national airways)

2.5 飞行高度层对优化结果的影响

最后，选定minC和最短路径为优化目标，考虑由飞行高度层带来的影响。分别选取飞行高度层等于8 900、9 500、10 100 和10 700 m，按照成本指数50、飞机起始质量255 000 kg 的计算条件，在全国航路网络中选取起点BUNTA、终点P13 进行航路优化（见图6）。

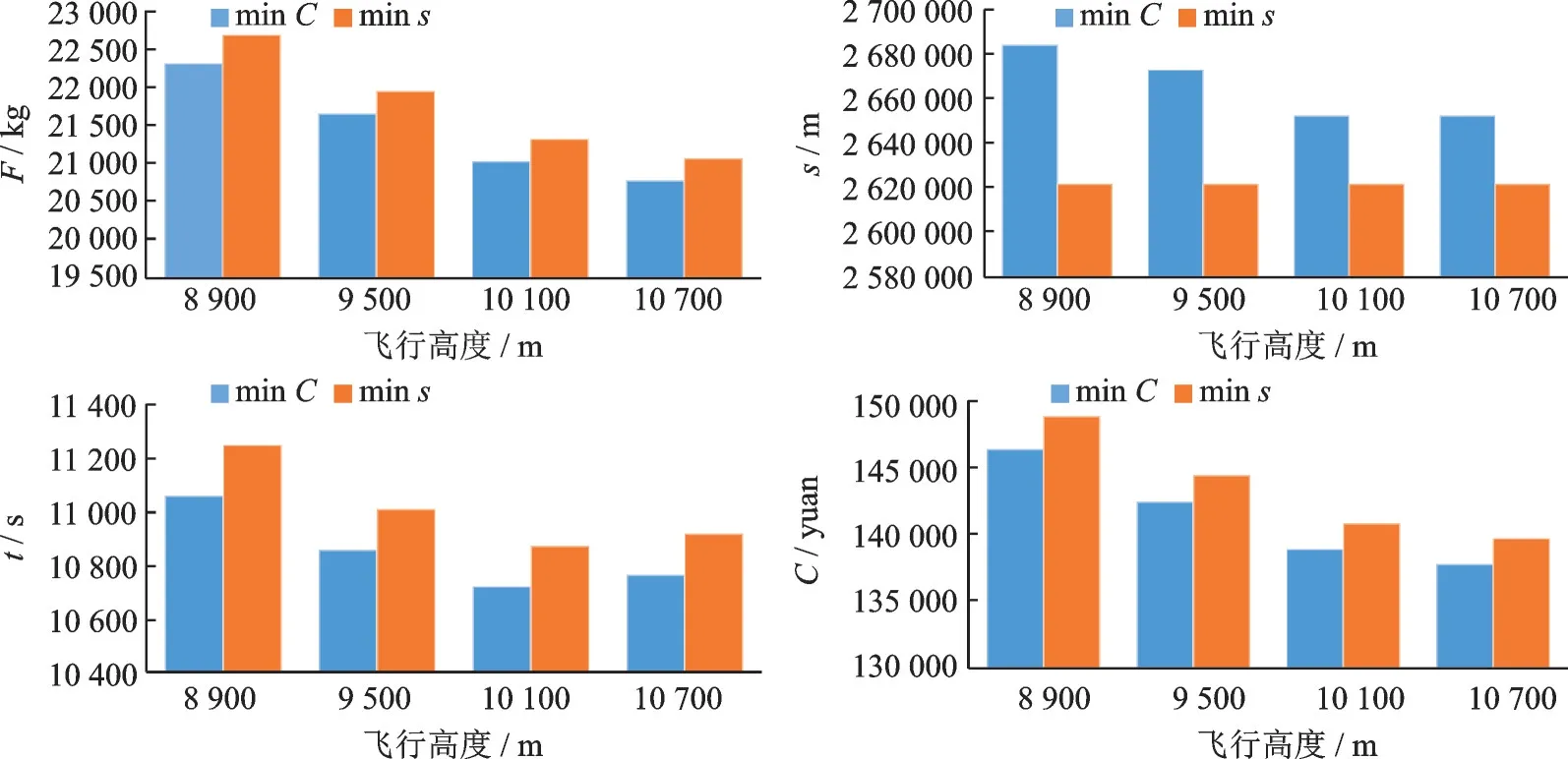
图6 不同飞行高度层对BUNTA 至P13(全国航路)的航路优化的影响Fig.6 Impact of different flight altitudes on optimization from BUNTA to P13 (national airways)

3 结 论

分别以mins、minF、mint、minC为目标进行高空巡航航路优化，讨论了经过改进的A*算法在大规模航路图中的适用性。优化目标不同，所得优化路径不一致，其中以飞行性能为目标minF、mint、minC可以得到相同的优化路线，而以传统最短路mins为目标得到的优化路线是不同于其他情况的，此结果与预期相符，一方面改进A*算法相对于传统最短路算法会增加计算时间，另一方面同样以飞行性能最优为目标的情况下，相较于Dijkstra 算法它可以更迅速地找到优化路线。

成本指数不同决定优化路线时，是燃油成本的影响更大还是时间成本的影响更大，在相同的某种优化目标下，对于得到的优化路线，成本指数越高，油价影响越小，飞行油耗越高，时间影响越大，飞行时间越短；而飞机起始质量越大、飞行高度层越低时，飞行油耗越高。可以看出，以飞机性能和气象数据为基础的航路优化算法的影响因素较多，最低成本优化结果与传统最短路径优化相比，可减少燃油消耗，减少飞行时间，降低成本，产生不错的经济效益。

由于各地区实际运行情况并不相同，本文的研究内容没有涉及当地的相关运行规则以及实际可能会碰到的相关管制情况，而是选择使用了单一简单图模型来作为研究基准对象，目的是为了保证算法的普适性。后续可根据研究的具体区域在该基准模型的框架下进行相应的限制修改，为后续研究服务。