刍议初中学生几何语言表达能力培养的路径

孙延军

山东省滨州市博兴县第六中学 256500

初一几何教学的重点是要解决学生入门学习的问题.新课标提出，七年级学生要理解与掌握直线与角、相交线与平行线等知识.虽然这部分知识是最基础的几何知识，但正因为它的基础性，却成了初一几何教学的难点.为什么基础的几何知识却成了教学的难点呢？其主要原因在于学生刚开始接触几何语言，未能很好地掌握几何语言，由此可见几何语 言的重要性［1］.如何教 会学生掌握几何语言，笔者以为，提高学生几何语言表达能力是一条有效的路径.基于理论研究与教学实践，笔者通过案例的形式，阐述培养学生几何语言表达能力的路径.

在图形性质的教学中，培养学生几何语言表达能力

在几何教学中，不少教师认为讲得足够详细，思路足够清晰，学生就一定能理解接受并进行正确书写.事实并非如此，由于部分学生几何语言表达能力的缺乏，导致他们不会书写解题过程，更不会运用几何语言分析解决问题.因此，培养学生几何语言表达能力的训练尤为重要.具体教学中，教师可以分三个步骤进行：一是教师设置合理的问题，在学生逐步回答问题的过程中理清解决问题的思路；二是让学生口头表达解题过程，在学生一边说的过程中，教师一边纠正；三是让学生到黑板上板书解题过程.

例1“角平分线性质应用”教学节选

如图1所示，射线OC在∠AOB的内部，OM，ON分别是∠AOB，∠AOC的平分线.

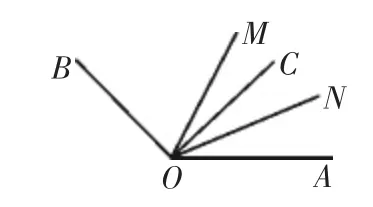
图1

（1）如果∠AOB＝140°，∠AOC＝60°，那么∠MON是多少度？

（2）请写出∠MON与∠BOC的数量关系，并说明理由.

师：什么是角平分线？已知角平分线，可以得到什么结论？

生：在角的内部，如果一条射线把一个角分成两个相等的角，那么这条射线就是角平分线.通过已知角平分线，可以得到相等的角，可以得到角的2倍关系或一半关系.

师：由“射线OC在∠AOB的内部，OM，ON 分别是∠AOB，∠AOC 的平分线”，可以得到什么结论？

生：由“OM是∠AOB的平分线”可以得到∠AOM＝∠BOM，∠AOM＝∠BOM＝∠AOB，∠AOB＝2∠AOM＝2∠BOM.同理，由“ON是∠AOC的平分线”，可以得到∠AON＝∠CON，∠AOC＝2∠AON＝2∠CON.

师：由“∠AOB＝140°，∠AOC＝60°”，你可以得到什么数值？

生：由“∠AOB＝140°”，可以得到∠AOM＝∠BOM＝70°，由“∠AOC＝60°”，可以得到∠AON＝∠CON＝30°.

师：所求∠MON与上述哪些角有关？它的角度如何求得？

生：从图上可以看出，∠MON ＝∠AOM－∠AON，把∠AOM＝∠BOM＝70°，∠AON＝∠CON＝30°代入，得∠MON＝70°－30°＝40°.

师：∠MON与∠BOC的数量关系是什么？为什么？

师：请同学们复述解题过程.（抽3名学生到黑板上书写解答过程）

教学中，采用师生问答的形式，由角平分线的定义入手，由一般到具体，再由具体到一般，在回答问题的过程中，学生自然说出解题思路，凸显了学生的主体地位以及教师的指导作用.在学生自行复述解答过程时，实现了生生互动，学生敢于开口，愿意开口.学生在板书解答过程时，暴露了思维的缺陷，笔者对症下药，帮助学生养成认真书写的习惯.

在证明过程的教学中，培养学生几何语言表达能力

在三角形的判定定理中，出现了“边边边”“边角边”“角边角”“角角边”等几何术语，简单的三个字包含了判定三角形全等的条件，但是学生要理解它们的含义，明确它们的条件还有一定的困难，比如有些学生常把“边角边”与“边边角”混为一谈，把“角边角”与“角角边”混为一谈.教学中，教师应引导学生明白分别对应相等的含义，在步步说理中培养学生的几何语言能力.

例2“全等三角形判定定理的应用”教学节选

如图2所示，点E，F在AB上，且AE=BF，DE=CF，CF∥DE.求证：AC∥BD.

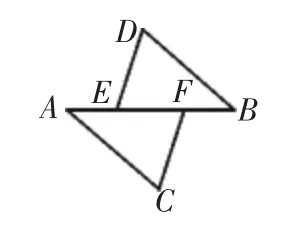
图2

师：在图2所示的图形中，如何证明AC∥BD？为什么？

生：根据内错角相等，两直线平行，当∠A=∠B时，AC∥BD.

师：∠A，∠B 分别在哪个三角形中？这两个三角形能直接证明全等吗？为什么？

生：∠A，∠B分别在△ACF与△BDE中，这两个三角形不能直接证明全等，因为AE，BF不是△ACF，△BDE的对应边，对应边DE，CF相等且平行，没有对应角相等的条件.

生：由“AE=BF”可得“AE+EF=BF+EF”，即AF=BE，由“CF∥DE”，根据两直线平行，内错角相等，得∠DEB=∠CFA.又因为DE=CF，根据两边分别对应相等，且夹角相等的的两个三角形全等，得△ACF≌△BDE.根据全等三角形对应角相等，得∠A=∠B，再根据内错角相等，两直线平行，得AC∥BD.

师：请同学们复述上述证明过程，请一位同学板演.

教学中，从所求证的结论出发，寻求使结论成立的条件，采用倒追的形式，比如AC∥BD→∠A=∠B→△ACF≌△BDE→AF=BE，∠DEB=∠CFA→AE=BF，CF∥DE.学生明确了解题思路，然后运用综合法书写解题步骤，为后期学生解答与全等三角形的性质与判定有关的问题做好了铺垫.

在图形变换的教学中，培养学生几何语言表达能力

初中阶段学习的图形变换有四种，其中轴对称、平移与旋转属于全等变换，图形只是在位置方面发生变化，图形的大小与形状并没有发生变化，相应地对应角与对应线段也没有发生变化，这些都是全等变换的共性，那么，它们的特性是什么？虽然学生能从直观上加以区分，但要掌握各种变换的概念、变换的性质与作图方法，学生很难做出准确的描述.在实际教学中，教师可以让学生通过大量的口头训练，帮助学生抓住其中的关键词，通过关键词掌握各种变换方式的描述.

例3“关于图形变换的应用”教学节选

如图3所示，试说明△A′B′C′是由△ABC通过怎样的图形变换或变换组合（平移、旋转、轴对称）得到的？

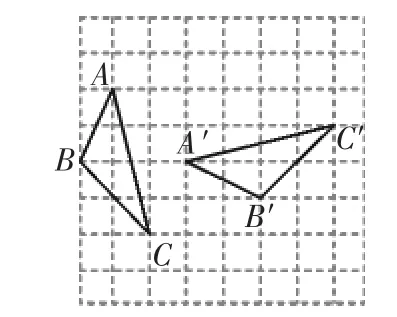
图3

师：从△ABC到△A′B′C′，经过了哪些图形变换？

生：从△ABC变换到△A′B′C′，经过了旋转变换与平移变换.

师：在旋转变换中，它的决定要素是什么？对于本图又是如何旋转变换的？

生：旋转变换的决定要素是旋转中心，旋转方向与旋转角度，对于△ABC与△A′B′C′，以点B为旋转中心，旋转方向是逆时针，旋转角度是90度.也就是说让△ABC先绕点B逆时针旋转90度.

师：在平移变换中，它的决定要素是什么？对于本图又是如何平移变换的？

生：平移变换的决定要素是平移的方向与平移的距离.对于△ABC与△A′B′C′，平移方向是先向下再向右，平移的距离分别是1格与5格.也就是说，△ABC经旋转变换后的图形，先向下平移1格，再向右平移5格.

师：请同学们用“先如何变换再如何变换”的形式，描述整个变换过程.

生：先将△ABC绕点B逆时针旋转90度，再将△ABC经旋转变换后的图形，先向下平移1格，再向右平移5格.可得△A′B′C′.

通过观察图形，从△ABC到△A′B′C′，需要经过旋转与平移两种变换，但是如何详细地描述这两种变换，把变换的过程说明白，需要教师多加引导.笔者通过抓住两种变换的关键词，如旋转变换抓旋转中心、旋转方向与旋转角度，平移抓平移方向与平移距离，使学生很顺利地描述了这两种变换.不难发现，当学生能够准确把握变换特征描述变换过程时，思路会比较清晰，语言会比较流畅.

在平面几何里，有许多特殊的语言工具，如平行与垂直、互余与互补、全等与相似、平移与轴对称、旋转与中心对称等.在每一道习题的解答过程中，都需要用它们来进行描述，实际上语言能力培养说是前提，写是结果.心理学家赫瑞特拉指出，当一个人阅读时可以记住50%，听别人讲话时可以记住20%，观察时可以记住30%，当与他人交流时，可以记住自己所讲内容的70%［2］.因此，培养学生几何语言能力，必须让学生多进行口头练习，在说的过程中体会几何语言，在说的过程中把握几何语言的严谨性，进而提高学生的几何语言表达能力.