指向素养培育的初中数学深度学习的教学策略
闫希美
山东省滨州市滨城区第三中学 256600
在实际的数学教学中,常常会有这样的教学场景:课堂上教师致力于讲解示范,“自导自演”着教与学的过程;学生不是完成概念与公式的死记硬背,就是进行练习题的模仿性练习.在这样的教学过程中,学生的成绩也能在短期内小见成效,但这种缺乏主动学习和深刻学习的方式,使得学生的思维“停滞不前”,稍有变式的问题都能令其“裹足不前”,显然不利于学生数学素养的培养.
深度学习作为一种全新学习理念和学习方式,是指学生在理解学习的基础上,深层加工知识,以获得对数学知识的深度理解、自主建构和长期保持.对初中数学教学而言,深度学习就是搭建数学知识与学生思维的桥梁,是一种指向能力和素养的学习方式.笔者认为,将指向素养培育的深度学习落实到现实的课堂教学中,可以实施以下具体的教学策略.
营造和谐氛围,为学生深度学习赋予生命成长的力量
深度学习是一种积极主动的学习过程,并非被动的识记或单纯的理解过程.那么以民主、宽松、和谐的学习氛围取代传统教学中的师道尊严,便是开展深度学习的第一步.因此,教师需用真情点燃学生的热情,有效营造和谐宽松的学习氛围,为学生深度学习赋予生命成长的力量.
(一)平等共享的师生关系
一直以来,人们信奉“亲其师、信其道”的教学理念,现代教学观也同样遵循这一教学理念.然而想要学生真正亲近教师和相信教师,就需要在平等宽松的氛围中,教师以“学业指导”的身份引领学生去发现、探索和建构,整个过程中师生间敞开心扉,相互沟通、吸纳、互动、交流,唯有如此,才能达到构建平等共享师生关系的目的.
在这样的课堂氛围中,教师需尊重、宽容、爱护和善待每个学生,想方设法地通过有效策略唤起学生的学习兴趣,细致入微地激励学生的自主意识,深入浅出地激发学生的创造力.这样才能为学生的探索、合作、交流打开一扇窗,才能让深度学习的课堂源源不断地流淌学生生命成长的源泉.
(二)激励成长的课堂评价
深度学习可以帮助学生建构具有迁移性的知识图谱,是一种高投入、高认知和高产出的学习方式.深度学习下的课堂评价不仅要关注学生知识技能的获取,还要关注学生的情感态度与价值观.初中生的心智尚未成熟,他们的深度学习必然是建立在教师的支持之上,鉴于课堂评价的促进效能,所以教师需要通过激励成长的课堂评价这条明线来服务于学生的“学”,为学生的深度学习搭建“脚手架”,让学生的学习充满生命活力.
案例1一元二次方程
问题:关于x 的一元二次方程x2+(2k+1)x+k2-2=0的两根的平方和等于11,试求k.
师:请两名学生上讲台板演.
学生跃跃欲试,很快两名学生完成了板演.果不其然,由于初学且不够深入,所以两名学生均得出了错误结果k1=1,k2=-3.
师:非常好,你们都娴熟地运用了根与系数的关系来解决本题,这一点值得表扬,不过结果却有一点错误,错在哪里呢,为什么错呢?
学生开始陷入思考,并小声讨论.
师(点拨):我们先来思考一下几个问题,看看能不能找到一点思路:
问题1:x2-2x+2=0可有实根?
问题2:“x2-2x+2=0 的两根之和是2”这个说法对吗?为什么?
问题3:回到之前的问题,现在你想到了什么?有没有什么遗漏了呢?
由于有了问题的指引,学生的分析、探索和讨论有了明确的方向,片刻之后,学生有了想法和发现.
生1:我知道了,我遗漏了Δ≥0这个重要的前提条件……
在推进深度学习的策略中,课堂评价是时常被忽略的重要一环.事实上,作为可以促成生成的课堂评价,自然能对学生深度学习产生推进作用.本例中,合理的课堂评价发挥了推进作用,促成了学生知识、思想、能力等方面的生成与发展.更重要的是,有了对Δ≥0本质的追问,使得学生在今后解决此类问题时有了“警戒线”,自然可以避免此类错误的发生.
指导自我提问,以问题提升学生深度学习的效度
所谓“自我提问”,就是自问自答的一种学习方式,在问与答之间可以帮助学生理清思维过程,拓展思维的宽广度,最终实现深度学习和自主学习.当然,学生的自我提问能力并非与生俱来,需要教师发挥榜样效能,时时示范提问方法,尽可能站在学生的角度去提问.就这样,教师常常进行合理而适切的指导,让学生感知思维浅入深出的过程,自然获得自我提问的技能,提升深度学习的效度.
案例2有序数对
问题1:请利用数学结合文字来描述你家的位置.
问题2:下周我们班要开家长会,你能利用数对来告知家长自己在教室的位置吗?
问题3:你能类比以上问题,提出一个用有序数对表示物体位置的问题吗?
学生想要学会提问,首先需要“得道”,再者就是需要时常“历练”,只有将其变为习惯才是真正拥有了这个能力.以上案例中,教师牢牢抓住机会,引导学生质疑问难,引导学生的思维走向深处,让课堂充满生机与活力,这才是深度学习课堂该有的样态.
组织延伸拓展,促成学生开放的知识结构
把握知识探索的延伸点进行延伸拓展,可以让学生的探究兴趣持续下去,有效拓展学生的思维空间,这也是深度学习课堂的魅力之处.因此,教师在教学中需要通过变式、发散和拓展的方式,让问题具有开放性、挑战性和拓展性,进而拓展学生对数学知识的认知深度与广度,促进学生的思维之树茁壮成长,自然形成开放的知识结构.
案例3如图1,已知∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别与AB,AC交于点D和E.证明:BD+CE=DE.

图1
在学生完成之后,教师调整原题,引入以下变式:
变式:如图2,已知等腰ΔABC中,有AB=AC,且∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC,分别与AB,AC交于点D和E.请在观察后找出图中所有的等腰三角形.
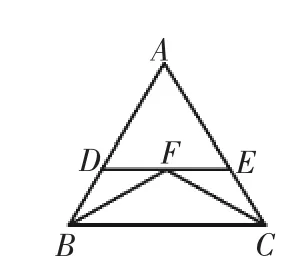
图2
生1:共有△ADE,△EFC,△BFC,△BFD4个.
师:在探索中,你们还有其他发现吗?
这一创造性问题让思维活跃的学生有了各种生成.
生2:据CE=EF,BD=DF,可得DE=BD+CE.
生3:继续生2 的推导,可以得出△ADE的周长=AB+AC.
生4:据F到△ABC的三边距离相等,可知AF为∠BAC的平分线.
师:你们真是思维敏捷的孩子,一下子得出如此多的结论.那么,现在去掉原题条件中的“等腰”和“AB=AC”,还能得出上述结论吗?(学生又一次陷入思考)
生6:只剩下△EFC和△BFD两个等腰三角形了.
生7:其余结论仍然成立.(学生又七嘴八舌地进行了证明)
师:哇,你们独立探索的能力已经超出了老师的想象.根据“点F为∠ABC与∠ACB的平分线的交点”,你们想到了什么?(大部分学生沉思,个别学生有了些许领悟)
生8:这里是内角平分线,应该可以想到外角平分线.
其他学生在该生的启发下,自主自发地展开了探索和讨论,将课堂推向深处.
……
以上案例中,教师从原题出发,通过变式拓展让问题的探究性和思维性更加强烈,使得学生在深入探究之余不禁“流连忘返”.显然在这样的思维碰撞中,学生水到渠成地有了“点F还可是∠ABC的内角平分线和∠ACB外角平分线的交点”这一创造性发现,形成了自己开放的知识结构,很好地培养了数学核心素养.
总之,指向素养培育的深度学习,需要营造平等和谐氛围,为学生深度学习赋予生命成长的力量;需要指导学生提问,以问题提升学生深度学习的效度;需要延伸拓展的变式问题,促成学生开放的知识结构……就这样,随着学习的推进,学生经历思考、探索、讨论、抽象等思维过程,将数学知识技能、数学思想方法自然内化为自身的思维品质,在此基础上使自身的数学核心素养得到了锻炼和发展.

