重视数学严谨性 理解数学本质

陆芸婷

江苏省南通市通州区川港中学 226314

数学结论的由来都需要进行论证，特别是几何部分的内容，强调了证明的必要性，反映出数学学科具有严谨性的特点.为了帮助学生更好地理解数学内容，教材会从具体的情境和基本事实导入，以符合学生的认知特点和知识结构水平，帮助学生更好地进入学习的状态，更快速地理解这一内容.这些基本的生活情境可以使学生更加直观地感受几何图形的变化，使数学从抽象到具象，帮助学生建立起立体几何的认识，降低了学习的难度，但是给数学的严谨性也带来了冲突［1］.因 此，教师在教学时应该注意数学的严谨性.笔者从具体的教学案例出发，谈一谈如何更好地体现数学教学的严谨性.

课标与教材分析

义务教育阶段学生需要掌握几何的基础知识，主要包括：两点确定一条直线；两点之间线段最短的特点；直线垂直的定义；平行线的判定和平行线的相关性质；根据角的性质、边的相等的特点判定全等三角形；直线被平行线所截，对应线段成比例.这七条基本的数学定义，是学生必须掌握的基础知识.数学的三段论和推理规则，从原有的知识推导出结论，进而形成新的逻辑和推理方法，这是研究数学的核心原则.数学的定理都需要通过基本的假设和理论进行推导，除了不证自明的定理，其他的事物由来都需要通过基本的假设进行证明.

在各种科学领域当中，有一些不证自明的假设，这些假设被称为“公理”.在科学领域当中，还有一些没有经过验证但被大家所接受的附加的假设，这些假设被称为 “公设”.公理存在于各个科学的分支当中，不同的科学分支所具有的假设不尽相同，因此各个科学分支的公设是不同的.公设所具有的作用是在于在现实世界的经验当中，如果公设被大家所怀疑，那么就无法传递科学知识.

数学著作《几何原本》将人们根据经验总结出来的几何常识进行了很好的描述，这被称为公设.同时一些不证自明的理论在书中进行了确定，这些被称为 “公理”.随着结构主义数学的发展，人们对于公理和公设的研究进一步深化，两者之间的差异也逐渐消失了.因此一般的公设可以推导出大量的几何事实和几何定理，平面几何中的定理都可以通过这一公设进行推理而被创造出来.因此当人们改变作为基础的公设就会得到许多不同的公理和很多的理论，而这样的理论是建立在公设基础上的，故而公设不能被作为基于经验的事实，而只能是单纯的形式陈述.随着现代科学的发展，人们对于公理的认识还在不断发生变化.

基于这样的认识，教材中对于具体场景的描述就是公理的一种具体的表现方式.而教材是将这些当作不证自明的公理来对待.从长期来说，这很容易给学生造成认知误区，缺少了数学的严谨性.

公理化

几何部分的学习是从几何概念和几何定理出发，建立起逻辑体系和方法，因此可以分解成以下四个方面：①列举基础的概念；②描述基本的定义；③列举基础公理；④叙述定理和进行证明.这四个部分具有内在的联系，相互交织、相互依赖地组成在一起，四个部分按照逻辑原则相互联系和演绎，构成了公理化的体系.公理化的演绎方法是一个统一的体系，这个体系是由抽象内容和逻辑体系构成.逻辑体系的构成需要不同的概念和公理，如果公理不同，那么形成的几何体系自然也不一样.几何的逻辑结构具有不同的逻辑顺序，这主要是由公理的先后次序决定；同样的几何体系也可以呈现出不同的逻辑结构，这主要是由公理的编排次序决定.如学生在中学几何平行公理学完之后，会继续学习外角定理和三角形全等的“角角边”定理，这样就可以根据已经学过的平行公理来继续推导出“三角形的内角和等于180°”的定理，新的定理很容易获得证明.但是在欧氏几何的体系中，公理的顺序却不相同，平行公理的学习在这两个定理的后面，所以学生就不能使用“三角形的内角和”定理，再加上同一个几何问题有不同的逻辑结构，所以几何证明的方法是不同的，它在不同的逻辑结构中使用的方法和次序都是不同的［2］.这就要求 学生在进行几何证明时选择准确的逻辑体系和验证方法，如果出现方法和体系的不对称，那势必就会出现证明错误.

必要阐释的“基本事实”

为了使全等三角形的判定证明过程更易于被学生接受，符合学生的认知习惯和特点，教材的教学目标中将所有的不定义概念和所有的公理都删减了，也没有将全等三角形的三种判定方法作为一种研究的定理，而是作为“基本事实”进行讲解和提出.这实际上是为了使教学更加生动，接近学生的实际认知水平，这是几何体系中对公理的一种教学上的处理.作为定理在教材中的出现，体现了教材编写中出于严谨性的要求，但是从学生接受的程度上来说，又采取了另外一种处理的方法.那么在教学中教师应该如何处理呢？为了让学生能够体会数学的严谨性，教师是否可以通过准备材料进行证明呢？让学生通过教师的呈现了解这三条定理由于难度过大，而被当作了一个 “基本事实”，对于证明的内容和证明方法可以在教学中弱化，但是通过证明这一环节，学生会对这一“基本事实”的认识更加深刻.

数学家根据著名的第五条公设提出的等价公理：过直线外一点有且只有一条直线与这条直线平行，这条定理也简称为 “平行公理”.第五条公设的内容是这样的：如图1，如果一条直线与两条直线相交，在同一侧的内角和比两个直角小，那么这两条直线在各自不断地延伸之后，会在内角和小于两直角的一侧相交.

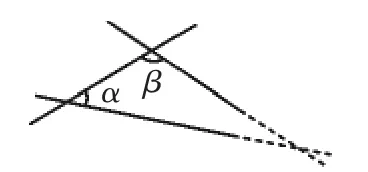
图1

经过观察学生发现，这条公设的内容和他们已经学习过的“同旁内角互补，两条直线平行”的平行线判定方法是一致的.因此这个判定方法作为一种“基本事实”相较于定理而言更易于学生接受.而“同位角相等，两条直线平行”的定理作为基本事实则不太合适，这个定理可以通过同旁内角互补的公理进行推理得出，更能体现数学的严谨和科学.因此教师在进行教材处理时要仔细斟酌，具体情况具体分析，不能“一刀切”，要从数学学科的特点和学生的发展两个角度综合考虑.从数学史发展的过程中可以看出，平行公理与同旁内角互补，两直线平行的定理可以相互替代，可以说是等价公理.因此不需要将同旁内角互补判定直线平行作为基本事实.综上所述，同位角相等判定两直线平行的方法应该作为定理进行学习，而平行公理则可作为“基本事实”.

避免采用“基本事实”说话

教材在很多地方将公理当作了基本事实，这是基于学生的认知特点和认知规律，符合教学的实际情况，但是教师不能在教学中忽视数学学科的严谨性.数学定理和结论的得到都是通过实际的观察和测量得出来的，如几何中三角形的全等、图形的平移、旋转等性质，这些虽然没有进行严格的证明，但是这些可以无须深究.当然也有一些结论的得到是例外，如证明对顶角相等的性质时，通过邻补角进行证明，这样的例子并不罕见，笔者不一一赘述.教材的编写追求数学的严谨性，在很多地方得到了体现.

如“过一点有且只有一条直线与已知直线垂直”这个结论的由来，教材没有从“基本事实”进行表述，而是通过证明得到定理.教材在课后设计了一道习题进行证明方法的渗透，证明方法也设计在初中生的能力接受范围之内，目的是希望学生将其作为定理进行学习.笔者认为在讲授这个定理时可以通过这道习题讲解证明结论的由来过程，让学生体会数学逻辑的严谨性.

对于不在同一条直线上的三个点确定一个圆的结论，教材中则采用了反向证明法，通过这一方法还同时解决了一个经常应用但是没有经过证明的结论——两条直线平行，同位角相等.严谨性是数学学科的重要特征，因此在教学过程中教师要注意对定理的由来进行证明，若是有些结论以目前学生的能力还不能证明，也要讲解清楚，不是不需要证明，是暂时还不适合进行这样难度的验证.等到进一步学习数学，掌握了更加高深的知识，学生就可以体会到数学的本质内涵［3］.

在论述结论为什么需要证明时，教材中进行了充分的描述，数学命题的正确与否需要经过有力的论证，经由充足的理论推理让人信服，才能发现观察分析、实验结论等证明的重要途径，而证明是验证数学定理和公式的必经步骤.这就传递给学生一个重要的精神，数学需要严谨的精神，而不能都通过基本事实描述.

教学反思

（一）注重数学史知识融入课堂教学

数学史是数学从产生到发展的过程，从数学史的学习中学生可以更加深入地了解这一知识产生的缘由和影响，从而在探究过程中能够吸取前人的经验，避免走前人走过的弯路，遵循历史发展的规律，促进数学成果的扩大.学习数学史的发展过程可以让学生领会前人的研究思想和方法，为课堂教学寻找新的研究路径开拓思路，也能让学生感受数学成果的得到需要经过不断的努力和探究.数学学科的发展是一个长期坚持的过程，不是一蹴而就地突然出现，是在不断地研究观察、反复实践和思考分析中逐渐完善，研究的过程复杂而艰辛，需要巨大的努力和坚强的意志，数学史的学习显然会让学生深刻感悟数学家的思维过程，更好地感受教材的本质，理解数学家严谨的态度和追求真理的精神，进而不断学习，形成正确的情感态度与价值观.

（二）渗透数学论证思想

数学中的每一个结论和定理都不能想当然，都需要通过论证，而每一步论证过程都必须有充分的依据和理由.在证明过程中的理由只能有以下几种假设：依据不证自明的公理，根据已经证明过的定理，根据理论的定义，根据证明过程中的上一步骤，根据某条逻辑准则.因此在数学学科的学习中，无论是哪一个板块，都需要通过证明.比如垂线的性质、平行线的判定、全等三角形的判定等都需要通过论证向学生进行讲授，不能当作固有的事实进行灌输，否则就忽视了数学学科的严谨性，学生的学习方式就变成了记忆，思维能力没有得到相应的发展.

（三）完善知识结构，构建逻辑体系

证明的过程一定是完整和严谨的，论证有条理有依据，过程理由充分，在一个完整的逻辑体系当中.只有证明过程严谨才能引导学生正确论证，避免逻辑错误.学生在几何论证时，容易因为所学内容的顺序造成证明过程错误，如将没有得到证明的定理用于证明未知的结论，混淆“已学”与“已证”，或者将还没有学习过的定理用于前面结论的证明，混淆逻辑顺序.因此在教学环节中，教师需要充分理解教材的编排结构和学生的认知结构与认知水平，将学生的所学内容进行有序梳理，完整恰当地安排，形成严密的逻辑顺序.

学生提取信息的过程与记忆中形成的信息痕迹和提取的线索有着很大的关系，因此教师在教学中梳理整合学生所学的内容，可以帮助学生形成比较严密的逻辑思维习惯.

综上所述，数学教学过程中教师要关注教学的严谨性，从学生思维习惯出发进行定理的证明和论证，不能将定理当作基本事实处理，在论证的过程中不断渗透严谨的学科精神，发展学生的思维能力.