复杂时变环境高速开关阀自适应控制算法

毛景禄， 王 聪， 张彦伟， 苗 峰， 崔 雷

(中车青岛四方车辆研究所有限公司， 山东青岛 266031)

引言

液压制动系统功率密度大、设备小、节约空间，制动效果平稳、快速、准确，在轨道车辆领域的应用越来越广泛[1-2]，已经成为轨道车辆制动技术的重点发展方向。目前液压制动系统主要采用比例减压阀或高速开关阀作为充液阀与排液阀，相较于比例减压阀，高速开关阀抗污能力强[3]，制动力控制精度高，能够满足恶劣工作环境与高精度制动力控制的需求，已成为目前液压制动的主流研究方向[4]。

高速开关阀开关动作主要采用PWM控制方式[5-6]，王伟玮等[7]、王东良等[8]与梁光成等[9]通过研究发现在高频PWM工作时， 通过控制方法调整合适占空比，高速开关阀的球阀可以在某一位置悬浮，通过改变占空比的大小可以改变悬浮位置，即具有比例阀的功能，但此方法对硬件设计要求较高，实际应用难度大。低频PWM波PID控制[10]是目前高速开关阀的主流控制方法，然而固定的PID参数很难适应复杂的时变环境要求。

吴昌文等[11]提出基于气动的模糊PID自适应控制，相较于气动，复杂时变液压环境下的模糊规则设计困难，当设计的模糊规则准确性较差时，将严重影响其控制精度。

为实现高速开关阀在复杂时变环境下的稳定工作需求，本研究设计提出高速开关阀自适应控制算法，在保证制动力控制精度的前提下，满足制动系统复杂时变工作环境下的自适应性和鲁棒性的控制需求。

1 液压制动原理

以主动式液压制动系统为例，其工作状态主要包括蓄能器压力供给状态、制动及缓解状态、安全制动状态和辅助缓解状态，液压原理如图1所示。

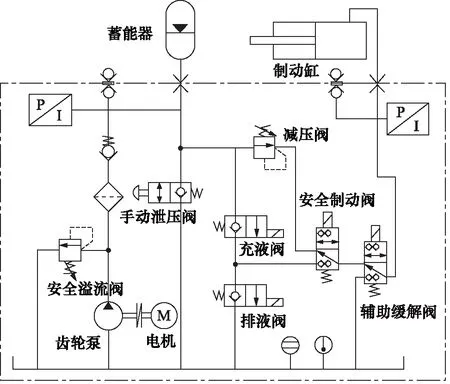
图1 液压原理图Fig.1 Hydraulic schematic

1) 蓄能器压力供给状态

蓄能器内部压力低于设定压力区间下限时，电机启动带动齿轮泵工作，蓄能器充液打压，进入蓄能器压力供给状态；蓄能器压力达到设定压力区间上限时，关闭电机，退出蓄能器压力供给状态。单向阀可使蓄能器压力手动降至0 MPa；安全溢流阀可使蓄能器充液过程中，其压力不超过系统预设安全压力值，从而保证蓄能器充液回路安全稳定运行。

2) 制动及缓解状态

在制动系统正常制动施加或缓解时，进入制动及缓解状态，安全制动阀通电，辅助缓解阀断电，根据实际制动力需求，调整充液阀与排液阀的PWM占空比，控制充液阀与排液阀的通电/断电状态，从而使制动缸压力与需求值匹配。

3) 安全制动状态

当激活安全制动指令，进入安全制动状态时，安全制动阀断电，辅助缓解阀断电，打开安全制动回路。制动缸压力通过减压阀调整到力预设值，施加安全制动力。若减压阀出现故障，则进入制动及缓解状态，通过调整充液阀与排液阀的PWM占空比，施加安全制动力。

4) 辅助缓解状态

若充液阀与排液阀出现故障，夹钳无法正常缓解时，进入辅助缓解状态，辅助缓解阀通电，制动缸中油液流入油箱，压力降至0 MPa，夹钳缓解。

2 高速开关阀

2.1 工作原理

高速开关阀结构如图2所示，电磁铁通电时，衔铁吸合，阀芯在顶杆作用下向左运动，A口与B口连通，高速开关阀处于开启状态；电磁铁断电时，衔铁在复位弹簧作用下快速脱开，阀芯主弹簧作用下复位向右运动，A口与B口断开，高速开关阀处于关闭状态。

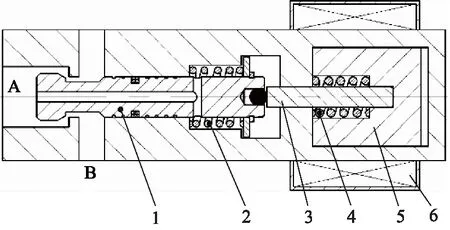
1.阀芯 2.主弹簧 3.顶杆 4.复位弹簧 5.衔铁 6.线圈图2 高速开关阀结构Fig.2 Structure of high-speed on-off valve

2.2 高速开关阀数学建模

励磁线圈电路方程为：

(1)

(2)

式中，U—— 线圈电压

R—— 线圈电阻

L—— 线圈电感

I—— 线圈瞬态电流

i0—— 线圈初始电流

td—— 滞后时间

电磁力Fm公式为：

(3)

式中，N—— 线圈匝数

μ0—— 真空磁导率

A—— 衔铁有效截面积

l0—— 初始气隙长度

x—— 阀芯位移

由式(2)、式(3)可得，增加占空比D，电磁力Fm上升区间增长，下降区间减少，因此提高占空比D，可等效增加电磁力的稳态平均值Fem。

阀芯开启时，机械动力学方程为：

(4)

式中，m—— 阀芯质量

k—— 弹簧刚度

Fq—— 液动力

B—— 速度阻尼系数

Ff—— 摩擦力

液动力Fq简化计算公式为[12]：

(5)

式中，Cd—— 流量系数

Cv—— 流速系数

A0—— 阀口过流面积

Δp—— 阀口压力差

α—— 阀口射流角

w—— 阀口面积梯度

ld—— 油液阻尼长度

ρ—— 油液密度

阀芯关闭时，机械动力学方程为：

(6)

式中，x0为弹簧初始压缩量。

式(4)、式(5)中摩擦力Ff在阀芯未被推动时，由于阀芯与阀体的静摩擦作用，摩擦力较大；当阀芯推动后，由于阀芯周围被油液包围，摩擦力可忽略不计，因此在阀芯开启初始时刻，应适当增加占空比，从而增大电磁力，减少阀芯推开的响应时间。在阀芯关闭时刻，由于液动力、黏性阻力、摩擦力的共同作用，存在滞后性；因此，在压力控制过程中，当实际压力接近目标值且压力变化率过快时，应提前减小占空比，减小电磁力，提前缩短阀芯开口长度，减少滞后时间，从而减小压力超调量。

黏性阻力与液动力受油管长度、温度等因素影响，液压回路中的油液阻塞问题同样无法避免，因此需要保证设计的算法能够满足复杂时变环境要求，能够根据工作环境变化，自动调整占空比，以实现不同电磁力的输出。

3 控制算法设计

3.1 自学习阶段

设置升压/降压自学习方波自适应调整充液阀与排液阀的阈值占空比Don_thr，Doff_thr，当工作环境改变，出现制动缸压应力响应时间过长或超调量过大时，触发自学习指令，进入自学习阶段，重新调整阈值占空比值，自学习算法流程如图3所示。

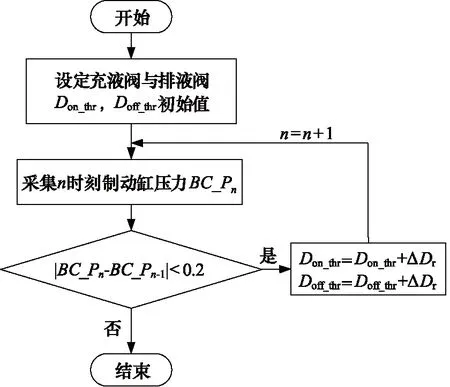
图3 自学习算法流程图Fig.3 Flowchart of self-learning algorithm

以相邻时刻制动缸压力差作为阀芯推动判据，当进入自学习阶段时，不断累加阈值占空比值，如式(7)、式(8)所示：

(7)

(8)

式中， ΔDr—— 占空比自学习累加值

当|BC_Pn-BC_Pn-1|>0.2 MPa时，判断阀芯已推开，阈值占空比自学习完成，退出自学习阶段，进入压力控制阶段。

3.2 压力控制阶段

压力控制阶段采用混合脉宽激励——“积分+斜率”控制算法，如图4所示。

初始时刻，进入混合脉宽激励环节，先采用单个大脉宽(2Don_thr/2Doff_thr)激励，再采用多个小脉宽(1.2Don_thr/1.2Doff_thr)，在保证压力控制不出现超调问题的同时，尽可能减少阀芯推动的空走时间。

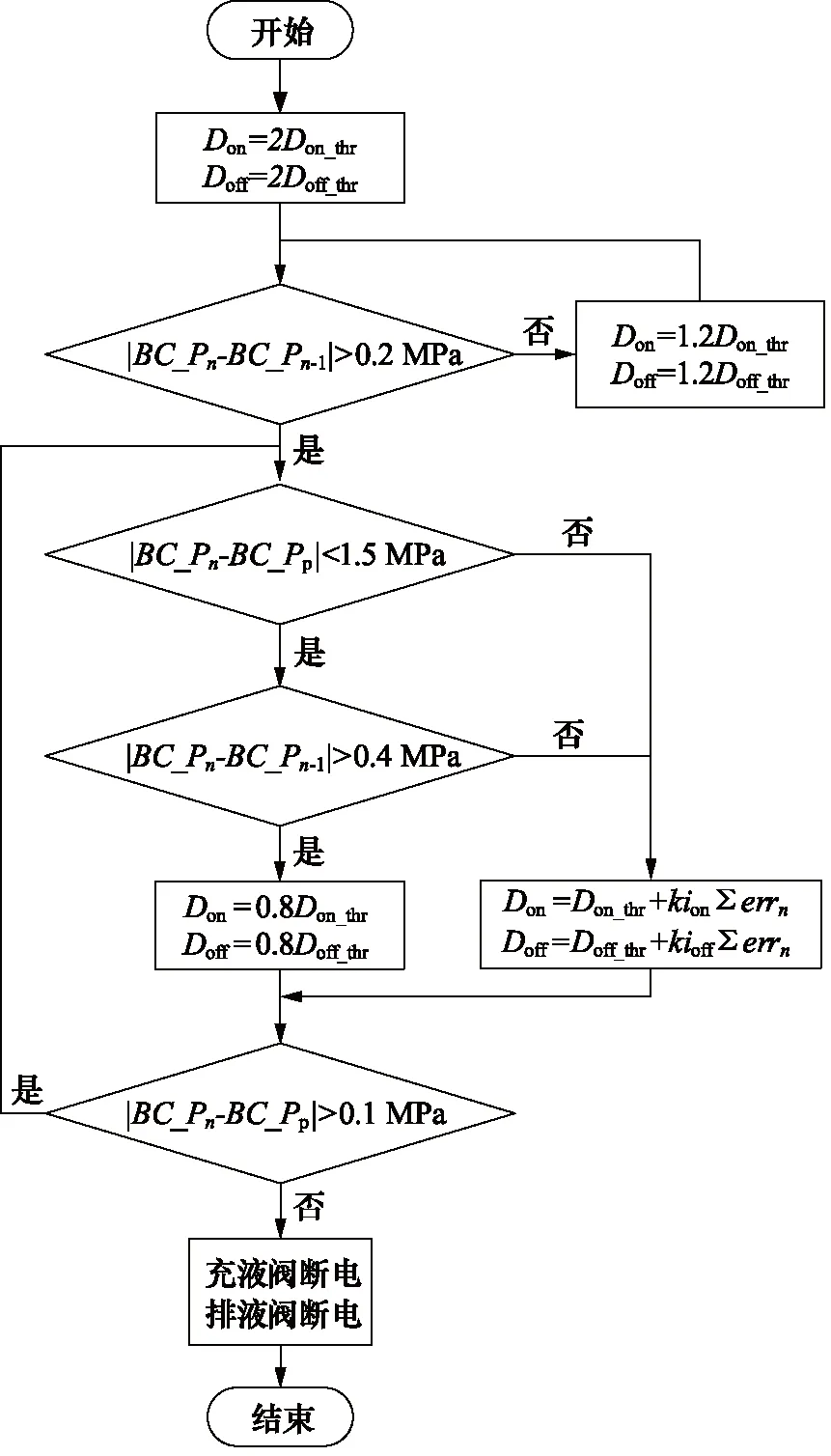
图4 压力控制算法流程图Fig.4 Flowchart of pressure control algorithm

当满足|BC_Pn-BC_Pn-1|>0.2 MPa时，阀芯推开进入积分控制环节，如式(9)、式(10)所示：

Don=Don_thr+kion∑errn

(9)

Doff=Doff_thr+kioff∑errn

(10)

式中，errn——n时刻实际压力与目标压力差值

kion—— 充液阀积分系数

kioff—— 排液阀积分系数

当制动压力实际值与目标值接近(|BC_Pn-BC_Pp|<1.5 MPa)时(BC_Pp为制动缸目标压力)，且压力上升/下降斜率过大(|BC_Pn-BC_Pn-1|>0.4 MPa)时，进入压力变化斜率调整环节，缩小占空比(0.8Don_thr/0.8Doff_thr)提前减小阀芯开度，以缩短阀芯关闭时的滞后时间，从而减少压力控制过程中的超调量，提高系统稳定性。

当满足|BC_Pn-BC_Pp|<0.1 MPa时，制动缸压力误差控制在许可范围内，封锁脉冲，充液阀与排液阀同时断电，以提高高速开关阀的使用寿命。

4 实验验证

采用德国HAWE高速开关阀(开启平均响应时间为15 ms，关闭平均响应时间为25 ms)搭建实验台，如图5所示。实验台包括电脑监控、EBCU控制器、压力传感器(量程为0～16 MPa，频率为1 kHz)液压单元、蓄能器、制动缸5部分。给定方波、正弦波形式的压力控制目标值，观测曲线响应情况，计算动态和稳态误差值。

图5 高速开关阀控制实验台Fig.5 High-speed on-off valve control test bench

方波跟随曲线如图6所示，实际压力曲线采用滑动平均滤波处理，初始时刻处于升压/降压自学习阶段，压力响应时间长；当自学习阶段结束，进入压力控制阶段时，压力响应时间不超过250 ms，超调量不超过0.25 MPa，稳态误差控制在0.1 MPa内。

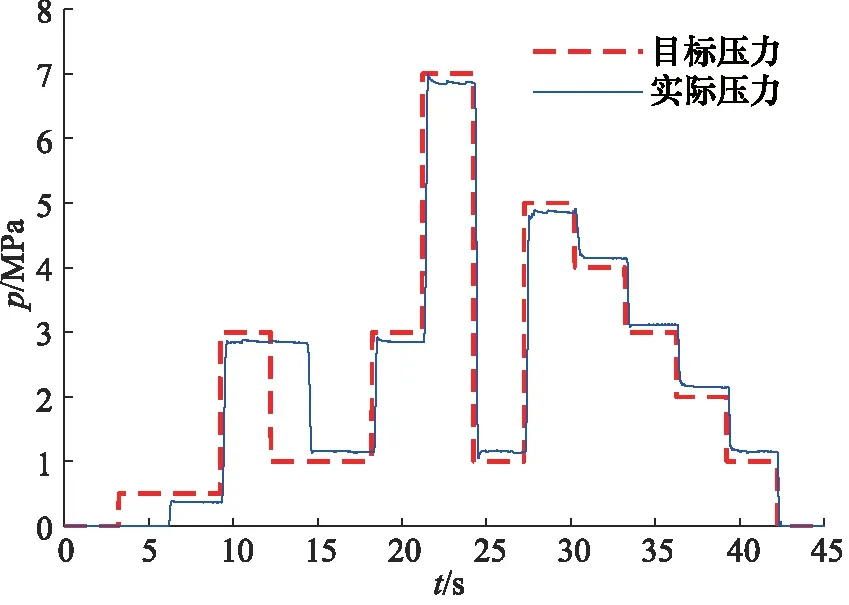
图6 常温方波跟随曲线Fig.6 Normal temperature square wave following curve

1 Hz正弦波跟随曲线如图7所示，在自学习阶段结束后，跟随曲线基本保持一致，动态跟随性能良好。

为验证复杂时变环境工况对算法鲁棒性的影响，搭建高低温实验台，如图8所示，分别进行55 ℃高温实验与-40 ℃低温实验。

图7 常温1 Hz正弦波跟随曲线Fig.7 Normal temperature 1 Hz sine wave following curve

图8 高低温实验台Fig.8 High/Low temperature test bench

高温方波跟随曲线如图9所示，在高温下，压力响应时间增加，但仍不超过350 ms；方波跟随中无超调量，稳态误差控制在0.1 MPa内。

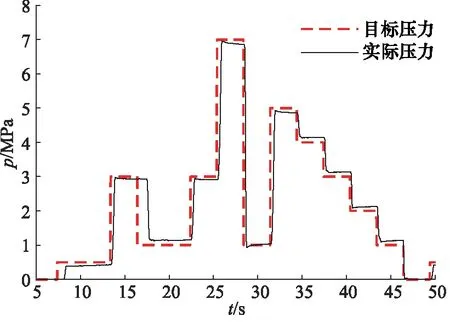
图9 高温方波跟随曲线Fig.9 High temperature square wave following curve

高温1 Hz正弦波跟随曲线如图10所示，在高压时刻，动态跟随曲线存在一定量滞后时间，但无明显相位差，动态跟随性能保持良好。

通过图11与图12曲线发现，低温工况下方波跟随时在25 s处出现微小超调，超调量不超过0.1 MPa，稳态误差控制在0.1 MPa内；1 Hz正弦波跟随时无明显相位差，跟随性能良好，因此，本研究算法能够适应高低温复杂时变环境下的压力稳定控制，鲁棒性与自适应性良好。

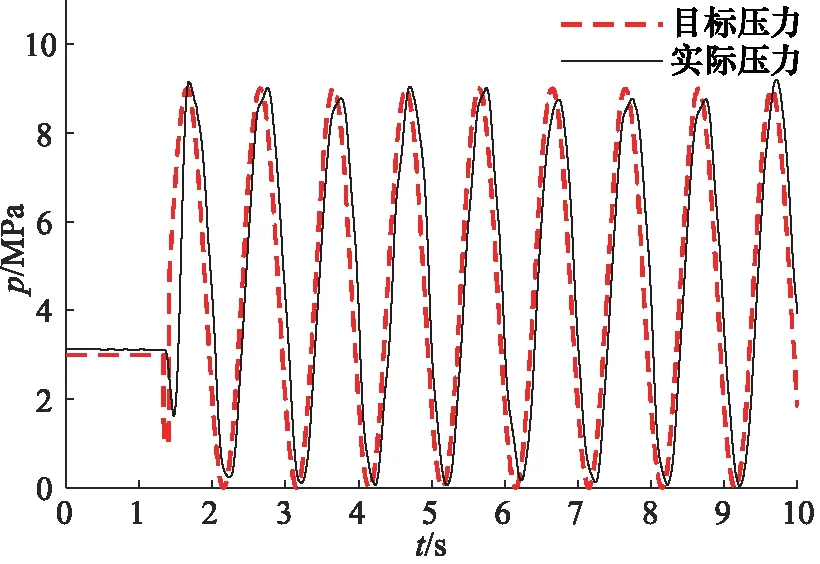
图10 高温1 Hz正弦跟随曲线Fig.10 High temperature 1 Hz sine following curve

图11 低温方波跟随曲线Fig.11 Low temperature square wave following curve

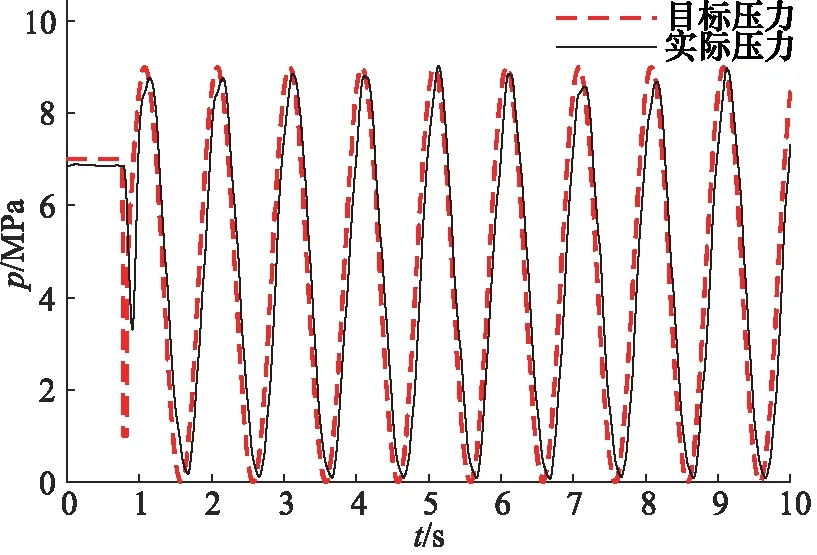
图12 低温1 Hz正弦跟随曲线Fig.12 Low temperature 1 Hz sinusoidal follower curve

5 结论

本研究在高速开关阀数学模型分析基础上，提出了阈值占空比自学习的高速开关阀自适应控制算法，通过自学习阶段自适应调整阈值占空比。在不同环境温度实验工况中，稳态误差不超过0.1 MPa，响应时间不超过350 ms，超调量不超过0.25 MPa，且1 Hz正弦波曲线动态跟随时，无明显相位差，跟随性能良好，此算法具有良好的鲁棒性和自适应性，能够良好适应复杂时变环境的控制需求。