基于格子Boltzmann方法的静压转台流场动态分析

常 斌， 段鸾芳

(1.江苏联合职业技术学院泰兴分院机电工程系， 江苏泰州 214599；2.南京工业职业技术大学电气工程学院， 江苏南京 210023)

引言

《中国制造2025》中明确提出高档数控机床和机器人是十大重点发展领域之一，高档数控机床的高速、高精、高效发展有助于推动我国制造业的创新升级[1-2]。转台作为高档数控机床中的关键部件，对数控机床的可靠运行起着至关重要的作用。静压转台由于油膜具有吸振作用且摩擦系数小，已广泛应用于重载场合。前人针对静压转台提出了诸多腔体结构，并对油液的流动进行了深入探讨[3-4]。

在结构方面，王永柱等[5]利用Fluent对矩形油垫中的油腔结构进行了分析， 结果表明口字形比工字形结构具有更好的承载能力。刘云鹏等[6]设计了一种新型静压转台，解决了重载下油膜厚度较小，流入流量小于泄漏量的问题。王京等[7]设计了一种双环形油腔，并探究了入口雷诺数对油液在油腔内部及油腔承载能力的影响。张庆锋[8]利用CFD对数控磨床扇形静压转台的油膜特性进行了分析。在承载力方面，安汝伟等[9]对定量闭式静压转台的支承力进行了等效计算。刘志峰等[10]利用有限差分法研究了油垫温度与重载静压转台承载力之间的关系。陈令等[11]利用ANSYS研究了大型立式磨床静压工作台在不同转速下的油膜温升结果。刘志峰等[12]针对定量扇形静压转台探讨了整体动力学模型，并通过实验进行了验证。申峰等[13]利用PIV和CFD分析了数控机床静压系统中的流场特性。刘赵淼等[14]探讨了入口油液雷诺数对静压油腔承载能力的影响，雷诺数的变化将改变流线中涡的位置。

本研究将针对油液在环形静压转台内部的流动展开研究，利用LBM重点研究封油边间隙高度、入口速度及油液黏度3个因素对油液流动、速度分布及承载能力的影响。

1 LBM方法

LBM具有物理过程清晰，计算方便，易编程实现等优点，已广泛应用于工业制造领域[15-17]。其将流体流动看成是微观粒子在不同方向的运动，根据运动情况主要包含迁移和碰撞两种情形[18]，LBM的一般性方程如式(1)所示：

fi(r+eiδt,t+δt)-fi(r,t)=

(1)

式中,fi—— 某时刻的瞬时运动方程

r—— 位移

t—— 时间

ei—— 速度配置

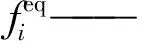
在二维流动中常用D2Q9(二维九向)模型，其速度配置具体为：

(2)

式中,e—— 基本速度

e取决于格子步长δx和时间步长δt，具体为e=δx/δt。式(1)中τ为松弛时间，其与动力黏度μ相关，如式(3)所示：

(3)

式中，ρ—— 密度

(4)

式中，ωi—— 权重系数

cs—— 格子声速

u—— 速度

ωi与粒子运动方向相关，其具体数值为：

(5)

(6)

密度ρ与速度u的表达式如式(7)所示：

(7)

在对实际问题仿真分析时，具体流程如下：

(1) 量纲转换，LBM为无量纲方法，在实际分析时，需要进行实际物理量与计算物理量的转换，此处以雷诺数作为准则数；

(2) 确定计算域及初始条件(如初始速度、初始密度、初始压力、雷诺数、松弛时间、流体黏度等)；

(3) 根据式(4)确定平衡态分布方程；

(4) 根据式(1)进行分析计算，包含迁移和碰撞2个步骤；

(5) 进行边界处理，这里采用常用的非平衡外推格式[19-20]；

(6) 根据式(7)计算密度和速度；

(7) 设定一较小误差值，计算上一循环步与当前循环步之间的差值，当此差值小于设定的误差值时，则满足精度要求，跳出循环，否则转至步骤(3)继续执行下一次循环计算；

(8) 根据步骤(1)中的量纲转换，反向计算宏观物理量值。

2 油腔外形参数及仿真方案

静压转台双环形的油腔如图1所示，其具体参数如表1所示。

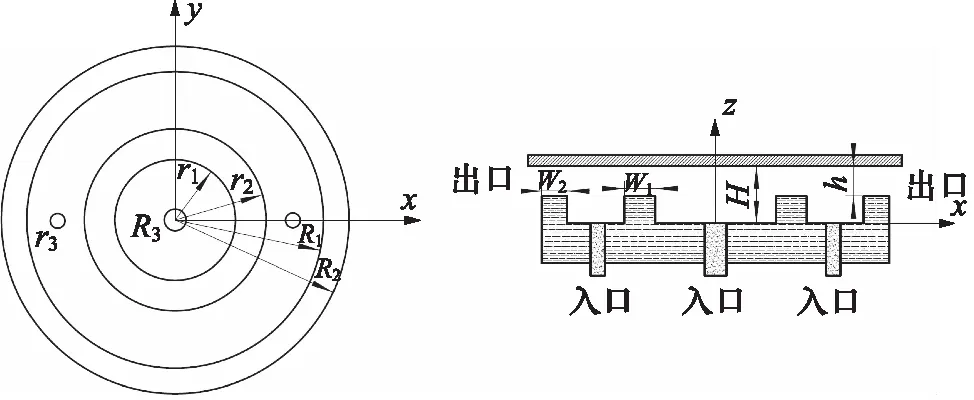
图1 双环形油腔

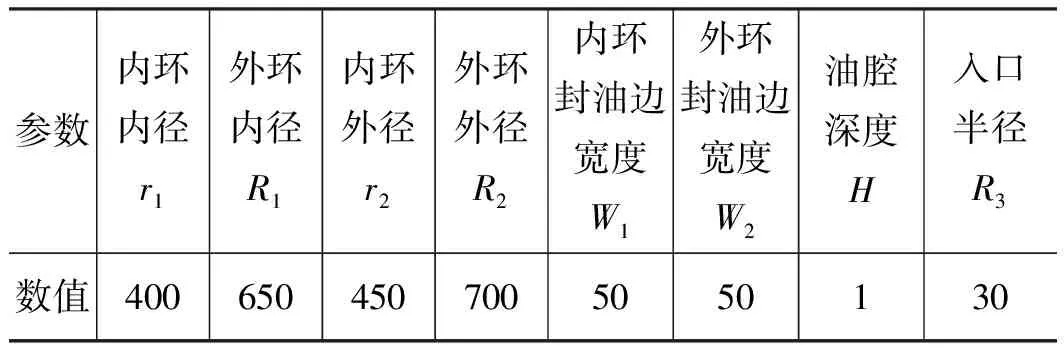
表1 双环形油腔的几何参数Tab.1 Geometry parameters of double rings oil chamber mm

为了充分考虑不同因素对油液在油腔内流动的影响，选取封油边间隙高度、油液入口速度以及油液黏度3个因素进行深入分析，共列出如表2所示的7种组合方案，其中油腔深度H设定为11 mm。由于油腔结构具有对称性，为了节省计算资源，取其中一半结构进行分析。利用MATLAB结合LBM方法，对表2中的7种方案进行了仿真分析，获得的流线图如图2所示，颜色越深表示涡的程度越强烈。

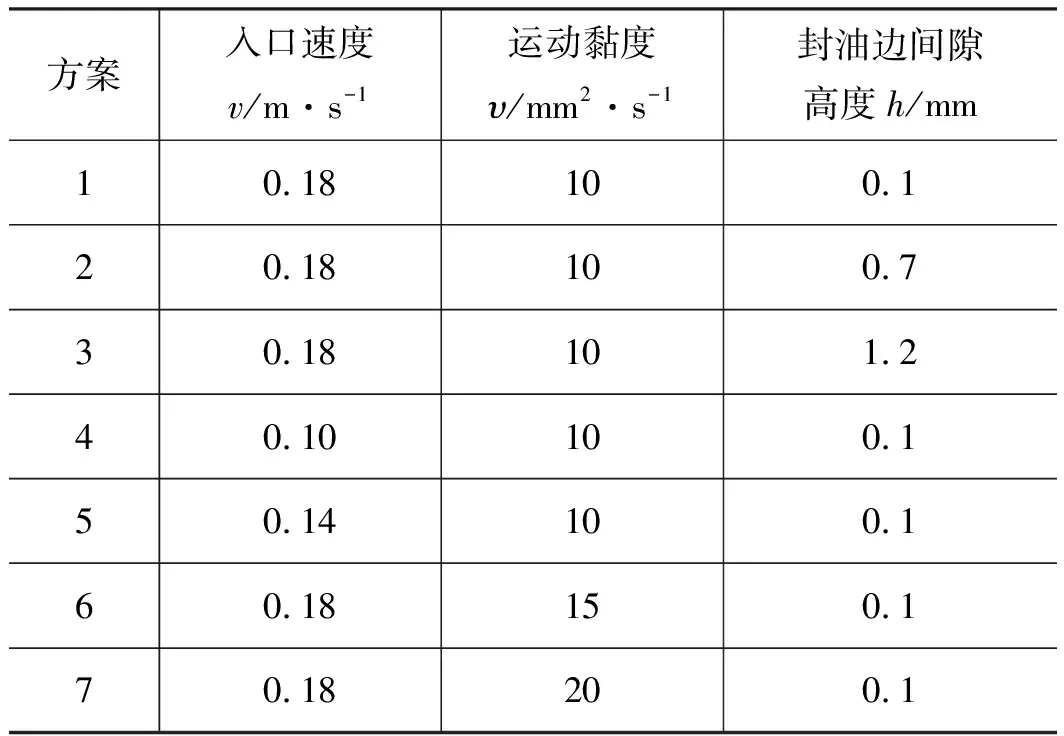
表2 流动仿真方案Tab.2 Simulation cases of flow

3 油液流动分析

3.1 封油边间隙高度的影响

根据图2a～图2c所示，主涡的数量一共有6个，当封油边间隙高度较小时，主涡的强度不一，第一主涡附近有诸多小涡形成，随着封油边间隙高度的逐渐增加，小涡有逐渐融入主涡的趋势，且第一入口引起的涡流会逐渐影响到外侧凹槽区域。封油边处水平速度沿径向的变化曲线如图3所示，主要的区别在内部，其中案例2对应的速度分布差距较大，案例1速度变化相对较小，而在右端出口处速度几乎一致。转台的承载力曲线如图4所示，随着间隙高度的增加，中心凹槽与外侧凹槽内承载力的差值越来越小，在案例3中，中心凹槽与外侧凹槽内的承载力近乎无差别，说明当间隙过大时，环形设置将不再影响转台的承载能力。

3.2 入口速度的影响

根据图2a、图2d、图2e所示，流线图表明入口速度主要影响了第一主涡、第四主涡以及小涡的形成与强烈程度。出口封油边处水平速度沿径向的变化曲线如图5所示，入口速度越大，水平速度沿径向分布的差距越小，当入口速度为0.10 m/s时，速度差距较大，最大差值达到了0.025 m/s，但在封油边出口处的速度几乎均为0 m/s。转台的承载力曲线如图6所示，由图可知，速度越大，承载力越大，而环形设置引起的中心凹槽与外侧凹槽承载能力的差值近乎相等。

3.3 油液黏度的影响

根据图2a、图2f、图2g所示，黏度越大，流线的分布情形越简单，对第一主涡及第四主涡的影响最为明显。出口封油边处水平速度沿径向的变化曲线图如图7所示，黏度对速度分布影响较为明显，但无明显规律，速度波动最明显出现在案例7中，速度波动最小的出现在案例6中，出口速度均为0 m/s，则无油液漏出。转台的承载力曲线如图8所示，黏度较小的案例中呈现出较好的承载能力，随着黏度的增加，中心凹槽与外侧凹槽承载力的差值逐渐增大。

4 结论

(1) 油液封油边间隙高度影响了主涡的形成，尤其体现在第一主涡，随着间隙高度的增加，中心凹槽的区域会逐渐影响到外侧凹槽区域，封油边沿径向的速度受出口间隙高度的影响较明显，且未呈现出特定规律，当间隙较小时，通过环形设置，外侧凹槽的承载能力有明显提升;

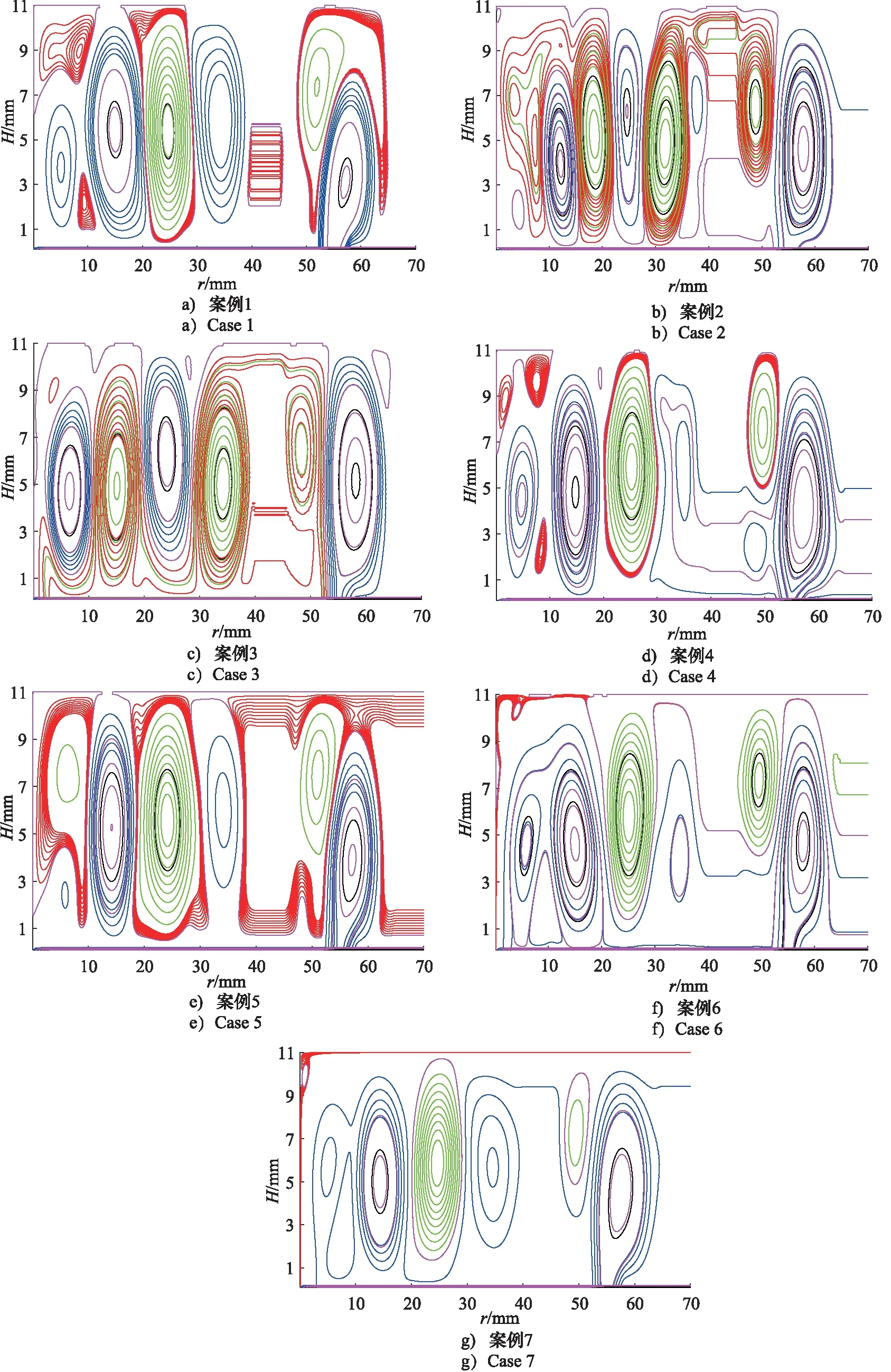
图2 不同案例油腔内部的流线图Fig.2 Streamlines of oil in chamber for different cases

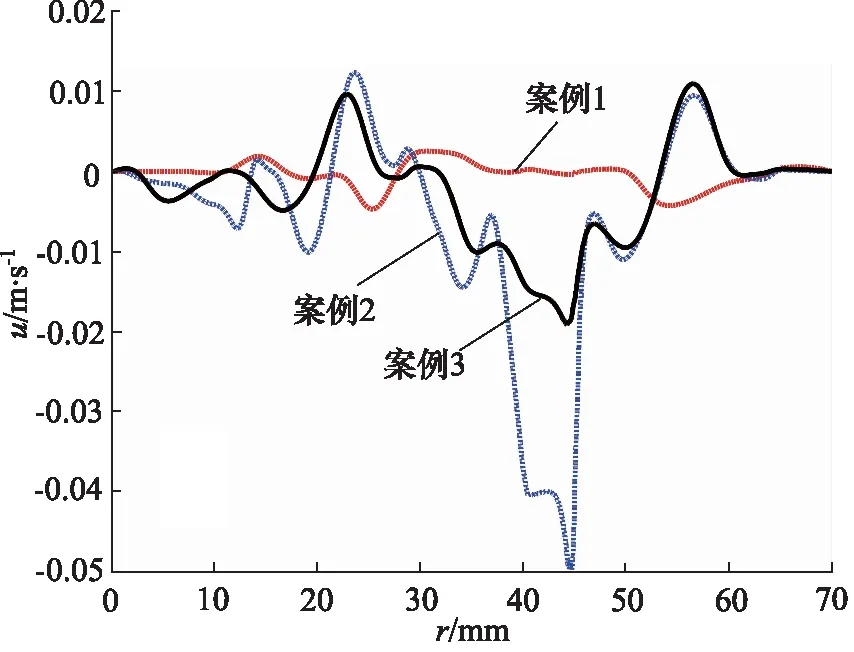
图3 案例1～3的封油边径向速度分布Fig.3 Radial velocity distribution at sealing edge for case 1～3

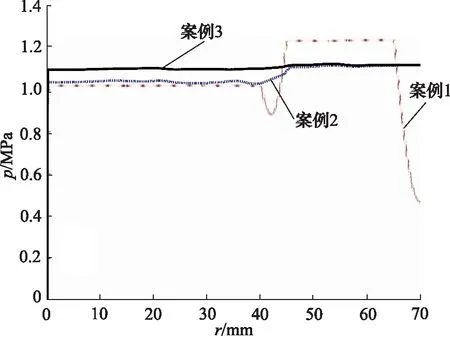
图4 案例1～3的压力分布曲线Fig.4 Pressure distribution curves for case 1～3

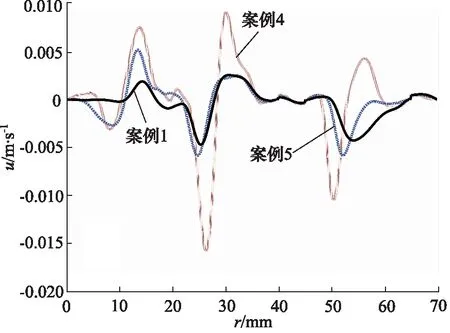
图5 案例4，5，1的封油边径向速度分布Fig.5 Radial velocity distribution at sealing edge for case 4,5,1

(2) 油液入口速度对流线、封油边径向速度分布以及承载能力有明显影响，入口速度越小，封油边径向速度波动越明显，但承载能力越差；

图6 案例4，5，1的压力分布曲线Fig.6 Pressure distribution curves for case 4,5,1

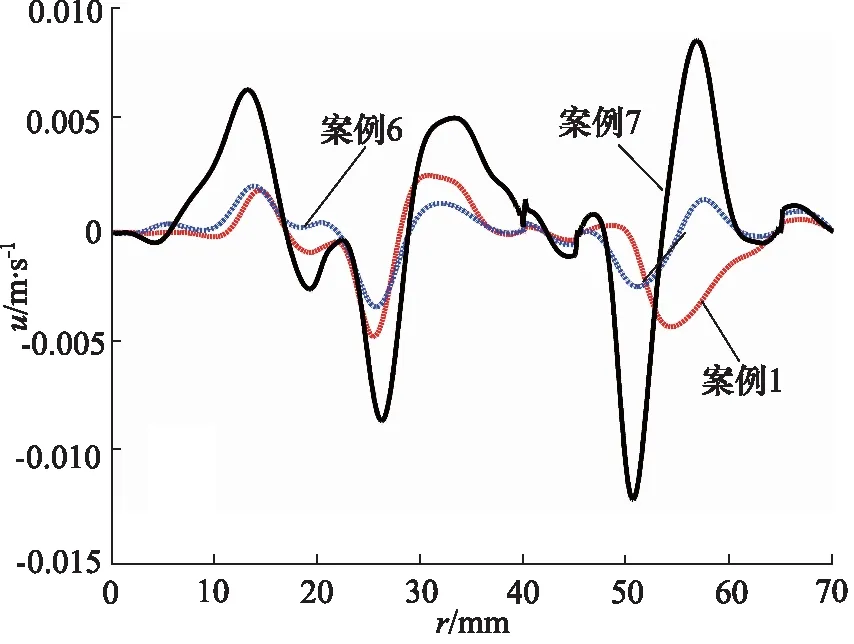
图7 案例1，6，7的封油边径向速度分布Fig.7 Radial velocity distribution at sealing edge for case 1,6,7

图8 案例1，6，7的压力分布曲线Fig.8 Pressure distribution curves for case 1,6,7

(3) 油液黏度对主涡有重要影响，尤其体现在第一主涡和第四主涡上，油液黏度越小，承载能力越好，外侧凹槽与中心凹槽承载力的差值随黏度的增加而增大。