电力系统小干扰稳定分析的最小特征轨迹法

黄 伟，张清波，许 昊，吴司敏，甘德强

（1. 云南电力调度控制中心，云南 昆明 650011；2. 浙江大学 电气工程学院，浙江 杭州 310027）

0 引言

我国电网当前呈现交直流混联及新能源高渗透率的发展趋势，为电力系统小干扰稳定分析带来新的挑战［1］。面对日益复杂的电网，电力系统小干扰稳定分析需从以下3 个层面进行考虑：第一，系统中的控制器（如电力系统稳定器PSS（Power System Stabilizer）和调速器）参数的变化对系统稳定性的影响；第二，系统工况变化（如机组出力连续变化）对系统稳定性的影响；第三，系统模型的变化（如重要元件的投退）对系统稳定性的影响。目前，以PSS 设计为核心的第一层面的问题已被较好地解决［2］，而第二、三层面的问题仍需深入研究。

依据稳定性分析方法及判据的不同，电力系统小干扰稳定分析大致包括5类［3］：基于状态空间系数矩阵特征值分析的方法，常见的方法包括阻尼转矩法［4-5］、留数法［6］、灵敏度分析等；基于传递函数矩阵分析的方法，包括广义Nyquist 判据［7］、μ分析［8］、多回路稳定裕度km法［9］、H∞控制［10］等；基于Lyapunov判据的分析方法［11-12］；基于Mickhailov 定理的多项式分析方法［3］；基于代数判据，如Routh-Hurwitz 判据等。方法虽多但优劣各异，有些方法未推导稳定裕度解析表达式，还有些方法无法分析任意回路对稳定性的影响。

本文提出一种基于广义Nyquist 判据的电力系统小干扰稳定分析方法：最小特征轨迹法。该方法根据简洁形式的转子回路模型得到回差矩阵的最小特征轨迹偏离原点的距离，即系统稳定裕度。推导了最小特征轨迹的近似解析表达式，从而量化了各个控制回路对系统稳定裕度的贡献。所提方法具有比较严密的理论基础，通用性较强，适用于电力系统超低频和低频振荡分析，并且有望被应用于更加复杂的电力系统稳定分析问题。通过仿真算例进一步验证了所提方法理论分析的正确性和工程实用性。

1 小干扰稳定分析的反馈系统模型

小干扰稳定分析Heffron-Phillips 模型［13］如附录A 图A1（a）所示。图中：GM(s)为原动机-调速器传递函数矩阵，HPSS(s)为PSS 传递函数矩阵，M为发电机惯性时间常数矩阵，KD为阻尼系数矩阵，T'd0为直轴暂态开路时间常数矩阵，GEX(s)为自动电压调节器的传递函数矩阵，I为单位阵，以上矩阵均为对角矩阵；K1—K6为与元件参数及运行工况相关的系数矩阵；ΔPe1和ΔPe2分别为通过K1和K2的电磁转矩增量；ΔPm为机械转矩增量；Δω为转速增量；Δδ为转子角增量；ΔE'q为发电机暂态电势增量；ΔEfd为励磁电压信号增量；ΔUPSS为PSS 输出信号增量；ω0为同步转速；s为拉普拉斯算子。

为方便后文推导，对图A1（a）所示模型进行简化。将GM(s)和HPSS(s)的输入由Δω调整为Δδ，可得到图A1（a）的等效框图，如图A1（b）所示。将图中这种以ω0/[s(sM+KD)-1]为前向通道、其余部分为反馈通道的模型称为转子回路模型。在转子回路模型中，将虚线框中以Δδ为输入、ΔPe2为输出的部分定义为GQ(s)。为了方便后续的分析，首先通过简单的等效变换，将GQ(s)分解为不包含HPSS(s)的GQ1(s)和包含HPSS(s)的GQ2(s)，形成简洁形式的转子回路模型，如图1所示。图中存在如下关系式：

图1 简洁形式的转子回路模型Fig.1 Rotor circuit model in concise form

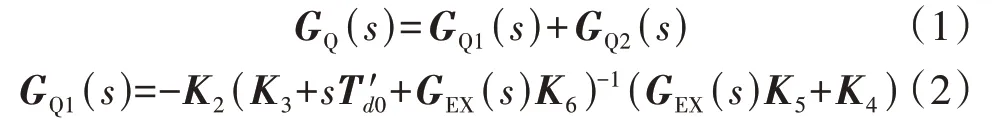
上述简洁形式的转子回路模型更清晰地将多机系统分解为1个前向通道和3个反馈通道的形式，在后文中将使用该形式的模型开展稳定分析。

2 基于最小特征轨迹的稳定裕度

本节将基于简洁形式的转子回路模型并根据多输入-多输出MIMO（Multi-Input Multi-Output）系统的广义Nyquist 判据，推导出基于最小特征轨迹的稳定裕度近似解析表达式。

2.1 基于最小特征轨迹的稳定裕度判据

由图1 中简洁形式的转子回路模型可得系统的回差矩阵D(s)的表达式为：

式中：L(s)为开环传递函数矩阵。将s=jω代入式（4），根据广义Nyquist判据，回差矩阵行列式det(I+L(jω))与坐标原点的距离即为稳定裕度；基于特征轨迹的Nyquist 稳定判据见文献［14］。回差矩阵行列式与系统的特征轨迹关系见式（5）。

式中：k为机组编号；m为电网机组总数；λk(⋅)为矩阵的特征轨迹。由式（5）可知：系统的特征轨迹由回差矩阵I+L(jω)的特征值曲线组成；采用本文所提转子回路模型，特征轨迹数目与机组总数相同。因此当电网有m台机组时，m条特征轨迹围绕原点的环绕次数决定了闭环系统右半平面的极点数。

设λmin(I+L(jω))为I+L(jω)所有特征轨迹中距离原点最近的特征轨迹。当系统处于临界稳定状态时，λmin(I+L(jω))非常接近原点，而其余特征值的模均较大，故采用λmin(I+L(jω))到原点的最短距离d{(0，0)，λmin(I+L(jω))}表示系统稳定裕度。又因为：

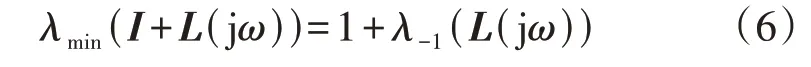
式中：λ-1(L(jω))表示距离点（-1，0）最近的L(jω)特征轨迹。

因此可通过计算λ-1(L(jω))到点（-1，0）的最短距离d{(-1，0)，λ-1(L(jω))}，来表示系统稳定裕度，并将d{(-1，0)，λ-1(L(jω))}所对应的特征值称为最小模特征值或最小特征值。显然，当λ-1(L(jω))=0时，闭环系统存在一个位于虚轴的特征值，此时系统处于临界稳定状态。

2.2 基于最小特征轨迹的稳定裕度近似解析表达式

最小特征值需要经过复杂的计算才能精确获得，且难以直观表现稳定裕度与电网参数的关系，不便于开展稳定分析。本节对矩阵L(jω)进行相似变换，得到一个对角占优矩阵，其最小模对角元近似等于最小特征值，避免了迭代计算最小特征值，同时能够得到反映各个回路对最小特征值影响的解析表达式。由式（4）可知：

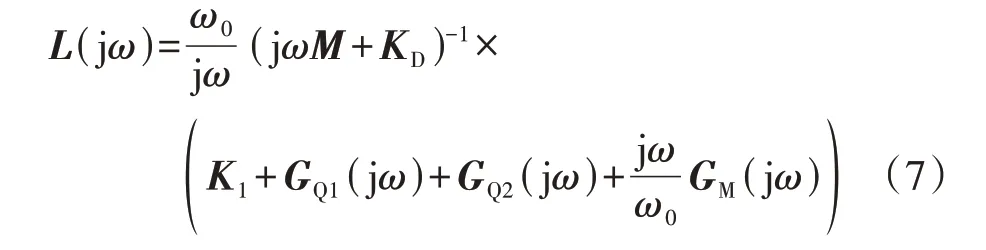
由于M、KD均为对角矩阵，故可将(jωM+KD)-1分解为：

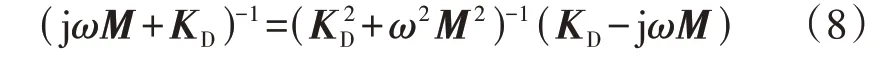
将式（8）代入式（7）后可得：

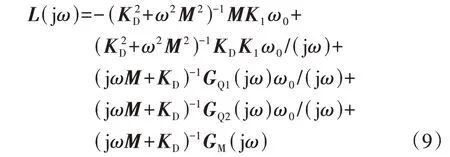
为便于分析，将式（9）的各个分式分别定义为K1相关回路LMK(jω)、阻尼相关回路LKD(jω)、励磁相关回路LGQ1(jω)、PSS相关回路LGQ2(jω)以及原动机-调速器相关回路LGM(jω)，并将除LMK(jω)以外的另外4个分式之和表示为ΔL(jω)，即：

则有：

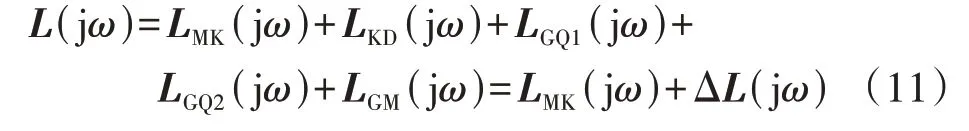
为简化表述，除特殊说明外，后文中所有出现的频率响应矩阵或者由频率响应矩阵决定的其他矩阵或变量均省略(jω)。可以注意到LMK为实数阵。由于一般情况下矩阵K1可对角化且LMK的特征值及特征向量通常为实数，对LMK进行特征分解后可得：

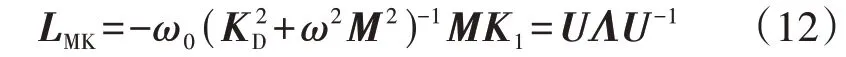
式中：Λ为特征值矩阵；U为右特征向量矩阵。将式（12）代入式（11）可得：

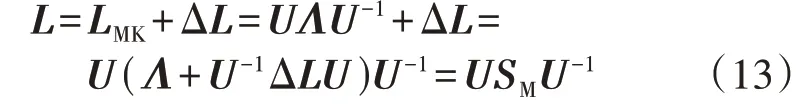
式中：SM为L的相似矩阵。由相似矩阵的性质可知：

至此，原问题转化为计算L的相似矩阵SM特征值问题，即：

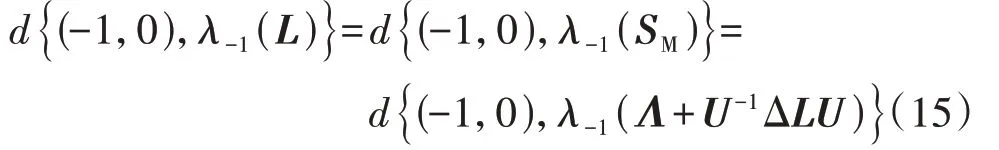
相似矩阵SM具有很明显的对角占优特性。例如，一个6 机11 节点算例系统的相似矩阵对角元几乎对应于SM也即L的全部特征值，这意味着相似矩阵的最小模对角元可作为系统稳定裕度。这是因为机电暂态模型中，假设KD≈0，矩阵LMK≈-ω0M-1K1/ω2，这在很大程度上影响了L的特征值。

而在相似矩阵SM中，ΔL为包含电力系统控制回路的频率响应矩阵LGQ2、LGM的线性表达式，即：

假设相似矩阵SM第1 行第1 列元素SM，11即为最小模元素，根据上文分析，新的稳定裕度SM，11具有很强的单输入单输出SISO（Single-Input Single-Output）系统参数裕度特征［15］，数学关系简单。下面将利用这一特点对原动机-调速器回路及PSS 回路对稳定裕度的影响展开分析。

3 原动机-调速器回路对稳定裕度的影响

基于第2 节推导的内容，本节将具体分析原动机-调速器回路对稳定裕度的影响。在相似矩阵SM中原动机-调速器分量为：

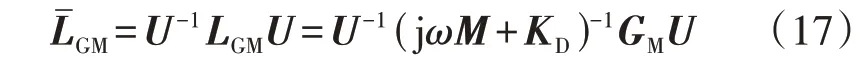
设V=(U-1)T为左特征向量矩阵，则式（17）可变为：

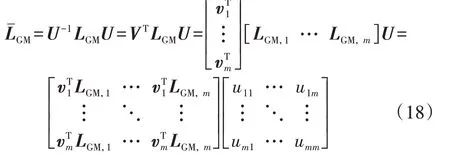
当SM，11为最小模对角元时，可以将其看作稳定裕度。根据式（16）及式（18），原动机-调速器系统对稳定裕度的影响体现在第1 行第1 列元素，的表达式为：

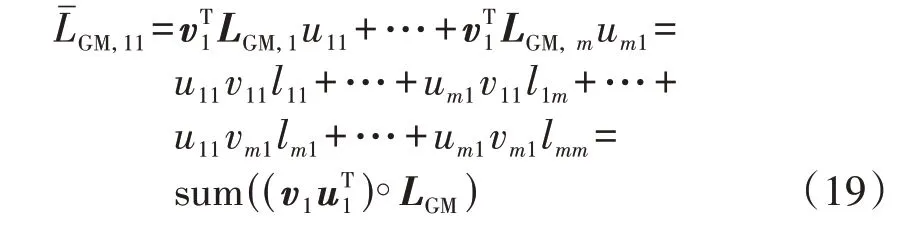
式中：vij为中第i个元素；lij为LGM，j中第i个元素；u1、v1分别为第一个特征值对应的右、左特征向量；“∘”表示其左右两侧矩阵的Hadamard 积；sum（·）为矩阵中所有元素的求和函数。由式（19）可知原动机-调速器回路对SM，11的作用仅取决于最小特征值对应的特征向量u1、v1，与其他特征向量无直接关系。

将LGM代入式（19），由于LGM为对角矩阵，则有：

式中：GMi、Mi以及KDi分别为GM、M以及KD的第i个对角元。式（20）为原动机-调速器传递函数与稳定裕度关系的解析表达式。由于在低频段和超低频段最小特征轨迹基本平行并靠近实轴，弱阻尼时其在实轴以下，负阻尼时其在实轴以上。且一般情况下，u1、v1中各项为正实数，这意味着稳定分析中只需关注各原动机-调速器传递函数在虚轴上投影值的正负情况即可。如果GMi的相角滞后，且大于90°，则结合式（20）可以判断原动机-调速器对应的分量在虚轴上的投影值为正，这意味着该分量使得最小特征值靠近原点，恶化稳定性。

以水电机组和火电机组为例，分析其调速系统对超低频振荡模式的影响。水电机组原动机-调速器模型GMh(s)如下：

式中：KP为比例系数；KI为积分系数；KD为微分系数；TG为伺服系统时间常数；TW为水流惯性时间常数；bp为永态下垂系数。火电机组原动机-调速器模型GMs(s)如下：

式中：TGS=1/(KR)为调速器响应时间常数，R为调速器下垂系数，K为调速器积分环节增益；TCH为高压蒸汽容积时间常数；TRH为再热器时间常数；FHP为高压缸产生功率在总汽轮机功率中占比。显然，水轮机的相频特性大幅滞后于汽轮机，如果调速器参数整定不当，则易产生超低频振荡。这与采用传统的统一频率模型获得的结论［16］一致。

区域振荡和局部振荡的分析方法与超低频振荡类似，仅根据各机组GMi的相角即可判断其对稳定性的影响：当GMi的相角滞后且超过90°时，将削弱系统稳定性；当GMi的相角滞后但是未超过90°时，可以增强系统稳定性。而在低频段GMi的输出有所降低，可忽略其影响。

4 PSS回路对稳定裕度的影响

本节重点分析了PSS 对稳定裕度影响。ΔL中与PSS相关的分量LGQ2表达式为：

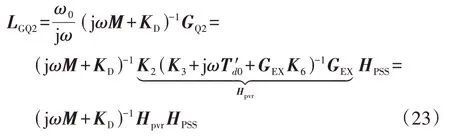
式中：Hpvr为PSS输出信号经过的前向通道的传递函数矩阵［17］。

设fi为矩阵(jωM+KD)-1Hpvr的第i个列向量，hi为各PSS的传递函数，可得：

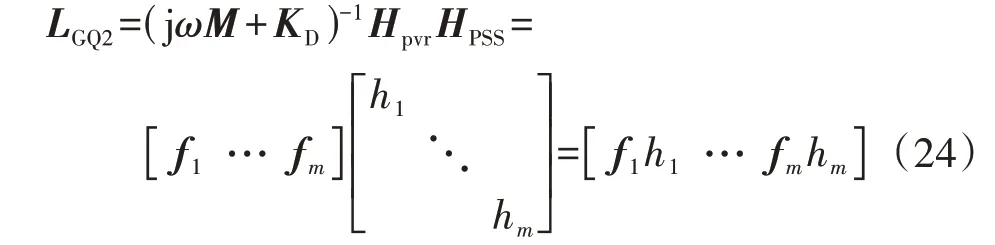
相似矩阵SM中与LGQ2相关的分量的表达式为：

设fij为fj中 第i行 元 素，可 得PSS 对SM，11的 贡献为：

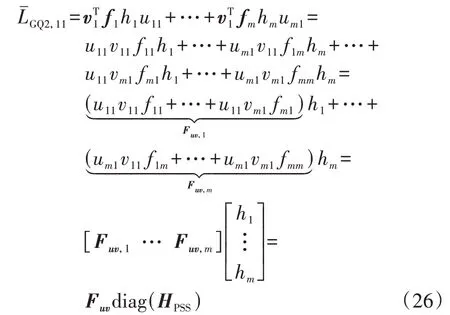
式中：diag(HPSS)为由HPSS矩阵对角元组成的列向量；Fuv，i为式中相应元素之和。由式（26）可知，PSS对SM，11的作用可以由各PSS 传递函数线性相加得到。除分析作用外，式（26）还可以用作PSS 参数整定，此时Fuv的作用与留数类似，能够据其推知PSS中应该补偿的角度。

进一步证明利用最小特征轨迹法对PSS 参数进行整定与理想相频特性法所得结果的一致性。由式（26）可知，最小特征轨迹法中PSS 对稳定裕度的贡献可等效为各PSS 传递函数的线性叠加，故以1 台PSS为例进行介绍。考虑一个有3台同步机的电网，那么PSS对该电网稳定裕度的影响为：

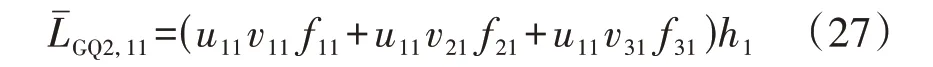
根据式（27），PSS 的参数应该满足式（28）所示相角条件，使得最小特征轨迹“垂直下移”，尽量远离复平面点实轴处的点（-1，0）。

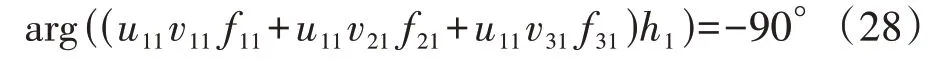
式中：arg（·）为求相角函数。在超低频振荡和区域振荡模式频段，矩阵Hpvr严格列对角占优（即矩阵中每个主对角元素的模都大于与其同列的其他元素的模的总和），此时f11≫f21+f31，又有向量u1、v1中的元素均为正实数，故式（28）可以简化为：

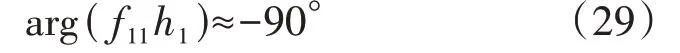
在局部振荡模式频段，矩阵v1呈现“一元独大”的结构，即只有1 个对角元素非常大，其余所有元素都非常小。此时式（29）的准确度更高。而理想相频特性法中根据Hpvr的对角元相角整定PSS参数，即根据式（30）所示条件进行整定［17］。

再根据fij的定义，即：

由式（30）、（31）可得：

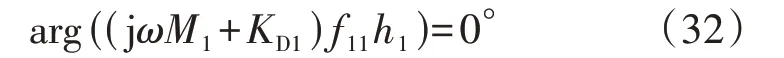
当KD1=0时，有：

综上所述，理想相频特性法与最小特征轨迹法所得的PSS 补偿相角基本一致。另外，在超低频段，Hpvr(jω)的对角元相角接近0°，由上面2 种方法推得PSS 需要补偿的相角也接近0°，这又进一步验证了传统阻尼转矩法的结论［18］。

5 算例分析

本节首先应用最小特征轨迹法计算原动机-调速器回路对低频振荡模式的影响，以及PSS 回路对超低频振荡模式的影响。然后采用最小特征轨迹法、理想相频特性法以及留数法对PSS 输出的补偿相角进行计算，并对结果进行分析比较。最后在IEEE 6 机11 节点、IEEE 19 机118 节点、新西兰10 机39 节点、波兰2 383 节点系统中进行验证。算例中，一半负荷采用恒定功率模型，另一半负荷采用恒定阻抗模型。

5.1 原动机-调速器回路对低频振荡模式的影响分析

在IEEE 6 机11 节点系统中设置0.505 Hz 低频振荡，基于最小特征轨迹法计算了系统中的6 台原动机-调速器系统对系统稳定裕度的影响，结果如图2 所示。图中，圆盘刻度代表相角，向量代表式（20）中相加的各个表达式，向量数目与机组数目一致，向量的模值在本文中不做讨论。由图可知，水电机组原动机-调速器回路对系统稳定性产生了负面影响，即相应的向上的向量使得最小特征轨迹向着包络点（-1，0）的方向移动，其原因在于水电机组固有的非最小相位特性（即水电机组相频响应特性大幅滞后）。相反，火电机组的原动机-调速器回路对系统稳定性产生了正面影响，即其对应的向量使最小特征轨迹向远离点（-1，0）的方向移动。

图2 IEEE 6机11节点系统各机组原动机-调速器回路对稳定裕度的影响Fig.2 Influence of each unit prime motor and governor loop on stability margin of IEEE 6-machine 11-bus system

5.2 PSS回路对超低频振荡模式的影响分析

本节利用最小特征轨迹法，计算IEEE 19 机118节点系统中安装PSS 后输出的补偿相角，并对安装PSS 后对系统稳定性的影响进行分析，如图3 所示。本文IEEE 19 机118 节点系统中未安装PSS 的机组共14台，因此图中的向量个数为14。由式（26）可得Fuv各元素，即为图3 所示14 个向量，再由式（29）得到各机组PSS的补偿相角，其值约为-5°。

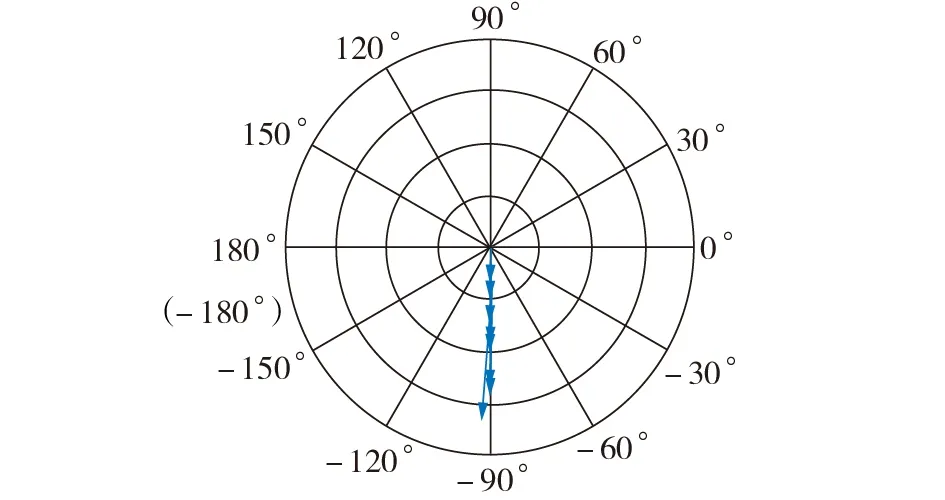
图3 IEEE 19机118节点系统超低频模式下的Fuv中向量Fig.3 Vectors of Fuv for ultra-low frequency oscillation mode of IEEE 19-machine 118-bus system

常规的双输入型电力系统稳定器PSS2B（dualinput Power System StaBilizer）在超低频段只有隔直环节sTW（1+sTW）起实质性作用，取TW=5 s，此时PSS2B 的补偿相角约为30°，仍然贡献阻尼但并非最佳补偿角度。而多频段稳定器（以PSS4B 型多频段PSS为例，下文简称PSS4B）的补偿相角接近于0°，更接近本算例中需要补偿的角度。分别给出未安装PSS、安装PSS2B 以及PSS4B 时系统在超低频段的最小特征轨迹，如图4 所示，图中箭头表示从0 扫频到0.1 Hz时最小特征值的移动方向。

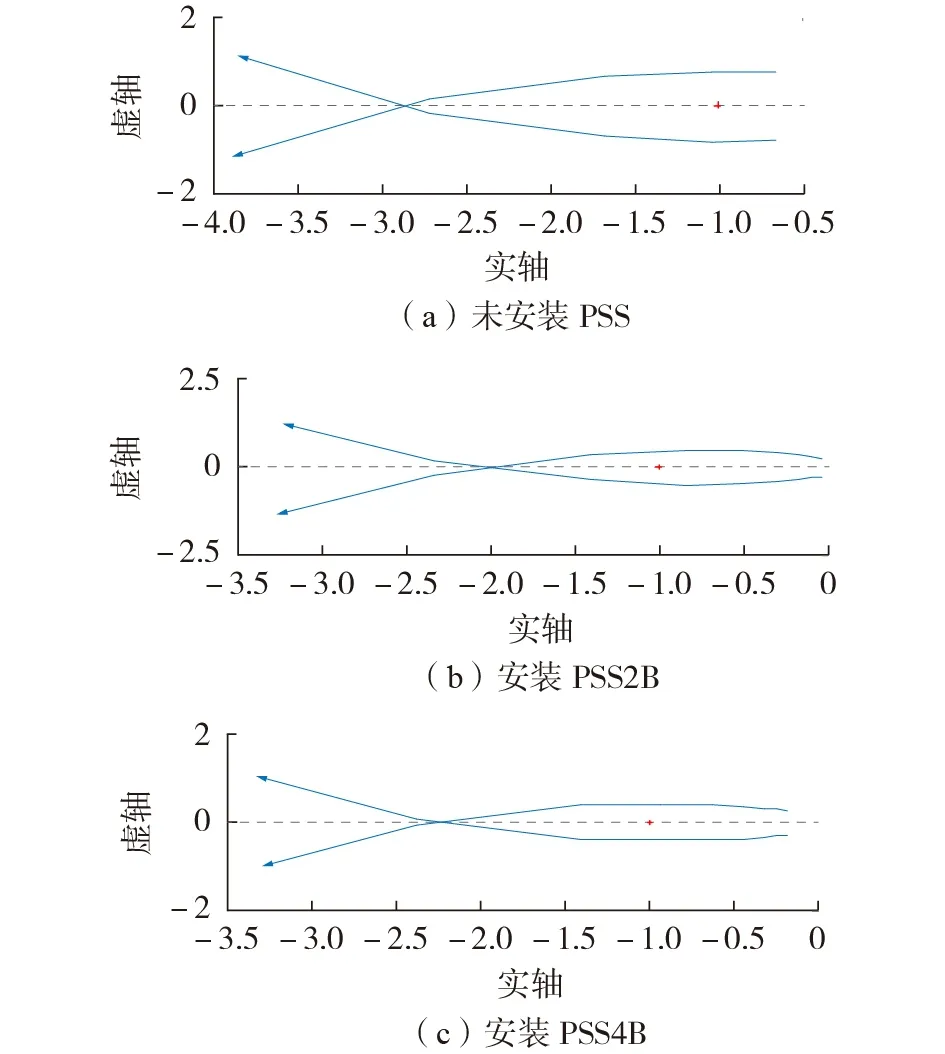
图4 IEEE 19机118节点系统在PSS的3种安装情况下超低频段最小特征轨迹Fig.4 Minimum characteristic locus of IEEE 19-machine 118-bus system under 3 kinds of PSS installation situations

由图4（a）可知，未安装PSS 时最小特征轨迹包络点（-1，0），意味着此时系统处于负阻尼状态，且最小特征值为（-1，j0.798）。由图4（b）可知，安装PSS2B 后最小特征值为（-1，j0.441），特征轨迹向着不包络点（-1，0）的方向移动。由图4（c）可知，安装PSS4B 后最小特征值为（-1，j0.389），特征轨迹进一步向不包络点（-1，0）的方向移动。

5.3 不同系统下PSS的相角补偿结果

以IEEE 6 机11 节点、新西兰10 机39 节点以及波兰2 383 节点系统为例，分别采用最小特征轨迹法、理想相频特性法、留数法对各机组进行PSS 相角补偿计算，计算结果分别见附录A 图A2—A4，图中蓝色向量与-90°之间的相角即为PSS需要补偿的相角。由图可知3 种方法计算的补偿角度基本一致，进一步证明了最小特征轨迹法的准确性。

5.4 特征轨迹稳定裕度与特征值稳定裕度的对比

为了验证最小特征轨迹法求取稳定裕度的准确性，在IEEE 6机11节点系统中设置受端有功负荷由1.55 MW 逐步增加为2 MW，分别利用常规特征值法和本文所提最小特征轨迹法计算系统的临界特征值。将特征值法求得的临界特征值实部作为系统的稳定裕度，将最小特征轨迹法求得的最小特征值虚部作为系统的稳定裕度，二者的对比结果见附录A图A5。由图可知，2 种方法下系统稳定裕度的变化趋势具有一致性，证明了最小特征轨迹法求取稳定裕度的准确性。

6 结论

最小特征轨迹法是SISO 系统的向量裕度法在MIMO 系统中的扩展。初步研究表明，结合本文提出的相似变换技巧，最小特征轨迹法具有SISO 系统向量裕度法的优点，采用该方法后系统的稳定裕度可通过向量线性叠加的解析关系进行简单表示。计算结果表明，最小特征轨迹法能够有效地分析各回路和各机组对系统稳定性的贡献，并为控制器参数的整定提供方向。

附录见本刊网络版（http：//www.epae.cn）。