基于高斯混合模型及近似线性规划的风电系统校正控制方法

周海强，赵春祝，顾婷艳，薛 峰，高 超，宋晓芳

（1. 河海大学 能源与电气学院，江苏 南京 211100；2. 国电南瑞科技股份有限公司，江苏 南京 211106；3. 智能电网保护和运行控制国家重点实验室，江苏 南京 211106）

0 引言

静态安全校正控制是电力系统安全稳定控制的重要环节［1］，系统运行过程中，电源及负荷功率随时可能发生变化，线路开断、设备故障等事故也难以避免，一旦出现线路过载、电压过低等静态不安全现象，必须及时采取合适的校正控制措施，以避免引发连锁反应，造成更大范围的事故。截至2021年11月14 日，我国风电并网装机容量已突破3 亿kW［2］，为了实现我国政府提出的碳达峰和碳中和目标，未来以风电、光伏为代表的新能源占比势必会不断提高。新能源的大量接入，以及温控负荷、电动汽车和微电网等广义负荷的广泛使用，增强了电力系统源荷双侧的不确定性，给电力系统的频率安全、电压稳定等带来了重要影响。如何在计及不确定性的条件下进行风电系统校正控制决策是一个亟待解决的问题。

国内外学者对不确定系统的校正控制问题进行了大量研究，现有方法主要有场景法、机会约束规划CCP（Chance-Constrained Programming）方法、鲁棒优化方法等。文献［3］应用场景法研究了风电系统的静态电压校正控制问题，采取的校正措施包括发电机功率再调度、需求响应、切负荷等。场景法以各种场景下控制代价（或静态安全指标）的期望值为目标函数，其约束条件包括各种场景下的潮流方程和安全约束不等式。场景的数量和代表性对解的精度影响较大，其计算量较大，一般场景法需要应用高效率抽样方法及场景削减技术生成场景集［4］。文献［5］假设新能源预报误差服从高斯分布，基于直流潮流法和CCP方法研究了使用移相器控制以及高压直流功率调制进行过载校正控制的问题。CCP 方法在一定的置信度水平下进行决策，可兼顾控制代价及安全风险，但CCP 方法只能处理不确定变量服从某些特定分布的情况，而对于非线性不确定系统则缺乏系统的求解方法。鲁棒优化基于不确定性参数“最不利”的情况进行最优决策［6］，其控制策略较为保守，经济性较差。文献［7］应用分布鲁棒线性优化理论研究了考虑风电波动的电力系统静态安全校正控制问题，实现了控制策略经济性与鲁棒性的相互转化，在一定程度上提高了鲁棒控制策略的经济性。

总体而言，目前不确定性系统的校正控制方法还存在一些不足。①对于非线性确定性系统的校正控制问题，内点法、连续线性规划方法［8］、粒子群优化算法［9］等求解方法已较为成熟，但对于非线性不确定系统，其求解方法仍在发展之中。②对服从高斯分布的不确定变量研究较多，而对于非高斯分布不确定变量及其相关性考虑相对较少。由于高斯变量的线性组合依然服从高斯分布，故对其进行分析较为方便。但研究表明实际系统中风电及负荷功率预测误差常具有非高斯分布特性，忽略这一特点将导致分析结果有较大偏差。

针对上述问题，本文提出一种基于高斯混合模型GMM（Gaussian Mixture Model）和近似线性规划ALP（Approximated Linear Programming）的风电系统校正控制方法。首先，应用GMM 来描述风电及负荷功率预测误差随机向量的联合概率密度函数PDF（Probability Density Function）及相关性。其次，考虑切负荷、自动发电控制、统一潮流控制器UPFC（Unified Power Flow Controller）等控制措施，建立了计及风电及负荷不确定性的静态安全校正控制优化问题的数学模型。然后，应用灵敏度方法并结合GMM 的性质，将含不确定变量的非线性校正控制问题近似转化为线性规划问题进行求解。最后，以修改后的IEEE 10机39节点系统为例验证了本文所提方法的有效性。

1 风电及负荷功率预测误差的GMM

1.1 风电及负荷功率预测误差的不确定性

建立源荷不确定变量的数学模型是风电系统校正控制的基础。实践中常用预测功率加预测误差来描述实际功率，已有研究常假设风电及负荷功率预测误差服从正态分布，但这一假设往往会存在较大偏差。研究表明风电预测误差的PDF 呈现尖峰厚尾、非对称甚至多峰等特点，并且预测误差的PDF随着风电功率预测值所处区间不同而变化，很难用统一的解析函数来进行拟合［10］。文献［11］指出不同时段和负荷水平下负荷预测误差的概率分布特性差别很大，很难用统一的PDF来描述。

电力系统中各种不确定变量之间存在不同程度的相关性，能否准确地反映其相关性对分析结果影响很大。对于服从高斯分布的相关变量，可以通过Cholesky 分解将其转换为独立高斯变量的线性组合进行分析；而对于非高斯分布的相关变量，尽管可以使用Nataf 变换将其相关系数矩阵转化为高斯变量的相关系数矩阵进行分析［12］，但由于大多数情况下无法获得其解析表达式，故计算过程较为复杂。

1.2 GMM

GMM 以多个正态分布函数的线性加权组合逼近任意PDF，可以描述任意非独立、非正态分布随机变量的联合概率分布。GMM 可根据样本数据直接拟合得到随机向量的联合PDF，并刻画变量之间的相关性，因此，GMM获得了较为广泛的应用。

随机向量X的GMM表达式fGMM(x)如下：

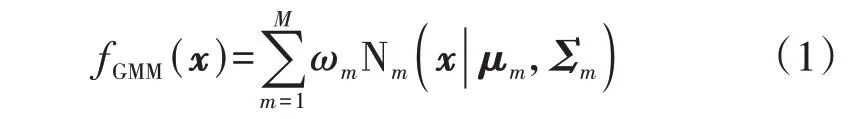
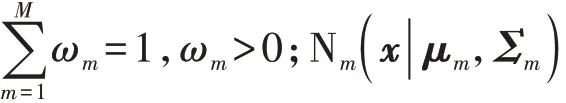
式中：n为样本数；det（·）表示求矩阵（·）的迹。

对于GMM 刻画的多个变量的线性组合，可以方便地获取其GMM。若X为q维随机向量，其线性组合Y=BX+C为p维随机向量，其中B为p×q阶矩阵，C为p维向量，则随机向量Y的GMM 表达式fGMM(y)为［13］：

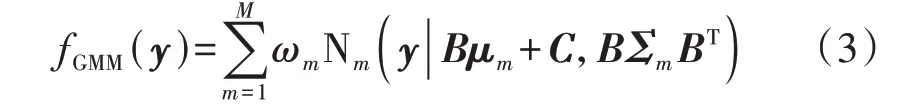
由此可见，若风电或负荷功率为输入变量X，则节点电压、线路潮流等输出变量Y的统计规律可由GMM来描述。

1.3 GMM的参数估计

设X1、X2、…、Xn为 来 自 随 机 变 量X的 样 本，x1、x2、…、xn为样本的一个取值。其对数似然（Loglikelihood）函数fLL(x1，x2，…，xn；θ)为：

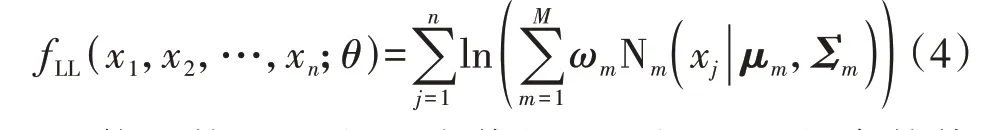
使函数fLL取得最大值的θ即为GMM 的参数估计。θ常采用最大期望算法来获取［14］。最大期望算法通过迭代计算进行参数估计，每次迭代分为2 步：第1 步先根据当前估计的参数θ̂计算函数fLL的期望值；第2 步寻找能使函数fLL期望值最大化的参数值θ，新得到的参数被用于下一次迭代。如此循环，直至函数fLL收敛。

在应用最大期望算法时需要预先确定高斯子项的个数M，增大M可以提高GMM 对目标变量概率分布的拟合精度，但也增加了模型的复杂性，易产生过拟合的问题。为此，可引入赤池信息量准则来评估GMM的性能，其指标γAIC定义如下：

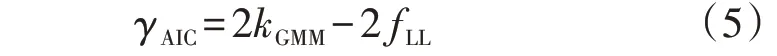
式中：kGMM为GMM 中待估计参数个数。γAIC值越小，GMM性能越优越。

以本文算例中风电场1 的预测误差ΔPw1为例，已知ΔPw1服从TLS（T Location-Scale）分布，其位置参数、尺度参数和形状参数分别为0、0.03 和5。分别采用GMM 和高斯分布模型对其PDF进行拟合，得到拟合曲线见图1，图中风电功率预测误差为标幺值。由图可见，GMM 拟合较好地反映了风电预测误差的“厚尾”特征，其拟合精度优于高斯分布模型。

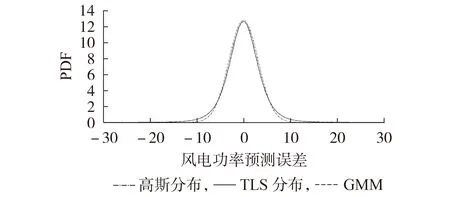
图1 风电功率预测误差PDF的拟合曲线Fig.1 Fitting curves of PDF for wind power forecasting error

2 风电系统校正控制问题的数学模型

新型电力系统中风电、光伏的渗透率不断提高，其不确定性有可能导致常规校正控制策略的失效。同时，随着技术的进步，UPFC、静止无功补偿器等柔性交流输电系统设备的性价比不断提高，在电力系统中的应用日益广泛。因此，本文考虑协调发电机功率调整、UPFC、切负荷等控制措施进行校正控制，在确保系统静态安全的前提下，降低控制代价。

在计及风速及负荷预测误差的条件下，含UPFC的风电系统校正控制优化问题可描述为机会约束规划问题，其目标函数如下：

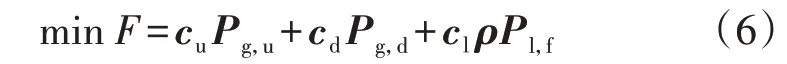
式中：F为校正控制总费用；Pg，u、Pg，d分别为发电机功率的增加量、减少量；cu、cd分别为发电机增、减出力的报价；Pl，f为负荷预测值；ρ为切负荷率；cl为切负荷代价系数。

校正控制优化问题的约束条件如下。

1）含UPFC的电力系统潮流方程。

式中：Xsys、Xupfc分别为系统、UPFC 的状态变量，Xsys=[V，θ，fd]T，V、θ分别为节点电压、相角，fd为静态频率偏差量，Xupfc=[Vse，Vsh]T，Vse、Vsh分别为UPFC串、并联电压源的电压；usys、uupfc分别为系统、UPFC 的控制变量，usys=[Pg，u，Pg，d，ρ]T，uupfc=[Pc，Qc，Vl]T，Pc、Qc分别为UPFC 传输的有功、无功功率，Vl为UPFC 并联变压器所连接的节点电压幅值；Pw、Pl分别为风电、负荷功率。

关于计及频率变化的增广潮流计算及含UPFC系统的潮流计算可分别参考文献［15］和文献［16］，附录A对含UPFC系统潮流计算的原理进行了说明。

2）发电机组出力及爬坡约束。

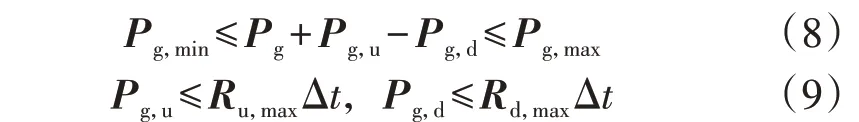
式中：Pg为发电机功率；Pg，max、Pg，min分别为发电机出力的上、下限；Ru，max、Rd，max分别为发电机出力向上、向下调节速率的极限；Δt为校正控制有效时间，可取为15 min。

3）切负荷比例约束。

4）静态频率、电压及线路潮流约束。

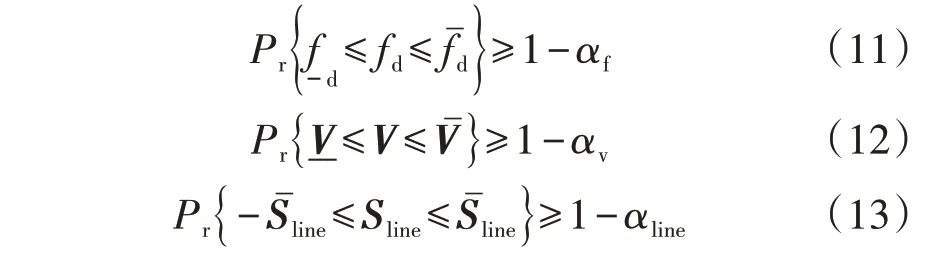
式中：Pr｛·｝为求事件｛·｝发生的概率；、-fd分别为频率偏差的最大值、最小值，本文分别取0.2、-0.2 Hz；、分别为电压上、下限；Sline为线路传输容量；Sˉline为线路传输容量的上限；1-αf、1-αv和1-αline分别为静态频率、电压和线路潮流约束预设的静态安全置信水平。

5）UPFC 安全运行约束。为确保UPFC 安全运行，对其状态变量的取值有一定的限制。

在校正控制优化问题中引入置信度可以兼顾安全风险和经济代价，避免为了满足极少数“高风险、小概率”事件的要求而盲目地提高控制代价。已有CCP 问题的求解方法多限于线性问题及高斯分布的不确定变量，但由于风电系统校正控制问题中潮流方程及UPFC 的数学模型具有强非线性，且一般情况下Pw、Pl的预测误差呈现非高斯分布特性，因此，如何快速、准确地求解式（6）—（14）所描述的非线性CCP问题是有待解决的问题。

3 基于ALP的校正控制问题求解方法

对于非线性CCP 问题，常用的求解方法可以分为如下2 类：一类方法是启发式方法，如粒子群优化算法，由于优化过程中需要评估每个粒子在大量不确定场景下的性能，因此其计算量巨大，算法收敛慢，很难付诸实施；另一类方法设法将非线性CCP问题转化为线性CCP 问题求解，将优化控制问题与非线性潮流计算问题解耦，交替迭代求解［8］，本文基于此提出了一种基于ALP的校正控制问题求解方法。

3.1 基于灵敏度的校正控制问题线性化

校正控制优化问题的任务是寻找确保系统静态安全，且经济代价最小的控制解u=[usys，uupfc]。下文以上标（k）表示迭代过程中第k步的变量取值，下标f表示参数的预测值。在搜索解的过程中，对于任意的初始点u(k)=[，]，通过求解潮流方程式（7）可计算得到预测场景(Pw，f，Pl，f)下系统和UPFC 的状态 变 量=[，]，以 及 线 路 功 率 等 输 出 变量。设ΔPw、ΔPl分别为风电、负荷功率预测误差，则实际场景为(Pw，f+ΔPw，Pl，f+ΔPl)，由于实际场景具有不确定性，故严格意义上，需要通过概率潮流计算来校验控制变量u(k)能否满足安全约束方程式（11）—（14），这一过程计算量很大，而且无法为控制变量u的修正提供有针对性的指导。但如果ΔPw、ΔPl的概率分布可以用GMM 来刻画，则上述过程可以大幅简化。

当预测误差较小时，控制变量u(k)下的状态变量X(k)可近似为：

至此，即可较为方便地考核其是否满足安全约束方程式（11）—（14）。

如果频率、电压、线路传输功率等静态安全置信水平低于预设阈值，则需要对控制变量u加以修正，求出第k+1 步的修正量Δu(k+1)。考虑到Δu(k+1)的作用，式（16）可扩展为：

通过不断地修正控制变量u可以改变各高斯子项的期望，最终使X(k+1)的概率分布满足设定的置信水平。

3.2 机会约束规划问题的求解

由式（19）可知，X(k+1)的累积概率分布函数可以表示为：

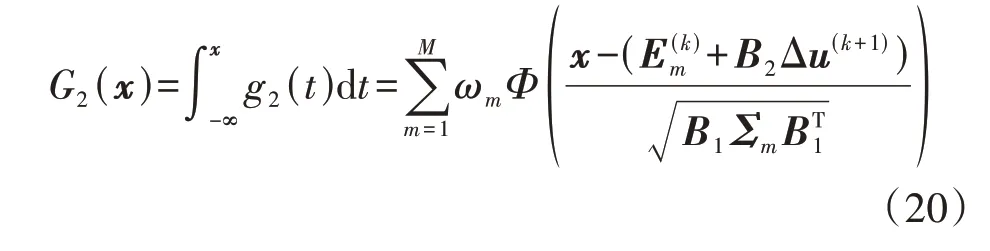
下面以潮流约束方程式（13）为例对其转换过程加以说明，方程式（13）可以等效为以下2个方程：

由于Φ(⋅)为单调函数，且ωm>0，故式（21）、（22）不等号左侧为单调函数，代入不同的Δu(k+1)可以得到不同置信水平，通过二分法可以快速搜索出对应的分位点。

至此，关于线路潮流的概率不等式（13）被转化为关于Δu(k+1)的确定性线性不等式。同样地，可以对静态安全约束方程式（11）、式（12）及式（14）进行类似处理，将其转化为线性不等式，使得式（6）—（14）所描述含不确定性变量的非线性CCP问题在第k步可近似转换为线性规划问题，具体如下：

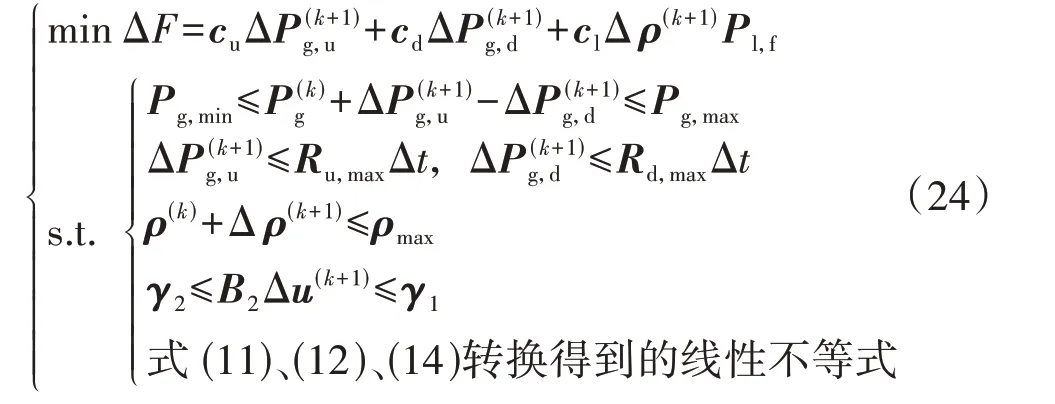
式中：ΔF为迭代过程中相邻两步之间校正控制费用的增量；、分别为相较于第k步，第k+1步发电机上调功率和下调功率的增量；Δρ(k+1)为第k+1步减负荷率的增量。

通过求解问题式（24）可以求出当前的最佳修正量Δu(k+1)，并得到第k+1步的控制变量u(k+1)为：

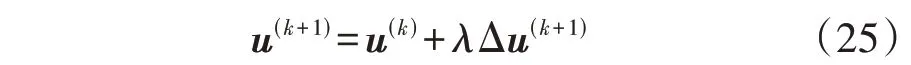
式中：λ为修正系数，一般可取0.3 左右，这是由于灵敏度矩阵B1、B2只在第k步运行点的邻域内具有较高精度，在迭代过程中，对Δu加以限制，可确保求解结果位于近似线性化模型式（24）的有效域内。

同理，由于线性规划问题式（24）的近似性，因此所求得的u(k+1)一般并不是最优解，还需要在此基础上进行迭代计算，直至|Δu(k+1)|≤ε为止，其中ε为预设阈值。

3.3 ALP方法的改进

为了保证ALP 的精度，每次迭代都需要重新计算潮流以及灵敏度矩阵B1和B2，由于含UPFC 系统潮流方程的非线性性质，一般难以获得灵敏度矩阵的解析表达式，因此只能通过数值方法求取B2为：

若系统的控制变量总数为nu，则每次迭代需要进行nu+1 次潮流计算。对于大型电力系统，发电机、可调负荷及UPFC 等控制元件数量众多，故迭代过程中灵敏度更新计算占用了大量时间。

为了减少计算量，需要设法减少参与校正控制的控制变量数目。考虑到扰动后一般只有少数变量严重违反静态安全约束，故可根据校正前系统状态，筛选出若干违约程度较为严重的主导观测变量，重点对其安全性加以校正。对于系统中每个控制变量ui（i=1，2，…，nu），可定义平均灵敏度ζi为：

式中：yk为第k个主导观测变量；Δui为控制变量ui的增量；Δyk为第k个主导观测变量的增量；ui，N、yk，N分别为ui、yk的额定值；nc为主导观测变量的数目。对于发电机和负荷而言，其单位调节量的经济代价已知，此时可以定义计及经济代价的平均灵敏度为：

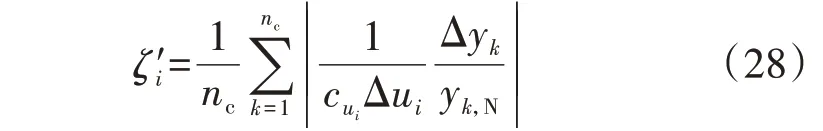
式中：cui为控制措施ui的经济代价系数。基于ζ'i进行控制变量筛选可以更好地反映其经济性能。根据ζi或ζ'i的大小对控制变量进行排序，保留ζi或ζ'i较大的若干个控制变量，在此基础上进行校正控制决策，这样可以有效地减小问题规模，提高计算效率。另外，由于不同控制变量的灵敏度计算互不相关，因此，还可以采取并行处理技术，这样大幅地提高了计算速度。

需要说明的是，尽管近似线性化模型存在截断误差，但由于每一步迭代时均会重新计算灵敏度，更新模型，因此模型误差只会影响下一次迭代的初值，而不会在迭代过程中传递。该方法的主要误差在于采用近似线性化模型求取节点电压、线路潮流等变量的概率分布特性时所产生的误差。但风电及负荷功率的超短期预测误差一般较小，基于近似线性化模型可较为精确地求取其概率分布特性，从而保证优化解的精度。

4 算例分析

为了验证基于GMM 及ALP 的校正控制方法的有效性，将其应用于修改后的IEEE 10 机39 节点系统进行校正控制决策计算，仿真平台为Thinkpad i5 2.3 GHz，仿真软件应用MATLAB 2016a，其中线性规划调用linprog（·）函数进行求解。

4.1 算例系统

修改后的IEEE 10 机39 节点系统结构如图2所示，其详细数据见文献［17］，系统基准容量为100 MV·A。为了研究风电不确定性对校正控制决策的影响，将节点32、37处的同步发电机替换为2座风电场WT1、WT3，并在节点17 加装了1 座风电场WT2，WT1—WT3的有功功率预测值分别为6.5、2、5.4 p.u.，风电及负荷功率预测误差分别服从TLS 分布及高斯分布，相应参数及其GMM 如附录B 所示。同步发电机输出功率上、下限及功率调整代价因子见附录C 表C1，各负荷节点的可控比例及代价因子见附录C表C2，各线路的传输极限见附录C表C3。

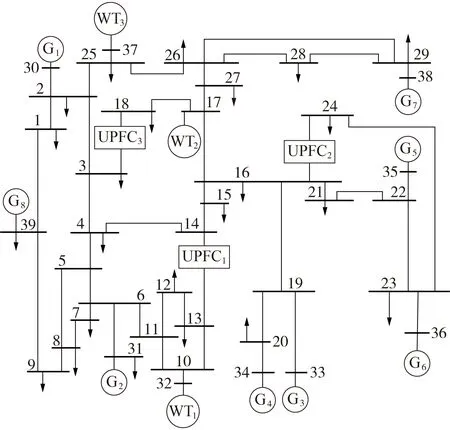
图2 修改后的IEEE 10机39节点系统结构Fig.2 Structure of modified IEEE 10-machnie 39-bus system

假设算例系统中节点15处的负荷增加250 MW，应用计及相关性的拉丁超立方抽样方法［18］对风电及负荷功率预测误差进行抽样，生成3 000 个样本，在此基础上对系统静态安全性进行考核。计算结果表明，扰动后系统静态频率偏低，且线路13-14、15-16、21-22 将以较大概率出现过载。以线路13-14 为例，扰动前、后线路传输容量的PDF 如图3 所示，图中线路传输容量为标幺值，后同。

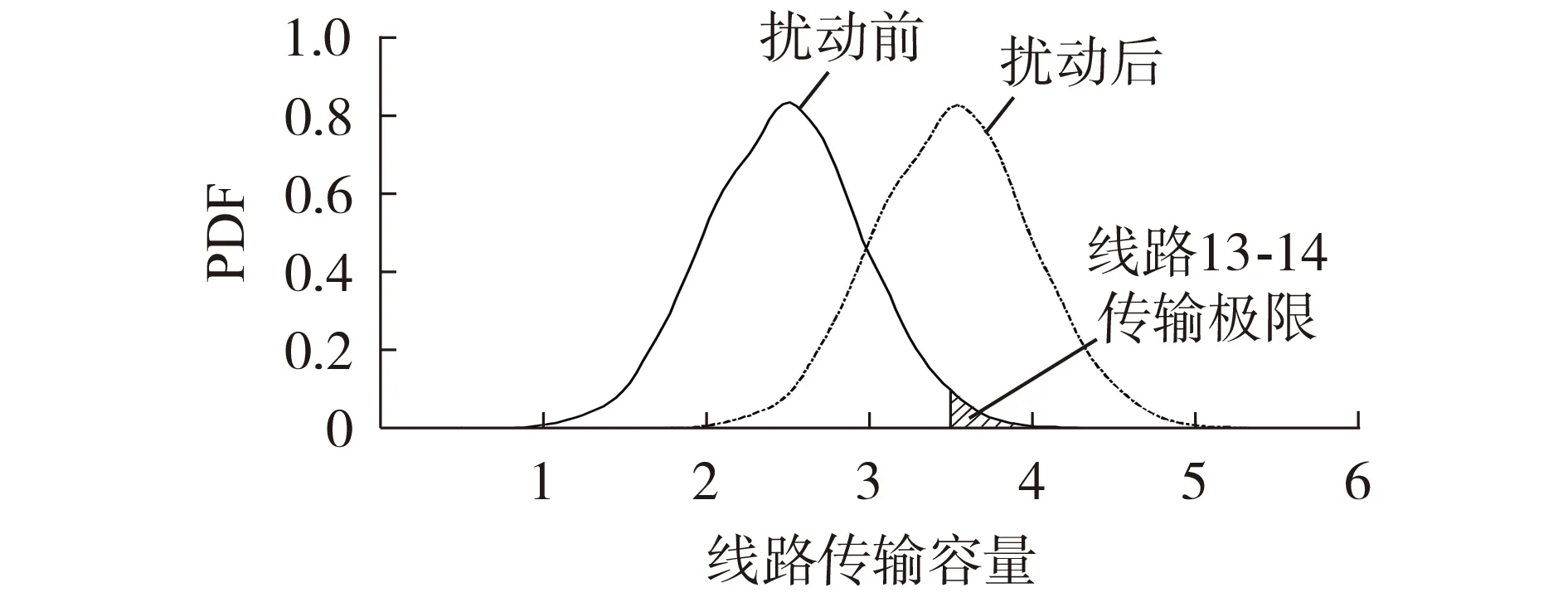
图3 扰动前、后线路13-14传输容量的PDF对比Fig.3 Comparison of PDF for transmission capacity of Line 13-14 between before and after disturbance

由图3 可见：扰动前线路13-14 输送功率的期望为2.47 p.u.，线路过载的概率约为1.73%（见图3 中阴影部分）；扰动后该线路过载的概率大幅增加，约为52%。由此可见，扰动后系统的静态安全置信水平较低，需要采取校正控制措施。考虑到UPFC 能够灵活地调节线路潮流，为了降低控制成本，提高控制能力，在线路13-14、21-24、3-18 分别装设了3 台UPFC，其参数相同，如附录C表C4所示。

4.2 校正控制策略分析

取静态安全约束置信水平1-αf、1-αv、1-αline及1-αu均为98%，阈值ε=0.003，基于风电及负荷功率预测误差的GMM，应用ALP 方法对扰动后的系统进行了校正控制决策。计算结果表明，节点9 和节点25 需要分别切除4.34、40.99 MW 负荷，节点36发电机出力减少4.5 MW，校正控制前、后UPFC 控制变量设定值见表1，校正控制总代价为$ 338.1。表中，Pc、Qc、Vl、Vse、Vsh均为标幺值。

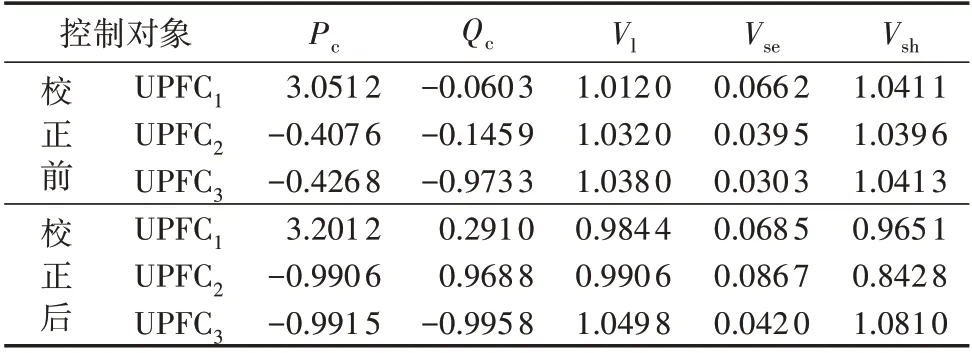
表1 校正前、后UPFC控制变量设定值Table 1 Setting values of UPFC control variables before and after correction

为了验证上述校正控制方案的有效性，同样基于3 000 个样本场景，对校正控制后系统的静态安全性进行了统计分析。图4 给出了校正控制前、后部分线路传输容量的PDF 对比。由图可见：线路15-16、21-22 传输容量上限分别为4.5、6.8 p.u.，校正前线路15-16 发生过载现象的概率达到60.57%，而线路21-22 的过载概率更是高达80.43%；经过校正控制后，线路15-16、21-22 越限的概率分别降低至0.6%、1.03%，满足预设的置信水平要求。

图4 校正控制前、后部分线路传输容量PDF对比Fig.4 Comparisons of PDF for transmission capacity of partial lines between before and after corrective control

校正控制前、后系统静态频率偏差fd的PDF对比如图5 所示，图中频率偏差为标幺值。设定的频率偏差最大值为0.2 Hz，即0.004 p.u.。由图5 可见：扰动前fd的期望为-0.000 3 p.u.，fd处在安全区间内；扰动后，fd的期望跌落到-0.002 3 p.u.，其低于-0.004 p.u.的概率约为2.37%，不满足给定的置信水平要求。校正后由于切除了部分负荷，fd期望值增加到-0.001 2 p.u.，其低于-0.004 p.u.的概率为0.133%，满足给定的置信水平要求。此外，分别设置信度为98%、95%及92%，对校正控制方案及其经济代价进行了计算，结果见附录D 表D1。由表可见，控制代价将随着置信水平的提高而增加。

图5 校正控制前、后系统频率偏差PDF对比Fig.5 Comparison of PDF for system frequency deviation before and after corrective control

在校正控制决策过程中，算法迭代40 次后收敛，控制变量最大修正量随迭代次数增加而变化的曲线如附录D 图D1所示。若不采取任何改进措施，则整个决策过程计算耗时约1.5 h，这是由于本文算例中控制变量u包括21 个切负荷量、8 个发电机功率调整量以及3组UPFC 控制变量，控制变量总数为38 个，故为了更新灵敏度矩阵，每次迭代需要进行39次含UPFC系统的潮流计算。

为了提高计算效率，可根据3.3节所提方法对控制变量进行筛选。本文算例中，违约较为严重的主导观测变量为S15⁃16、S21⁃22、S16⁃19、S16⁃21及fd，计算各控制变量对主导观测变量的平均灵敏度，其中S15⁃16为线路15-16 的传输容量，S21⁃22、S16⁃19、S16⁃21含义类似。对于UPFC，本文不计其控制代价，故采用平均灵敏度ζi，结果见附录E 表E1。可以看到，Vl的灵敏度远大于Pc、Qc的灵敏度，故从3 台UPFC 的控制变量uupfc中选择UPFC1—UPFC3的并联变压器所连接的节点电压幅值Vl1—Vl3作为主导控制变量。对于发电机及负荷，其单位控制代价已知，故采用计及经济代价的平均灵敏度ζ'i，结果见附录E 表E2，从中可筛选出平均灵敏度较大的12 个变量作为主导控制变量。则待优化控制变量的总数由38 个减少到15 个，灵敏度更新时间可节省约60%。由上文计算得到的校正控制策略可以看到，在未对控制变量进行筛选时，校正控制主要通过节点9、节点25处的负荷以及节点36 处的发电机实现，而这些均为附录E表E2中的主导控制变量，这也验证了上述控制变量筛选方法的有效性。在实际工程中，还可以采用并行计算来加快计算速度，最终可以使决策时间达到2～3 min。

4.3 ALP方法与场景法的对比

将基于GMM 及ALP 的校正控制决策方法与场景法进行对比，考虑到算例系统含有24 个不确定变量（3 座风电场和21 个负荷），可能出现的场景数量庞大，为了简化问题，假设所有负荷具有相同的预测误差。应用考虑相关性的拉丁超立方抽样方法生成3 000 个场景，再应用同步回代法进行场景缩减［19］，生成的12 个典型场景及其发生概率见附录F 表F1，在此基础上进行校正控制决策。

场景法包含的变量及约束方程数量众多，是一个大规模的非线性优化问题。为求解该问题，应用GAMS24.7软件进行编程，使用IPOPT 求解器进行求解，求解器迭代2 319 次后收敛，计算用时2 793 s，控制方案代价为$393.9。为了验证所得校正控制方案的有效性，同样基于3 000 个样本场景，对控制方案进行验算，结果表明采用场景法所得控制策略下系统静态安全的概率约为95%。

基于GMM 及ALP 的校正控制方法与场景法的对比如表2 所示。由表可见，基于GMM 及ALP 的决策方法计算速度较快，所得控制策略代价较低，且具有较好的安全性。需要指出的是，基于GMM 及ALP的方法在每一步迭代时实质上是一个机会约束问题，在风电及负荷功率预测误差较小时，它具有较高的精度。而场景法的精度依赖于场景的代表性，一般而言，场景数量越多，其代表性越好，优化计算精度将越高，但计算用时也会急剧增加。因此，典型场景的选取对比较结果有着重要影响。

表2 ALP方法与场景法对比Table 2 Comparisons between ALP method and scenario-based method

5 结论

本文提出了一种基于GMM 及ALP 的校正控制决策方法，主要成果如下：①采用GMM 来描述风电及负荷功率预测误差的联合概率分布特征，较好地考虑了其相关性及概率分布的不规则性；②应用灵敏度分析方法，并结合GMM 的性质将非线性不确定系统的校正控制问题转化为线性规划问题，迭代求解，逐步收敛到最优解；③将该方法应用于修改后的IEEE 10 机39 系统的校正控制决策，并与场景法进行了对比，结果表明，该方法能在确保静态安全的同时，较好地降低控制代价，提高决策速度。

为了提高校正控制决策速度，本文提出了基于并行计算及控制变量筛选的方法，但这些措施在大规模电力系统中的有效性还有待进一步考核，这将是下一步研究的重点。

附录见本刊网络版（http：//www.epae.cn）。