直驱风电场实用化等值方法

齐金玲，李卫星，晁璞璞，李志民

（哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

大力发展新能源，加快构建新型电力系统是实现碳达峰、碳中和目标的基础。随着新能源发电系统在电网中占比的不断增加，其对电力系统安全稳定运行的影响也日益严重［1⁃2］。为了研究大规模风电并网的运行特性，需要建立合适的仿真模型［3］。对风电场内每台风电机组进行建模，可以准确地反映风电场的响应特性，但模型阶数过于庞大，严重影响计算效率，无法满足大规模风电场的并网仿真需求［4］。因此，亟需对风电场进行等值研究。

风电场等值方法可以分为单机等值和多机等值。单机等值将整座风电场等值为1 台风电机组，其容量为所有风电机组的总和［5⁃7］。该方法可显著降低风电场模型的复杂度，大幅提高计算速度，但忽略了机组间运行状态的差异，往往等值精度较低。多机等值法按照预定的分群原则，将具有相同或相近响应特性的风电机组进行归类，采用多台等值风电机组来表征整座风电场，此方法中确定合理的分群指标是关键。

文献［8］考虑尾流效应，将具有相同风速的风电机组分为一群，但在风速分布较分散时，分群数往往过多。文献［9］根据风电机组的地理位置，将同排或同列机组分为一群。然而，当同排或同列机组间风速差异大时，该方法可能会带来较大的等值误差。文献［10］认为变流器电流限幅环节的动作特性主导直驱风电机组的动态行为，并据此提出基于变流器限幅环节动作时间的分群方法，但未考虑故障期间变流器切换至低电压穿越LVRT（Low Voltage Ride-Through）控制策略这一重要因素。文献［11］考虑了不同LVRT 控制策略对风电机组动态行为的影响，提出了通过倍乘等值确定等值机数量的方法，但分群数多，模型不够简化。文献［12］指出故障期间达到电流限幅值的直驱风电机组具有相同的响应特性，可以聚合为一群，而未达到电流限幅值的风电机组，其输出电流随风速变化而变化，需要进行分群等值，但未给出具体的分群方法。文献［13⁃18］将1 个或多个表征机组运行状态的特征量作为分群指标，例如风速、风电机组地理位置、卸荷电路动作状态、有功功率、无功功率、相电流有效值、机端电压、桨距角动作情况、电磁转矩、转子转速等，并结合聚类算法对风电机组进行分群。这种方法通常等值精度很高，但计算复杂，给工程应用带来了困难。为此，文献［19］提出根据故障期间直流电压动态响应的差异，对直驱风电场进行分群。该方法无需依赖聚类算法，计算量小，但未考虑故障清除后风电机组的功率恢复过程。

针对目前已有等值方法存在的工程实用性不足、LVRT 特性考虑不全面的问题，本文提出计及LVRT特性的直驱风电场实用化分群方法。首先，基于从实测数据中提取出的LVRT 响应曲线，对直驱风电机组的故障响应特性和控制策略进行解析。在此基础上，分析风电机组在不同风速下的有功暂态响应特性，根据曲线的聚群特性，初步识别出分割点。然后，通过对比不同电压跌落场景下等值模型的等值效果，进一步探明有效的分割点，提出直驱风电场实用化分群策略，构建直驱风电场三机等值模型。最后，采用多组实测风速数据，对所提等值模型进行有效性验证。

1 直驱风电机组LVRT特性解析

本文对直驱风电机组进行了大量的LVRT 测试，部分测试结果见附录A 图A1。由测试曲线分析风电机组的故障响应特性并提取共性特征，得出了附录A图A2所示的通用LVRT响应曲线。该曲线可以描述故障期间风电机组的无功支撑行为、故障清除后有功功率的斜率恢复过程、故障清除后无功功率的持续支撑及斜率恢复过程等。值得说明的是，不同厂家或不同型号的风电机组，其暂态响应不尽相同，附录A 图A2中的各个阶段不是必须全部包含在模型中，通过调整相应阶段的参数（有功延时tdelay_P、有功恢复速率rP、有功限幅值Pdelay_lim、无功延时tdelay_Q、无功支撑Qsupp、无功恢复速率rQ），该响应曲线可以灵活地模拟不同风电机组的LVRT 响应。表1给出了风电机组在LVRT过程的控制原则。

表1 LVRT全过程的控制原则Table 1 Control principles in complete LVRT processes

由图A2 可知：t1时刻电压由稳态值跌落至0.9 p.u.，风电机组发生低电压故障；t2时刻故障清除，电压开始恢复；t3时刻电压恢复至0.9 p.u.，风电机组检测到故障清除。为便于叙述，将［t1，t2）称为电压跌落期间，［t2，t3］称为电压恢复期间，［t1，t3］称为故障期间。故障期间，风电机组根据并网标准要求优先提供无功功率［20］，无功电流参考值iqref_fault可以表示为：

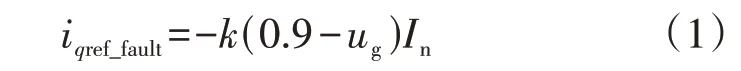
式中：k为无功支撑系数，本文取1.5；ug为电网电压；In为风电机组额定电流。

受变流器容量限制，电压跌落期间风电机组的有功电流参考值idref_fault可以表示为：

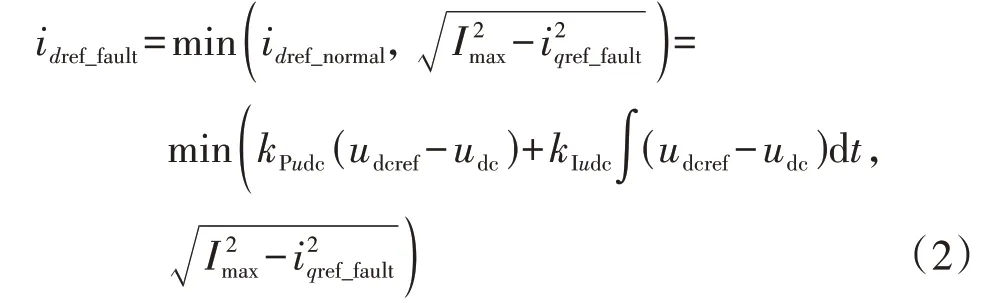
式中：udc和udcref分别为直流电压及其参考值；kPudc、kIudc分别为直流电压外环的比例、积分系数；idref_normal为稳态运行时风电机组的有功电流参考值；Imax为变流器最大允许电流，本文取1.2 p.u.。

t2时刻电压开始恢复，无功指令降低，有功功率增加。为了降低电压恢复时刻（t3时刻）风电机组功率突变对机组和电网的冲击，当前的直驱风电机组通常会限制故障清除后的有功限幅值Pdelay_lim和有功恢复速率rP。因此，直驱风电机组的有功恢复呈现分段特性，即在t2时刻后，随着电压的恢复，有功功率由故障期间的稳态值先恢复至有功限幅值Pdelay_lim，在经过了短暂的有功延时tdelay_P后，按照预设的有功恢复速率rP恢复至有功稳态值P0。值得注意的是，如果风电机组的稳态有功功率小于Pdelay_lim或故障期间的稳态有功功率大于Pdelay_lim，则该限制（即Pdelay_lim和rP）不起作用，有功功率可直接恢复至P0。这2 种情况分别对应稳态功率较小和电压跌落较轻时有功降低较少的风电机组，这些风电机组的有功变化幅度小，其恢复过程对电网的冲击也小，因此可不对有功恢复过程加以限制。综上，电压恢复期间风电机组的有功功率Pvrec可以表示为：

式中：P(t2)为t2时刻的有功功率。在故障恢复期间（（t3，t7］）：当P0Pdelay_lim或P(t2)>Pdelay_lim时，有功功率Pvrec=P0；当P0≥Pdelay_lim且P(t2)≤Pdelay_lim时，有功功率Pvrec的表达式见式（4）。

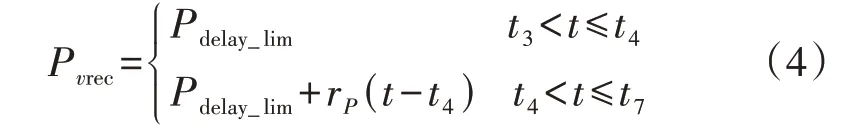
故障清除后，风电机组的无功功率可直接恢复至故障前的无功稳态值Q0，也可以继续提供一段时间tdelay_Q的无功支撑Qsupp，再切换回无功外环控制。类似地，为避免切换过程对电压造成冲击，一些类型的风电机组也会限制无功恢复速率rQ。不同厂家或不同型号的风电机组提供的无功支撑Qsupp、无功延时tdelay_Q及无功恢复速率rQ不尽相同，限于篇幅，本文不再展开论述。

基于上述分析，在PSCAD／EMTDC 中搭建了直驱风电机组的仿真模型，并采用我国某实际风电场的1.5 MW 风电机组的实测数据与模型仿真结果进行了对比。风电机组参数如附录A 表A1所示，大功率输出（风电机组的有功功率P满足P>0.9 p.u.）和小功率输出（0.1 p.u≤P≤0.3 p.u.）时的对比结果分别如附录A 图A3、A4 所示。由图可知，在2 种工况下，所建立的模型均与实际风电机组具有一致的响应特性，从而验证了模型的有效性。

2 直驱风电机组的聚群特性

风电场多机等值的关键在于根据风电机组在不同工况下的暂态响应，识别出具有相似响应特性的机组，确定合理的分群指标。风电机组输出的暂态响应包括电压、电流、有功和无功功率，其中有功和无功功率是电压和电流的综合效果。由第1 节分析可知，风电机组在LVRT 过程的无功响应取决于控制策略、机端电压和故障前稳态值Q0（通常为0）。同一型号的直驱风电机组采用的控制策略相同，且场站内机组间电压比较接近［12］，因此根据其无功响应特性寻找分割点意义不大。而有功功率不仅取决于控制策略、机端电压，更主要的影响因素是风速。由于大型风电场中的风速分布通常较分散，从而导致机组间有功响应差异大，适宜以有功暂态响应为切入点，研究风电机组的聚群特性，寻找标志性的分割点进行机群划分。

当电压发生深度跌落时，风电机组的暂态响应波动较大，对系统造成的冲击强［21］，因此在进行大规模风电并网分析时，通常更关心电压深度跌落场景下的暂态响应。由第1 节的分析可知，当电压发生深度跌落时，故障清除后风电机组的有功功率和有功恢复速率会被限制，而在电压跌落程度较浅时，该限制可能不起作用，即当电压发生深度跌落时，与传统未考虑恢复过程时和电压跌落程度较浅时相比，风电机组的有功暂态响应存在明显差异。为此，本节分析直驱风电机组在电压发生深度跌落时，不同风速下的有功暂态响应特性。

设0.9 s 时风电机组出口发生短路故障，0.15 s后故障清除，风电机组在电压跌落至0.2 p.u.时的有功暂态响应如附录B 图B1 所示。图中每条曲线对应1 个风速下的有功响应，风速变化范围为切入风速4.5 m／s至切出风速23 m／s，变化间隔为0.1 m／s。由图B1 可知，电压跌落后运行于不同风速下风电机组的有功暂态响应呈现明显的聚群特性，下面将对这些聚群特性进行分析解释，并进行分割点的确定。由式（1）、（2）可知，电压跌落期间风电机组的有功功率Pfault可以表示为：

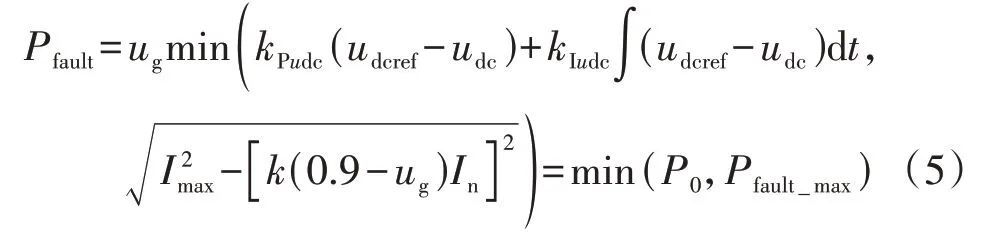
式中：Pfault_max为电压跌落期间风电机组能输出的最大有功功率，其表达式见式（6）。

由式（5）可知：当P0≤Pfault_max时，电压跌落期间风电机组仍具备有功调节能力，其输出的有功功率在稳态功率P0附近波动，不同风速的风电机组的有功功率不同，但暂态响应趋势相近，如附录B 图B1 中红色虚线所示；当P0>Pfault_max时，电压跌落期间风电机组失去有功调节能力，不同风速的风电机组输出的有功功率均处于该上限值Pfault_max，如附录B 图B1中蓝色实线和粉色点划线所示。由上述分析可知，当P0≤Pfault_max和P0>Pfault_max时，风电机组在电压跌落期间存在不同的有功响应，故可以Pfault_max为分割点对风电机组进行分群。由于稳态功率大于Pfault_max的风电机组在电压跌落期间的有功功率都相同，可以等值为1台等值机。下面对稳态功率满足P0≤Pfault_max的风电机组在电压跌落期间可以用1 台等值机进行表征的合理性进行说明。

假设风电场内有m台风电机组的稳态功率满足P0≤Pfault_max，电压跌落期间m台风电机组的有功可以表示为：

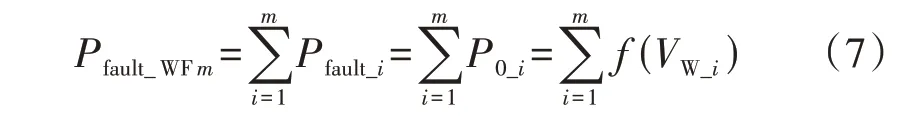
式中：P0_i为故障前第i台风电机组的稳态有功功率；Pfault_i为电压跌落期间第i台风电机组的有功功率；VW_i为第i台风电机组的风速；f为风电机组的风速与有功功率对应的函数关系。

设m台风电机组的单机等值模型的等效风速为Veq_m，则Veq_m可以表示为［5］：

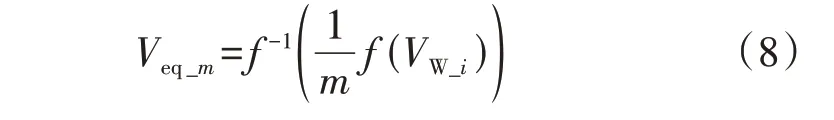
式中：f-1为风电机组的功率与风速对应的函数关系。将式（8）代入式（7）可得：

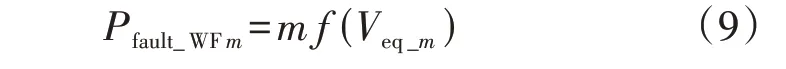
由式（9）可知，对于稳态功率满足P0≤Pfault_max的风电机组可以用1 台等值风速为Veq_m的等值机进行表征。

当电压发生深度跌落时，电压开始恢复后，稳态功率大于Pfault_max的风电机组的有功功率在经历了短时的暂态波动后开始上升。由式（3）、（4）可知：对于稳态功率满足Pfault_maxP0Pdelay_lim的风电机组，在电压开始恢复后可迅速将有功恢复至P0，无需斜率恢复过程，如附录B 图B1 中蓝色实线所示；对于稳态功率P0≥Pdelay_lim的风电机组，在电压恢复期间其有功功率恢复至Pdelay_lim，电压恢复后经历短暂的延时，随后以斜率rP逐步恢复至P0，如附录B 图B1 中粉色点划线所示。由上述分析可知，稳态功率满足Pfault_maxP0Pdelay_lim和P0≥Pdelay_lim的风电机组具有不同的有功恢复过程，因此可以Pdelay_lim为分割点对风电机组进行分群。其中，稳态功率满足Pfault_maxP0Pdelay_lim的风电机组可以等值为1 台等值机，该部分的合理性可参照式（7）—（9）进行说明；而P0≥Pdelay_lim的风电机组虽然具有相似的有功恢复过程，但所需恢复时间不一致，这部分的分割点无法直接从曲线形态上确定，将在3.2节进行讨论。

综上，根据对直驱风电机组在不同风速下的有功暂态响应进行分析，可以初步识别出2 个分割点Pfault_max和Pdelay_lim。

3 直驱风电场实用化分群方法

由第2 节的分析可知，在故障期间，稳态功率属于不同功率范围的风电机组，其有功响应曲线存在明显的聚群特性，若将风电场等值为单机，则无法计及不同机群间暂态响应的差异。在故障恢复过程中，虽然稳态功率不同的风电机组具有相近的有功暂态响应，但所需恢复时间不一致，若将风电场等值为单机，则无法计及风电机组有功恢复时间的差异。因此，本节分别探讨直驱风电场在故障期间和故障恢复过程的分群方法，最后形成适用于电压发生深度跌落时直驱风电场的实用化分群方法。

3.1 故障期间分群方法

为验证第2 节识别出的2 个功率分割点Pfault_max和Pdelay_lim的有效性，基于PSCAD／EMTDC 仿真平台搭建了如图1 所示的66×1.5 MW 的直驱风电场仿真系统，对比风电场单机等值模型，以Pfault_max和Pdelay_lim这2 个分割点形成的三机等值模型与详细模型的暂态响应。图1 中风电场集电线路参数设为电阻0.12 Ω／km，电感0.001 05 H／km，风电机组参数同附录A 表A1，等值风电机组的参数采用文献［22］的容量加权法计算，集电线路等值参数按照文献［22］的方法计算。值得说明的是，运行于额定风速以上的风电机组的有功暂态响应几乎一致，因此选取风速分散分布于额定风速以下（即4.5 m／s至12 m／s之间）的风速场景进行仿真实验，风速分布如图2 所示。电压跌落至0.2 p.u.时等值效果如附录B 图B2所示，其中三机等值模型的具体分群结果如附录B表B1所示。

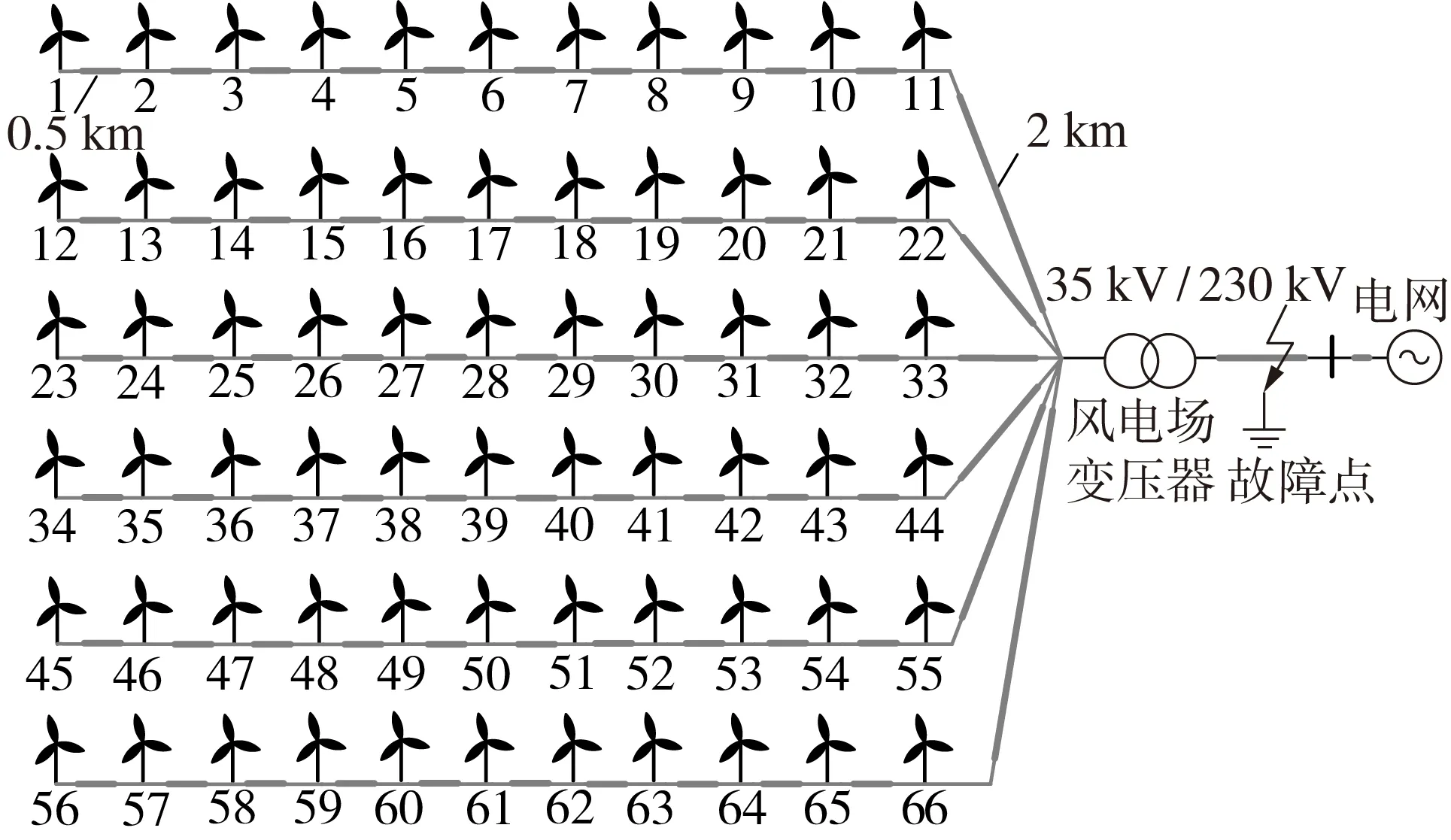
图1 直驱风电场仿真系统示意图Fig.1 Schematic diagram of simulation system of direct-driven wind farm

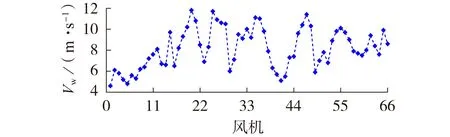
图2 风电场风速分布Fig.2 Wind speed distribution of wind farm

由图B2 可知，采用分割点Pfault_max进行分群可以消除故障期间的等值误差，采用分割点Pdelay_lim进行分群可以消除故障清除后有功恢复起点的误差，从而验证了分割点Pfault_max和Pdelay_lim的有效性。但考虑到Pfault_max是关于残压ug的函数，其值随ug变化而变化，对于不同的电压跌落场景该分割点不固定，工程实用性不好，而对于某一型号的风电机组Pdelay_lim是确定的。此外，本文进一步研究发现，当电压发生深度跌落时，故障期间仅采用Pdelay_lim为分割点与采用Pfault_max和Pdelay_lim这2 个分割点时的等值效果十分接近，因此分割点Pfault_max存在的意义不大，采用Pdelay_lim进行分群即可，具体分析如下。

假设风电场内有m台风电机组的稳态功率满足P0≤Pfault_max，n台风电机组的稳态功率满足Pfault_maxP0Pdelay_lim。对于这m+n台风电机组，仅采用Pdelay_lim进行分群时可以等值为1台等值机，设等值风速为VWeq_1；采用Pfault_max和Pdelay_lim这2 个分割点时，可等值为2 台等值机，设2 台等值机的等值风速分别为VWeq_21和VWeq_22。仅采用Pdelay_lim进行分群时，m+n台风电机组在故障期间的有功功率可以表示为：

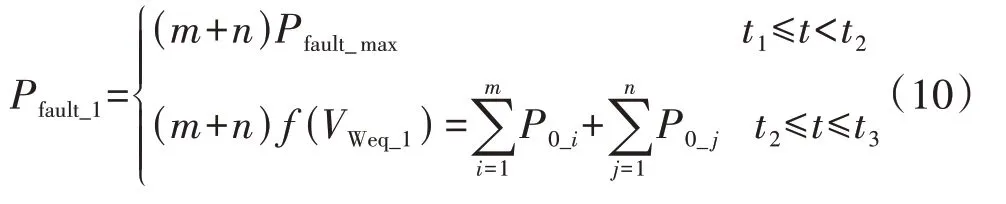
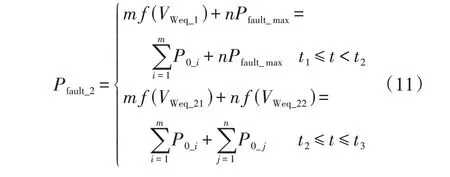
采用Pfault_max和Pdelay_lim这2 个分割点分群时，m+n台风电机组在故障期间的有功功率可以表示为：对比式（10）、（11）可知，相比于采用Pfault_max和Pdelay_lim在2 个分割点的分群方案，仅采用Pdelay_lim进行分群时所引起的误差可以表示为：

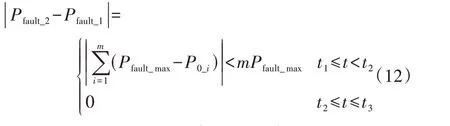
由式（12）可知，故障期间舍弃分割点Pfault_max，仅采用Pdelay_lim进行分群所引起的误差只存在于电压跌落期间［t1，t2），误差的大小与Pfault_max密切相关。电压发生深度跌落时Pfault_max通常很小，以k=1.5、Imax=1.2 p.u.为例，当电压跌落至0 或0.1 p.u.时，Pfault_max=0，此时式（12）的误差为0，即仅采用Pdelay_lim为分割点与采用Pfault_max、Pdelay_lim这2 个分割点时的分群结果完全一致，不会引起误差；当电压跌落至0.2、0.3 p.u.时，Pfault_max分别为0.11 p.u.和0.23 p.u.，由于Pfault_max很小，P0_i与Pfault_max的差值会更小，仅采用Pdelay_lim进行分群引起的电压跌落期间有功功率的误差在实际应用中可以忽略，据此确定了本文所提分群等值方法的第1 个分割点Pdelay_lim。

为了验证上述分析的合理性，本文设置不同的电压跌落场景，对比风电场三机等值模型（分割点为Pfault_max和Pdelay_lim）、两机等值模型（分割点为Pdelay_lim）与详细模型的暂态响应，结果见附录B 图B3，其中三机等值模型和两机等值模型的具体分群结果分别见附录B表B2、B3。仿真中风速分布同图2。

由图B3 可知，在故障期间：当电压跌落至0 和0.1 p.u.时，三机和两机等值模型的有功暂态响应均与详细模型一致；当电压跌落至0.2 p.u.和0.3 p.u.时，三机等值模型的有功暂态响应与详细模型一致，而两机等值模型的等值效果略差于三机等值模型，但总体误差并不大，等值效果在可接受的范围内。同时，由于故障持续时间通常较短（约0.15～0.2 s），相比于后续约为秒级的恢复过程，该部分误差在实际工程应用中完全可以忽略。综上，在电压发生深度跌落时分割点Pfault_max存在的必要性不大，以Pdelay_lim为分割点即可满足精度要求。

3.2 故障恢复过程分群方法

由图B3 可知，在故障期间以Pdelay_lim为分割点的两机等值模型与详细模型的有功暂态响应十分接近，但在故障清除后二者的有功恢复曲线存在明显差异，产生误差的原因可分析如下。

将风电机组按照其稳态功率升序排列，根据式（4），故障恢复过程风电场详细模型有功响应PWF_rec为：

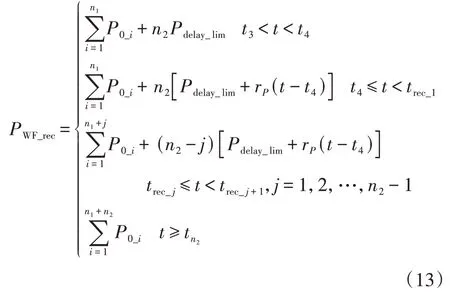
式中：n1为稳态有功小于Pdelay_lim（即不需要斜率恢复）的风电机组数量；n2为稳态有功大于等于Pdelay_lim（即需要斜率恢复）的风电机组数量；trec_j为第j台风电机组的有功恢复至稳态值的时刻。

故障恢复过程两机等值模型有功响应PEQ_rec为：

式中：trec_eq为等值模型的有功恢复至稳态值的时刻。

根据式（13）、（14）可以得出详细模型和两机等值模型在恢复过程的有功响应，如图3 所示。对比式（13）和式（14）可知，两机等值模型与详细模型的有功恢复误差来源于式（15）所示不等关系式。

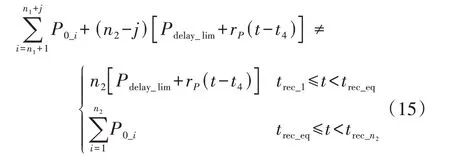
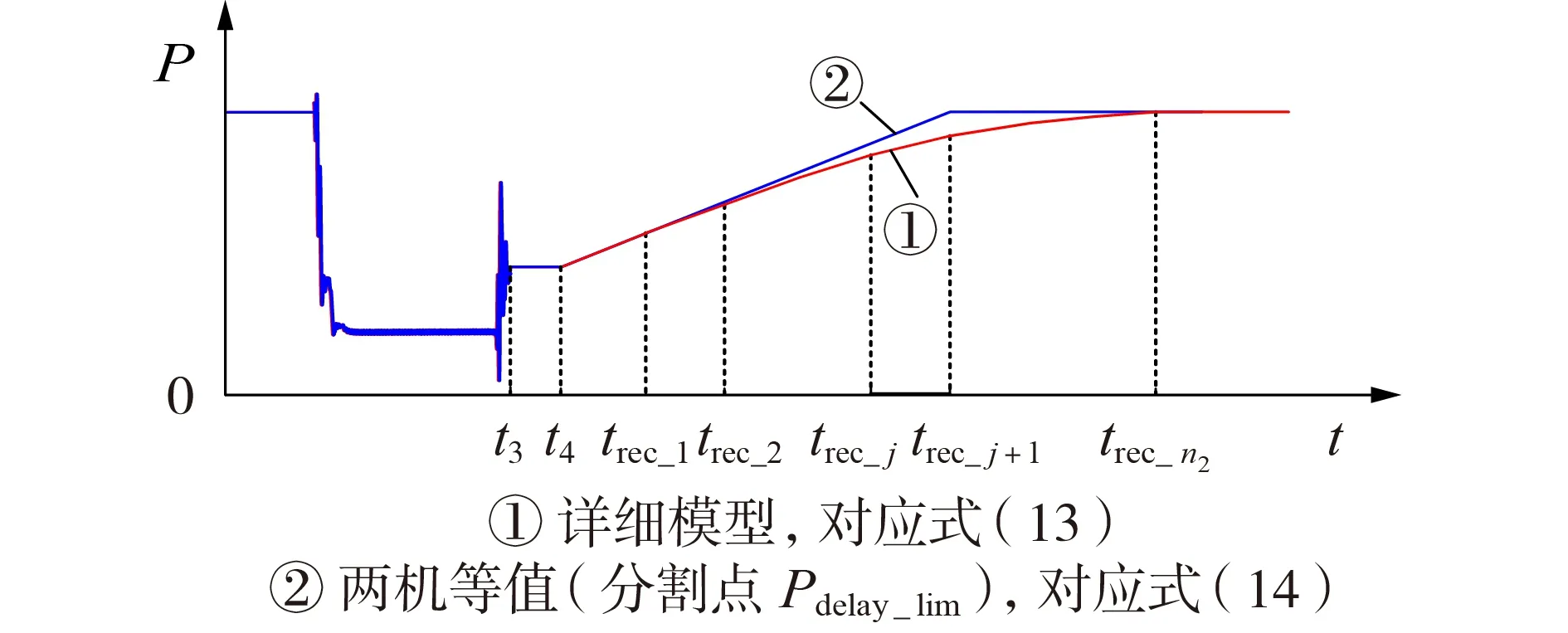
图3 详细模型与等值模型的有功恢复过程示意图Fig.3 Schematic diagram of active power recovery process for detailed model and equivalent model

由式（15）和图3 可知，不同功率的风电机组（需要斜率恢复的）所需的恢复时间trec_j不一致，风电场详细模型的恢复速率在trec_j时刻发生改变，而等值模型的斜率始终为n2rP。为了提高等值模型的精度，需要对存在斜率恢复过程的风电机组进一步分群。考虑到分群数增加虽然会在一定程度上提高等值精度，但也会降低计算效率，而本文提出的直驱风电场等值建模方法侧重于工程实用性，分群方法的关键在于兼顾精度的条件下将机组分成尽可能少的群，所以考虑将斜率恢复的风电机组分成两群。文献［22］采用仿真实验的方法，将斜率恢复的风电机组依次以每台机组的风速为分割点，对其两机等值方案进行了遍历，发现以所有斜率恢复的风电机组的平均功率Pramp_avg为分割点进行分群的等值模型具有较高的等值精度，并通过多组实际风速数据进行了验证。基于这一结论，将附录B 图B3 的仿真算例以Pramp_avg为分割点（这里为0.86 MW）对斜率恢复的风电机组再次分群，构成三机等值模型，其等值效果如附录B 图B4 所示，具体分群结果如附录B 表B4 所示。由图可知，等值模型和详细模型的有功响应基本一致。所以，将Pramp_avg确定为所提分群等值方法的第2个分割点。

3.3 实用化分群方案

综上，本文提出一种直驱风电场实用化等值方法，依据LVRT 过程的有功暂态响应的差异性，从实用化的角度将风电场内的风电机组划分为三群，如图4 所示。其中：第一群为故障前功率属于［0，Pdelay_lim］的风电机组，该群风电机组的稳态功率很小，电压跌落期间功率在其稳态值附近波动或达到上限值Pfault_max，电压开始恢复后风电机组的有功功率迅速恢复至稳态值；第二群为故障前功率属于（Pdelay_lim，Pramp_avg］的风电机组，该群风电机组的稳态功率较小，电压跌落期间功率达到上限值Pfault_max，电压开始恢复后先恢复至Pdelay_lim，在经过了tdelay_P的延时后以斜率rP逐渐恢复，所需恢复时间相对较短；第三群为故障前功率大于Pramp_avg的风电机组，该群风电机组的稳态功率较大，电压跌落期间功率同样达到上限值Pfault_max，电压开始恢复后先恢复至Pdelay_lim，在经过了tdelay_P的延时后以斜率rP逐渐恢复，所需恢复时间相对较长。

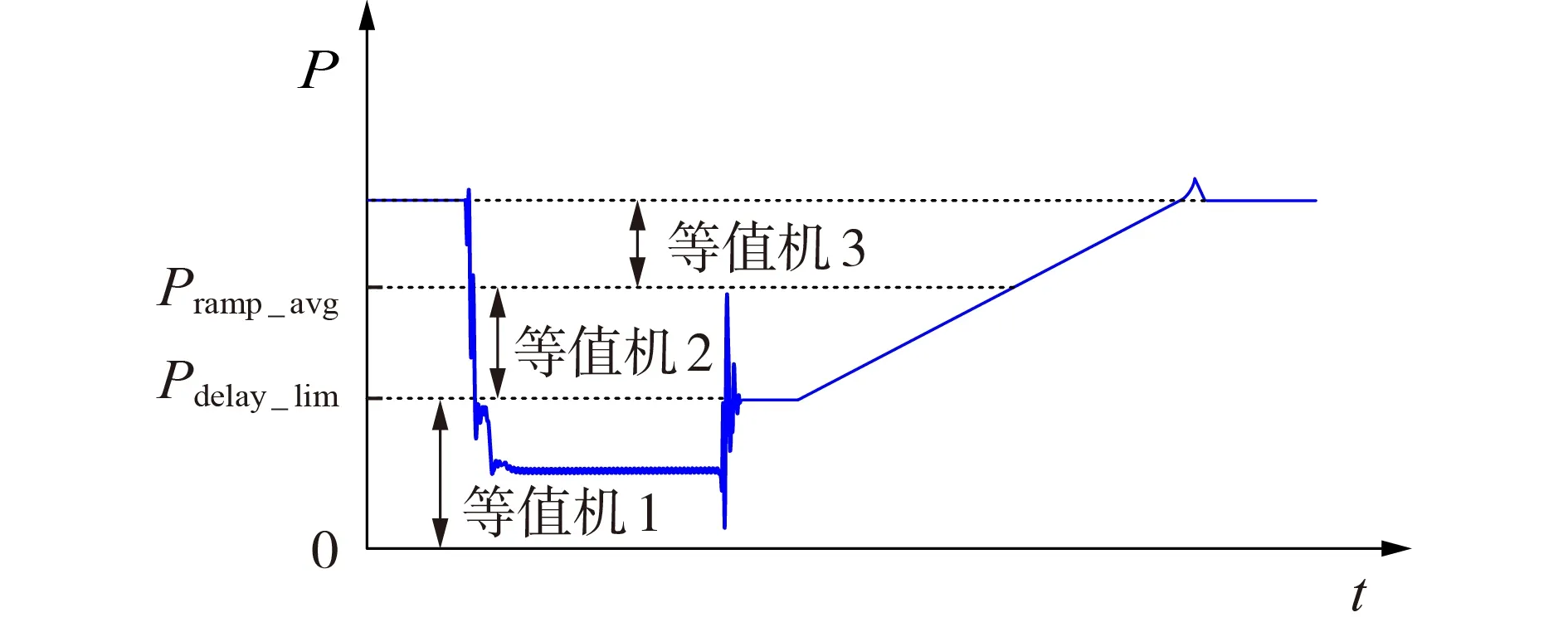
图4 直驱风电场实用化三机等值策略示意图Fig.4 Schematic diagram of practical three-machine equivalent scheme of direct-driven wind farm

4 仿真验证

本节基于图1 所示的风电场仿真系统，对所提出的直驱风电场实用化三机等值模型进行验证。

4.1 不同风速场景下等值模型的适应性

为验证本文提出的等值方法在不同风速场景下的有效性，从风电场实际风速数据中随机选取30 组进行仿真实验，对比提出的等值模型，单机等值模型，文献［10］、［19］提出的多机等值模型与详细模型的响应特性。值得说明的是，为支撑电网电压，风电机组在故障期间优先提供无功功率，但文献［10］提出的方法并未考虑这一因素。为保证对比的公平性，将文献［10］的等值模型进行调整使其在故障期间提供无功支撑。

仿真算例采用的风速数据如附录C 图C1 所示。0.9 s 时风电场出口处发生三相短路接地故障，电压跌落至0，1.05 s 时故障清除。选取风速分布较均匀的第1组和风速分布较分散的第10组的等值效果进行展示，分别如图5、6 所示（图中ug为标幺值，后同）。第1 组和第10 组对应的功率分割点分别为0.45、0.91 MW和0.45、1.38 MW。

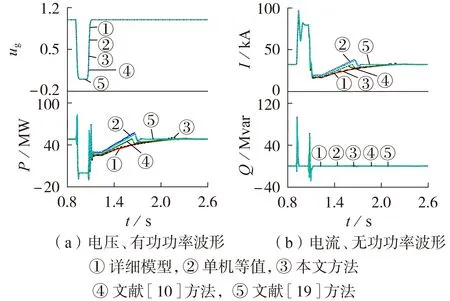
图5 风电场出口三相短路时第1组风速下的等值效果Fig.5 Equivalent effects of 1st group wind speed for three-phase short circuit at wind farm’s port

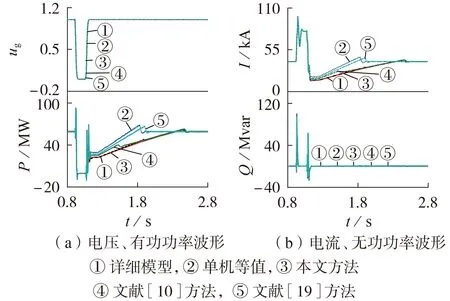
图6 风电场出口三相短路时第10组风速下的等值效果Fig.6 Equivalent effects of 10th group wind speed for three-phase short circuit at wind farm’s port

由图5、6 可知，故障期间风电场单机等值模型及文献［10］、［19］和本文提出的多机等值模型均与详细模型具有一致的响应特性。但在故障清除后的恢复过程，文献［10］、［19］的等值模型与详细模型的有功恢复特性存在明显的差异，这是因为文献［10］、［19］均未考虑恢复过程，所提多机等值方法在分群时仅计及风电机组在故障期间的差异，无法对风电场详细模型在故障清除后的响应特性进行准确表征。而本文提出的三机等值模型在不同风速场景下都可以准确地反映风电场出口的电压、电流、有功和无功功率的响应特性，相比于单机等值模型、文献［10］、［19］的多机等值模型，等值精度均得到显著提高。因此，本文提出的分群策略可以适用于不同的风速场景。

4.2 不同电压跌落场景下等值模型的适应性

为验证本文提出的等值方法在不同电压跌落场景下的有效性，在风电场出口的故障点设置不同的电压跌落，对附录C 图C1 中30 组风速场景重新进行仿真。附录C 图C2、C3 分别对比了本文提出的等值模型和单机等值模型以及文献［10］、［19］提出的多机等值模型与详细模型在第10 组风速下，电压跌落至0.2 p.u.和0.3 p.u.时的等值效果。由图可知：当电压跌落至0.2 p.u.时，风电场单机等值模型及文献［10］、［19］和本文提出的三机等值模型在故障期间均与详细模型具有一致的响应特性；当电压跌落至0.3 p.u.时，文献［10］、［19］和本文提出的等值模型在故障期间具有与详细模型一致的响应特性，但单机等值模型等值效果较差；在故障清除后的恢复过程中，文献［10］、［19］提出的等值模型的有功恢复响应虽优于单机等值模型，但仍与详细模型存在明显的差异，而本文提出的三机等值模型在不同电压跌落场景下都与详细模型具有相似的故障响应特性。因此，当电压跌落程度变化时，相比于单机等值模型和文献［10］、［19］提出的多机等值模型，本文提出的等值方法等值精度更高，提出的分群策略可以适用于不同程度的电压跌落场景。

4.3 不同无功恢复策略下等值模型的适应性

4.1、4.2 节的仿真算例中无功功率在电压恢复后直接恢复至故障前的稳态值，为验证所提等值方法在不同无功恢复策略下的有效性，设置风电机组采用无功斜率恢复策略，对附录C图C1中30组风速场景重新进行仿真。附录C 图C4、C5 分别给出了第1 组和第10 组风速下电压跌落至0.2 p.u.时的等值效果。由图可知，故障期间风电机组提供无功支撑，故障清除后无功功率保持在0 左右，500 ms 后切换回正常运行模式。由于切换后无功功率小于故障前稳态值，风电机组以斜率逐步完成无功功率的恢复。采用无功斜率恢复策略时，本文提出的三机等值模型仍与详细模型具有一致的故障响应特性。因此，提出的分群策略可以适用于无功斜率恢复的场景。

5 结论

本文提出了计及LVRT 特性的直驱风电场实用化等值方法。该方法依据LVRT 过程中风电机组有功暂态响应的差异性，将直驱风电场内的风电机组划分为三群。通过多组实测风速数据，验证了所提等值方法对不同风况、不同电压跌落深度的适应性。所提方法物理意义清晰、分群指标易获取、无需使用复杂的聚类算法，具有较强的工程实用价值。

附录见本刊网络版（http：//www.epae.cn）。