HPM视角下平方差公式的教学设计——从参数角度

◎杨 辉 欧阳露露 方颖钰

(1.深圳大学师范学院,广东 深圳 518061;2.深圳市盐田区梅沙双语学校,广东 深圳 518000;3.怀化市鹤城区黄岩学校,湖南 怀化 418000;4.深圳大学数学与统计学院,广东 深圳 518061)

1 问题提出

平方差公式是初中数学“代数”领域中重要的一个基础知识，是代数式的变形、化简和计算的重要依据，对于后续内容，如因式分解和分式化简有着非常重要的基石作用.

在教材编排上，国内北师大版、人教版、苏教版教材都是将平方差公式放在整式的乘法后面，更具体地，是放在多项式乘多项式之后，从而将平方差公式的学习逻辑简单地“解释”为多项式乘以多项式的“特殊”形式.

科学的论证要以事实资料为基础，借助理论依据或者证据来支持自己的主张，并通过逻辑推理形成最终结论.在数学教育的目标方面，Wilkins认为学生应该做到以下几点：(1)掌握数学内容的知识点；(2)拥有数学推理能力；(3)认同数学的实用性和社会影响力；(4)理解数学的现状和历史发展；(5)对数学有积极的态度.在平方差公式这一内容上，国内教材在(1)(4)两点方面都做得不足，都没有向学生呈现平方差公式出现的原因.而这一点对于知识的底层框架来说，至关重要.

这一问题的答案，可以从数学史的发展中找到.平方差公式衍生于求解二元二次方程组的问题，而非特殊形式的多项式乘以多项式.古巴比伦数学泥版上记录了二元问题：

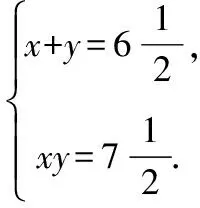
此外，公元3世纪，数学家丢番图在《算术》一书中，也有类似解法：已知两数和为20，积为96，求这两个数.设一个数为10+t，另一个数为10-t，t>0,于是有(10+t)(10-t)=96.所以t=2，则一个数为12，另一个数为8.

吴现荣等人利用公元3世纪中国数学家赵爽的“面积割补法”史料来引入平方差公式.学生先从图形表征的角度发现(a+b)(a-b)=a2-b2，再从符号表征层面熟知平方差公式.这样的教学设计与苏教版教材内容编排类似，只是多了一个数学史的“帽子”.但是，以图形表征入手，还是没有呈现出平方差公式出现的原因，会让学生“错误认为”平方差公式是在面积重构中偶然被发现的.吴梅龙从情境表征入手，以重构的方式来呈现数学史在平方差公式中的应用，所创设的情景为：某房地产开发商打算在上海黄金地段购买一块土地建造商品房，现有两块价格相同的土地，一块是边长为a(a>5)米的正方形土地，另一块是一边长为(a+5)米，另一边长为(a-5)米的长方形土地.假如你是开发商，你会如何选择?这种引入方式能够让学生经历知识的形成与应用过程，激发学生学习的兴趣和信心，但依旧没有体现出平方差公式的由来.

目前，关于平方差公式直接发生的教学研究，尚未有人涉及.本文将直接从平方差公式的数学史出发，从参数的角度进行教学设计，以期让学生掌握平方差公式的由来和意义.不管是古巴比伦数学泥版上的问题，还是丢番图的问题，都引入了新的中间变量t，这个t后来被称为参数.如果教师能够很好地在平方差公式教学中引入参数，那么学生就可以直接了解平方差公式学习的本质和意义.

2 参数在数学教学中的应用

通过检索文献，研究者们将参数的概念渗透到了初中数学和小学数学中.尽管只是理解层面，但是为本文从参数角度出发，设计平方差公式的教学提供了理论支撑.

孙海燕发现参数在小学数学解题中可以起到“搭桥”作用.如参数在“比”中的应用：已知甲校的学生是乙校学生人数的40%，甲校的女生人数是甲校学生人数的30%，乙校的男生人数是乙校学生人数的42%，求两校的女生总数与两校学生总数比.设乙校学生人数为参数a，找出数量关系，问题便迎刃而解.胡健认为参数沟通了已知量和未知量之间的关系，为建立数学模型解决问题创造了条件.张培炜通过参数在初中数学函数解题中的妙用，阐述了掌握参数的解题方法可以有效提高学生的数学思维能力.

3 从参数角度基于HPM视角下的平方差公式教学设计

以北师大版教材为例，进行平方差公式的教学设计.

3.1 已有学习基础

在学习平方差公式之前，学生已经学习了“多项式乘以多项式”.此外，经过小学“一元一次方程”的学习，学生会设未知数来求解问题.并且，通过“用字母表示数”这一章节的学习，学生能够理解字母可以表示任意数.最后，在几何图形的学习中，学生能够利用“割补法”来求解图形面积.

3.2 关于平方差公式的教材内容

平方差公式是多项式运算中的一个重要公式.学生通过教材中几个具体的题目，能利用多项式乘以多项式发现规律，并能对规律进行证明.在引出平方差公式之后，教材通过拼图游戏为平方差公式作几何解释，从而使学生对此公式有一个直观认识.

3.3 教学设计

3.3.1 教学目标

依据马复等人关于义务教育的教学要求，在平方差公式章节，需要完成的教学目标有：(1)经历探索平方差公式的过程，进一步发展符号意识和推理能力；(2)会推导平方差公式，并能运用公式进行简单的计算和推理；(3)了解平方差公式的几何背景，发展几何直观核心素养.

3.3.2 教学设计与实施

(1)参数导入

教师用PPT展示一道小学四年级的题目：

问题：动物园饲养员给三群猴子分花生，如果只分给第一群，则每只猴子可得12粒；如果只分给第二群，则每只猴子可得15粒；如果只分给第三群，则每只猴子可得20粒.若平均分给全体猴子，每只猴子可得多少粒花生？

师：这是一道小学四年级的题目，已经是七年级学生的你们来思考一下，是否有一个合乎逻辑的解题过程？

经过5分钟左右的思考，部分学生会有思路：12，15，20的最小公倍数为60，60为花生的总数，再用60分别除以12，15和20，得出三群猴子的数量分别为5，4和3.所以若平均分给全体猴子，每只猴子可以得到60÷(5+4+3)=5(粒).

师：为什么一定要用最小公倍数作为花生的总数？如果60可以，那么60的倍数120，180是否也可以呢？

生：有道理，好像也行.如果是120，用120分别除以12，15和20，得出三群猴子的数量分别为10，8和6.所以若平均分给全体猴子，每只猴子可以得到120÷(10+8+6)=5(粒).答案还是一样的，那么60的倍数都可以.

师：如果仅用60的倍数来作为花生数，会出现一个问题，每个同学用的花生总数不一样，但是答案都是对的.那有没有一种解法，可以统一这些解题方法呢？

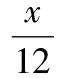
生：x没必要求出来，x起到一个桥梁的作用.

师：(总结)很好！x没有必要求出.x作为辅助变量，即参数，出现在题目中，是沟通数量之间的一个桥梁.

(2)平方差公式的导入

了解了参数在均分思想中的作用后，学生对于平方差公式的构造有了基本的知识基础.随后，教师用PPT展示公元3世纪遇到的分地问题：

问题：公元3世纪，在河流一侧有一个部落，一天在河水退去后，面对肥沃的土地，部落首领需要给族人分地.分得的土地要保证是一整块，否则会给耕种带来麻烦.一块土地的长宽和为20米，面积为96平方米.这块土地的长和宽分别是多少？

师：大家不要用特殊值法去尝试，用方程知识来解决，可以想想刚刚学到的“参数在均分思想中的应用”.

学生思考了一段时间.

生：设长为x米，则宽为(20-x)米.由题意知x(20-x)=96，即x2-20x+96=0.但是这个方程，我不会求解呀！

师：公元3世纪的人们也遇到了跟大家一样的问题.无法求解一元二次方程，难道就不分地了吗？

师：聪明的部落首领想到了分地的方法.长和宽的和为20，当平均分配给两个数时，为10和10.在两个10的基础之上，一个多分配x，那么另一个就要少分配x.因此，可以设长为(10+x)米，宽为(10-x)米.则(10+x)(10-x)=96，即100-10x+10x-x2=96，100-x2=96，x=2.所以这块土地的长为12米，宽为8米.

师：请大家想一想，这里的x的作用是什么？

生：是参数的作用.

师：对！当引入参数后，我们就可以轻易地解决这个问题.那么大家看看这里的(10+x)(10-x)=100-x2是什么公式？

生：是平方差公式.

师：现在大家思考一下，平方差公式出现的意义是什么？

生：用来解决一元二次方程的问题.

师：非常好！认识到平方差公式的本质之后，我们就可以进一步学习平方差公式的各种证明方式了.

(3)平方差公式的表征

教师用PPT展示平方差公式表征的三种形式.

A.图形表征

(1)如下图，一个边长为a的正方形，在左下角剪下边长为b的小正方形，其阴影部分的面积为________.

(2)如果沿虚线剪开，重新拼凑，则重新拼凑出来的图形的面积是________.

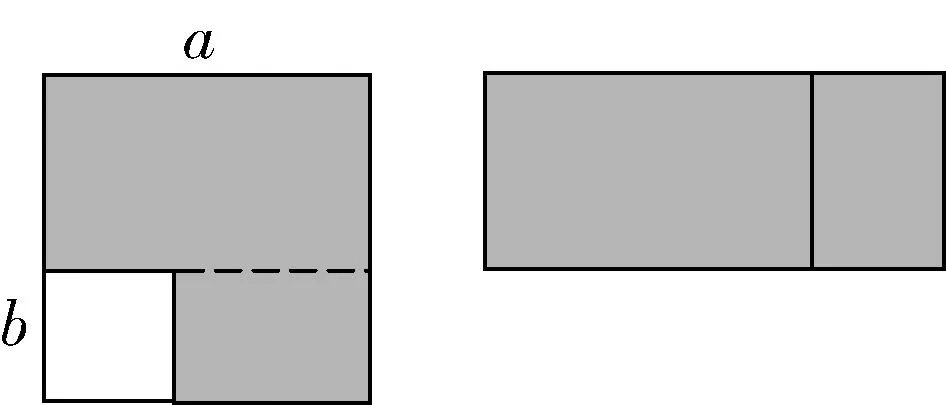
师：大家将完成这两个填空题.

生：第(1)问的答案是a2-b2，第(2)问的答案是(a+b)(a-b).

师：阴影部分的图形被重新拼接，那么图形本身的面积是否发生改变？

生：没有改变.

师：第(1)问和第(2)问的答案相同，即(a+b)(a-b)=a2-b2.这是从几何的角度来表征平方差公式.

B.模型表征

用“□”和“○”来表示单项式或多项式，帮助学生理解平方差公式里的a和b的真正含义，从而使学生更准确地理解平方差公式.

教师设置如下的填空练习：

(□+○)(□-○)=________.

当□、○表示单项式时，

(2a2+3b)(2a2-3b)=________________;

当□、○中含有多项式时，

[(2a-b)+5c2][(2a-b)-5c2]=________.

C.文字表征

师：基于这堂课的学习，请你用一句话来总结平方差公式的形式.

生：两数的平方之差，等于两数的和乘以两数的差.

(4)公式辨析

教师用PPT展示问题，让两位同学来判断对错，并对错的题目进行订正.

①(a+b)(b-a)=ab-ba=0；

②(-5x-3)(5x-3)=25x2-9；

③(4x+3b)(4x-3b)=16x2-9；

④(x-2a+1)(x+2a-1)=x2-4a2.

教师解答：

①错误，左边的(a+b)做一个简单的移项即可，答案是b2-a2.

②错误，左边的(-5x-3)提一个负号出来，变成-(5x+3)，答案是-(25x2-9)=-25x2+9.

③错误，答案是16x2-9b2.

④错误，将(2a-1)看成一个整体，答案是x2-(2a-1)2=x2-4a2+4a-1.

(5)公式应用

教师用PPT展示平方差公式的应用题型.

例1计算59.8×60.2.

例2从前有一个狡猾的农林主，把一片边长为a的正方形土地租给王老汉.第二年，他对王老汉说：“我把这块地的一组对边减少5米，另一组对边增加5米，继续租给你，租金不变，你觉得怎么样？”王老汉觉得没吃亏，就同意了.回到家中，王老汉把这个事说给邻居们听，邻居们都说他吃亏了，你觉得呢？

解答

例1原式=(60-0.2)×(60+0.2)=602-0.22=3600-0.04=3599.96.

例2第一年的土地面积为a2,第二年的土地面积为(a+5)(a-5)=a2-25.显然第一年的土地面积比第二年多，所以王老汉吃亏了.

(6)小结

通过提问的方式，让学生总结本节课所学的内容.

问题一，平方差公式出现的原因是什么？

问题二，说一说平方差公式的形式.

问题三，平方差公式里的a和b可以表示什么？

问题四，谈一谈平方差公式的应用.