让“准备课”体现其真正的价值
———“周长与面积”单元整体教学的再实践与新思考
文徐 宾
一、直面困惑,探索整合之需
在小学“图形与几何”板块的学习中,“面积”与“周长”是两个非常重要的概念。但在实际教学中,老师们都会发现对于这两个概念不管在概念形成时还是在应用阶段,学生均特别容易混淆。首先让我们聚焦以下两个案例:
【案例1】
下图的长方形分成了两个部分,哪个部分的面积大,哪个部分的周长长?

【案例2】
小明用同样长的两根铁丝围成了甲乙两个图形,比较它们的面积,那么( )。
A.甲比乙大 B.乙比甲大
C.一样大 D.无法比较

我们发现在三年级下册学完面积之后让学生做案例1 这道题,班级里仍然有很多学生认为“面积大的图形周长也长”。案例2选自张丹教授《小学数学教学策略》这本书。这是一道小学生数学学业质量评价测试题,在当年抽样测试随机抽取的1664 份样本中,有37.7%的学生认为周长一样的图形面积也相等。以上两个案例反映学生对周长和面积概念的模糊不清,混淆严重。
学生为什么会经常出现这样的错误呢?笔者认为主要有以下原因:
原因一:学生对面积的直觉早于周长,容易受到已有认知经验的负迁移。
学生看到实物时,“边”和“面”往往是一起看到的,并且容易从面积的角度来判断周长,错误地认为面积越大的图形周长越长。
原因二:人教版教材分块式编排特点,周长与面积的教学时间跨度较大。
教材将认识周长、周长的计算与解决问题放在了三年级上册,将认识面积、面积的计算与解决问题放在三年级下册,中间时间跨度较大,把周长和面积割裂开来,弱化了它们之间的联系。
基于以上分析,笔者开始思考是否可以尝试做一些调整,让周长与面积更早的相遇呢?此时特级教师吴正宪老师和潘小明老师两堂课燃起了笔者的探究之火。吴老师在认识周长一课中,创造性地引入有关面的内容,让学生初步感受“面与边”的区别。潘老师则是全课始终围绕周长与面积的关系,在一次次猜测分析比较中打破学生固定思维。同时,笔者通过翻看不同版本的教材,意外地发现,浙教版的教材在三年级上册将认识周长和认识面积放在一个单元里教学,三年级下册再进行长方形和正方形的周长和面积的计算教学,这无疑给笔者对整合研究带来了信心。
二、重组内容,探求整合之法
如何让周长与面积更早的相遇呢?又如何让学生在“对比”中初步分清线与面这两个基本概念呢?笔者对“周长和面积”单元内容进行重组整合,在人教版编排的基础上设想:
1.打破时间阻隔,建立周长与面积的密切联系。
2.微调重组融合,提前建构周长与面积的概念。
3.强化对比辨析,集中分块式教学计算及运用。
我们采用“位移、合并、新增”等方式,创造性地将教学内容进行重组,突显整合中的“合”。
三移:将面积前置,与周长对比教学;将长方形和正方形的周长计算后置,与面积的计算对比教学;将周长解决问题后置,与面积解决问题对比教学;三次对比,让学生在比较中对周长和面积这两个概念有了更好地辨析,强化意义构建。
三合:将周长面积概念的练习、计算的练习以及解决问题的练习进行合并,在练习中强化对比,真正理解概念的本质特征。
一增:新增一节准备课——《大小与长短》,让学生基于已有生活经验,在比较中初步分清楚线与面这两个概念,知道图形的一周是有长短的,面是有大小的,并能用直观的方式来描述比较。

三、课堂实践,凸显整合价值
1.合理定位教学目标。
目标一:能借助具体情境正确指认边框线和玻璃面分别指的是照片哪一部分。淡化周长与面积的概念,直观、整体地认识面和线。
目标二:经历用数一数、移一移等方法比较玻璃面的大小和边框线的长短的过程。明确数玻璃大小和边框线长短的方法是不一样的,玻璃面的大小是一块一块地数,边框线的长度是一段一段地数。
目标三:沟通同一个物体中玻璃大小与边框线长短之间的联系,发现“玻璃面大的边框线不一定长,玻璃面小的边框线不一定短”。打破思维定势,在争辩、说理的过程中,体会到线与面既有联系又有区别,感悟线与面的本质。
2.实践寻求教学策略。
【策略一】借助情境,激活经验,初步感知。
(1)情境引入。
师:学校招募兴趣小组成员,8 名同学被航模小组选中,现在老师把这些大小相同的小正方形照片,组合起来挂在墙上。为了美观,在四周围上边框线,表面装上玻璃。

(2)感知线面。
师:边框线在哪里?谁来指一指?玻璃装在哪里?谁来摸一摸?
(3)巩固线面。
师:还有9 个同学被学校的合唱小组录取了,老师把他们的照片也组合起来,拼成了一个正方形,我们也来装饰一下。边框线、玻璃分别在哪里?

本环节,利用将航模小组和合唱小组学员照片进行组合装饰的情境,唤醒了学生的生活经验。通过正确指认边框线和玻璃面分别指的是照片哪一部分,使学生明白围边框和装玻璃问题解决的是生活中线的长短和面的大小的问题,为今后学习周长和面积的概念作铺垫。
【策略二】借助冲突,利用经验,数出本质。
(1)比较引发冲突。
师:比一比,哪一组照片需要的玻璃面更大?哪一组照片需要的边框线更长?

生:合唱小组玻璃面大,边框线肯定是合唱小组的长。
生:我不同意。合唱小组玻璃面大,边框线长度相等。
(2)数玻璃面大小。
生:合唱组的玻璃面更大。航模组有8 个小正方形,合唱组有9个小正方形。
(3)数边框线长短。
采注比是生产井的排液速度与注入井的注汽速度的比值。在油层物性、流体特征和几何参数确定以后,稠油蒸汽驱存在一个最佳的采注比。数值模拟分别预测了采注比为1、1.1、1.2和1.3时油藏采收率的变化。在采注比提高到1.2时,采收率最大,但当采注比将继续增大到1.3后,采收率不再增加。因此推荐采注比为1.2。
师:那边框线到底哪一组更长呢?同桌合作研究。
生:可以数边框线的段数。航模组的边框线包含了12 段,合唱组边框线也包含了12 段,两组边框线一样长。
(4)分清数法不同。
师:数边框线和数玻璃面有什么不一样吗?
生:比玻璃面大小数的是小正方形的块数,比边框线长短数的是边线的段数。

(5)打破思维定势。
师:一开始很多同学们认为玻璃面大的边框线也长。通过研究,我们发现边框线却是相等的。看来,玻璃面大的边框线不一定长。
在本环节教学中,首先,通过“比较面大小和线长短”的活动设计,使学生体会数边框线长短和数玻璃面大小的方法是不一样的,数面是一块一块数的,数线是一段一段数的,在数的过程中明晰面与线的本质。其次,让学生经历体会了测量的基本方法:先要统一单位,再用统一的单位去累加。最后,通过争辩、说理,初步改变了原有的认为面大线一定长的思维定势。
【策略三】游戏拼图,调整经验,改变定势。
(1)情境设疑。
师:在合唱小组中拿走一张照片,玻璃面和边框线会发生什么变化?

(2)合作探究。
师:拿走一张照片,玻璃面变小了,我们一眼就可以看出来。那边框线呢?我们一起来研究。
(3)反馈说理。
作品一:拿走角落上任意一块,边框线不变。
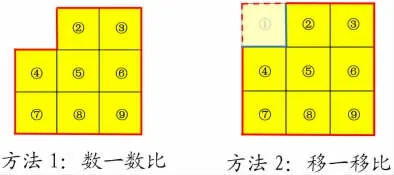
师:还可以拿去几号照片边框线的长度也是不变的?
生:拿走角落上任意一块,玻璃面变小了,边框线不变。
作品二:拿走边上中间的一块,边框线变长。
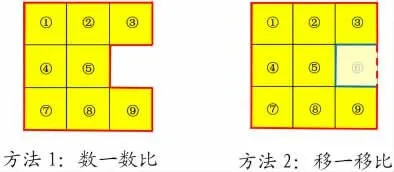
师:还可以拿去几号照片边框线的长度也变长了?
生:只要拿走边上中间的一块,玻璃面变小了,边框线反而变长。
(4)再次打破思维定势。
师:拿走了一张照片,玻璃面变小了,而边框线不一定变短。
这一环节,创设了“拿走一块,玻璃面和边框线有什么变化?”这个挑战性的数学问题,引领学生“小组探究”活动。学生的探究欲望被激发,不同层次的学生基于对面与线的理解,想到了不同的解决策略,从而进一步巩固并分清了面和线的本质。通过“变与不变”的活动设计,使学生进一步体会到周长与面积既有联系又有区别,进一步改变了思维定势。
【策略四】开放练习,积累经验,发展思维。
(1)选一选。
玻璃面和边框线会发生怎样的变化?(2)创意小达人。
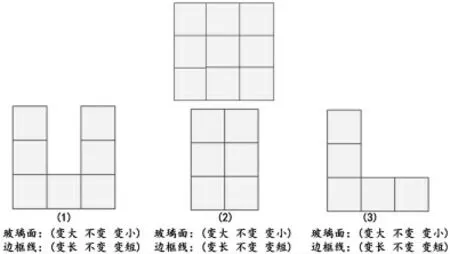
把四张照片拼接成自己喜欢的形状,围上边框线,怎样拼边框线最长?怎样拼边框线最短?

(3)有效凸显整合价值。
基于本堂课的目标定位以及教学策略,笔者认为《大小与长短》这节课作为周长与面积的准备课,有很大的价值,它为学生后续学习进行了铺垫。比如通过指一指边框线、摸一摸玻璃面这个环节渗透周长与面积的概念;通过数一数、移一移比玻璃面和边框线渗透周长与面积的计算;通过数的活动渗透周长是单位长度的累加和面积是单位面积的累加;通过三次面和线变化的感悟渗透周长与面积解决问题中面与线的关系。这样的设计,真正让“准备课”体现出真正的价值。

