任意边界条件下双模量矩形薄板的弯曲
曹彩芹, 宋永超
(西安建筑科技大学 理学院,西安 710055)
1 引 言
玻璃和陶瓷等材料具有拉压弹性模量不同的力学特性,使用这种材料的薄板称为双模量板。双模量板的解析求解一直受到国内外相关学者的广泛关注。
文献[1]用康托洛维奇法和伽辽金法计算四边固支的双模量矩形板的弯曲,但是该文献只针对四边固支的矩形板,对于其他边界条件的板,没有给出合理的解法。文献[2]用Kantorovich及Galerkin联合法研究双模量板的弯曲,但是该方法对于不同的边界条件需要重新假定挠度函数,计算较为不便。文献[3,4]分别分析了双模量矩形板和圆板的弯曲变形。以上文献都将坐标轴取在板的中性面上,但是在求解中性面的位置的过程中,没有充分考虑中性面上的正应力和切应力都为零的条件。
此外,文献[5]采用改进的渐进损伤分析方法预测了双模量复合材料层合结构的承载极限。文献[6]分析了拉压弹性模量差异对泡沫铝夹芯板三点弯曲模拟的影响。文献[7]研究了编织复合材料的双模量本构关系和细观模型。文献[8]用Chebyshev函数研究了双模量梁变形时的解析解。文献[9]基于牛顿-拉夫逊理论进行了拉压不同模量问题的数值求解。文献[10]用能量法研究了双模量大挠度圆板的轴对称弯曲。文献[11,12]也对双模量构件进行了研究。文献[13]提出了带补充项的双重正弦傅里叶级数通解,该通解可以适用于任意边界条件的矩形薄板。
本文改进了板的中性面与板上表面的距离公式,经过分析可知本文方法是合理的。将文献[13]提出的通解应用到双模量矩形薄板中,求解了任意边界条件下双模量矩形薄板弯曲时的挠度函数。并将本文解与有限元解相比较,验证了本文方法的可靠性。
2 双模量矩形薄板的中性面位置
由于双模量板的拉压弹性模量不同,板的中性面位置不在板的中面处。为了将坐标轴取在中性面上,首先需要求出板的中性面位置。
将双模量板等效为两个各向同性小矩形板组成的层合板,如图1所示,两个小矩形板的交界处即为板的中性面。

图1 两个各向同性小矩形板组成的层合板
板的应力可由挠度函数表示为
(1)
(2)
(3)
式中i=1,2为第i个小矩形板;x,y和z为板上某一点的坐标;Ei,μi和Gx y i分别为第i个小矩形板的弹性模量、泊松比和切变模量,w为板的挠度函数,一般为w(x,y)的形式;σx i,σy i和τx y i分别为第i个小矩形板x方向的正应力、y方向的正应力和切应力。
在薄板全厚度上,应力σx,σy和τx y各自的代数和均为0,由此可以求出板的中性面位置。
(4)
(5)
(6)
式中h0为板的中性面与板上表面的距离,h为板的总厚度。
将式(1,2)分别代入式(4,5)得
(7)
(8)
式(7,8)相加得
(9)
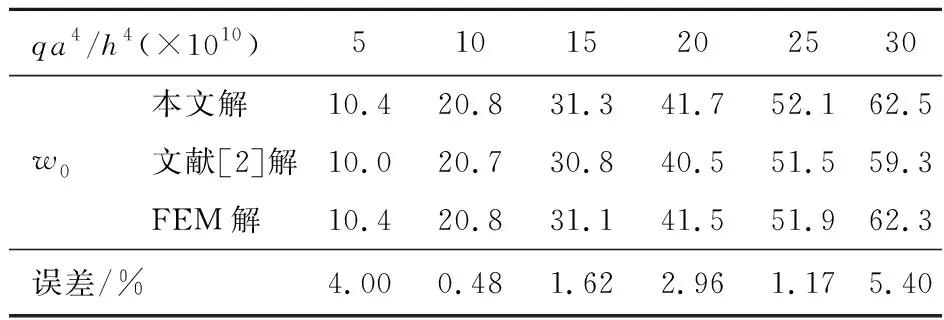
解式(9),并考虑h0 (10) 式(7)减去式(8)得 (11) 解式(11),得到第二个满足式(7,8)的解 (12) 将式(3)代入式(6),并解之,得到的结果与式(12)相同。 由于板的中性面唯一,由正应力与剪应力求得的中性面位置应该重合。因此,本文采用式(12)的值作为中性面与板上表面的距离。 文献[1-4]采用式(10)的值作为中性面距离板上表面的距离,其原因在于式(4,5)联立后本应有两组解,即式(10,12),文献[1-4]只求出一组解,而且没有考虑式(6)的解。因此本文的方法更合理。 由文献[14]及式(1~3)知,板的内力可表示为 (13) (14) (15) (16) (17) (18) (19) (20) 由文献[14]知,矩形薄板的弯曲平衡方程为 (21) 式中q为板受到的横向荷载。 将式(13~15)代入式(21),得到双模量矩形薄板的弯曲控制方程 (22) 参考文献[15],以x=0的边与x=0,y=0处的点A为例。 4.2.1 简支边的边界条件 若简支边发生支座沉降而产生挠度ξ,且板边受到分布弯矩M作用,则该边的边界条件可以表述为(w)x = 0=ξ, (Mx)x = 0=M。 4.2.2 固定边的边界条件 若该边发生支座沉降而产生挠度ξ与转角θ,则该边的边界条件可以表述为(w)x = 0=ξ,(∂w/∂x)x = 0=θ。 4.2.3 自由边的边界条件 4.2.4 角点的边界条件 若该角点为自由边交点且无支座,当该点受集中荷载P作用时,角点条件可以表述为2(Mx y)A=P。若该角点有支座且支座沉降产生挠度ξ,角点条件可以表述为(w)A=ξ。 本文采用严宗达[13]提出的带补充项的双重正弦傅里叶级数通解,形式如下, (23) 式中wo o,wa o,wo b,wa b,An,Bn,Cm,Dm,En,Fn,Gm,Hm和bm n均为待定系数;a和b分别为板的长和宽。 参考文献[2],选取四边简支双模量矩形薄板,板长a=2 m,板宽b=2 m,板厚h=0.1 m;压缩区弹性模量为E1=30.38 GPa,泊松比μ1=0.35;拉伸区弹性模量为E2=16.17 GPa, 泊松比μ2=0.19。板受横向均布荷载作用,荷载大小为q。采用本文方法,解得板的中性面与板的上表面的距离为h0=0.0473 m。计算板中点处的挠度值w0,并与文献[2]解及有限单元法(FEM)的结果比较,给出本文解与文献[2]解的误差。结果列入表1。 表1 板中点处的挠度值w0(单位:mm) 由表1可知,本文重新推导中性面位置并将双模量板等效为两个各向同性小矩形板组成的层合板的方法是有效的。且与文献[2]相比,本文方法求得的结果更精确。 仍采用6.1节中双模量矩形薄板,板厚h=0.02 m;板受横向均布荷载作用且q=625 Pa。改变板的边界条件,计算板的最大挠度值wmax。结果列入表2。 对比表2的结果,本文方法在计算任意边界条件下的双模量矩形薄板时,得出的结果与有限元解接近。误差均在5%以内,符合工程精度要求。 误差分析,本文方法未考虑剪切变形的影响,且采用直法线假定,在挠度较大处存在较大误差。 (1) 本文给出的双模量矩形薄板中性面的位置的计算方法充分考虑了应力σx,σy和τx y的分布,使得在该中性面满足应力σx,σy和τx y都为0,且全截面上应力的代数和也都为0。 (2) 将双模量板等效为两个各向同性小矩形板组成的层合板来计算,从结果看,该等效方法是合理的。 (3) 本文方法适用于任意边界条件的双模量矩形薄板,而且该方法不需要叠加,也不需要针对不同的边界条件重新构造通解。 (4) 本文的误差来自于薄板小挠度弯曲理论计算假定,当板厚度较大或者板的挠度较大时,该理论已经不再适用。 表2 各种边界条件下双模量矩形薄板的最大挠度值wmax(单位:mm)3 板的内力



4 控制方程和边界条件
4.1 双模量矩形薄板的弯曲控制方程
4.2 双模量矩形薄板的边界条件
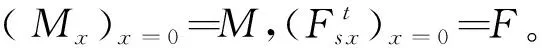
5 通解的引入
6 算例分析
6.1 四边简支双模量矩形薄板的弯曲分析
6.2 任意边界条件下双模量矩形薄板的弯曲分析
7 结 论


