基于离散元的杆件断裂全过程数值模拟
齐 念, 郑开启
(1.南京交通职业技术学院,南京 211188;2.南京林业大学 土木工程学院,南京 210037)
1 引 言
结构在服役期内会遭遇多种荷载和作用,尤其是在强震、强风以及爆炸等极端荷载作用下,组成结构的部分杆件会进入塑性,甚至会出现损伤和裂纹;随着荷载作用的不断加强或持续,微细裂纹不断扩展,当裂纹贯通杆件全截面时,构件发生断裂,最终引起结构部分或完全倒塌[1]。整个过程中,杆件经历了弹性小变形、塑性开展、损伤累积直至最后断裂。采用数值方法对破坏全过程进行模拟,需实时模拟结构的几何大变形、材料非线性以及构件断裂失效不连续等问题,这对现有的数值计算方法是一个巨大的挑战[2,3]。如Lynn等[4]通过对有限元方法进行修正,将自适应变换积分高斯技术引入到有限元方法中,处理单元的断裂和接触问题,对飞机冲撞世贸大楼倒塌破坏问题进行了模拟分析;Zhang等[5]将粘结力模型和拓扑数据结构优化引入有限元,用以模拟混凝土结构中的动力破坏和裂纹扩展问题。但有限元法模拟裂纹扩展问题时需不断进行网格重划分,使得计算非常复杂并且效率较低。
与有限元法的理论基础不同,离散元法DEM属于非连续介质数值方法,现已成为研究岩石岩土、颗粒散粒体以及混凝土等材料非线性力学行为的常用方法[6]。由于不要求满足位移连续和变形协调条件,因此DEM能方便地应用于各类材料非连续、非均匀以及结构大变形和断裂破坏等复杂过程及其失效机理的研究。如Potyondy[7]基于应力腐蚀理论提出了平行黏结应力腐蚀模型,以模拟应力或水溶液等对岩石胶结的应力腐蚀作用;杨升等[8]基于PFC3D颗粒流程序,对砂土在剪切过程中的体积变化及力学行为进行了宏细观分析;刘志林等[9]利用颗粒流离散元方法建立了一种含骨料、砂浆和过渡层的混凝土细观力学模型,对弹丸侵彻混凝土进行了研究。为了拓展离散元法的应用范围,在前期研究工作中,本文以颗粒离散元为基础,提出了一种适于杆系结构分析的DEM计算模型,并成功地应用于平面框架结构、大跨空间网格结构的弹性、动静力响应分析和几何大变形分析[10-12]。与有限元法不同,构建框架结构的DEM模型时,是将梁柱等杆件离散为刚性单元集合体,单元与单元之间采用特定的接触弹簧连接,每个单元的运动遵循牛顿第二定律。从方法的本身属性而言,DEM处理断裂等不连续问题在行为模式上更加直观,因此较有限元法更具优势。
本文基于已有研究,提出了一种适于结构弹塑性分析的DEM纤维梁模型,然后构建了杆件断裂模拟算法,并自编了构件断裂计算程序;最后将其应用于悬臂梁结构和单层网壳振动台倒塌试验两个算例,对杆件的弹性和弹塑性直至断裂全过程进行模拟,通过数值分析验证该方法的正确性和适用性。
2 DEM纤维梁模型
在杆系结构的弹性DEM方法中,颗粒球元之间的接触粘结看作是一根弹性梁,两球心的距离即为弹性梁的长度L,且采用构件实际截面的几何物理参数计算各弹簧接触刚度系数[12]。弹塑性分析时,借鉴纤维模型的研究思路,将两相邻颗粒球元之间的接触粘结用分布式弹簧进行等效,分布弹簧看作是梁截面的若干根纤维,每一根弹簧对映着梁单元上的一根纤维,如图1所示。
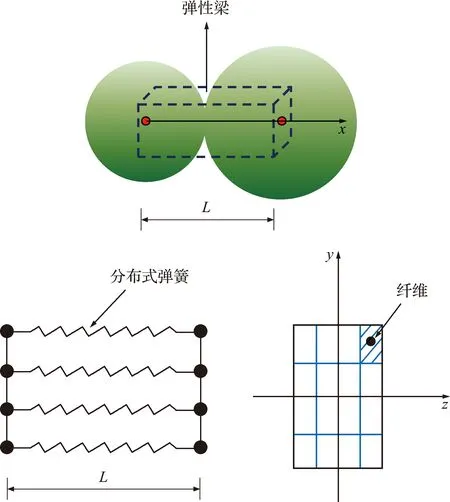
图1 DEM纤维梁模型
通过定义弹簧(纤维)的本构关系描述截面的变形与受力,进而可确定颗粒球元之间的粘结弹塑性接触本构方程。假设每根纤维处于单向受力状态,以平面问题为例,则梁单元截面上任一点处的应变为
ε=εN+εMz
(1)
式中εN为轴力产生的应变,εMz为绕z轴弯曲产生的应变。
εMz=κzyi
(2)
式中κz为绕z轴弯曲引起的曲率,yi为第i个纤维到截面中和轴的距离。
DEM方法采用增量形式对运动方程进行求解。在一个时步Δt内,首先可求得相邻球元A和球元B的法向相对位移增量ΔUn以及相对转角增量Δθ,则时步Δt内纤维的应变增量以及曲率增量可表示为
(3)
式中ΔεN为轴向应变增量,Δκz为绕z轴弯曲引起的曲率增量。
将式(3)代入式(1,2),可得
Δε=ΔεN+Δκzyi
(4)
由式(4)可知,已知截面各纤维的应变增量,根据材料的弹塑性本构方程、加卸载准则和增量理论,即可进一步求得截面纤维的应力增量 ,其具体实现过程与通常的弹塑性有限元分析完全一致[13],不再赘述。
为了满足计算精度并节省计算量,将构件截面离散为若干个纤维块,再将弹簧置于纤维块的高斯积分点处。通过对截面所有纤维进行应力分析,可得到截面的接触内力增量为
(5)
式中Ai为第i个纤维的面积,ΔFn为截面法向接触力增量,ΔMz为绕z轴引起的接触力矩增量。
上述DEM纤维梁模型,能充分考虑截面塑性的发展过程。对于破坏前塑性阶段不可忽略的材料或结构而言,模拟分析结果更加精细化和更接近于工程实际。
3 构件断裂模拟算法及实现


(6)

如前文所述,构件截面由多根弹簧组成,那么当某一时刻截面上所有弹簧均已发生断裂,定义为全截面开裂,断裂模式则表现为两相邻球元脱离分开;初始时刻,球元之间的粘结处于完好状态。以图2(a)所示的悬臂梁结构DEM模型(离散为7个球元)为例,在力P作用下,靠近固定端处截面所受的内力最大,故球元1和球元3之间的粘结梁截面应变(应力)最先满足断裂准则,在某一时刻该部位首先发生断裂,球元3与球元1发生脱开,接触粘结消失,如图2(b)所示。
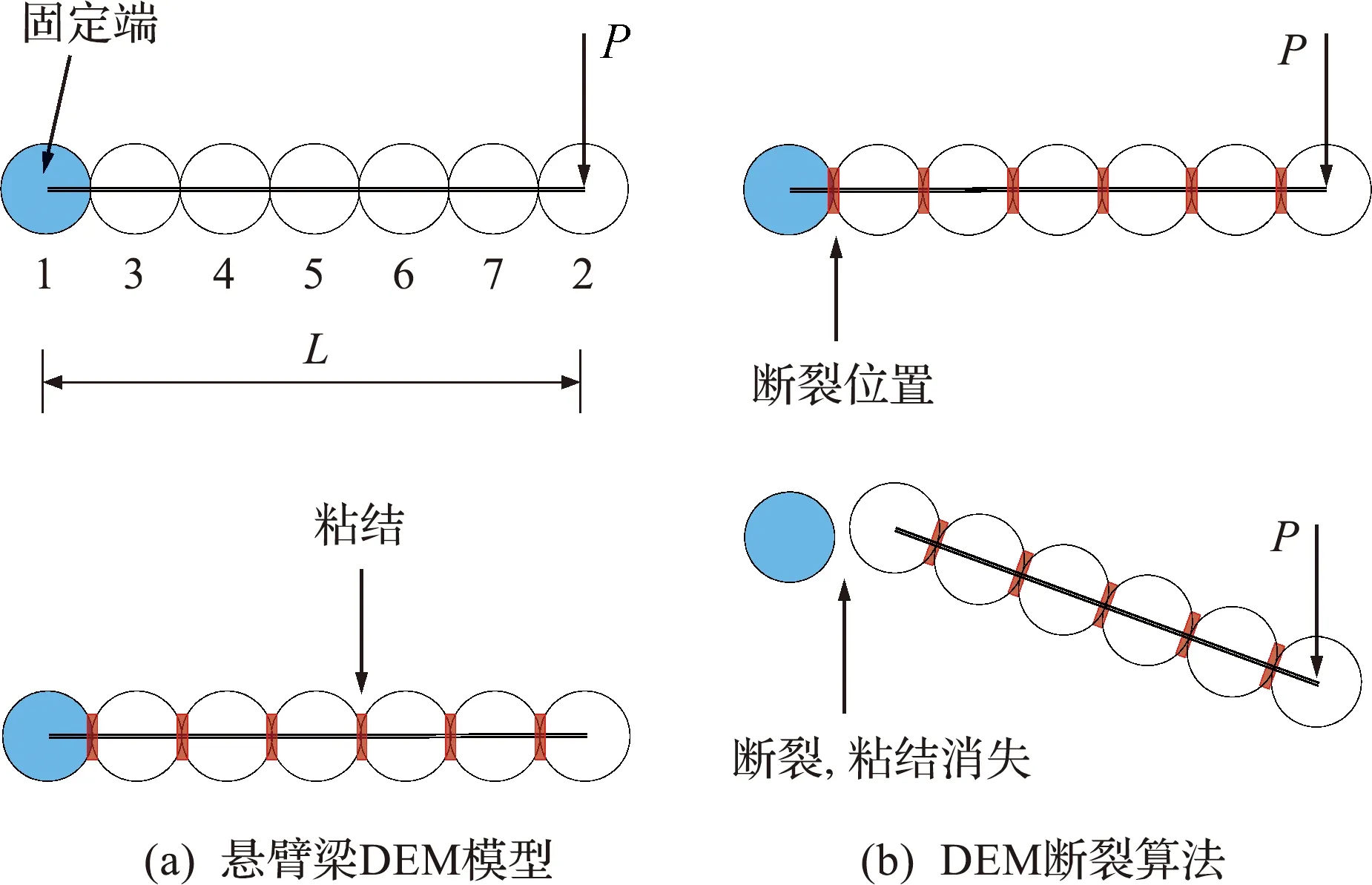
图2 悬臂梁DEM断裂过程模拟
当球元之间的粘结发生断裂和消失后,需要将该截面的接触力Fn和接触力矩Mz设为零,从而使球元在下一个时步的计算中获得内力和外力的更新。此外,断裂过程具体模拟时,本文不考虑球元自身的破裂,同时假定构件在断裂前后球元的总数量保持不变。
根据上述理论,基于Fortran语言开发了DEM纤维梁模型弹性-弹塑性以及构件断裂分析计算程序。
4 悬臂梁算例


图3 自由端受集中力作用的悬臂梁
用DEM方法模拟时,将悬臂梁离散为11个球元,球元粘结数量为10,计算时步Δt取为1.0×10-4s。当力P取值较大时,该悬臂梁会因为几何非线性和材料非线性产生极端大变形,采用考虑截面塑性开展的纤维梁模型更能真实地模拟这种力学行为。
采用纤维梁模型时,如图4所示,沿截面高度方向划分为10个纤维块,每个纤维块上有两根弹簧并置于高斯积分点上。
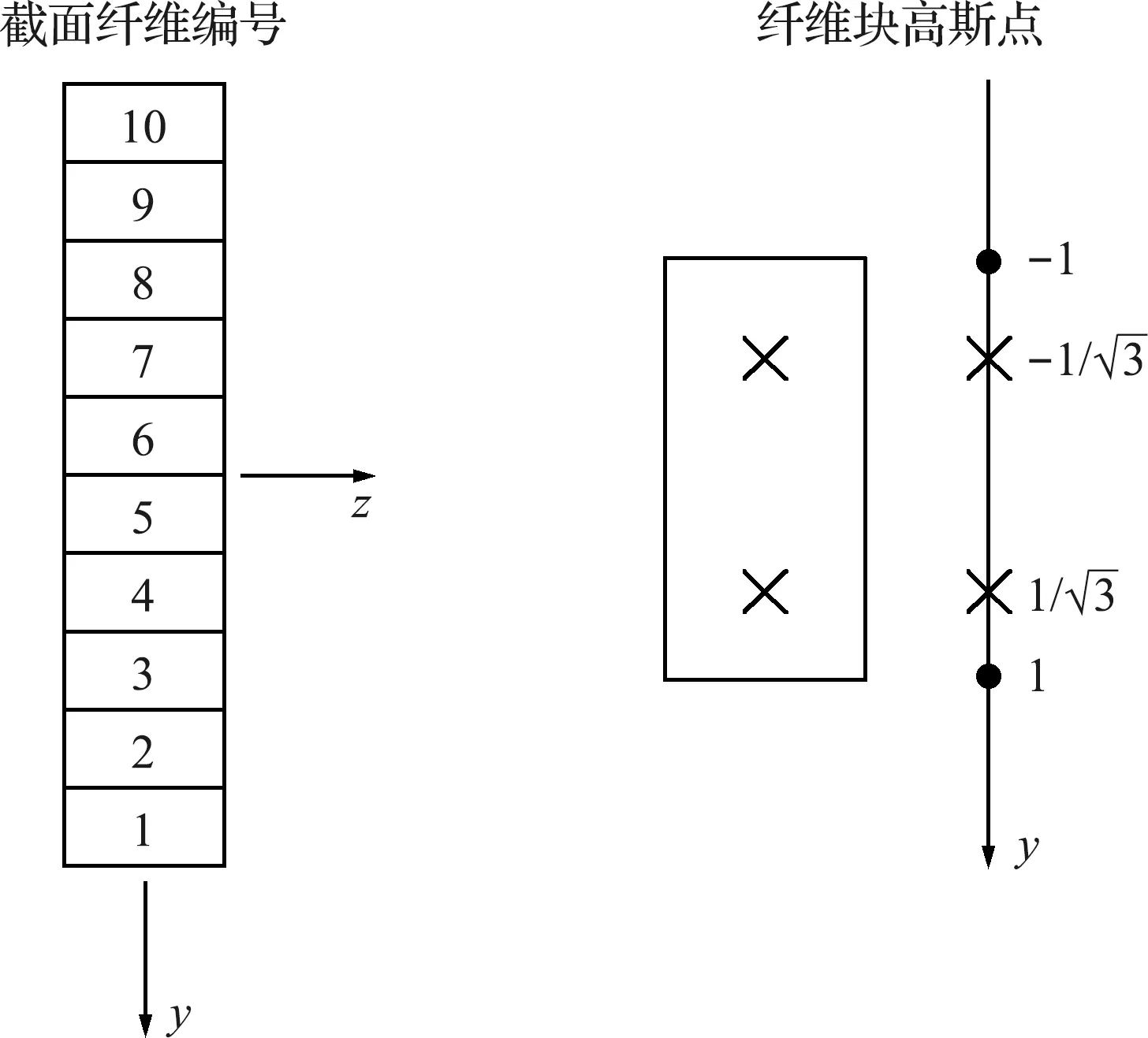
图4 截面纤维划分及高斯点
构件断裂模拟时,采用式(6)作为断裂准则,取纤维的极限应变εu=0.05。计算过程中每个加载时步均需对截面各纤维进行断裂判别,当全截面发生断裂后,该截面处的粘结消失,将球元之间的接触力和接触力矩设为零并移除外力,从而实现杆件断裂过程的数值模拟。
图5为不同时刻下悬臂梁的变形图。当外力P=130.6 N时,认为悬臂梁固定端全截面发生断裂(仅剩1根纤维未失效),随后撤去自由端外力且设定断裂不再发生,悬臂梁脱离固定支座发生自由运动(图5(a))。不考虑断裂时,许多学者对该算例进行了研究,如Yang等[14]用有限元法对该算例进行了弹塑性大变形分析。图5(b)为不考虑断裂时悬臂梁在不同外力值下的变形图,随着荷载的增加梁自由端位移不断增大,同时梁的变形程度也愈加显著,可以看出,本文方法与文献结果吻合较好,验证了该方法的正确性和有效性。

图5 不同时刻下悬臂梁的变形
图6为梁固定端处截面纤维在不同荷载值下的逐渐开裂过程。可以看出,当力P=99.4 N时,截面最外层纤维(即1号和10号)首先发生断裂;随着荷载值的增加,截面塑性区域逐渐扩大,9号、2号、8号和3号等纤维由于达到极限应变相继失效,截面破坏程度逐渐加剧;截面由外到内逐渐开裂,最终当外力P达到130.6 N时,截面除5号纤维外其他纤维已全部失效,在此基础上荷载稍有增加即发生了全截面断裂。
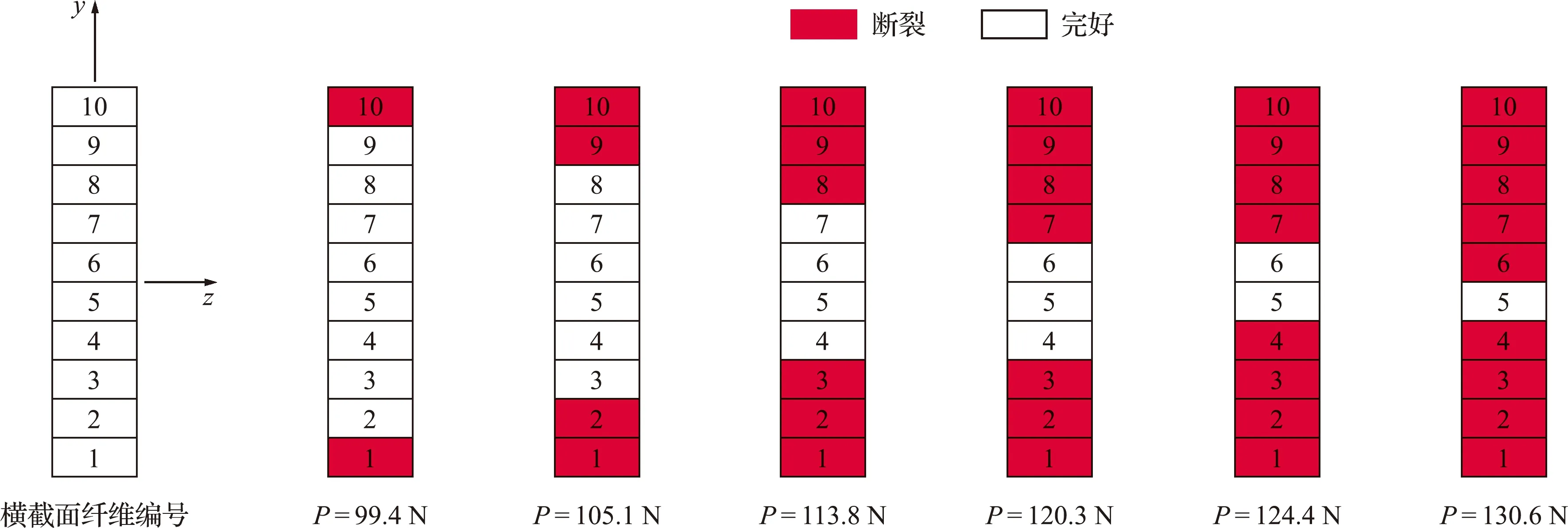
图6 梁固定端处截面纤维开裂过程
图7为梁固定端处截面纤维在断裂过程中截面抵抗弯矩与曲率的变化关系曲线。当外力P从0逐渐增加到99.4 N之前,截面各纤维均处于完好状态,截面抵抗弯矩随曲率增加而不断增大,其中当截面部分纤维发生屈服后,由于刚度下降导致曲线斜率减缓;当P=99.4 N时,由于截面最外层纤维发生开裂失效,截面抵抗弯矩由最高点(452.3 Nm)急剧下降到257.4 Nm,然后又线性递增直至下一个纤维开裂;当截面纤维逐个发生开裂并退出工作后,纤维应力设置为0,截面抵抗弯矩不断减小并最终趋于0。

图7 梁固定端处截面抵抗弯矩与曲率关系曲线
图8是梁固定端相接触的球元速度时程曲线。在截面未开裂之前,因缓慢加载,球元的速度几乎为零,可认为是静态的;而一旦全截面发生了开裂,球元速度瞬间急剧增大,然后随着脱离体的自由运动不断发生动态变化。上述计算分析过程验证了本文所提杆件断裂模拟算法的有效性和合理性。

图8 梁固定端处球元速度时程曲线
5 单层网壳结构算例验证与分析
为验证本文方法在大跨空间网格结构中的适用性,以文献[15]开展的单层球面网壳模型结构振动台倒塌试验为例进行对比分析。文献中设计了3个K6型单层球壳结构缩尺模型,跨度均为7.5 m,矢跨比均为1/2。选取其中的模型3作为研究对象,试验模型的几何物理参数及地震波加载工况等参见文献。本文用DEM模拟时,将网壳的各根杆件根据其长度分别离散成5~8个球元,离散元模型如图9所示,共有球元4315个,球元粘结4698个。试验模型所用的杆件均为不锈钢钢管,截面均为Φ14×0.6。采用纤维梁模型时,其截面纤维划分如图10所示。模拟焊缝处断裂时各钢管纤维对应的极限应力取为560 MPa[16]。

图9 单层球壳离散元模型
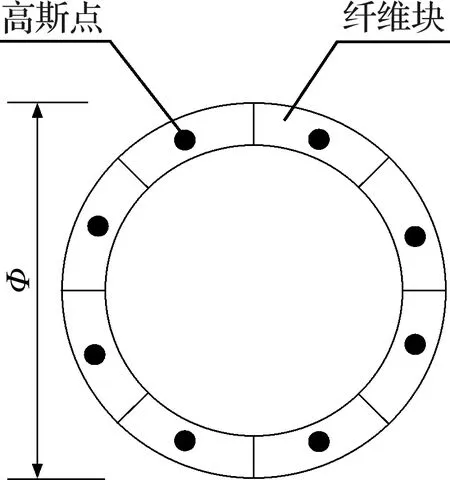
图10 圆管截面纤维划分
图11为单层球壳模型振动台试验破坏现象,当输入峰值加速度PGA达到2108 gal时,模型从下至上第1圈和第2圈的斜杆发生弯曲并且数量持续增多,部分杆件与球节点处发生断裂(图11(a));继续增大PGA至2268 gal时,第1圈和第2圈部分杆件和球节点完全与结构脱离,网壳模型发生整体倒塌,如图11(b)所示。

图11 试验模型破坏现象
图12为本文方法模拟得到的网壳试验模型破坏过程数值仿真结果,与振动台试验现象[15]比较一致。可以看出,当PGA小于1200 gal时,结构整体基本未发生变形;当PGA提高至1600 gal时,模型底部第1圈少量斜杆首先发生弯曲(图12(a));当PGA达到1800 gal时,由于部分焊缝先满足断裂准则,该部位斜杆与焊接球节点断开(图12(b)),但数量较少;随着PGA的继续增大,模型从下至上第1圈和第2圈的斜杆相继发生弯曲,当PGA增大至2100 gal时,支座附近第1圈有近1/2斜杆与球节点脱离,节点位移显著增大,但结构并未发生倒塌(图12(c));当PGA加至2300 gal时,模型底部第1圈的杆件几乎全部与球节点发生断裂,同时第2圈也有部分杆件与球节点脱开,结构因失去了底部杆件支撑而无法继续承载,最终整个结构向下坍塌(图12(d))。
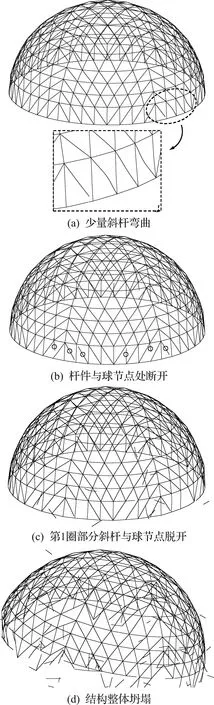
图12 试验模型的破坏过程数值仿真结果
6 结 论
在弹性DEM方法基础上,将粘结分布弹簧用梁纤维进行等效,推导了可考虑截面塑性开展的DEM纤维梁模型,实现了杆系结构弹塑性分析;在此基础上,提出了杆件断裂模拟算法,并编制了计算程序;将这一模型用于悬臂梁算例,模拟了悬臂梁从弹性小变形到弹塑性阶段,再到断裂和破坏的全过程,结果较为合理;最后将该方法应用于单层网壳倒塌破环行为模拟,分析结果表明数值仿真得到的网壳杆件断裂过程及结构倒塌模式与网壳振动台倒塌试验现象吻合,进一步验证了该方法的正确性。结论如下。
(1) 采用DEM纤维梁模型模拟杆件的断裂过程非常直观,只需定义弹簧的破坏准则即可实现球元之间的粘结消失与否;较FEM方法而言,不存在网格畸变和网格重划分及迭代不收敛等问题,更具计算优势。
(2) 本文方法虽可以描述杆件截面的渐进开裂过程,但只能描述结构的宏观破坏模式,还无法模拟材料内部裂纹的产生、开裂及扩展。后续还需进一步将DEM方法拓展用于精细化建模及仿真模拟,研究结构的细观或微观破坏模式,从而可以更深入地揭示结构的倒塌破坏机理。

