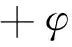矩形基础地基临塑荷载公式

许年春， 郑 瑞， 吴同情,2， 杨全虎

(1.重庆科技学院 建筑工程学院，重庆 401331；2.能源工程力学与防灾减灾重庆市重点实验室，重庆 401331)

1 引 言

临塑荷载是指地基中即将出现塑性区时的基底压力，对应基础荷载-沉降曲线(p-s曲线)上的比例界限，目前土力学教材中给出的临塑荷载公式是根据条形荷载作用下地基中应力分布推导出来的，因此只适用于条形基础[1-4]。文献[2,3]认为将条形基础地基临塑荷载公式应用于矩形基础，其结果偏于安全，但均没有推导理论公式，也没有提供实验数据。

对于条形基础临塑荷载的研究主要集中于两个方面,一是研究侧向土压力系数K0≠1时的临塑荷载[5,8]，但文献[5,8]在推导方法或利用开平方近似计算式方面存在争议，所给临塑荷载公式正确性值得商榷；二是研究考虑中间主应力影响的临塑荷载，如文献[9-12]采用双剪强度准则替换库仑强度准则，将中主应力引入临塑荷载公式，计算出的临塑荷载大于教材上的公式结果。

经查阅文献，未发现矩形基础地基临塑荷载公式的研究报道，而在实际工程中柱下矩形基础比条形基础应用更广泛，对矩形基础地基临塑荷载公式开展研究不仅对土力学学科发展具有理论意义，同时对矩形基础设计具有实践价值。

2 条形基础地基临塑荷载公式

条形基础的受力可看成平面应变问题，如图1所示，p表示基底压力，q表示基础埋深范围内土体自重产生的压力。

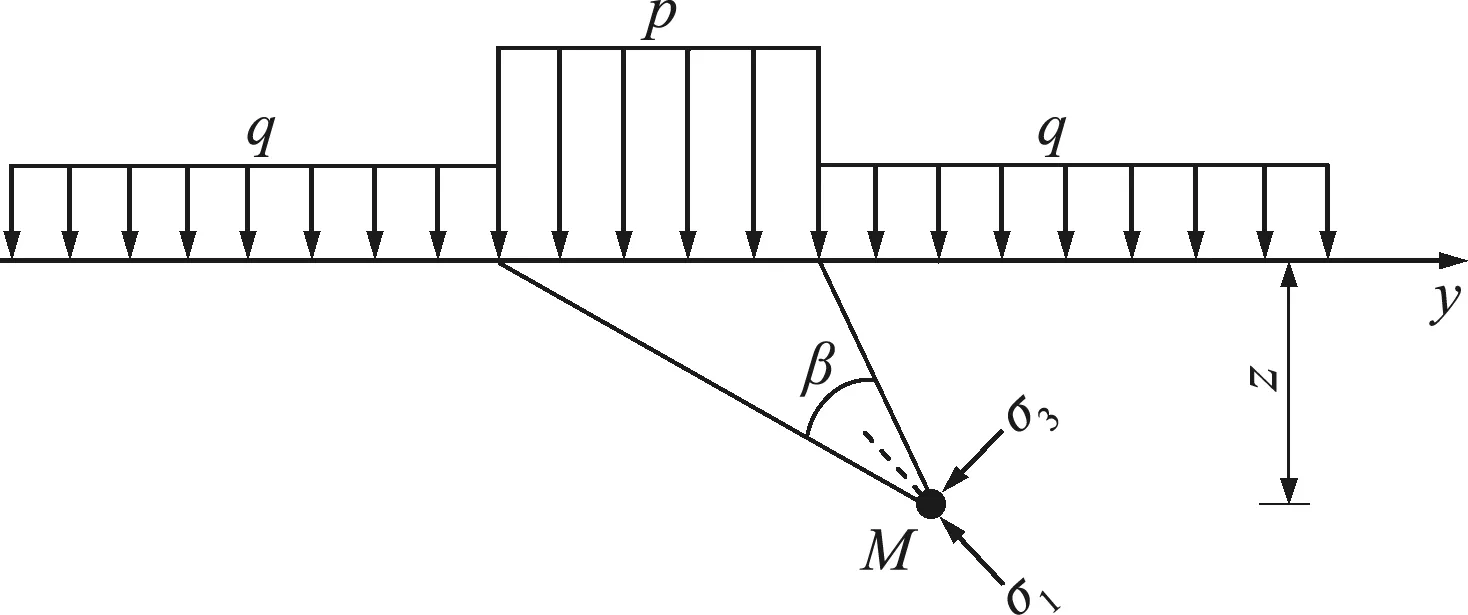
图1 条形基础地基中的附加主应力

under a strip footing

点M距基底的深度为z，β为点M到基底两端点的夹角。利用Flamant解可得到基底附加应力p-q在点M产生的主应力[1-4]为

(1a,1b)

且σ1作用在β的角平分线上。

基底面以下土体重度γ，当土体侧压力系数K0=1时，q和基底面以下土体自重压力γz在各个方向上产生相等的压力，相当于静水压力，因此原主应力方向不发生改变，主应力可通过直接相加得到，即[1-4]

(2a)

(2b)

(3)

实际地基土K0<1，临塑荷载小于式(3)的计算值，按照双剪统一强度理论，Coulomb强度准则计算出的临塑荷载偏小，如果把这两个因素一起考虑，按式(3)计算条形基础临塑荷载仍然是合理的。K0<1时土体自重应力会引起主应力轴的偏转，大大增加临塑荷载公式推导的难度；对于埋深较浅或地基承载力较大的基础，K0<1对于临塑荷载影响很小；双剪统一强度准则的中间主应力影响系数需要通过专门实验才能确定，综合考虑以上因素，本文推导矩形基础地基临塑荷载公式时，假设K0=1，采用Coulomb强度准则。

3 矩形基础地基临塑荷载公式

3.1 基底边缘处的应力分析

如图2所示为线框表矩形基础底面，其宽度为2a，长度为2b，基底附加压力为p-q，与条形基础相比，相当于在矩形基底左右两侧区域内作用向上的拉应力-p+q。

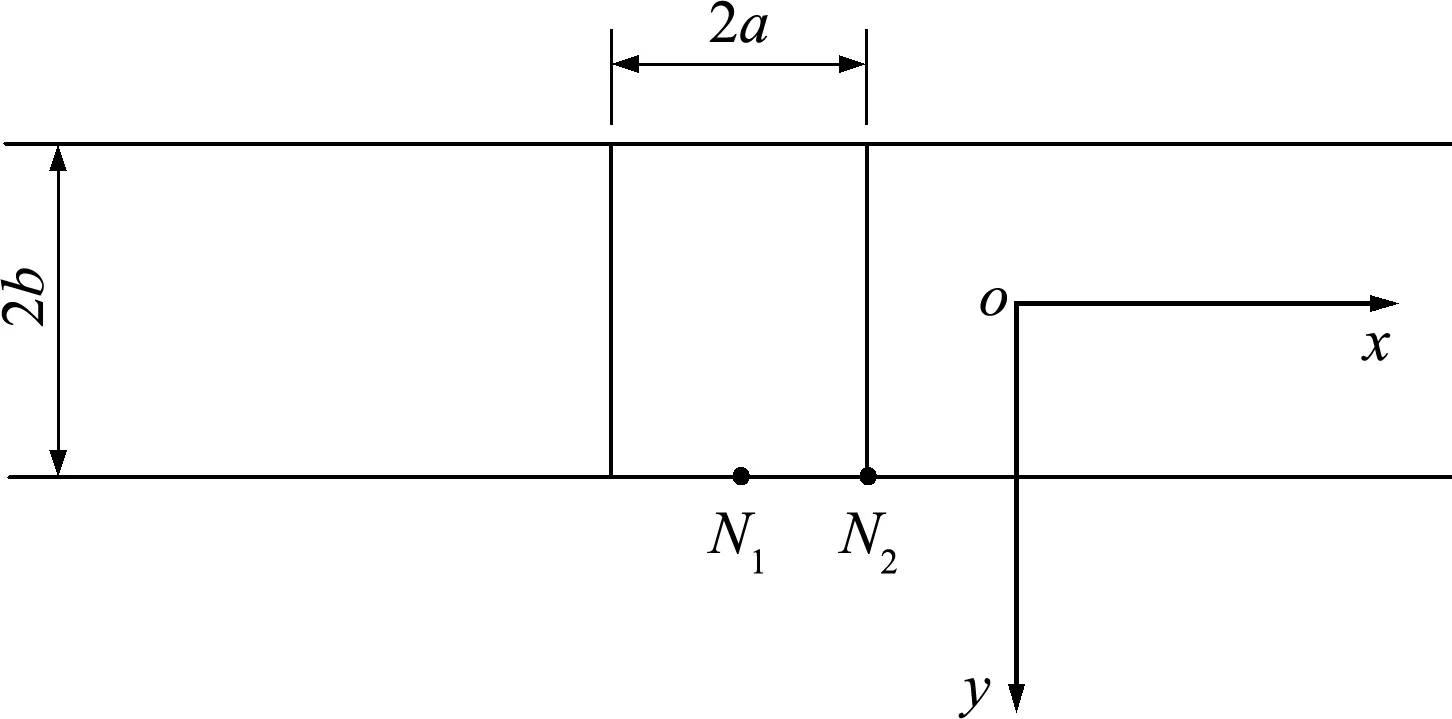
图2 矩形基础底面

将坐标原点O置于两侧区域内任一位置，如图2所示，x轴与宽度方向平行，y轴与长度方向平行，由于塑性区是从基底边缘处开始发展的，临塑荷载对应的塑性区开展深度为0，故取基底宽度方向边缘处中点N1和端点N2作为观察点。由于点N1的埋深z=0，根据Boussinesq单个竖向集中力作用下的应力解[2-4]，左右两侧区域内拉应力-p+q在点N1产生的y方向正应力为

(4)

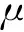
(5a)

对于条形基础，a≫b，atan[a/(2b)]≈π/2，σy 1 - p + q=0。

同时-p+q在点N1产生的z方向(竖向)正应力和剪应力分别为

σz 1 - p + q=0,τy z 1 - p + q=0

(5b,5c)

对于点N2，-p+q产生的y方向正应力为

(6)

式(6)积分可得

(7a)

同时-p+q在点N2产生的z方向正应力和剪应力分别为

σz 2 - p + q=0,τy z 2 - p + q=0

(7b,7c)

比较式(5～7)可知，-p+q在两点产生的竖向正应力和剪应力相等，y方向正应力差别在于最后一项，点N1为π/2-atan[a/(2b)]，点N2为π/2-(1/2)atan(a/b)，在后面的公式推导过程中，为了节省篇幅，只对点N1作详细介绍。

条形基底附加应力p-q和土体自重压力作用下,地基中主应力仍如式(2)，对于点N1和点N2，γz=0，大小主应力分别为

σ1=[(p-q)/π](β+sinβ)+q

(8a)

σ3=[(p-q)/π](β-sinβ)+q

(8b)

3.2 基底边缘处的应力表达式

沿条形基底地基中主应力方向建立y′-z′局部直角坐标系，如图3所示。

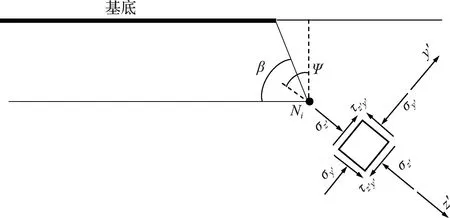
图3 局部直角坐标系

z′与竖向的夹角为Ψ，当点N1无限接近地面时，点N1与基底远端点连线近似为水平线，此时Ψ≈π/2-β/2，式(5)表示的应力在局部坐标系的应力为

(9a)

(9b)

(9c)

点N1的应力叠加为

(10a)

(10b)

τz′y′=τz′y′1 - p + q

(10c)

3.3 开平方近似计算式及误差分析

为得到地基临塑荷载公式，需要先根据式(10)中各应力分量求出大小主应力，再将主应力代入Coulomb抗剪强度公式。然而求大小主应力涉及到开平方求根，导致临塑荷载公式推导很困难，因此，需要利用开平方近似计算式。

(11)

式中n为正实数。

在Mohr应力圆中，点N1的应力可用点P和点Q的坐标来表示，如图4所示为P(σz′,τz′y′)和Q(σy′,-τz′y′)(注：β值预估范围1.0～1.8，由式(10)可以判断σz′>σy′，τz′y′>0)。PQ相对于σ轴的转角为2α。

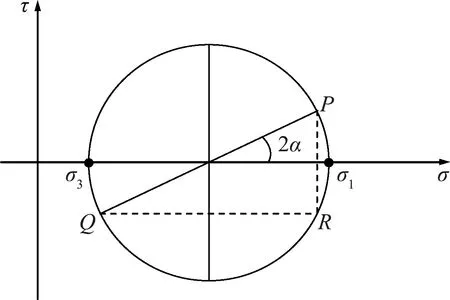
图4 用Mohr圆上的点表示应力分量

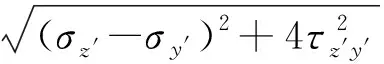
近似计算式的误差率用Δ来表示

(12)

对Mohr圆直径|PQ|任意取值，通过几何关系可得到不同2α值时的Δ值为

Δ=|100cos2α+100nsin2α-100|%

(13)

取n=0.06，0.08，0.1，0.12，0.14和0.16，分别作计算，图5给出2α∈(0,25°)时Δ值变化。

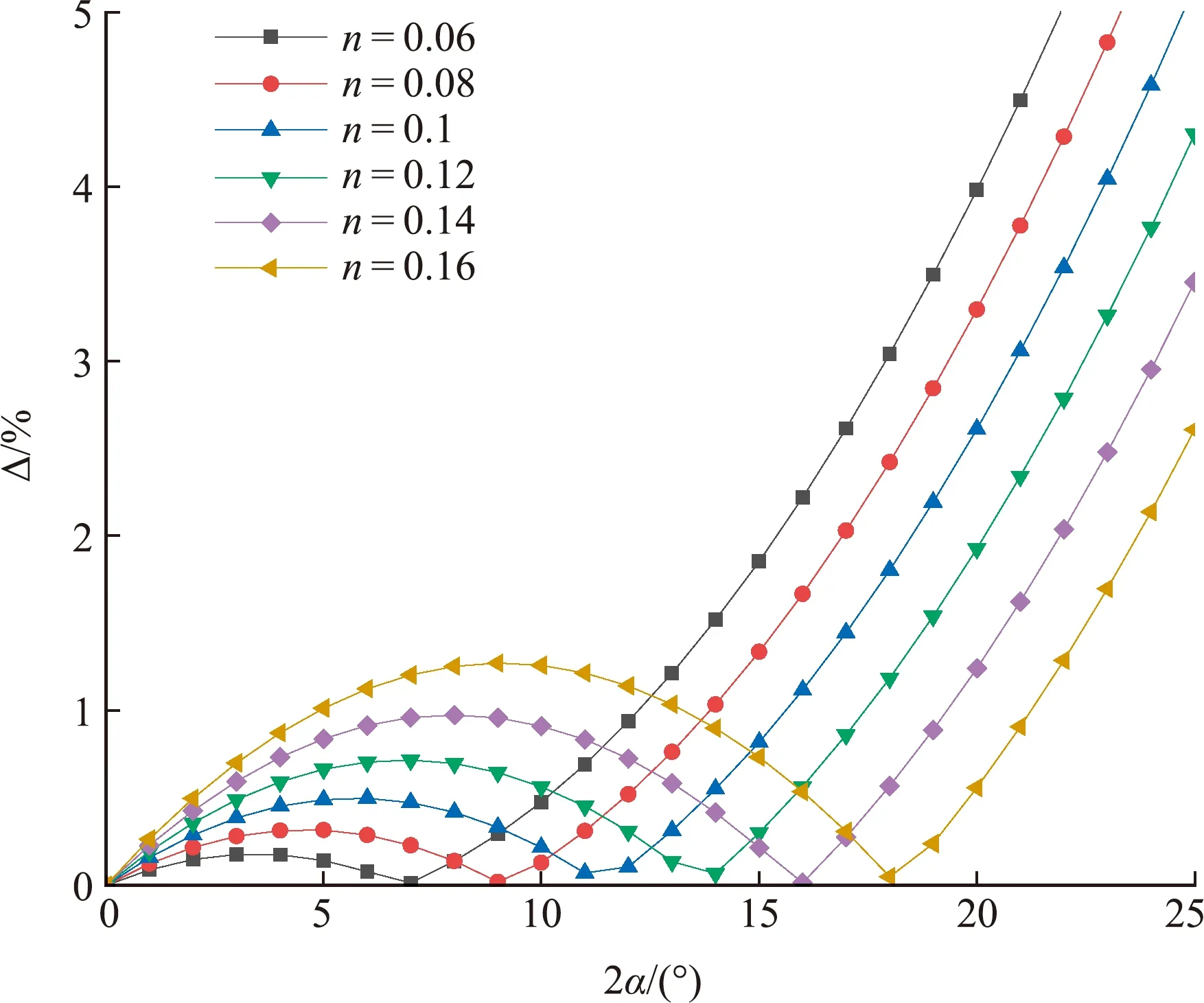
图5 2α -Δ关系

可以看出，随着2α的增大，Δ先增大，后变小，再逐步增大。当2α较小时，n取较小值时Δ较小，如2α=10°时，取n=0.08，Δ<0.13%。当2α较大时，n取较大值时Δ较小，如2α=19°时，取n=0.1，Δ=2.19%；取n=0.12，Δ=1.54%；取n=0.14，Δ=0.89%；取n=0.16，Δ=0.24%。

3.4 临塑荷载公式

土的Coulomb抗剪强度极限平衡条件为

(14)

根据主应力与应力分量的关系，极限平衡条件可以改写为

(15)

将式(10)各应力分量代入式(15)，利用开平方近似计算式(11)，经化简得到式(16)。

(16)

根据式(16)得p的表达式为

(17)

点N1临塑荷载pc r 1为p的最小值，式(17)右侧对β的导数等于0，得式(18)。

(sinβ+ncosβ)=0

(18)

利用三角函数的级数展开式,sinβ≈β-β3/6，cosβ≈1-β2/2+β4/27(注：取β∈(1.0,1.8)检验，最后一项分母取27，比取24有更高的精度)。

式(18)可转变为

Aβ4+Bβ3+Cβ2+Dβ+E=0

(19)

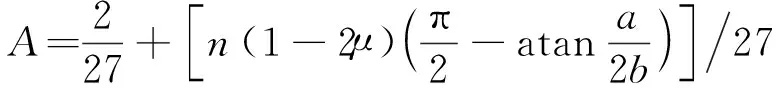
当n在0.06～0.16区间取值时，A的第二项相对于第一项很小，可以忽略(后面取多组参数进行检验，结果表明忽略该项引起的临塑荷载计算误差小于0.7‰)，将式(19)转换成式(20)。

β4+B′β3+C′β2+D′β+E′=0

(20)

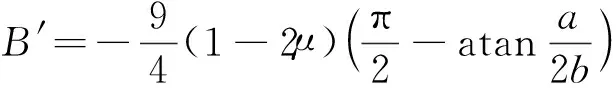
式(20)有四个实数解，数学手册上有其求解方法，限于篇幅，在此不作详细介绍，直接给出在(1.0,1.8)范围内的解为

(21)

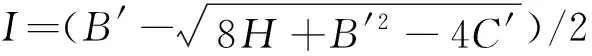
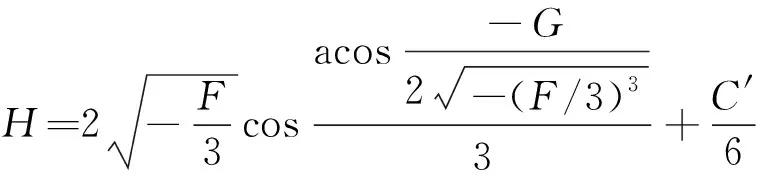
将式(21)代入式(17)，即可求出点N1临塑荷载pc r 1。

将式(17,21)的π/2-atan[a/(2b)]用π/2- (1/2)atan(a/b)来代替，即可得到点N2临塑荷载pc r 2。

4 算 例

表1列出了pc r 1/pc r s和pc r 2/pc r s的计算结果，其中n取值与计算出的2α值相关，2α=atan[2τz ′ y ′/(σz ′-σy ′)]，先取n=0.10，再根据计算出的2α值对n作调整(小幅调整n对2α没有影响，因此调整一次即可)，点N1与点N2的2α很接近(最大相差0.2)，点N2的2α略大，表1列出了点N2的2α及对应的Δ值。点N1与点N2的β几乎相等(最大相差0.01)，表1列出了点N2的β值。

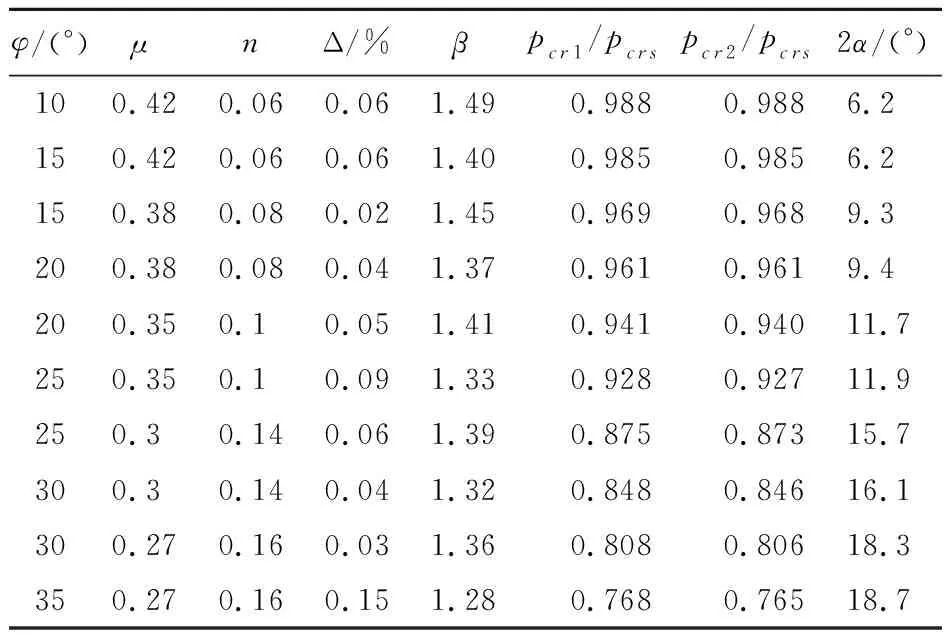
表1 pc r 1和pc r 2计算实例(a/b =0.5,c =20 kPa,q =30 kPa)

5 结 论