侧向受拉脆性岩石压缩本构及蠕变失效研究

李晓照， 车 行， 邵珠山， 戚承志

(1.北京建筑大学 土木与交通工程学院，北京 100044；2.西安建筑科技大学 理学院，西安 710055)

1 引 言

脆性岩石是深部地下工程围岩重要组成部分，此外，脆性岩石内部存在大量初始细观裂纹，外部荷载作用严重影响了脆性岩石内部裂纹扩展行为，进而影响岩石的宏观力学特性。众多学者通过试验研究了单轴压缩、三轴压缩、单轴拉伸及轴向拉伸侧向压缩作用下[1-4]，脆性岩石应力-应变关系，讨论了侧向压缩应力对岩石强度影响，并通过声发射、电镜扫描及CT扫描等技术分析了岩石内部细观裂纹变化情况。也有学者通过有限元、离散元和有限差分法等数值方法[5-7]，研究了不同外部荷载作用下的岩石力学特性及内部细观裂纹扩展行为。通过理论解析方法，研究了单轴压缩或三轴压缩作用下岩石内部细观裂纹扩展诱发的变形行为[8,9]。

以上是关于短时间内，侧向压缩荷载恒定，轴向压缩或拉伸荷载渐进增大作用下，脆性岩石准静态应力-应变本构关系的研究。当外部荷载长时间恒定不变时，脆性岩石蠕变特性研究对于评价深部地下工程围岩长期稳定性也有着重要的意义。因此，众多学者试验研究了单轴压缩、三轴压缩和单轴拉伸作用下脆性岩石的蠕变行为[10-12]，并结合弹性、粘性及塑性流变模块的不同组合，建立岩石蠕变模型；同时也通过声发射监测技术，研究了脆性岩石内部微裂纹变化行为。也有学者通过有限元和离散元等数值模拟方法[13,14]，研究了单轴压缩或三轴压缩作用下，脆性岩石内部细观裂纹诱发的蠕变力学特性。此外，通过理论解析方法，还研究了单轴压缩或三轴压缩作用下，脆性岩石内部细观裂纹扩展演化诱发的宏观变形力学行为[15]。

综上，关于侧向拉伸与轴向压缩荷载作用下，脆性岩石内部细观裂纹变化力学机理及该机理与宏观变形关系尚不清楚。深部地下隧道开挖卸载过程中，隧道围岩承受的应力状态可能会发生各种变化，其中侧向拉伸且轴向压缩也是一种重要的受力状态[16,17]，精确地判断该应力状态下的力学特性，对深部隧道围岩稳定性评价也具有重要意义。

因此，本文将在前期关于侧向及轴向均为压缩应力作用下岩石力学模型的[8,15]基础上，进一步研究侧向拉应力对轴向压缩应力作用下脆性岩石的应力-裂纹扩展关系、应力-应变本构关系，以及岩石蠕变裂纹长度及应变演化特性的影响。

2 理论模型

2.1 裂纹扩展导致的轴向压缩应力-应变本构关系

基于图1中轴向压缩应力作用下细观翼型裂纹力学模型，裂纹尖端应力强度因子为[8,15,18]

(1)

(2)

(3)

S=π1/3[3/(4NV)]2/3

(4)

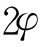
(5)

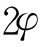
(6)

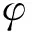
图1 侧向受拉且轴向压缩脆性岩石细观裂纹扩展模型

裂纹应力强度因子KI达到临界值KI C时，岩石发生断裂。因此，基于式(1)，岩石的应力状态与扩展裂纹长度间的关系为[8]

(7)

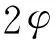
(8)

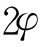
(9)

B3=[π(l+βa)]-3/2+

(10)

基于细观与宏观定义的损伤，宏观应变与细观裂纹扩展间的关系可建立为[19]

ε1=εo[-ln(1-(l/a+1)3Do)]1/m

(11)

式中m和εo为材料常数。将l=0代入方程(11)，得到裂纹启裂应变ε1c i；将llim代入方程(11)，得到岩石裂纹贯通极限应变ε1f，该值可近似判断岩石失效应变。

将式(11)代入式(7)，翼型裂纹扩展诱发的轴向应力与应变本构关系[19]为

(ε1c i<ε1<ε1f)(12)

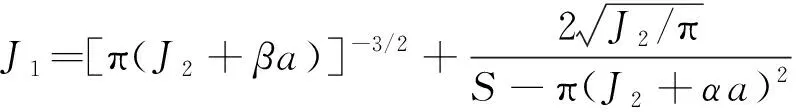
(13)

(14)

此外，翼型裂纹启裂前(即l=0)的应力应变关系假设为线性弹性行为。将l=0代入方程(7)，可得到裂纹启裂应力σ1c i，结合裂纹启裂应变ε1c i，经计算，裂纹启裂前应力-应变关系可以表示为

(0<ε1≤ε1c i)(15)

式(12，15)共同描述了岩石初始弹性、应变硬化与软化及失效阶段的应力-应变关系。

2.2 侧向拉压应力判别条件

本文理论模型中压缩应力为负值，拉应力为正值。模型中岩石裂纹扩展机制可以描述为，远端应力作用下，岩石内部初始裂纹面的剪切应力克服初始裂纹面法向压应力导致的摩擦力，进而引起初始裂纹两端产生翼型裂纹扩展。因此，本文模型需满足不等式关系(16)，

(16)

通过求解不等式(16)，得到轴向压应力作用下，侧向应力为拉压应力时需要满足的参数范围为

(17)

(18)

满足不等式(17)，侧向应力为压缩应力时，脆性岩石力学关系已经得到广泛研究[8,15,19]。然而，对于满足不等式(18)条件的脆性岩石拉应力作用下，岩石轴向压缩力学行为研究很少，因此，本文重点关注该方面的研究。

此外，值得注意的是，不等式(18)中，当侧向应力为拉应力时，岩石内部初始裂纹面上的法向应力是压缩应力，即σn<0。那么是否存在初始裂纹面法向应力为拉应力的情况。如果存在，则初始面摩擦力消失，则不等式关系满足

(19)

根据不等式(19)，求解得到轴向压缩应力作用下，初始裂纹面法向应力为拉应力时，需要满足的参数要求如下，

(20)

如果初始裂纹面法向应力为拉应力，则导致裂纹扩展的楔力Fw重新定义为

(21)

将方程(21)替换方程(2)，则一个新的类似于方程(7)的应力-裂纹扩展关系和方程(12)的应力-应变关系方程可以推出。然而，经过计算发现，在固定侧向拉应力作用，轴向压缩应力渐进变化而引起的翼型裂纹扩展过程中，不能同时满足方程(20)条件，即初始裂纹面法向应力为拉应力的情况不可能出现。因此，本文模型关于侧向受拉，轴向压缩应力作用下，脆性岩石内部初始裂纹面法向应力只能取负，即为压缩应力，考虑初始裂纹面摩擦系数。

2.3 侧向受拉且轴向压缩脆性岩石蠕变失效方程

对于脆性岩石侧向受拉、轴向压应力作用下，裂纹扩展诱发的蠕变时间演化力学特性，可结合应力强度因子方程(1)与亚临界裂纹扩展法则dl/dt=v(KI/KI C)n [20]，满足不等式(18)的条件下，翼型裂纹扩展速率演化方程为

(22)

式中v为特征裂纹速率，n为应力腐蚀参数。求解微分方程(22)，可推出翼型裂纹长度时间演化结果。给定应力状态下微分方程的初始裂纹长度可通过方程(7)应力-裂纹长度关系获得。方程(22)侧向应力定义为与时间相关函数σ3(t)，可分析侧向应力变化路径影响下的岩石蠕变裂纹扩展行为。

早晨刮胡子，剃须刀断了。我也没怎么用力，可是剃须刀的脖子却啪的一声，断了。一次性剃须刀？当然不是。这是吉列公司的最新产品，价格将近六千元。再没有比它更结实的了，如果不是有人故意把它弄断，它不可能自己折断。我才用了一个月，就变成了这样。

结合方程(22)得到的翼型裂纹长度演化结果与方程(11)，裂纹扩展导致的轴向应变演化为

(23)

3 结果与讨论

本文基于前期提出的锦屏大理岩三轴压缩应力应变本构关系及蠕变演化宏细观力学模型[8,15]，考虑初始裂纹面法向应力及剪切应力正负方向判别条件，展开进一步深入研究。具体模型参数选取方法参考文献[8]。由于目前轴向渐进压缩、侧向拉伸作用下的实验研究较难实施，因此本文是在前期已经验证的三轴压缩宏细观理论模型基础上的预测与讨论。具体研究结果如下。

3.1 侧向拉压应力对初始裂纹面楔力影响

初始裂纹面上的楔力，对于侧向受拉压作用，轴向压缩岩石力学行为有着重要的影响。图3给出了侧向拉压应力对楔力的影响曲线，侧向应力由压到拉转化过程中，楔力不断增大，即侧向压应力越大，楔力越小，侧向拉应力越大，楔力越大。

图2研究了初始裂纹尺寸、摩擦系数及裂纹角度对楔力与侧向应力关系的影响。随着初始裂纹尺寸增大和摩擦系数的减小，在给定侧向应力时，楔力越大。随着裂纹角度的增大，给定侧向应力，楔力先增大，后减小，即存在一个最不利裂纹角度。文献[8]对于裂纹角度对轴向与侧向压缩作用下的应力应变本构曲线进行了详细讨论，本文在此基础上进一步研究的轴向压缩与侧向拉伸作用下应力应变曲线存在相同的变化趋势，因此不再赘述，本文将重点分析侧向拉应力对岩石轴向压缩应力应变曲线及压缩蠕变演化曲线的影响。

图2 侧向应力与楔力关系

3.2 侧向拉压应力对轴向渐进压缩失效特性影响

图3给出了侧向应力由压应力到拉应力转换过程中，岩石压缩轴向应力与裂纹长度关系曲线、轴向应力与轴向应变关系曲线、初始弹性模量、裂纹启裂应力及峰值强度变化规律。

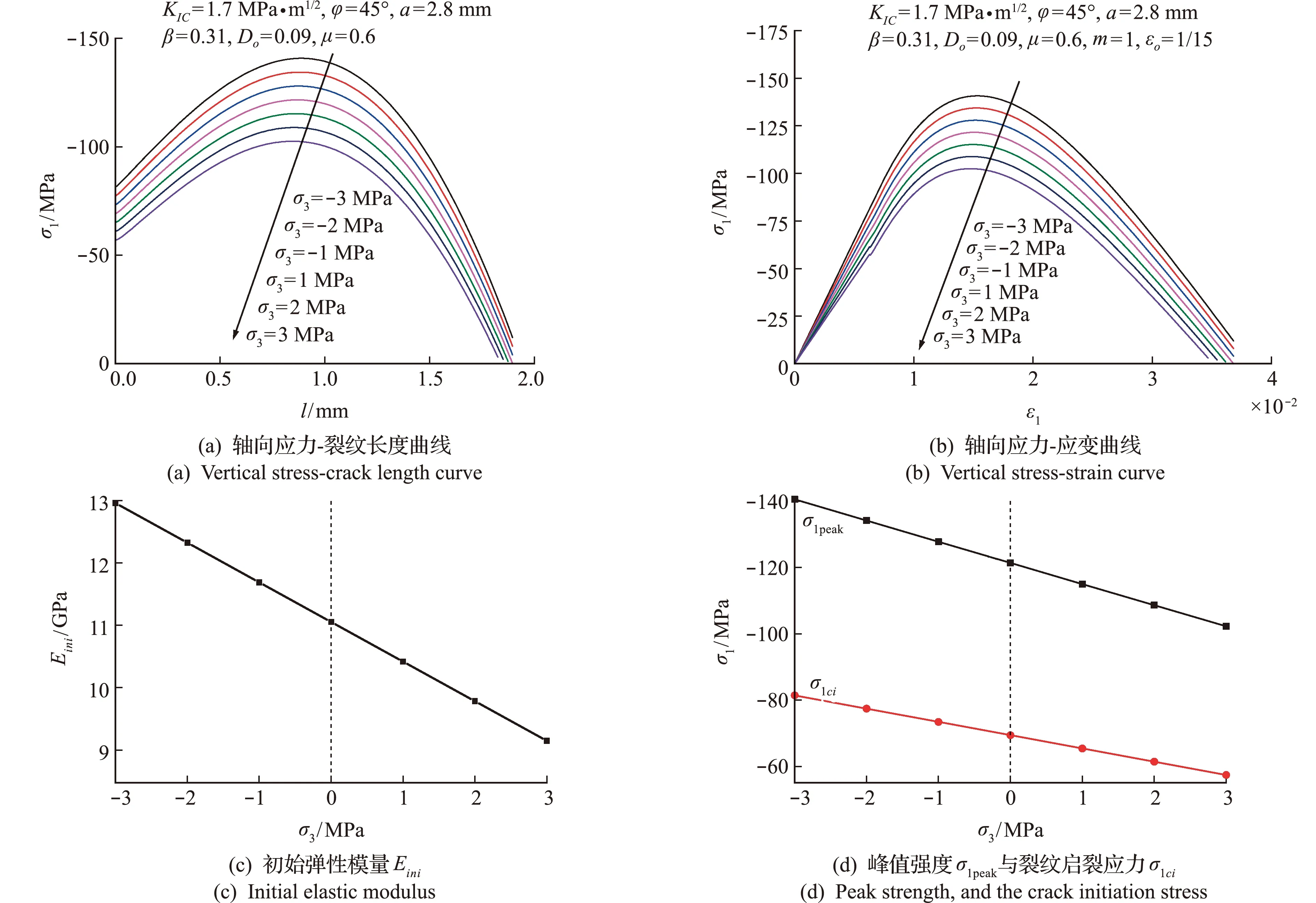
图3 侧向拉压应力对轴向应力-裂纹长度曲线、轴向应力-应变曲线、初始弹性模量Ei n i、峰值强度σ1peak与裂纹启裂应力σ1 c i的影响

在轴向应力与裂纹长度关系曲线、轴向应力与轴向应变关系曲线中，在给定裂纹长度或应变下，随着侧向压应力增大，轴向应力不断增大；随着侧向拉应力增大，轴向应力不断减小。随着侧向压缩应力增大，岩石初始弹性模量、裂纹启裂应力及峰值强度逐渐增大，随着侧向拉应力增大，岩石初始弹性模量、裂纹启裂应力及峰值强度逐渐减小。图3(d)中侧向拉应力下的裂纹启裂应力与峰值强度之间的轴向应力取值范围，为侧向拉伸与轴向压缩蠕变特性的恒定应力状态选取提供了依据。

3.3 侧向拉应力对轴向压缩蠕变失效特性影响

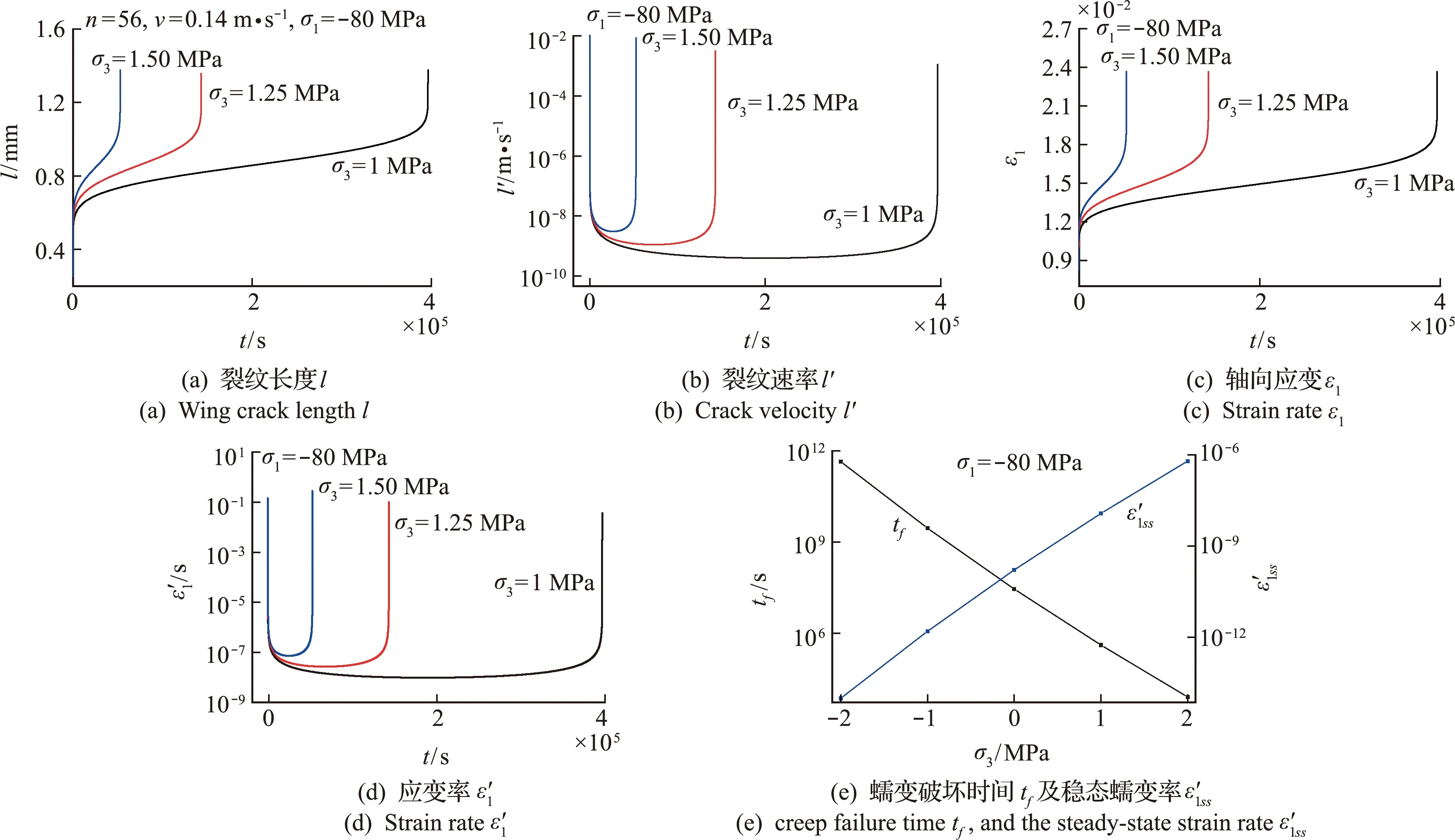
图4 侧向拉应力对蠕变过程中裂纹长度l、裂纹速率l′、轴向应变ε1、应变率蠕变破坏时间tf及稳态蠕变率影响

3.4 侧向拉-压应力突变对轴向压缩蠕变失效影响

3.3节研究了恒定轴向压缩应力与恒定侧向拉压应力作用下的脆性岩石蠕变演化曲线。图5(a,b)研究了侧向应力由压应力到拉应力的突变转化，对轴向压缩蠕变裂纹长度、裂纹速率、轴向应变及应变率演化曲线的影响。在侧向压应力阶段，裂纹长度及轴向应变经历了减速增大到稳态增大的蠕变演化，在侧向拉应力阶段，裂纹长度及轴向应变经历了减速增大、稳态增大及加速增大直至失效的蠕变演化。侧向应力由压到拉的突变，导致了裂纹速率或轴向应变率的突增，进而导致在短时间内裂纹长度或轴向应变也产生了一个较大的增量。

图5 侧向拉-压应力突变及压-拉应力突变对轴向压缩蠕变裂纹长度及应变演化影响

在侧向拉应力阶段的稳态裂纹速率及应变率均大于侧向压应力阶段的稳态裂纹速率及应变率。

图5(c,d)研究了侧向应力由拉应力到压应力突变转化，对轴向压缩蠕变裂纹长度、裂纹速率、轴向应变及应变率演化曲线的影响。在侧向拉应力阶段，裂纹长度及轴向应变经历了减速增大、稳态增大及加速增大的蠕变演化，此时的加速蠕变并没有导致岩石的最终失效；在侧向压应力阶段，裂纹长度及轴向应变经历了稳态增大及加速增大直至失效的蠕变演化。侧向应力由拉到压的突变，导致了裂纹速率或轴向应变率的突降，进而导致在较长时间内裂纹长度或轴向应变增量不大。侧向压应力阶段的稳态裂纹速率及应变率均小于侧向拉应力阶段的稳态裂纹速率及应变率。

3.5 侧向拉应力分级加载对轴向压缩蠕变失效影响

图6给出了侧向拉应力分级增大作用下，轴向压缩蠕变裂纹长度、裂纹速率、轴向应变及应变率演化曲线。随着侧向拉应力分级增大，裂纹长度及轴向应变都分别经历了多次的减速增大至稳态增大演化，直至最后一次侧向拉应力增大，在短时间内裂纹长度及轴向应变分别经历了一个减速增大、稳态增大及加速增大的演化，直至岩石最终失效。

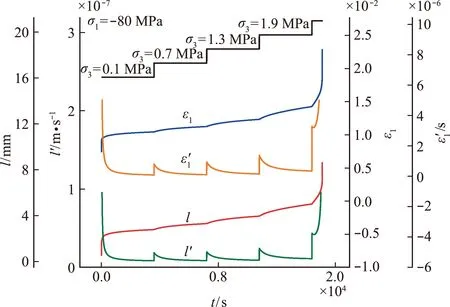
图6 侧向拉应力分级加载及轴向恒定压缩应力作用下，脆性岩石蠕变翼型裂纹长度、裂纹速率、轴向应变及应变率演化曲线

loading of lateral tensile stress and the constant axial stress

4 结 论

基于脆性岩石细观裂纹扩展模型中初始裂纹面法向应力与剪切应力正负方向关系，确定了轴向压缩作用下，侧向应力拉压判别条件。提出侧向受拉的轴向压缩应力-应变本构关系，以及轴向压缩蠕变应变演化模型。结论如下。

(1) 侧向恒定拉应力和轴向压缩应力渐进变化过程中，脆性岩石内部初始裂纹面法向应力为压应力。侧向应力由压缩转化为拉伸时，脆性岩石峰值强度、裂纹启裂应力与弹性模量均逐渐减小。即峰值强度、裂纹启裂应力及弹性模量随侧向压应力增大而增大，随侧向拉应力增大而降低。

(2) 在恒定轴向压缩蠕变作用下，由侧向压应力逐渐转化为拉应力的过程中，岩石蠕变失效时间不断减小，岩石稳态蠕变应变率不断增大。当侧向应力由压应力突变为拉应力，导致了裂纹速率或轴向应变率的突增，进而导致在短时间内裂纹长度或轴向应变产生较大的增量；侧向应力由拉到压的突变，导致了裂纹速率或轴向应变率的突降，进而导致在较长时间内裂纹长度或轴向应变增量不大。

(3) 随侧向拉应力的分级增大，裂纹长度及轴向应变都分别经历了多次的减速增大至稳态增大的演化，直至最后一个侧向拉应力阶段，岩石裂纹长度及轴向应变产生加速增大，直至岩石失效。

本文提出的脆性岩石宏细观力学模型中，所有裂纹尺寸或角度均假设为相同值，且仅考虑了两个裂纹间相互作用，是一种平均化方法。该方法不能很好地分析随机裂纹分布下，多个裂纹相互作用下导致的岩石非均力学特性。因此，如何研究随机分布裂纹岩石力学特性是需要进一步解决的问题。