谈谈多变元问题的思考策略——从2022年一道高考题的解法说起

宋秋林 何拓程特级教师

(1.江苏省姜堰第二中学 2.北京理工大学附属中学)

1 试题呈现

题目 (2022年新高考Ⅱ卷12,多选题)若x,y满足x2＋y2－xy＝1,则( ).

A.x＋y≤1 B.x＋y≥－2

C.x2＋y2≤2 D.x2＋y2≥1

分析 这是2022年新高考Ⅱ卷第12题,作为多选题,此题的本质是求x＋y和x2＋y2的取值范围.而已知条件中的x,y并非函数关系,由此求解问题就变得困难重重.本文以此题作为载体,谈谈求解多变元问题常用的思考策略.

2 解法探究

思路1 构造方程

方程作为已知量和未知量的矛盾统一体,可以充当由已知探索未知的桥梁.本题的两个变量地位相同,但是不易将一个变量用另一个变量表示.因此,变换思路,将关系式当作方程,使其中一个量作为主元,其他的当作参量,通过方程有解,即可求出参量的取值范围(也称主元法),利用这一思想,将目标量变换成参量进行求解.

解法1 设x＋y＝t,所以y＝t－x,将其代入x2＋y2－xy－1＝0,得3x2－3tx＋t2－1＝0,因为方程有解,所以Δ＝9t2－4×3(t2－1)≥0,解得－2≤t≤2,即－2≤x＋y≤2.

设x2＋y2＝λ,则

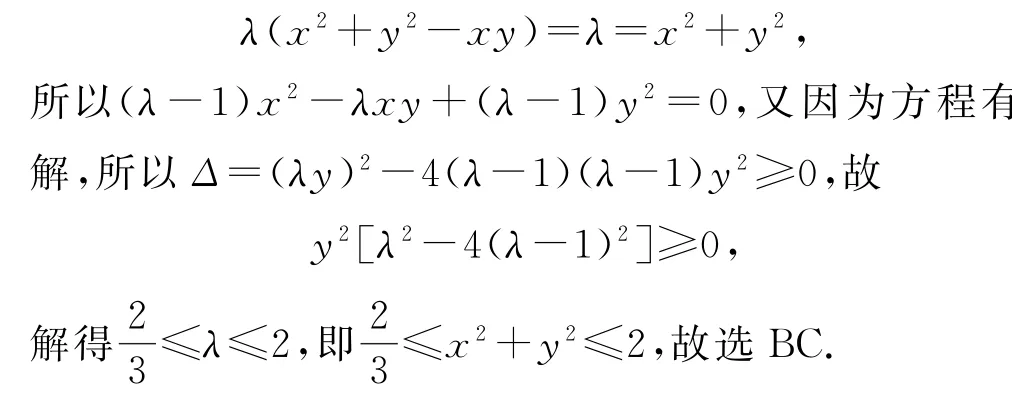
思路2 构造函数

函数思想是重要的数学思想,在中学阶段,函数思想更是贯穿整个教学的始终.本题的难点就是不能流畅地构造函数,注意到等式左边是二次齐次式,因此将目标量化为二次式,利用函数的性质求解.

思路3 构造不等式

综合考虑条件式与目标量的结构特征,运用均值不等式等方法进行整体处理,直接探求目标量取得最值的条件.事实上,均值不等式是解决多变元问题的主要方法.

可知图形是对称轴为x±y＝0的椭圆(如图1).

图1

3 真题链接

有意思的是,2019年高考数学北京卷理科第8题与本题有相似之处.

例1 (2019年北京卷8)数学中有许多形状优美、寓意美好的曲线,曲线C:x2＋y2＝1＋|x|y就是其中之一(如图2).给出下列三个结论:

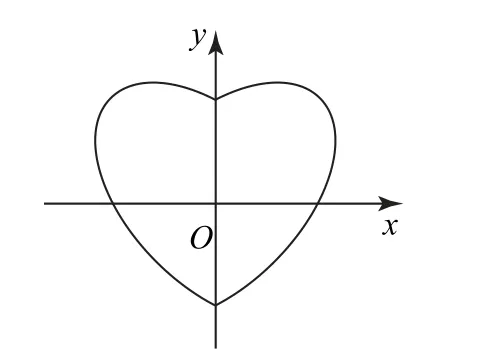
图2

①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);

②曲线C上任意一点到原点的距离都不超过2;

③曲线C所围成的“心形”区域的面积小于3.其中,所有正确结论的序号是( ).

A.① B.②

C.①② D.①②③

分析 如果了解“心形”曲线的变换过程(如图3),很快就会得到答案,本题选C.

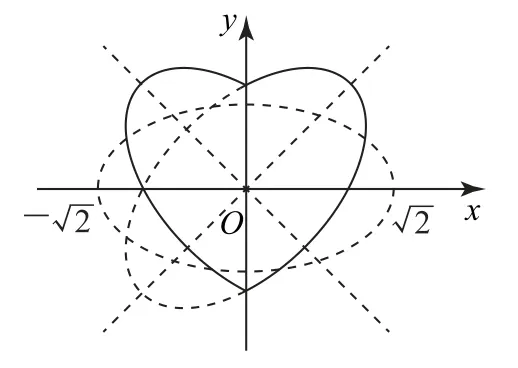
图3

4 问题拓展

5 解题反思

高考功能的定位是“立德树人、服务选才、引导教学”.因此,关注并研究高考题是每个教师必须做的功课.同时,在解题教学中,启发学生多角度、多层次地对同一个问题进行分析和研究,实际上就是在梳理数学知识内在的逻辑关系.因为,任何新知识的产生,都是在原有知识的基础上进行延伸和扩展的.事实上,理解就是能用已有的知识多角度、全方位地解释未知的东西,这种寻求数学思维逻辑性的过程就是思维品质提升的过程,同时也是学生核心素养发展的过程.另外,本题中极坐标、坐标旋转并不是高考要求考查的内容.但是,作为整个数学知识体系的一部分,对于学有余力的学生,进行一些拓宽,使其知识面更加全面和完整是非常有必要的.