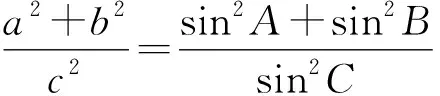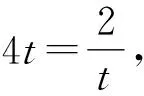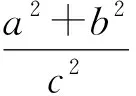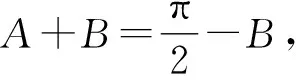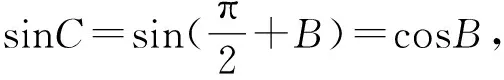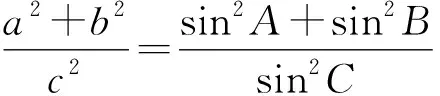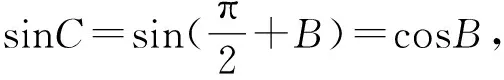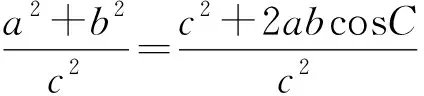探究2022年新高考Ⅰ卷第18题的多种解法及启示
李增涛
(江苏省扬州市仙城中学 225200)
1 试题再现
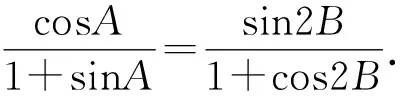
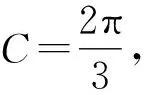
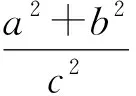
2 解法探析
2.1 第(1)问解析

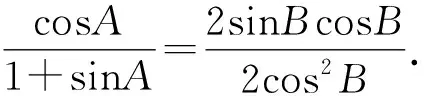
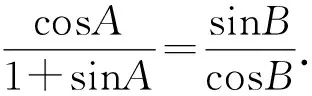
即cosAcosB=sinB+sinAsinB.
即cos(A+B)=sinB.
得cos(π-C)=sinB.
即-cosC=sinB.
即cosC=-sinB.(说明C为钝角,B为锐角)
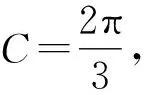


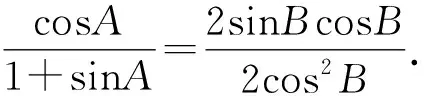
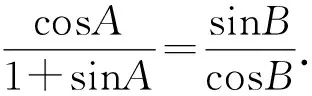
即cosAcosB=sinB+sinAsinB.
由cos(A+B)=sinB.(学生自然能联想到余弦函数在(0,π)上是单调函数和诱导公式)
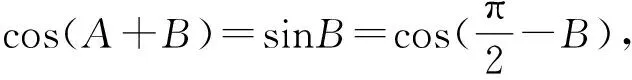
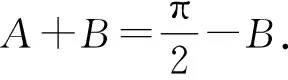
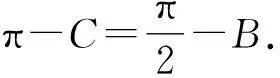
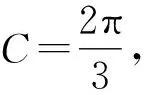

cosA(1+cos2B)=sin2B(1+sinA).
即cosA+cosAcos2B=sin2B+sin2BsinA.
即cosAcos2B-sin2BsinA=sin2B-cosA.
即cos(A+2B)=sin2B-cosA.
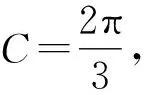
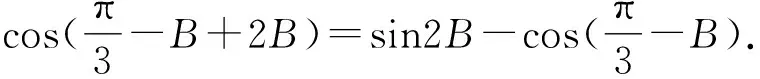
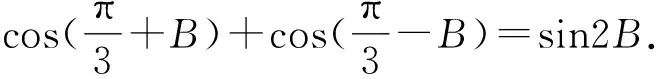
即cosB=2sinBcosB.
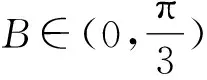
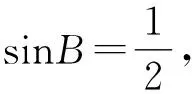

解法4 由题意可知

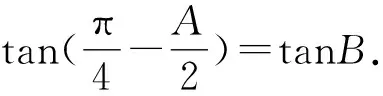
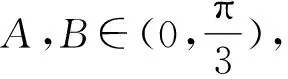
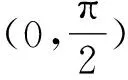
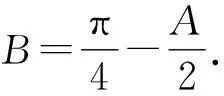
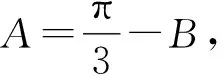

2.2 第(2)问解析
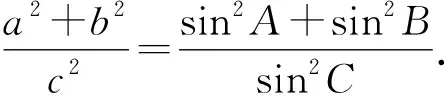
由(1)得-cosC=sinB.
即cosC=-sinB且C为钝角,B为锐角.
而这个式子还容易联想到平方关系,利用平方关系消元即
sin2A=sin2(B+C)
=(sinBcosC+cosBsinC)2
=(-cos2C+sin2C)2
=(2cos2C-1)2
=4cos4C-4cos2C+1,
令1-cos2C=t,则0 解法2 由(1)得cos(A+B)=sinB. (以下同解法2) 从本题的解法可以发现命题者的一个意图:大部分学生对于如下两种转化很熟悉: (1)互补转化:如cos(A+B)=-cosC; sin(A+B)=sinC. 但是本题要分析化简等式:-cosC=sinB,该式对中等靠刷题的学生而言就有困难了,不能随机应变导致学生在短时间内不能清晰地化简出来,找不到解题方向,所以我们在平时的教学中既要归纳总结常见结论,更要注重结论的得来过程,认清变化的本质,不能仅靠刷题来提升解决问题的能力. 实际上,对于我们教师而言,摆在我们眼前的问题就是怎样优化高中数学教学过程,怎样深度思考发现教学的本质,以此来促进学生的核心素养提升.