边角关系双管齐下黄金三角迎刃而解——谈一道解三角形质检问题的多解、背景与启示

唐 洵

(福建省福清第三中学 350000)

1 问题呈现

题目(2022年福州质检)记△ABC的内角A,B,C的对边分别为a,b,c，已知c=acosB+ccosA.

(1)试判断△ABC的形状，并说明理由；

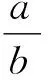
此题难度中等，试题以等腰三角形及多三角形问题的边角关系为背景，侧重考查正余弦定理的使用，以及数形结合思想在解三角形问题中的应用；与2022年新高考Ⅰ卷19题相比较，两个问题异曲同工，体现了命题者对新高考试卷的理解入木三分.

2 问题破解

2.1 第(1)问解析

对于第(1)问，利用题设条件中的边角混合关系式求解，难度不大，其解题思路一般有三种，一是利用正弦定理实现边化角后，转化为三角函数公式的应用；二是利用余弦定理实现角化边后，转化为对代数式的化简；三是利用课本推论中的射影定理对单独存在的边进行替换后，对代数式进行化简.此法较为简单.基于上述思路，便有如下解法.

解法1由正弦定理，得

sinC=sinAcosB+sinCcosA.

因为sinC=sinπ-(A+B)

=sin(A+B)

=sinAcosB+cosAsinB，

故sinAcosB+cosAsinB=sinAcosB+sinCcosA.

即cosAsinB-sinCcosA=0.

即cosA(sinB-sinC)=0.

故cosA=0或sinB=sinC.

则A=90°或b=c.

故△ABC为直角三角形或等腰三角形.

解法2 由余弦定理，得

两边同乘2bc，得

2bc2=a2b+c2b-b3+b2c+c3-a2c.

故a2b-c2b-b3+b2c+c3-a2c=0.

则(a2b-a2c)+(b2c-b3)+(c3-c2b)=0.

即a2(b-c)+b2(c-b)+c2(c-b)=0.

故(c-b)(b2+c2-a2)=0.

故b2+c2=a2或b=c.

故△ABC为直角三角形或等腰三角形.

解法3由射影定理，得

c=acosB+bcosA.

故acosB+bcosA=acosB+ccosA.

即bcosA=ccosA.

则(b-c)·cosA=0.

故cosA=0或b=c.

则A=90°或b=c.

故△ABC为直角三角形或等腰三角形.

2.2 第(2)问解析

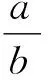
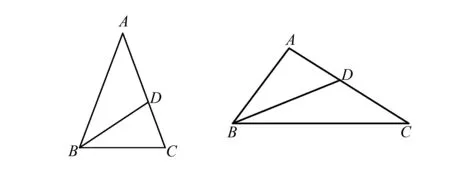
图1 图2

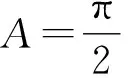
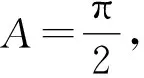
因为sin∠ADB=sin∠ABC，

而sin∠ABC=sin∠ACB，

故sin∠ADB=sin∠ACB.

而∠ADB≠∠ACB，

故∠ADB+∠ACB=π.

又∠ADB+∠BDC=π，

故∠BDC=∠ACB.

故AD=BD=BC=a,CD=AC-AD=b-a.

以下有两种解题方法：

方法1在△ABD中，

在△BCD中，

而cos∠ADB+cos∠CDB=0，

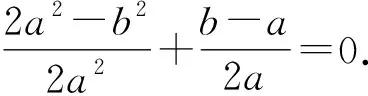
即a2+ab-b2=0.

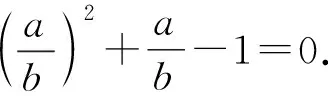
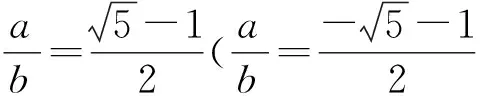
方法2在△BCD中，

在△ABC中，

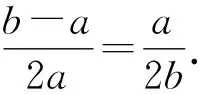
即a2+ab-b2=0.

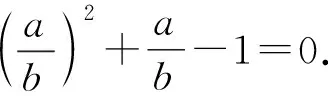
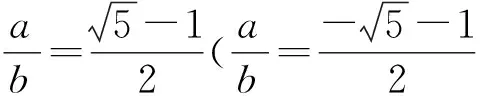
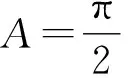
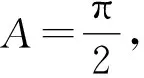
因为sin∠ADB=sin∠ABC，

而sin∠ABC=sin∠ACB，

故sin∠ADB=sin∠ACB.

而∠ADB≠∠ACB，故∠ADB+∠ACB=π.

而∠ADB+∠BDC=π，故∠BDC=∠ACB=α.

则∠ADB=π-α.

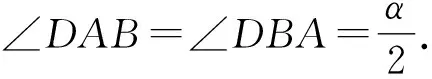
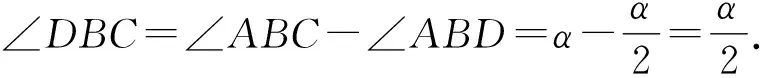
以下有五种解题方法：

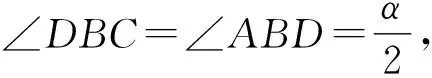
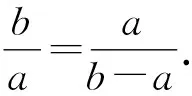
即a2+ab-b2=0.

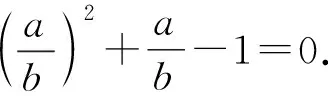
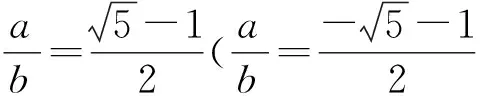
方法2在△BDC中，由正弦定理，得

在△ABC中，由正弦定理，得

两式相乘可得，AC·DC=BC2.

即b·(b-a)=a2.

即a2+ab-b2=0.

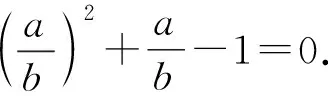
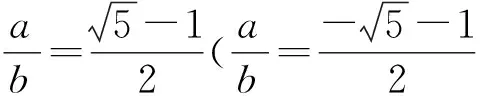
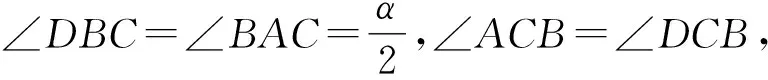
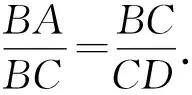
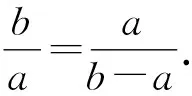
即a2+ab-b2=0.

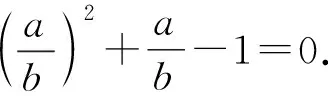
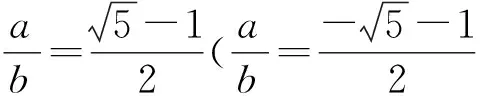
方法4因为S△ABC=S△ABD+S△BCD，

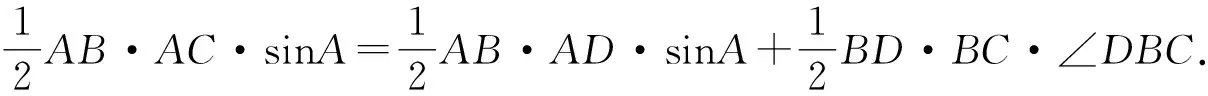
即AB×AC=AB×AD+BD×BC.

故b2=ab+a2.

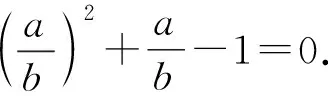
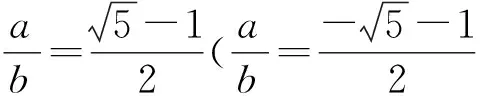
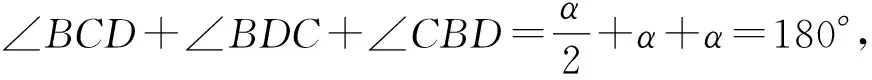
解得α=72°.

在△ABC中，由正弦定理，得

下面求cos36°的值；

因为sin36°=cos54°=cos(36°+18°)，

故2sin18°cos18°=cos36°cos18°-sin36°sin18°.

故2sin18°cos18°=(1-2sin218°)cos18°-2sin218°cos18°.

则2sin18°=1-2sin218°-2sin218°.

故4sin218+2sin18°-1=0.

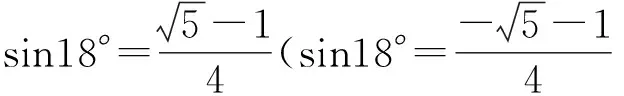
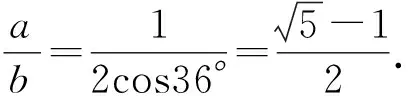
3 追本溯源

本题第(1)问的命题背景为射影定理，定理表述为：记△ABC的内角A,B,C的对边分别为a,b,c，则a=bcosC+ccosB①，b=acosC+ccosA②，c=acosB+ccosB③；命题者将等式③中等号右侧的ccosB更换为ccosA，于是得到问题(1)，侧重考查学生逻辑推理以及数学运算的核心素养，体现了化归与转化的数学思想.

4 学习启示

(1)解三角形问题的实质是研究三角形中的边角关系，因此在解题时，可以教学生从边或角的方向入手，在对应的三角形中利用正弦定理或余弦定理进行解题，有时也利用面积公式作为边角转化的桥梁.

(2)对于边角混合的题设条件，往往是纯代数问题，利用正弦定理或余弦定理都能求解，其不同点在于，利用正弦定理多是化角，进而与两角和差的正余弦公式、辅助角公式、诱导公式等配合使用解题；利用余弦定理多是化边，进而合理配对，实现等式的化简；教师平时教学的过程中务必强调此类问题的一题多解，并且亲身演示，让学生形成解题的反射弧，提高此类问题的得分率.

(3)图形背景下的解三角形问题，常以多三角形问题或四边形问题为命题背景，此时要关注题设中的已知量，看看是否为两角一边、两边一夹角、两边一对角以及三边的问题，进而选择合适的解题策略；尤其关注公共边以及公共角，以此为据，列式解题.

(4)解三角形问题没有复杂的二级结论，在教学的过程中，应及时总结课本练习以及高考试题中出现过的二级结论，如射影定理、角平分线定理、中线长定理等.教师除了亲自推导这些二级结论之外，还要选择合适的例题对这些结论加以使用，说明使用结论解题的优越性与局限性，同时达到授之以鱼与授之以渔的目的.