上拔力-水平力-扭矩组合荷载作用下斜桩承载特性模型试验

曹卫平， 石玉斌， 高帅鹏

(1.西安建筑科技大学 土木工程学院， 陕西 西安 710055； 2.陕西省岩土与地下空间工程重点实验室， 陕西 西安 710055)

1 研究背景

近年来，在桥梁、水上钻井平台及风力发电平台的群桩基础中，斜桩基础的应用颇具潜力，备受众多岩土工程师的关注[1-3]。在斜桩实际应用中，桩顶承受竖向荷载作用的同时，还要承受水平及扭矩荷载的组合作用，如风荷载作用下的输电塔塔架斜桩基础，在承担上部结构荷载的同时，还受到风力引起的水平及扭矩荷载的作用。斜桩基础四周土体的应力场分布与桩身轴线不对称，且桩顶所受水平荷载的方向往往不同于桩身倾斜方向，导致斜桩与直桩承载特性之间存在较大差异[4-6]，开展斜桩在组合荷载作用下承载特性的研究可以为工程应用提供理论支撑。

目前，关于斜桩承载特性的研究大多在单一荷载作用条件下进行，对组合荷载作用下斜桩的承载特性研究较少。曹卫平等[7-9]开展了室内模型试验，结果表明上拔荷载的作用会增加正斜桩的水平承载力，减少负斜桩的水平承载力。袁廉华等[10]开展了大型模型试验，证实了上拔荷载的存在对斜桩的水平刚度和极限承载力产生了消极作用。Hanna等[11]探究了斜桩在砂土中的竖向承载特性，结果显示斜桩在竖直方向上承载能力随桩身倾角的增大而减小。Meyerhof等[12]。研究了斜桩竖向承载特性规律，发现斜桩的倾斜角度越大，其竖向承载力越大，这与Sharma等[13]的研究结果相似，而与Hanna等[11]的研究结果相反。组合荷载作用下单桩承载特性的研究集中于直桩方面，且少有含扭矩荷载的研究。张磊等[14]基于室内模型试验，探讨了单桩在上拔及水平荷载作用下的承载特性，结果显示水平承载力随上拔荷载的增大先增加后减小。周俊鹏等[15]通过现场试验及数值模拟，发现上拔荷载与水平荷载大小的比例显著影响着桩身的承载特性。赵春风等[16]在砂土地基中进行了相关试验，证实竖向荷载的存在会增加单桩的水平承载力。江杰等[17]认为单桩在组合荷载作用下的承载力小于单一受荷桩，与邹新军等[18]的研究结果相似，而与赵春风等[16]的研究结果相反。郭沛翰[19]开展了竖向力、水平力及扭矩作用下单桩的承载特性模型试验，提出该3个荷载之间存在复杂的耦合关系，工程中不可通过叠加原理计算。

综上所述，目前对含扭矩的组合受荷斜桩承载特性的研究十分少见，且已有的研究结果也存在着差异，鉴于此，本文开展了室内模型试验，探讨了上拔、水平及扭矩荷载组合作用下的斜桩承载特性，并分析了各荷载与受扭斜桩承载特性之间的关系，可供工程应用参考。

2 模型试验设计

2.1 模型试验装置

试验所用模型槽的尺寸为160 cm×80 cm×120 cm(长×宽×高)，其主骨架由钢筋焊接而成，4个侧面由1 cm厚的钢化玻璃组合而成。

测量装置由3部分组成。位移的测量由位移计(量程30 mm)和量角器(量程180°)完成，在上拔荷载作用方向设置1个百分表测量桩顶上拔位移，水平荷载作用方向及与其垂直方向分别设置1个百分表测量桩顶水平位移，桩顶设置一个量角器测量桩顶扭转角；上拔及水平荷载通过设置在其荷载作用方向上的轴力传感器测量；应变由粘贴在桩身上的应变片及应变花测量，应变片对称粘贴在与水平荷载施加方向相同的桩身两侧，采用 1/4桥接用以测量弯拉应变，应变花对称粘贴在垂直于水平荷载施加方向上的桩身两侧，采用 1/2桥接用以测量剪切应变。模型试验装置如图1所示。

图1 模型试验装置示意图(单位：mm)

2.2 桩身及桩基试验材料

综合考虑几何相似比[20]原则及试验条件后，选取模型比尺为1∶15，从而确定模型斜桩外径D=40 mm，壁厚为3 mm，长度为1 100 mm，桩身由6061铝合金管制作而成，泊松比μ=0.33。在桩身外侧覆盖一层全树脂耐水砂布，并沿桩身每80 mm捆绑一圈细铁丝以增加桩侧摩擦力[21]和桩身的整体性。在桩顶钻一直径为6 mm的孔洞，用于对桩的定位和机械臂的安装。为避免桩内灌入砂土，桩端处用直径为40 mm的圆形玻璃进行封口处理。

试验所用桩基材料为中粗河砂，具体参数如表1所示。

2.3 模型试验方案

本次试验设计了4个工况，各工况具体试验方案见表2。表中Vu为斜桩的上拔极限承载力(N)，通过上拔荷载单独作用时的荷载试验求得。

表1 试验所用桩基土砂参数

表2 试验方案

2.4 模型试验步骤

首先填装底层砂土，厚度约为200 mm，用振动仪振动压密并整平砂面。填装完底层砂土后，用特定装置，通过桩顶孔洞，将模型桩固定到预定位置，然后继续分层填砂直至预设高度，每层相对密实度控制为0.72。

试验时，分别在桩顶施加相应工况的上拔荷载，桩顶竖向位移稳定后，记录下此时的桩顶位移和桩身应变作为初始读数。水平荷载的加载方式依据慢速荷载维持法，每级增加荷载20 N，根据规范[22]规定：荷载作用下桩顶的沉降速率不超过0.1 mm/h，且接连两次发生后便可进行下一阶段试验，当Q-s曲线开始陡升时、T-Ψ曲线开始陡升时或桩在砂土面处位移达到0.15D(桩外径)[16]时即终止加载。逐级荷载施加后每间隔5 min将桩顶位移记录下来，桩顶位移稳定后记录桩身应变。

同理,得出座椅处在4种不同车速下奇异值差分谱的关系,如图8所示.由图8中的值,可以确定在不同车速下奇异值的重构阶数.

3 结果分析与讨论

通过上拔荷载单独作用时的载荷试验，测得斜桩桩身倾角为15°和20°时的上拔极限承载力Vu分别为1 477、1 612 N。

图2为试验模型桩受组合荷载作用的等效示意图(水平荷载H和扭矩荷载T为桩顶所施加水平偏心荷载的等效荷载)，将斜桩桩顶的扭矩T(z方向)分解为T平行=Tcosα和T垂直=Tsinα(α为桩身倾角)。为便于表述，本文统一视水平荷载作用方向的土体为桩前土体(y方向)，相反方向为桩后土体(-y方向)；桩身倾斜方向的土体为桩右土体(x方向)，相反方向为桩左土体(-x方向)。由于本试验中桩顶水平荷载和扭矩荷载是通过力臂加载装置同时施加，故后文中所提到的水平荷载和扭矩荷载均为同步变化。

图2 试验斜桩桩顶受组合荷载等效示意图

3.1 组合荷载作用下桩顶水平位移的变化规律

模型桩在组合荷载作用下，x、y方向均会发生水平位移，由于x方向产生的位移很小，所以本文仅探讨y方向上的水平位移。

图3为各试验工况桩顶水平位移与水平荷载关系曲线。本文将桩顶在y方向的位移视为正，在-y方向的位移视为负。

由图3可以看出，在水平荷载和上拔荷载相同的条件下，桩身倾角的增加会导致水平位移的增加。从而证实了斜桩的水平承载力会受桩身倾角的影响，即随其增加而逐渐降低。分析其原因，桩前土体的水平反力影响了桩的水平承载力，上拔荷载存在的情况下，桩一侧土体受到扰动变得松散，另一侧远离桩身产生裂隙[15]。桩身承受扭矩发生位移时，桩前土体产生裂隙，从而减小了桩周土体的水平反力，导致水平位移增加。桩身倾角的不断增加导致桩与土体之间的裂隙不断增加，从而使水平位移增加。

3.2 组合荷载作用下桩顶扭转角的变化规律

图4为各试验工况桩顶扭转角与扭矩关系曲线。由图4可以看出，上拔荷载作用相同时，斜桩极限扭矩会受到桩身倾角的影响，随其增加而减小，如当桩顶上拔荷载为0.2Vu时，桩身倾角为15°比20°时的桩顶极限扭矩减小了17%。桩身倾角相同时，斜桩极限扭矩又会受到桩顶上拔荷载的影响，随其增加而减小，如当上拔荷载为0.6Vu时，15°和20°倾角桩体的极限扭矩较上拔荷载为0.2Vu时分别减少了5.26%和6.25%。

斜桩桩身倾角的增加会降低其极限扭转承载力。究其原因，桩侧摩阻力决定了桩顶极限扭矩的大小，而桩侧土压力决定了桩侧摩阻力的大小。在桩长相同且受荷作用一致的情况下，由于桩身倾角增加，其桩周覆土会变得更加松散。所以在相同工况下，倾角更大的斜桩的桩侧土压力更小，所能承受的极限扭矩更小。上拔荷载的增加会降低斜桩的极限扭转承载力。这是因为在斜桩桩顶施加上拔荷载后，桩左侧土体受到扰动变得松散，同时右侧土体远离桩身产生裂隙，桩右侧摩阻力大幅度减少，随着上拔荷载的增加，这种现象也更加显著。

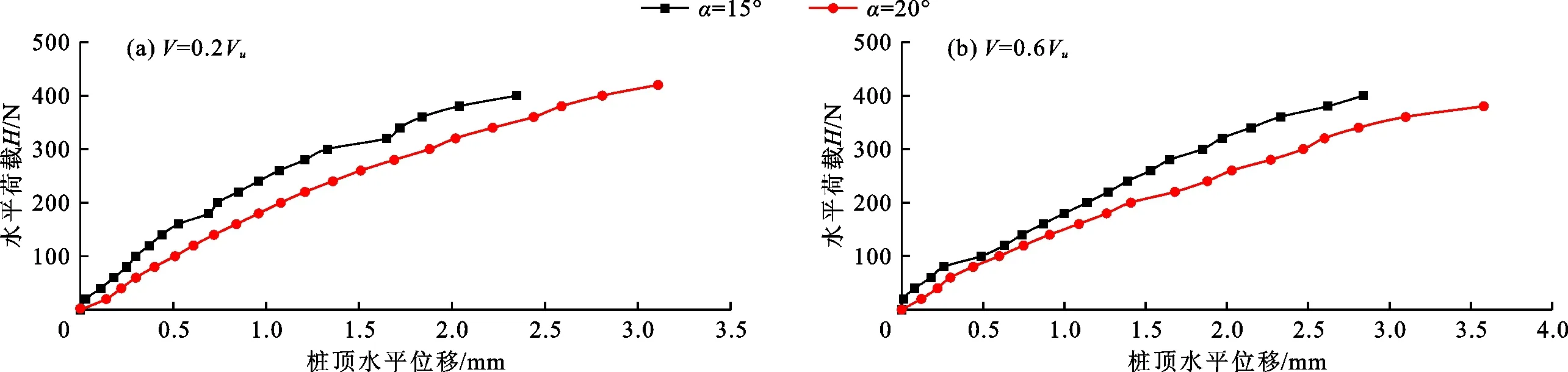
图3 各试验工况桩顶水平位移与水平荷载关系曲线

图4 各试验工况桩顶扭转角与扭矩关系曲线

3.3 组合荷载作用下桩身扭矩的变化规律

斜桩桩身砂土面以下的截面扭矩利用公式(1)计算。

Ti=GpWtΔεiTcos 45°

(1)

式中：Gp为斜桩的剪切模量，Pa；Wt为斜桩的抗扭系数，m3； ΔεiT为斜桩剪应变差值。

图5为各试验工况桩顶不同扭矩荷载下桩身扭矩与桩身相对深度关系曲线(图中Z为桩身深度，L为砂土中的桩身长度，下同)，图6为各试验工况桩身最大扭矩随桩顶扭矩荷载变化曲线。从图5可看出，桩身扭矩随着桩身相对深度的增加呈现出先增加至峰值再逐渐减少到趋近于0的变化趋势；桩身倾角逐渐增加的过程中，桩身扭矩最大值所在截面位置逐渐远离桩顶，如倾角为15°的斜桩在Z/L=0.16处达到桩身最大扭矩，倾角为20°的斜桩在Z/L=0.26处达到桩身最大扭矩。对比图5(a)与5(c)可以看出，同样为15°倾角的斜桩，当上拔荷载为0.6Vu时，桩身扭矩最大值出现在Z/L=0.17处，而当上拔荷载为0.2Vu时，桩身扭矩最大值出现在Z/L=0.16处，相对深度仅相差0.01。

从图6可以看出，上拔荷载作用相同时，桩身扭矩最大值会受到桩身倾角的影响，并随其增加而增加，如上拔荷载为0.2Vu、扭矩荷载T为36.00 N·m时，桩身倾角为15°的斜桩桩身扭矩最大值为37.08 N·m，20°的斜桩桩身扭矩最大值为62.10 N·m，增加了67.48%。桩身倾角恒定时，桩身扭矩最大值会受到桩顶上拔荷载的影响，并随其增加而增加，如当桩身倾角为15°，桩顶扭矩荷载为36.00 N·m时，上拔荷载0.6Vu作用下的桩身扭矩最大值为47.74 N·m，相较于上拔荷载0.2Vu作用下的桩身扭矩最大值37.08 N·m增加了28.75%。

上述结果表明，桩身倾角和桩顶上拔荷载的增加会降低斜桩抗扭性能。斜桩桩身扭矩最大值所处位置不会受到上拔荷载的影响，但会受到桩身倾角的影响，随其增加而下移。

3.4 组合荷载作用下桩身弯矩的变化规律

组合荷载作用下，斜桩桩身弯曲变形会同时发生在x和y两个方向上，本文仅研究y方向上的桩身弯曲变形。斜桩桩身砂面以下的截面弯矩利用公式(2)计算。

(2)

式中：EpI为斜桩抗弯刚度，N·m2； Δεi为斜桩弯拉应变片之间的差值；d为试验所用桩的内径，m。

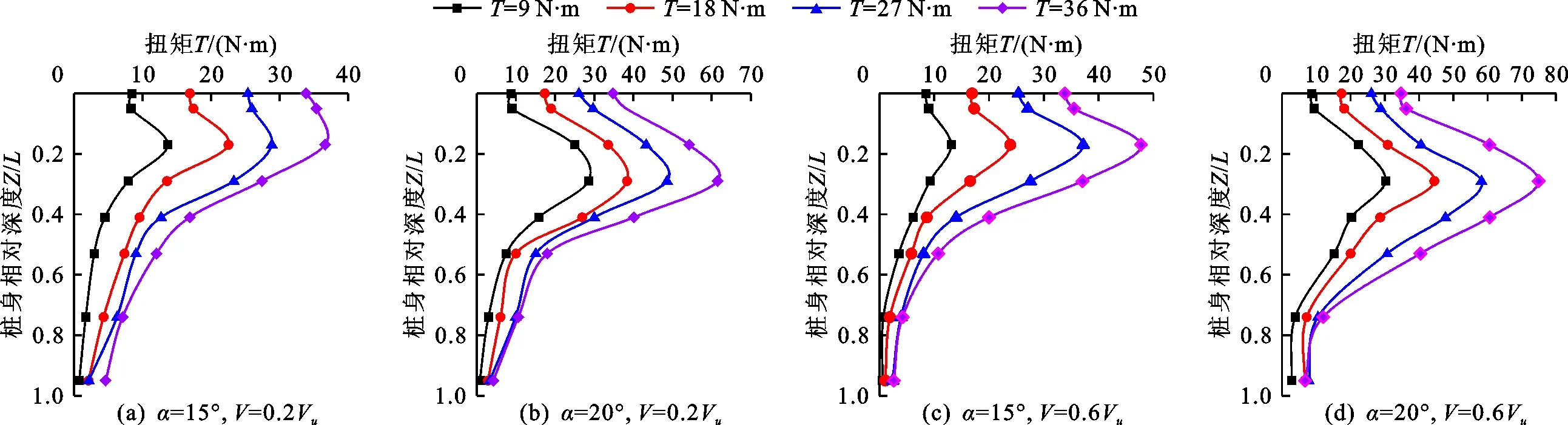
图5 各试验工况桩顶不同扭矩荷载下桩身扭矩与桩身相对深度关系曲线

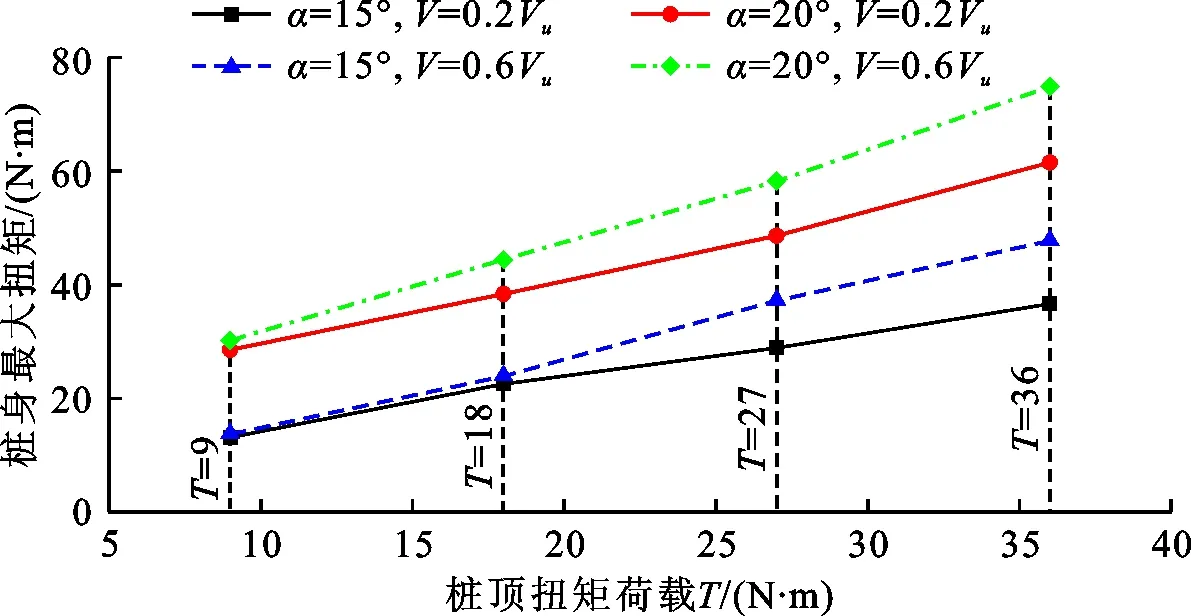
图6 各试验工况桩身最大扭矩随桩顶扭矩荷载变化曲线

图7为各试验工况桩顶不同扭矩荷载下桩身弯矩与桩身相对深度关系曲线，图8为各试验工况桩身最大弯矩随桩顶扭矩荷载变化曲线。由图7、8可以看出，不同倾角斜桩桩身的弯矩随桩身相对深度呈现出的变化趋势相似， 即桩身弯矩随着桩身相对深度的增加呈现出先增加至峰值再逐渐减少到0或趋近于0的变化趋势。上拔荷载和扭矩荷载作用相同时，桩身弯矩的最大值会受到桩身倾角的影响，随其增加而增大，如当桩顶上拔和扭矩荷载分别为0.2Vu和36.00 N·m时，15°斜桩桩身弯矩的最大值为47.44 N·m，而20°斜桩则为55.43 N·m，相比增加了16.84%。桩身倾角及扭矩荷载作用相同时，桩身最大弯矩会受到桩顶上拔荷载的影响，随其增加而增大，如当桩顶扭矩荷载为27.00 N·m时，15°斜桩在0.2Vu桩顶上拔荷载作用下桩身弯矩的最大值为33.75 N·m，在0.6Vu桩顶上拔荷载作用下桩身弯矩的最大值为38.33 N·m，相比增加了13.57%。不同上拔荷载作用下，各角度桩均在Z/L=0.17处达到桩身最大弯矩。

图7 各试验工况桩顶不同扭矩荷载下桩身弯矩与桩身相对深度关系曲线

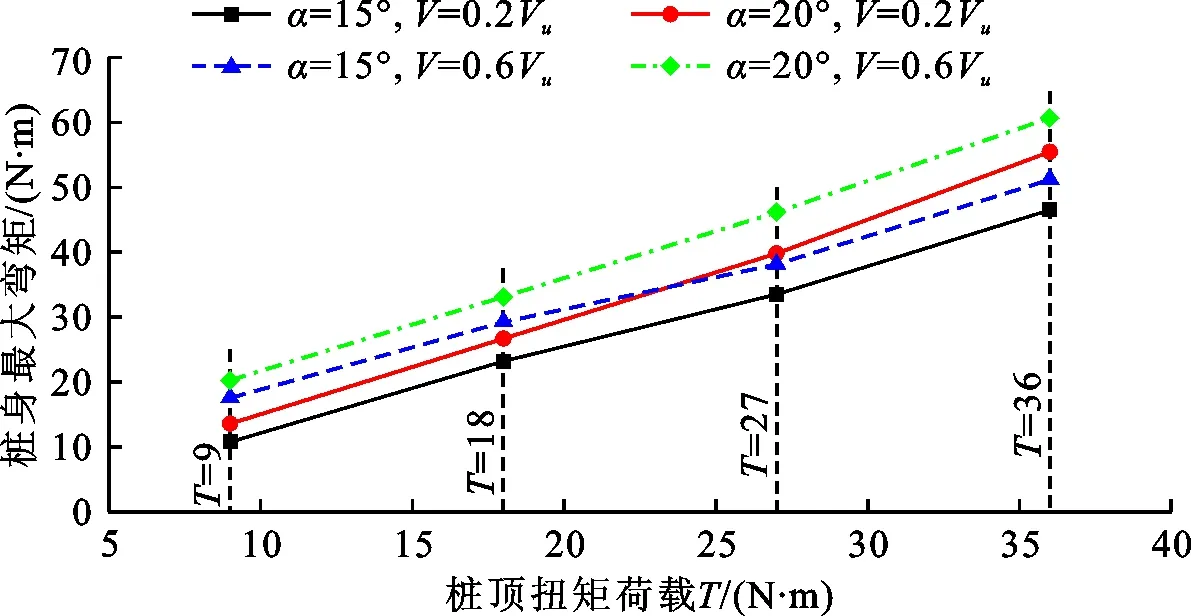
图8 各试验工况桩身最大弯矩随桩顶扭矩荷载变化曲线

上述结果表明，斜桩承受组合荷载时，荷载的传递只存在于一定的深度范围，且该深度随上拔荷载的增大而加深，与邹新军[23]等的研究结论相似。斜桩桩身最大弯矩所处位置是固定不变的，与桩顶上拔荷载和桩身倾角没有显著关系，但其大小会随桩顶上拔荷载和桩身倾角的增大而增大。

4 结 论

通过室内模型试验，探讨了斜桩桩顶受到上拔、水平及扭矩荷载组合作用下斜桩的承载特性，得出以下结论：

(1)水平及上拔荷载相同的条件下，桩身倾角的增大会加强斜桩的水平承载能力。

(2)桩身倾角以及桩顶上拔荷载的增加会加强斜桩的扭转承载能力。斜桩桩身扭矩最大值所在位置与桩身倾斜角度有关，随其增加而下移。斜桩抵抗扭矩荷载的能力随桩身倾斜角度以及桩顶上拔荷载的增大而减小。

(3)桩身倾斜角度以及桩顶上拔荷载的增大会提高斜桩桩身弯矩的最大值，但其所处的位置与桩身倾斜角度以及桩顶上拔荷载无关，该位置总是位于Z/L=0.17处。