基于指标优选和模糊综合优化模型的地下水质量评价研究

王 敬， 袁星芳， 韩 忠， 黄林显， 梁 浩， 邢立亭， 侯金霄

(1.山东省第六地质矿产勘查院， 山东 威海 264209； 2.济南大学 水利与环境学院， 山东 济南 250022； 3.山东省地下水数值模拟与污染控制工程技术研究中心， 山东 济南 250022； 4.山东省国土空间生态修复中心，山东 济南 250014)

1 研究背景

地下水是人类生活和工农业生产的主要水源，同时也是生态环境的重要控制因素[1-2]。随着人类社会的快速发展，地下水污染问题已经变得越来越严重[3-4]。地下水质量评价可以准确识别地下水污染的时空分布状况，能够为地下水资源的保护和开发提供科学依据。当前应用较多的地下水质量评价方法主要包括单因子评价法[5]、内梅罗指数法[6]、灰色模型法[7]、主成分分析法[8]、神经网络法[9]、物元可拓法[10]和模糊综合评价法[11]等。单因子评价法和内梅罗指数法评价过程简单、易于操作，但过于突出超标最大指标的影响且未考虑不同指标间的权重因素；灰色模型法具有对数据要求低且计算量小的特点，但其无法充分考虑系统的随机性，造成评价结果的分辨率较低；层次分析法指标权重的确定主要取决于人的主观经验，使得评价结果不够科学；神经网络法需首先依靠其他评价方法生成大量样本数据进行训练，并且其模型的构建过程过于复杂。

此外，传统的地下水质量评价方法在水质等级划分时大多存在“非此即彼”的问题，使得评价结果笼统且不准确。而模糊数学评价法由于能够很好地解决水质评价中等级划分的不确定性问题而得到了广泛应用[12]。张晓叶等[13]分别利用F值法、内梅罗指数法和模糊综合评价法对北京市某地枯水期地下水质量状况进行了评价，结果表明模糊综合评价法能够充分考虑不同水质等级之间的过渡，数据连续性更好，其评价结果也更加准确合理。但是，传统的模糊数学评价法往往需要较多的水质指标，一方面增加了采样与检测成本，另一方面不同指标间的高相关性会造成数据冗余，引起评价过程中的重复描述，导致评价结果偏大或偏小。近年来，指标优选类方法由于能够有效消除指标间存在的数据冗余和叠加问题，实现评价指标体系的独立性和简明性而得到了广泛应用[14]。其中，周星宇等[15]采用主成分分析法对河流水文改变指标进行了优选，结果表明运用优选指标对河流水文情势变化进行评价能够大大减少传统水文指标改变法中的评价目标，且具有较高的精度；邱庆泰等[16]构建了基于指标区间优选法的评价模型并对邹城市水资源配置方案进行了论证，证明优选评价模型实用性更加显著。

但是，已有指标优选的研究大多集中在地表水文特征的分析，缺少在地下水质量评价中的应用，特别是较少涉及到同时考虑指标相关性和主控性的研究。基于此，本文分别利用Pearson相关系数(相关性)和因子分析(主控性)对水质评价指标进行优选，在此基础上结合模糊综合优化模型对2017年寿光市枯水期地下水质量状况进行评价，以期能够为未来地下水质量评价的研究提供一定的参考，同时为寿光市地下水资源的管理保护和开发利用提供科学依据。

2 数据来源与研究方法

2.1 研究区概况

寿光市行政区划属潍坊市，位于山东半岛中部，其北部与莱州湾相邻。寿光市工农业用水主要来源于地下水，多年的持续开采造成区内地下水超采严重。此外，寿光市还是我国主要的蔬菜生产基地，蔬菜种植过程中化肥的过度使用引起地下水污染日益严重，水质状况持续恶化。因此，对寿光市地下水污染现状及其污染风险进行准确评价极为重要。

2.2 数据来源

利用寿光市2017年5月6日13口监测井的13组地下水水样进行研究(监测井位置如图1所示)。

图1 研究区监测井位置分布图

研究范围涉及pH、氯化物、氨氮、硝酸盐、COD、溶解性总固体、铁和锌等36项水质指标，各指标界限及等级划分均依据《地下水质量标准》(GB/T 14848—2017)中的相关规定进行[17]。根据研究区地下水污染现状，综合考虑不同指标对当地水质的实际影响，选取锌、氯化物、硫酸盐、硝酸盐、COD、总硬度和溶解性总固体共7个主要影响当地水质的污染指标作为原始评价指标，各主要指标统计值如表1所示。

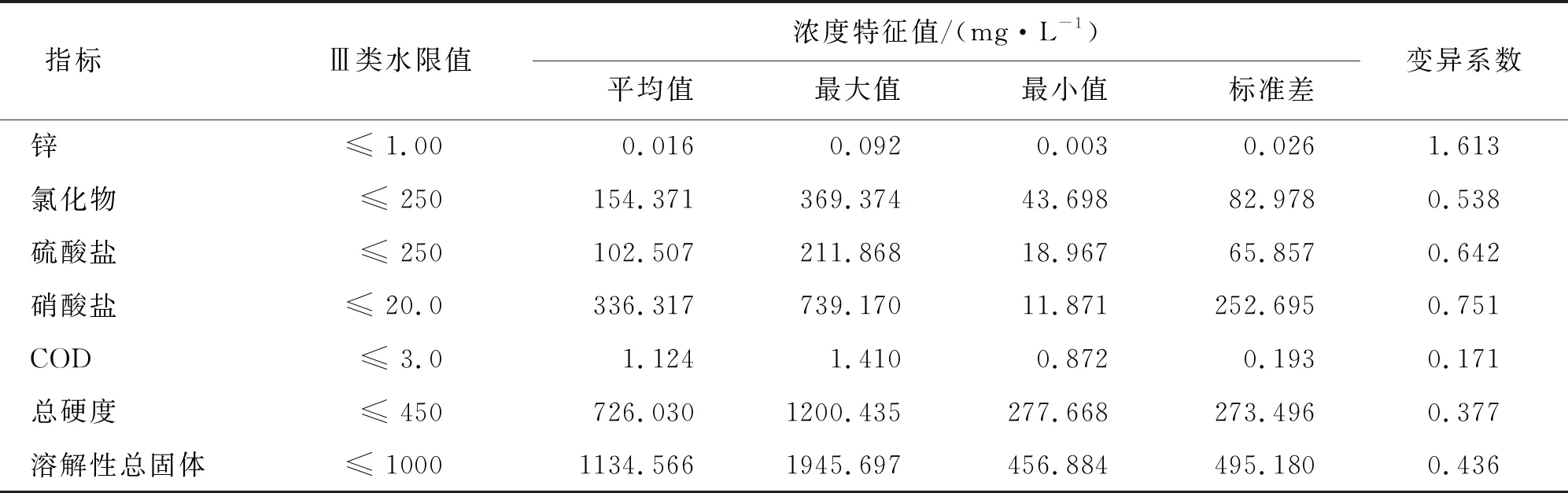
表1 地下水水样主要指标统计值

通过表1可以看出，研究区硝酸盐、总硬度和溶解性总固体超标较为严重，其浓度平均值均超过《地下水质量标准》(GB/T 14848—2017)中Ⅲ类水的限值，说明研究区地下水受农业种植污染严重且硬度较高；除COD外，锌、氯化物、硫酸盐、硝酸盐、总硬度和溶解性总固体的变异系数均较大，说明研究区内的水质空间分布变化较大，存在局部污染物富集的高污染地区；此外，锌的变异系数最大，达到1.61，说明研究区内局部地区该离子含量偏高，可能是潜在的污染源。

2.3 研究方法

进行地下水质量评价时如使用较多的水质指标，不但会造成取样和检测成本的增加，且不同指标间的高相关性会引起数据冗余，使模型的泛化能力和评价精度下降。本次研究利用Pearson相关系数法(Pearson correlation coefficient)和因子分析法(factor analysis)对水质评价指标进行优选，剔除冗余指标，提取主控指标，实现评价指标体系的独立性和简明性；同时，采用模糊综合优化模型分别对原始指标和优选指标进行评价，由此验证该指标优选方法的准确性和合理性。其中，指标优选及地下水质量模糊综合优化评价均在python编程环境中实现。

2.3.1 指标优选方法

(1)Pearson相关系数。Pearson相关系数由卡尔·皮尔逊提出，主要用来度量两个变量之间的相关性程度。Pearson相关系数已被广泛应用于不同领域，并已被证明是一种进行相关性分析的有效方法[18]。其计算公式如下：

(1)

(2)因子分析[19]。因子分析是一种从变量组合中提取共性因子的统计技术。该分析方法能够在不损失主要信息的前提下从不同水质指标中寻找相互独立的变量，并将其归结为数量较少的几个主控因子，且能保留水质影响因素的绝大部分信息。其计算公式如下所示：

Xji=aj1f1i+aj2f2i+…+ajifji+djuji

(2)

式中：fji为适用于所有变量的公因子；uji为适用于每一个变量的唯一因子；aji为因子负载系数；dj为标准回归系数；Xji为fji与uji的线性组合。

2.3.2 模糊综合优化模型 地下水质量评价涉及到多个指标、多个等级，且通常以区间形式来表示划分标准，造成在进行水质指标界限和等级划分时存在着较大的不确定性和模糊性[20]。模糊综合优化模型耦合模糊综合评价法和可变模糊集法，通过建立相对隶属度函数能够有效解决划分标准区间值对评价结果的影响，可以很好地对水质类别的模糊性进行描述。

(1)设待评价样本集共有n个水质样本，每个样本包含m个指标，则其特征值矩阵可以定义为：

X=(xji)

(3)

式中：xji为第j个水质样本的第i个指标的特征值，i=1, 2, …,m；j=1, 2, …,n。

Iab=([a,b]ih)

(4)

本文按照《地下水质量标准》(GB/T 14848—2017)划分为5个等级，即f=5；a，b分别为指标i在第h等级浓度范围的下限值和上限值。

(3)根据标准值区间矩阵Iab建立评判等级范围域矩阵Icd：

Icd=([c,d]ih)

(5)

式中：c为指标i在第h-1等级浓度范围的下限值；d为指标i在第h+1等级浓度范围的上限值。

(4)确定指标i对等级h的M矩阵：

M=(Mih)

(6)

公式(6)中M为[a,b]中相对隶属度等于1的点，其计算方法可参考文献[11]。评价指标浓度实测值x及M与[a,b]、[c,d]的位置关系如图2所示。

图2 点x、M与[a, b]、[c, d]的位置关系

(5)计算相对隶属度矩阵

2014年，湖南水利将乘党的十八届三中全会的春风，继续在水利发展的欢腾盛世下锐意进取，以深化改革为主线，强基础、抓管理、争项目、提质量，大力推进安全水利、民生水利、生态水利，加快建立人水协调的现代水利体系，促进水利科学发展，服务四化两型建设。以更饱满的激情、更广阔的视野、更开放的姿态为水利事业的蓬勃发展和湖南的加速崛起作出更大的贡献。

当x在M点的左侧时，其相对差异函数为：

(7)

当x在M点的右侧时，其相对差异函数为：

(8)

式中：β为非负指数，一般取β=1；通过以下公式计算得到相对隶属度矩阵：

μA(u)=(1+DA(u))/2

(9)

(6)确定水质指标的权重向量ωi。指标权重的合理确定对水质评价至关重要，其直接影响评价结果的合理与否。目前常用的权重确定方法有比例法、首尾比率法、超标法、专家打分法、灰色聚类法和熵值法等。本次研究采用熵值法确定水质指标的权重[20]。

(7)计算每个水质样本对级别h的综合相对隶属度向量：

(10)

其中α和p的值通常取1。利用下式对向量进行归一化：

(11)

(8)计算综合级别特征值：

(12)

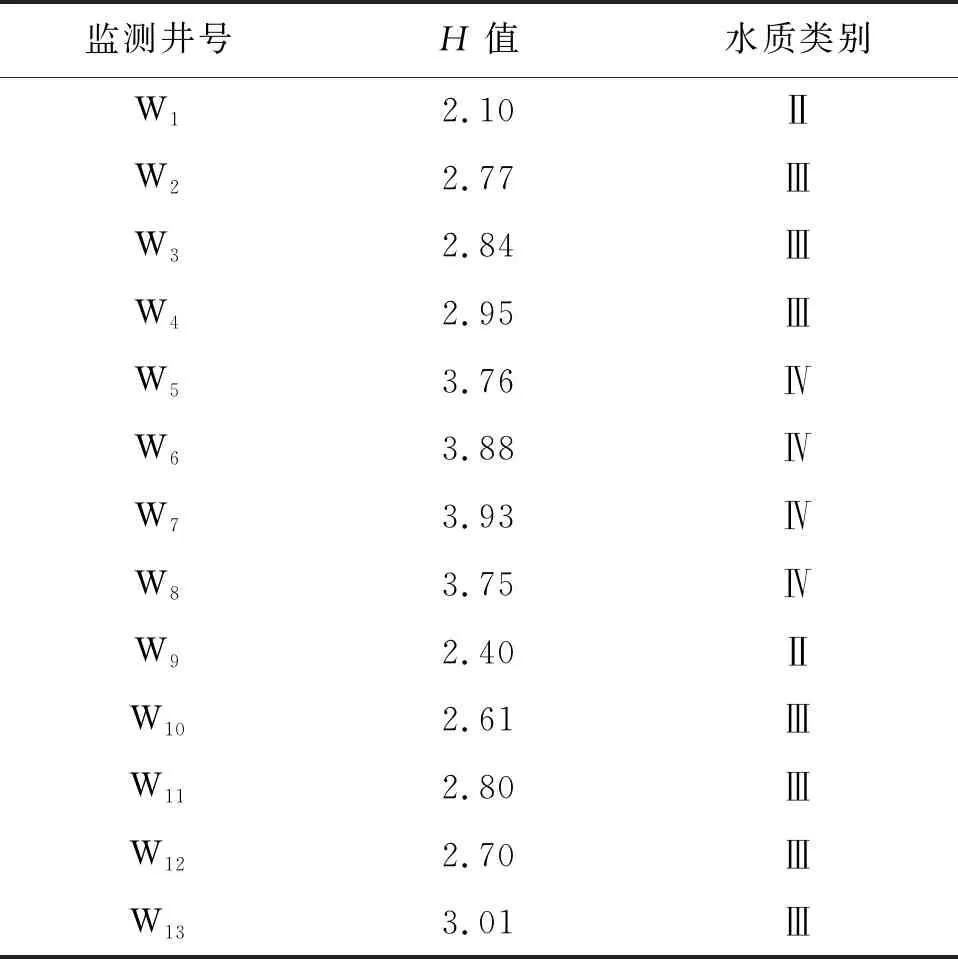
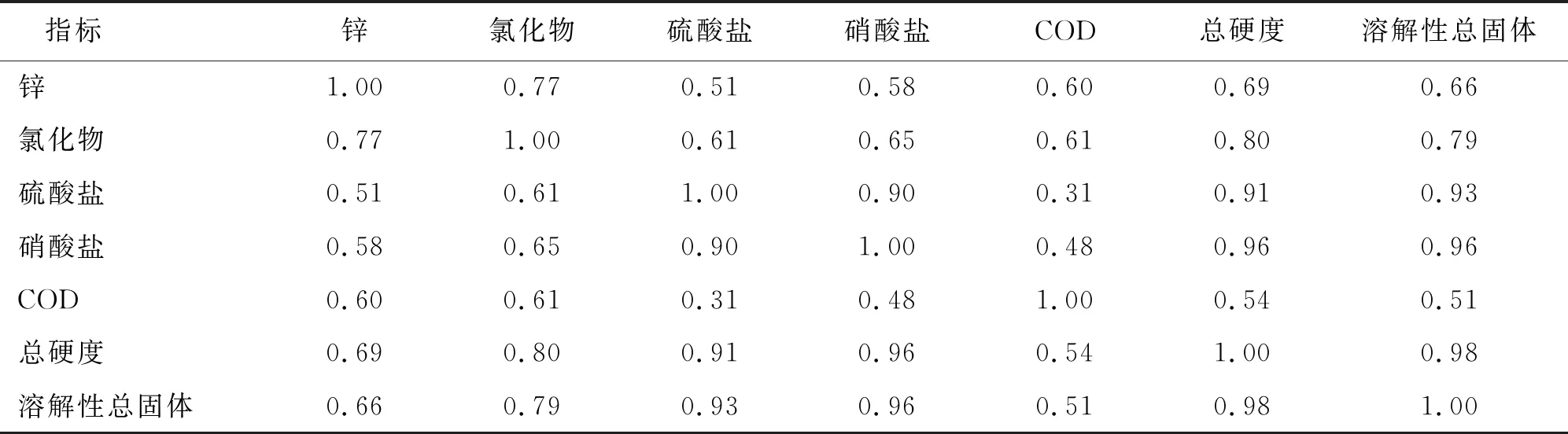
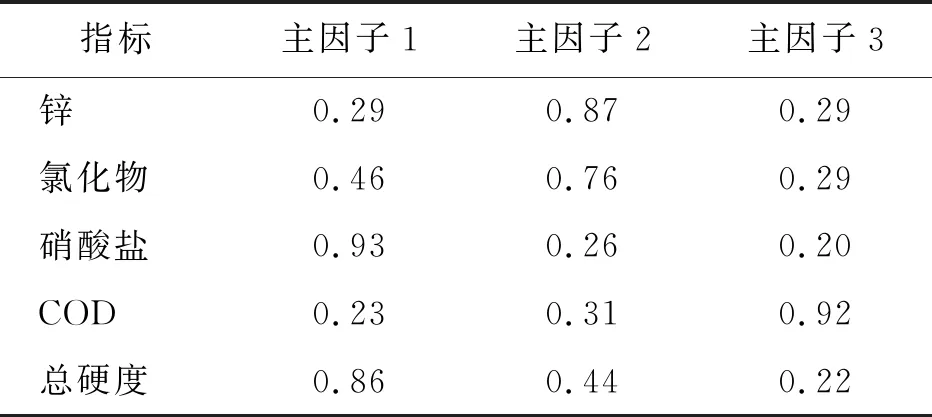
(9)根据综合级别特征值H对水质样本进行水质等级划分：如果1

3 结果与分析

3.1 原始指标评价结果

利用选取的锌、氯化物、硫酸盐、硝酸盐、COD、总硬度和溶解性总固体7个主要影响当地水质的原始指标通过模糊综合优化模型进行地下水质量评价，评价结果如表2所示。

表2 研究区原始指标地下水质量评价结果

由表2可以看出，监测井W1-W4、W9-W13的地下水质量等级均为Ⅱ或Ⅲ类，说明这些区域水质状况相对良好；监测井W5-W8分布于寿光市中南部，地下水质量等级均为Ⅳ类，反映出水质状况较差，其主要超标因子为硝酸盐和总硬度。分析其原因主要是由于该区域含水层岩性以中砂、粗砂以及砾石为主，含水层渗透性强，且地下水埋深较浅，含水层比较容易受到地表污染物的下渗污染；同时，该区域是寿光市主要的蔬菜种植区，蔬菜种植过程中氮肥的过度使用造成大量氮肥进入地下水造成污染。此外，研究区中总硬度还呈现出随河流流向不断增加的趋势，主要是研究区内地下水普遍接受河水补给，地表污染物通过河流进入地下水含水层逐渐累积的结果。

3.2 Pearson相关系数指标优选评价结果

利用Pearson相关系数对选取的锌、氯化物、硫酸盐、硝酸盐、COD、总硬度和溶解性总固体7个指标进行优选，各指标相关性分析结果如表3所示。

表3 研究区各水质指标的相关系数

通过表3可以看出，硫酸盐、硝酸盐、总硬度和溶解性总固体4个指标具有较强的相关性，其相关系数r均在0.9以上。指标间的高相关性会造成数据冗余，引起评价过程中的重复描述，造成模型的泛化能力和评价精度下降。由于硝酸盐和总硬度在研究区中超标较为严重，因此剔除硫酸盐和溶解性总固体两个指标，优选后的指标为锌、氯化物、硝酸盐、COD和总硬度5个指标。利用模糊综合优化模型进行评价，得出的各监测井水质样品原始指标与优选指标H值如图3所示。

图3 研究区各水质样品原始指标和Pearson优选指标H值

由图3可以看出，采用原始指标和Pearson优选指标进行模糊综合评价的结果基本一致：13个监测井样品水质等级的划分完全一致，综合级别特征值H有一定的差别，但差别均较小。经计算，优选指标的综合级别特征值H相对于原始指标的变动范围介于1.8%～9.4%之间，并且在2%～4%之间的分布更为集中，说明两者非常接近。此外，由于优选指标剔除了高相关性指标的叠加影响，因此其评价结果也更加合理。比如监测井W5原始指标中总硬度和溶解性总固体的浓度分别为1 076.74和1 946 mg/L，从Pearson相关系数可知这两个指标的相关性达到98%(属于高度相关)，造成两个指标在评价过程中被重复描述，导致综合级别特征值H略微偏大。所以，优选指标可以有效减少指标高相关性所带来的数据冗余问题，且能够保留原始指标的有用信息，评价结果也更加合理。

3.3 因子分析法指标优选评价结果

Pearson相关系数分析的主要目的是剔除相关性较高的水质指标，减少水质指标之间的相关性。因子分析法则主要是从优选后相关性减弱的水质指标中(锌、氯化物、硝酸盐、COD和总硬度)进一步优选出能反映原始指标绝大部分信息的主控性公因子。为了保证所提取的公因子具有较强的代表性，其累积贡献率应大于75%。首先利用sklearn机器学习库中的因子提取算法验证特征值和累积贡献率随所提取公因子数量增加的变化情况，结果如图4所示。

由图4可以看出，特征值随着所提取因子个数的增加而减小，而累积贡献率则不断增加；累积贡献率在前3个因子时增加速率较快，但从第4个因子起增加速率开始变缓；其中，前3个因子的累积贡献率达到95%，能够保证所提取的公因子有较强的代表性。因此，共提取3个公因子，并将因子荷载矩阵进行正交旋转，结果如表4所示。

图4 因子分析的特征值和累积贡献率

表4 旋转因子荷载矩阵

由表4可以看出，硝酸盐和总硬度在主因子1有较大值，表明硝酸盐和总硬度与主因子1密切相关，反映了农业种植产生的营养盐类物质对水质的影响；锌在主因子2有较大值，表明锌与主因子2密切相关，反映了农药喷洒产生的有毒重金属对水质的影响；而COD在主因子3有较大值，表明COD与主因子3密切相关，反映了生活污水引起的有机污染对水质的影响。因此，可以确定主控因子为硝酸盐、总硬度、锌和COD 4个指标，利用模糊综合优化模型进行评价，结果如图5所示。

图5 研究区各水质样品原始指标和不同方法优选指标H值

由图5可见，在进一步剔除氯化物后采用原始指标和Pearson+因子分析法优选指标进行评价的结果同样基本一致：13个样品水质等级的划分只有监测井W5不一致(原始指标划分的等级为Ⅳ类，Pearson+因子分析法优选指标划分的等级为Ⅲ类)；综合级别特征值H有一定的差别，Pearson优选指标+因子分析法计算的特征值H相对于原始指标的变动范围介于1.2%～10.8%之间，并且在1%～6%之间的分布更为集中，说明两者差别较小。对于监测井W5来说，虽然Pearson+因子分析法优选指标将其评价为Ⅲ类水，但其综合级别特征值H仅由原始指标的3.76减小为优选指标的3.35(Ⅲ类水与Ⅳ类水的特征值H界限为3.5)，变动幅度较小。分析其原因，虽然氯化物的浓度较高，为339.37 mg/L，接近Ⅳ类水浓度范围的上限值，但氯化物为研究区的非主控指标，所以将其剔除后对综合级别特征值H的计算结果影响较小。

4 讨 论

(1)通过前面的分析可以看出，指标优选方法能够删除信息重复性指标并提取主控性指标，有效缩减了评价指标的数量。如文献[11]和文献[12]分别采用了11项和9项指标对研究区地下水质量进行评价，而本研究通过指标优选采用4项指标即可做出合理的评价，因此有效减少了采样与检测成本。

(2)指标优选方法能够有效解决由于评价信息重复描述而导致评价结果偏大或偏小的问题，使得评价结果更加合理。如研究区监测井W5原始指标中总硬度和溶解性总固体两个指标的相关性达到98%，导致其综合级别特征值H评价值偏大，而优选指标可以有效减少指标高相关性所带来的数据冗余问题，评价结果也更加合理。

(3)此外，通过因子分析法提取出研究区地下水质量的主控指标，可以准确识别出研究区地下水污染的主要影响因素，能够为地下水资源的保护和治理提供科学依据。

5 结 论

(1)地下水质量评价是一个涉及到多指标、多等级且考虑区间值的模糊评价问题，通过将模糊综合评价和可变模糊集耦合，能够很好地解决评价过程中指标界限和水质等级划分的不确定性和模糊性问题，数据连续性更好，其评价结果也更加准确合理。

(2)通过利用Pearson相关系数剔除高相关性指标并利用因子分析提取出主控性指标，将7个原始水质评价指标优选为4个指标，不但能够有效减少数据冗余，而且能够充分保留原始指标的有效信息，具有更高的评价合理性；在此基础上，进一步识别出研究区地下水污染的主控指标为硝酸盐、总硬度、锌和COD，为了防止研究区地下水污染的进一步恶化，要加大对这4个指标的监控力度。

(3)评价结果显示，研究区除W5～W8监测井外，其他监测井的地下水质量等级均为Ⅱ或Ⅲ类水，说明这些区域水质状况相对较好；W5～W8监测井的地下水质量等级为Ⅳ类水，其主要超标因子为硝酸盐和总硬度，主要是蔬菜种植过程中氮肥的过度使用及地表污染物通过河流进入地下水体逐渐累积的结果，因此要进一步加强对蔬菜种植污染排放及河流水质的监测和控制。

(4)高昂的取样传感器成本是地下水质量实时监控系统建立的一个主要阻碍，而通过优选指标则可以减少取样传感器的安装数量，大大减少取样成本。下一步的研究重点是利用优选指标建立寿光市地下水质量实时监控系统，对寿光市地下水水质状况进行实时评价和预测，为寿光市地下水资源的开发利用和管理保护提供科学依据。