表面微沟槽对风力机翼型气动性能的影响研究

牛志罡， 罗大海， 王子尧

(1.上海理工大学 能源与动力工程学院，上海 200093； 2.上海市动力工程多相流动与传热重点实验室，上海 200093)

风力机风能利用效率与其翼型的气动性能密切相关，研究风力机翼型的减阻特性对增大风力机的输出功率具有重要意义[1]。传统观念认为阻力大小一般与物体表面的粗糙度成正比，但随着湍流理论的蓬勃发展，这一传统认知被打破，仿生减阻展现出极大的优势[2]。仿生减阻是指研究鲨鱼、海豚等运动较快动物的表面结构，从而设计表面沟槽几何特征，使壁面流场重新分布，达到减小摩擦阻力的目的[3-4]。

王晋军[5]开展了不同粗糙度沟槽的试验研究，结果发现减阻大小与沟槽深度和宽度有关。陈莹等[6]在旋成体模型表面粘贴铝基沟槽蒙皮，选定3种尺寸的沟槽进行减阻试验，发现与光滑表面相比可减小约3%～4%的阻力，并得出计算沟槽无量纲高度和宽度的公式。张子良[7]提出了沟槽模化方法，探索二维V型沟槽表面的流场特性及其减阻机理，研究表明最大减阻率可达3.07%。徐琰等[8]利用边界层理论提出一套减阻微沟槽的高度设计方法，得出三角形锯齿微沟槽的减阻率达5.5%；进行减阻沟槽设计时深度为主要因素，保持在y+=14左右具有较好的减阻效果。叶学民等[9]对锯齿尾缘叶片进行数值模拟，探究了3种不同长度的锯齿尾缘对风机的性能影响，在小流量工况下提高了风机的效率也改变了动叶尾缘脱落涡的结构。陈璠等[10]基于仿生学结构对不同沟槽布局形式在不同雷诺数下的减阻效果开展了对比研究，结果显示，横向和纵向布局时沟槽减阻率均随雷诺数增大而减小，且雷诺数影响占主导地位。国外对沟槽减阻技术的研究起步较早，美国国家航空航天局兰利研究中心发现顺流向的微小沟槽表面能有效地降低壁面摩阻，由此引发了表面沟槽减阻技术的研究热潮。早期开展的是沟槽平板湍流减阻研究，研究人员发现最佳的沟槽设计形式为对称的V型沟槽，且当其沟槽深度h和沟槽间距s的无量纲尺寸h+≤25和s+≤30时具有减阻效果[11-12]。Chamorro等[13]将不同形式和尺寸的沟槽布置在机翼表面并分析得出沟槽尺寸的无量纲值对阻力系数的影响，沟槽的尺寸h+=8和s+=15时减阻效果最佳。Timmer等[14]对荷兰代尔夫特理工大学设计的翼型进行了气动分析，并研究了Z字型沟槽对DU96-W-180翼型升阻力特性的影响。Sareen等[15]在3种雷诺数情况下对DU96-W-180翼型表面V型沟槽进行了减阻实验，测得最优沟槽尺寸为62 μm时可以达到5%的减阻效果。Radmanesh等[16]在NACA S5020翼型表面布置矩形沟槽，进行了数值模拟研究，发现减阻效果在很大程度上取决于攻角，非优化的沟槽在某些攻角下反而增加了4%的阻力。

目前，国内外关于翼型表面仿生沟槽的研究主要采取实验和二维数值模拟的形式，而较少采用三维模型通过数值模拟来研究表面沟槽的减阻效应。在以往针对翼型的数值模拟中，沟槽大多采用垂直来流方向的横向布局形式，为了减少计算量，往往采用二维数值模拟，这种简化模拟得到的研究结论并不适用于沟槽顺来流方向的纵向布局情形。笔者采用三维数值模拟来研究沟槽纵向布局时对风力机翼型气动性能的影响，通过系统分析不同工况下翼型的升阻力特性及表面摩擦力系数来阐述表面沟槽的减阻机理。

1 数值方法和几何模型

基于Ansys Fluent商用计算流体动力学(CFD)软件对风力机翼型绕流流场进行三维定常不可压雷诺平均方法(RANS)模拟。速度压力耦合采用SIMPLE算法，压力项和动量项空间离散采用二阶迎风格式，同时考虑翼型表面的流动转捩，选用基于γ-Reθ t模型[17]的四方程Transition SST模型。3种不同翼型的几何轮廓对比如图1所示，其中x、y分别为弦向和纵向坐标,c为翼型弦长。

图1 翼型几何轮廓对比

本文重点考虑DU96-W-180翼型，并选用相对厚度接近的S809翼型及同等厚度的NACA0018翼型进行对比。对于翼型表面微沟槽，考虑L型和V型2种几何形式，如图2所示。其中，w为L型沟槽宽度。

(a) L型沟槽

(b) V型沟槽

沟槽深度和间隔对应的无量纲几何参数[11-12]定义如下：

h+=h·u*/ν

(1)

s+=s·u*/ν

(2)

(3)

式中：τω为壁面剪切应力；ν为流体运动黏度；ρ为流体密度。根据文献[18]，表面沟槽减阻特性曲线可分为黏性区(h+=0～<11)、减阻效果恶化区(h+=11～25)和粗糙表面区(h+>25)，应尽量确保沟槽在最佳减阻点(h+=11)附近。本研究中仅改变h和s，沟槽几何特征保持不变，计算公式详见文献[6]。

布置表面微沟槽的仿生翼型三维几何模型、L型和V型沟槽三维模型，如图3所示。沟槽顺流向纵向布置，覆盖翼型的上下表面。由于沟槽非常微小，内部的网格尺度也很微小，考虑到计算量，沿翼型展向均匀布置10个沟槽。

(a) 仿生翼型三维几何模型

计算域和网格分布如图4所示，其中α为来流攻角。远离翼型的计算域采用O型网格，如图4(a)所示；翼型附近的计算域采用C型网格，如图4(b)所示。外边界距翼型表面约为60倍翼型弦长，尽量减小外边界对内部流场的影响。外边界左侧为速度进口边界，右侧为压力出口边界，计算域展向两侧设为对称边界条件，翼型表面设置为无滑移绝热固壁。

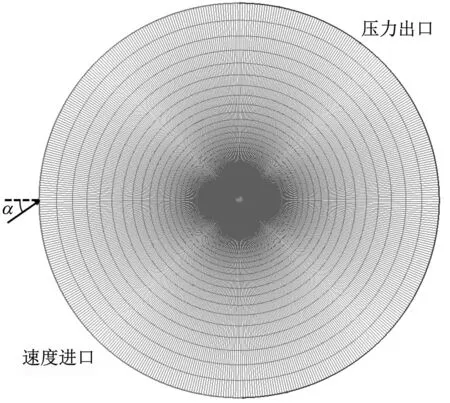
(a) 全局网格

沟槽附近的网格分布如图5所示。L型沟槽内部设置至少4个网格单元，V型沟槽内部设置至少8个网格单元。从沟槽内部区域到边界层外部流场区域，采用多块结构化搭接网格，网格分布由密到疏，以保证沟槽附近流场求解精度，同时减少总体计算网格数。

想困惑，从十个方面揭示出《共产党宣言》的时代价值和当代生命力，力图帮助读者特别是当代中国共产党人牢固树立共产主义远大理想，补足“精神之钙”。

(a) L型沟槽

为了检验计算结果的精度，首先进行网格无关性验证，并与实验数据[15]进行对比。雷诺数Re=1×106条件下原始DU96-W-180光滑翼型升、阻力系数Cl和Cd随攻角变化的计算结果如图6所示。从图6可以看出，当网格数量增加到168.8万以后，继续加密对升、阻力系数的计算结果影响极小，本文中等网格、密网格得到的计算结果、实验结果[15]以及XFOIL程序的计算结果[15]吻合较好。出于计算精度和资源的考虑，本文选用中等网格作为后续研究的基准网格。

(a) 升力系数

4°攻角下原始DU96-W-180光滑翼型表面压力系数分布的对比如图7所示。从图7可以看出，所计算的表面压力系数Cp分布与文献[15]的计算结果吻合，也验证了本文数值方法的可靠性。

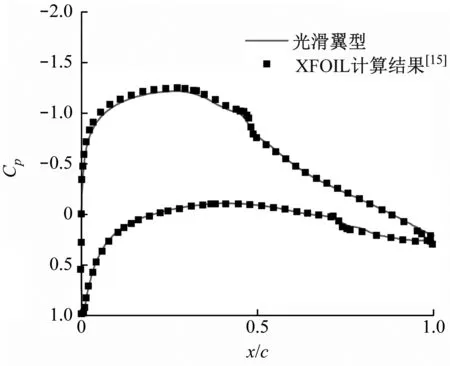
图7 表面压力系数分布结果对比

2 计算结果与分析

2.1 沟槽尺寸对表面沟槽减阻效应的影响

沟槽深度对风力机翼型气动性能有显著影响，此外，沟槽宽度和间隔也是需要考虑的因素。在雷诺数Re=1×106条件下，根据最佳减阻点h+=11估算出h约为0.000 25 m。对于DU96-W-180翼型，光滑翼型和表面布置沟槽的仿生翼型阻力系数对比如图8所示。

(a) L型沟槽

总体上，L型沟槽的减阻效果要优于V型沟槽。当s=0.000 25 m，w=0.000 50 m，h=0.000 25 m时，L型沟槽具有最佳减阻效果；在4°攻角下，该仿生翼型的升力系数提升1.67%，阻力系数降低5.60%，升阻比提升7.70%。对于V型沟槽，当s=0.000 4 m，h=0.000 25 m时，表面沟槽具有最佳减阻效果；在4°攻角下，升力系数提升1.60%，阻力系数降低3.70%，升阻比提升5.50%。

4°攻角下表面布置最优L型沟槽的仿生翼型与原始光滑翼型表面压力系数分布的对比如图9所示。可以看出，表面布置沟槽后，翼型的压力系数分布相比原始光滑翼型变化很小。在x方向和y方向上，光滑翼型和仿生翼型对应的Cp曲线围成的图形面积几乎相等，这也说明，仿生沟槽几乎不会提升翼型的升力，也几乎不会增加翼型的压差阻力。

(a)

光滑翼型和表面布置最优L型沟槽的仿生翼型展向平均后全流场的间歇因子分布如图10所示。从图10可以看出，仿生翼型表面流动转捩位置相比光滑翼型要略微靠后。布置沟槽后，吸力面转捩位置大约从x/c=0.472往后推移至x/c=0.485，压力面转捩位置大约从x/c=0.73往后推移至x/c=0.75。在翼型表面布置仿生沟槽可以极小地延迟边界层内的流动转捩，而流动转捩带来的摩擦阻力系数的减小是可以忽略的。

翼型的壁面摩擦力系数Cf反映了摩擦阻力的大小，表面布置最优L型沟槽的仿生翼型前缘处壁面摩擦力系数分布如图11所示。沟槽底部近乎为“死水”区，摩擦力系数很小，沟槽顶部的摩擦力系数远远大于底部。在沟槽的侧壁面，摩擦力系数从沟槽底部接近于零急剧增大到沟槽端口处的极大值。

(a) 光滑翼型

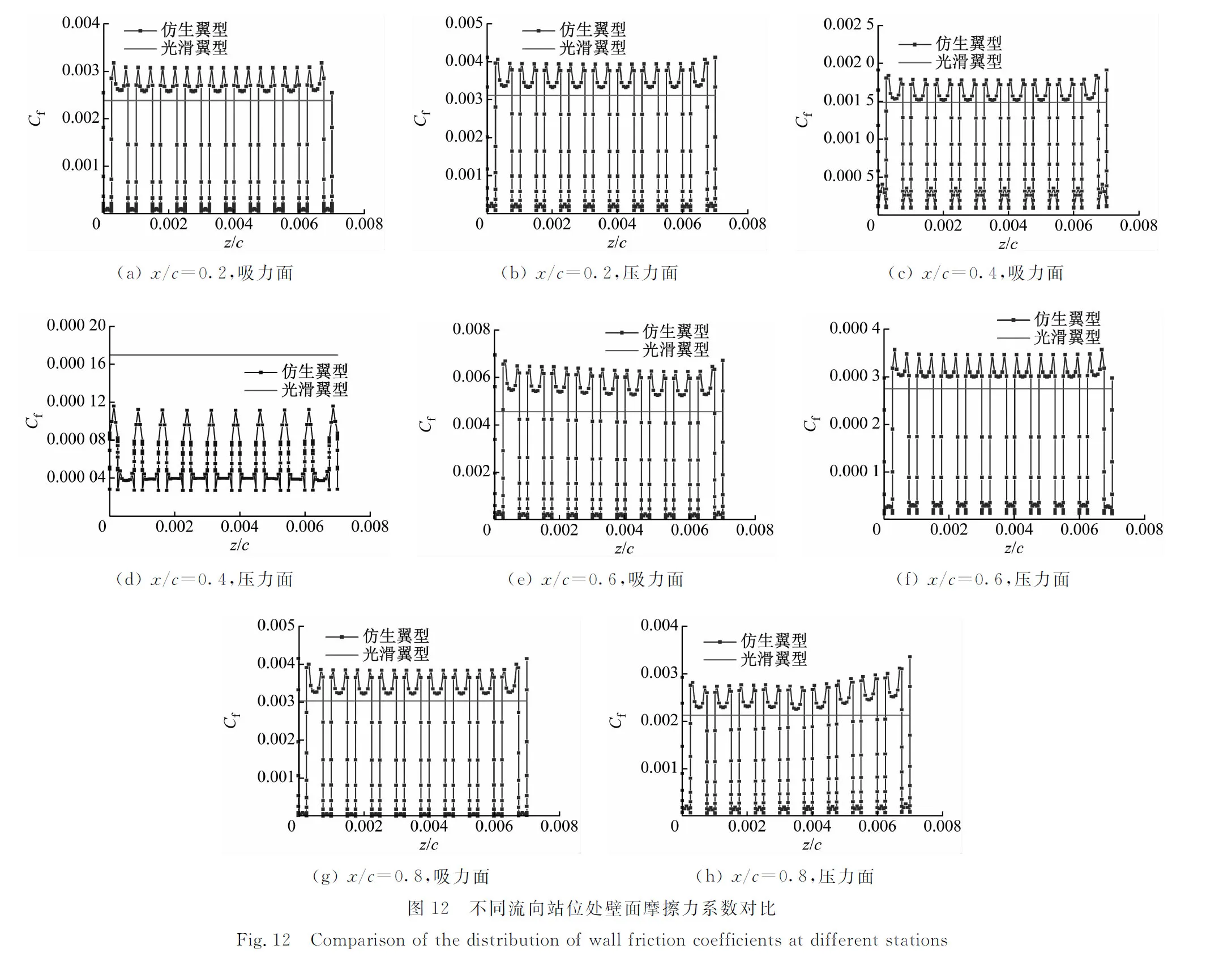
图12给出了4°攻角下光滑翼型和表面布置最优L型沟槽的仿生翼型壁面摩擦力系数沿翼型展向的对比，其中z为翼型展向坐标。在4个不同流向站位处(x/c=0.2、0.4、0.6和0.8)，仿生翼型的壁面摩擦力系数沿展向呈现规律变化，总体上仿生翼型壁面摩擦力系数峰值要略高于光滑翼型，但其壁面摩擦力系数展向均值要低于光滑翼型。在翼型压力面x/c=0.4处，壁面摩擦力系数有极小值，光滑翼型和仿生翼型两者的壁面摩擦力系数值都很小，但仿生翼型壁面摩擦力系数的峰值和展向均值都小于光滑翼型。布置表面沟槽后，两沟槽之间的翼型表面附近流速加快，摩擦力系数也随之增大，在沟槽端口处壁面摩擦力系数达到最大(峰值比光滑翼型高约30%)。同时，沟槽底部流体受壁面约束的影响，流速很小，相比顶部，沟槽底部壁面摩擦力系数要小一个量级。在这4个不同流向站位处(除了压力面x/c=0.4)，仿生翼型壁面摩擦力系数均值相比光滑翼型要低30%～40%。布置表面沟槽后，仿生翼型的壁面摩擦力系数总体上是降低了，表面沟槽对翼型的减阻效应取决于摩擦阻力的减小。

2.2 雷诺数对表面沟槽减阻效应的影响

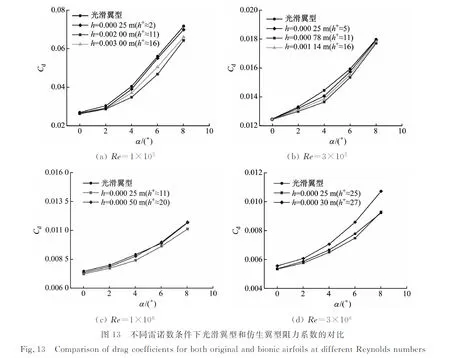
当雷诺数Re=1×105时，h=0.000 25 m对应的无量纲沟槽深度h+≈2，此时沟槽深度处于黏性区，4°攻角下表面沟槽减阻效果达到最佳，相比光滑翼型，仿生翼型的阻力系数降低了3.46%。沟槽深度h=0.002 m (h+≈11)处于最佳减阻点附近，此时4°攻角下翼型的阻力系数最大降幅达到14.06%。随着沟槽深度进一步增大，当h=0.003 m (h+≈16)时，沟槽的减阻效果有所降低，最大减阻率降为9.78%。

当雷诺数Re=3×105时，h=0.000 25 m对应的无量纲沟槽深度h+≈5，最大减阻率为2.70%。h=0.000 78 m (h+≈11)处于最佳减阻点附近，在该雷诺数下仿生翼型的阻力系数相比光滑翼型最大可降低5.54%。随着沟槽深度进一步增大，h=0.001 14 m (h+≈16)时，最大减阻率降为4.08%。与Re=1×105的低雷诺数工况相比，在该雷诺数条件下，整体上表面沟槽的减阻效果有所减弱。

当雷诺数Re=3×106时，因沟槽建模时存在困难无法实现最佳无量纲参数对应工况的模拟，故只能将h=0.000 25 m应用于模型中，所对应的无量纲h+≈25，在α=2°～6°依然有减阻效果，但升力系数均有所降低，最大减阻发生在6°攻角时，阻力系数可降低3.86%，升力系数降低1.86%。进行无量纲参数h+≈27的计算，发现全攻角的气动特性均恶化。上述算例说明在不同雷诺数下，h=0.000 25 m沟槽均具有优化翼型气动特性的效果。

2.3 表面沟槽对不同翼型气动性能的影响

为验证仿生沟槽对其他翼型也有气动优化效果，将h=0.000 25 m应用于厚度接近的S809翼型及NACA0018翼型，来流雷诺数Re=1×106。不同翼型对应的阻力系数如图14所示。

(a) S809翼型

对于S809仿生翼型，最大提升和减阻均发生在4°攻角时，升力系数提升约为3.7%，阻力系数可降低12.6%。对于NACA0018仿生翼型，最大提升和减阻也均发生在4°攻角时，升力系数提升约为1.0%，阻力系数可降低8.3%，表明这两款不同厚度的翼型对沟槽的敏感度要高于DU96-W-180翼型，有更明显的减阻效果。S809、NACA0018翼型表面布置最优L型沟槽的仿生翼型前缘处壁面摩擦力系数分布如图15和图16所示，可以看出二者的摩擦力系数峰值高于DU96-W-180翼型。沟槽底部近乎为“死水”区，摩擦力系数很小，沟槽顶部的摩擦力系数值远远大于底部。在沟槽的侧壁面，摩擦力系数从沟槽底部接近于零急剧增大到沟槽端口处的极大值。仿生翼型峰值处的摩擦力系数高于原始翼型，但考虑到底部的低摩擦力区，沿展向的壁面摩擦力系数均值要低于原始翼型。

(a) 光滑翼型

(a) 光滑翼型

3 结 论

(1) 在翼型表面布置微型沟槽可以有效降低阻力。当来流雷诺数Re=1×106，攻角为4°时，布置h=0.000 25 m的L型沟槽，对于DU96-W-180翼型可使阻力系数降低5.6%；同等条件下S809翼型可降低12.6%，NACA0018翼型可降低8.3%。

(2) 表面沟槽的减阻效果受来流雷诺数、沟槽尺寸、沟槽类型以及翼型的影响。随着来流雷诺数的增大，减阻效果有所降低。随着沟槽深度的增加，减阻率先增大后减小，最佳减阻点位于h+≈11。L型沟槽的减阻效果普遍优于V型沟槽；S809、NACA0018翼型对表面L型沟槽的敏感度高于DU96-W-180翼型。

(3) 在翼型表面布置微型沟槽可以略微延后转捩的发生，对3款翼型压差阻力和升力的影响几乎可以忽略。壁面摩擦力系数的减小是翼型减阻的主要原因，虽然仿生翼型在部分站位槽口处的摩擦力系数高于光滑翼型，但是在展向上仿生翼型从槽底到槽口的平均值都小于光滑翼型，因此总体摩擦力系数减小，阻力也随之减小。