板式扩散焊矩形微通道换热器中S-CO2 流动与传热特性的数值模拟

李 洪， 任 燕， 章立新， 高 明， 刘婧楠， 杨其国

(1.上海理工大学 能源与动力工程学院，上海 200093； 2.上海市动力工程多相流动与传热重点实验室，上海 200093)

发展新型高效发电技术是提高能源利用效率、实现节能环保最直接有效的方式[1]。相对于传统工质的动力循环系统，超临界二氧化碳(S-CO2)布雷顿循环系统具有效率高、洁净度高、灵敏度高、成本低以及结构紧凑等优点[2]，被认为是新兴能源利用方式中最具应用前景的能源转换系统之一，得到了国际学术界和工业界的广泛关注[3]。

目前，S-CO2布雷顿循环已成为第四代先进核能系统的备选热力方案之一[4]。循环系统中的热交换器(如预冷器、回热器等)是系统中的重要部件，直接影响着整个系统的高效性和紧凑性。印刷电路板式换热器(PCHE)自面世以来，由于性能优势，且契合我国能源技术转型升级和未来碳中和的需求[5]，在太阳能工程、液化天然气工程和核反应堆工程等领域得到了广泛的关注[6]。研究表明，使用条件、流体流态及通道结构等因素均会影响PCHE的流动与传热特性，且在确定的应用背景下，通道结构的影响最为显著。PCHE通道结构分为连续型和非连续型，涵盖直线型、折线型、S形和翼型等多种形式；通道截面包括圆形、半圆形、矩形、三角形和梯形等多种形状。受制于蚀刻加工技术，目前半圆形截面通道的研究应用较为广泛[7]。Geyer等[8]在恒定热流密度的边界条件下，对比分析了半圆形截面直线型通道与S形通道的传热效果，结果表明对于充分发展的层流流动而言，S形通道能够达到强化传热的目的，同等工况下的强化效果可达2.5～3倍。Gupta等[9]探索了恒定热流密度时通道截面形状对传热特性的影响，结果表明在雷诺数(Re)低于200时，不同截面形状的传热效果为三角形>矩形>半圆形>圆形。Lee等[10]对比了折线型通道不同截面形状对传热特性和压降特性的影响，证实矩形通道同时具有最佳的传热特性和最大的阻力损失。范凌灏等[11]的研究发现，在保持矩形微通道当量直径不变的情况下，随着截面高宽比的增大，通道表面的平均努塞尔数逐渐升高，传热性能得到提升，但压降也随之增大，流动恶化，微通道换热器的综合性能降低。Cui等[12]对翼型翅片通道的分析结果表明，将形状适宜的翅片交错排布可以使得近壁边界层周期性发展和消失，削弱边界层对流动传热的影响，实现强化传热。综上可知，优化通道的截面形状及扰流部件有助于实现强化传热、改善流动特性，但往往会造成生产工艺复杂、生产成本高昂等问题。因此，加工工艺便捷高效的矩形通道型PCHE在实现其流动与传热综合性能优化之后，将会拥有广阔的应用前景。

此外，S-CO2布雷顿循环系统中PCHE内的工质为超临界流体，超临界流体是当CO2的温度和压力均高于临界点(31 ℃和7.4 MPa)之后的一种状态，其基本物理性质(包括密度、黏度及扩散性等)均处于气体与液体之间，具有气液的双重特性：其黏度和扩散系数接近气体，因此具有良好的流动性能、渗透性能和传递性能[13]。

随着对PCHE研究的不断深入，以S-CO2为循环工质的实验和理论研究在流动范围、应用领域等方面仍然存在以下不足之处：通道内S-CO2流动与传热局限于低雷诺数范围，且冷侧和热侧通道内工质均为S-CO2的研究尚不充分等[14]。为此，笔者以S-CO2为循环工质，对板式扩散焊矩形微通道换热器内的流动与传热特性展开数值模拟，建立了适用的流动与传热数学物理模型，探索不同Re条件下扰流格栅对微通道内流动与传热特性的影响机理，从微通道的流动特性、传热特性及综合性能等角度进行分析，以提高微通道换热器的流动换热综合性能，并为换热器的结构优化提供理论依据。

1 板式扩散焊矩形微通道换热器的数学物理模型

1.1 物理模型及边界条件

传统PCHE的加工是通过在金属板片上进行光电化学刻蚀形成通道，其工艺复杂、成本高昂[15]。笔者选用的新型板式扩散焊矩形微通道换热器结构如图1所示。该换热器利用激光切割316L不锈钢金属板片，随后以扩散焊方式将9片金属板按照一定次序堆叠形成一组冷热通道，其中第1、第5、第9片为冷热流体换热界面，第2、第3、第4和第6、第7、第8片分别形成热流体通道和冷流体通道(以下分别简称为热通道和冷通道)，每3片金属板的厚度为矩形微通道的高度，而冷热通道中格栅分别位于第3和第7片，堆叠而成的逆流换热单元如图1(b)所示，经换热单元周期性重复排列，最终组成一个完整的换热器。

换热器包含18个换热单元，换热器外观尺寸长×宽×高为411.0 mm×112.0 mm×43.6 mm，其中矩形通道断面尺寸为3.00 mm×2.85 mm，格栅高度为0.95 mm。格栅高度是本文换热器结构中的最小几何尺寸(即板片的厚度)，本文数值模拟所使用的网格在壁面附近需设置细密的边界层，因此不宜直接选用完整的换热器或者换热单元作为数值模拟对象，以免影响数值模拟的效率和精度。为此，对换热单元的结构进行了简化，建立了如图1(c)所示的冷热通道单元的几何模型，其中矩形通道与格栅等的几何尺寸均为换热器的实际尺寸。

此外，建立了总长度和当量直径相同的半圆形直通道与矩形通道几何模型，如图2(a)所示，其中g为重力加速度。研究表明，在通道内增设扰流格栅，可以起到强化传热的效果[16]。因此，在图2(c)所示的矩形通道基础上，设置了如图2(d)～图2(g)所示的不同的扰流格栅，探索其对换热单元流动与传热特性的影响。图2(e)中的冷热通道几何模型即为图1(c)所示的冷热通道中部设置水平格栅的换热器几何模型。各个模型的相关几何尺寸见表1。

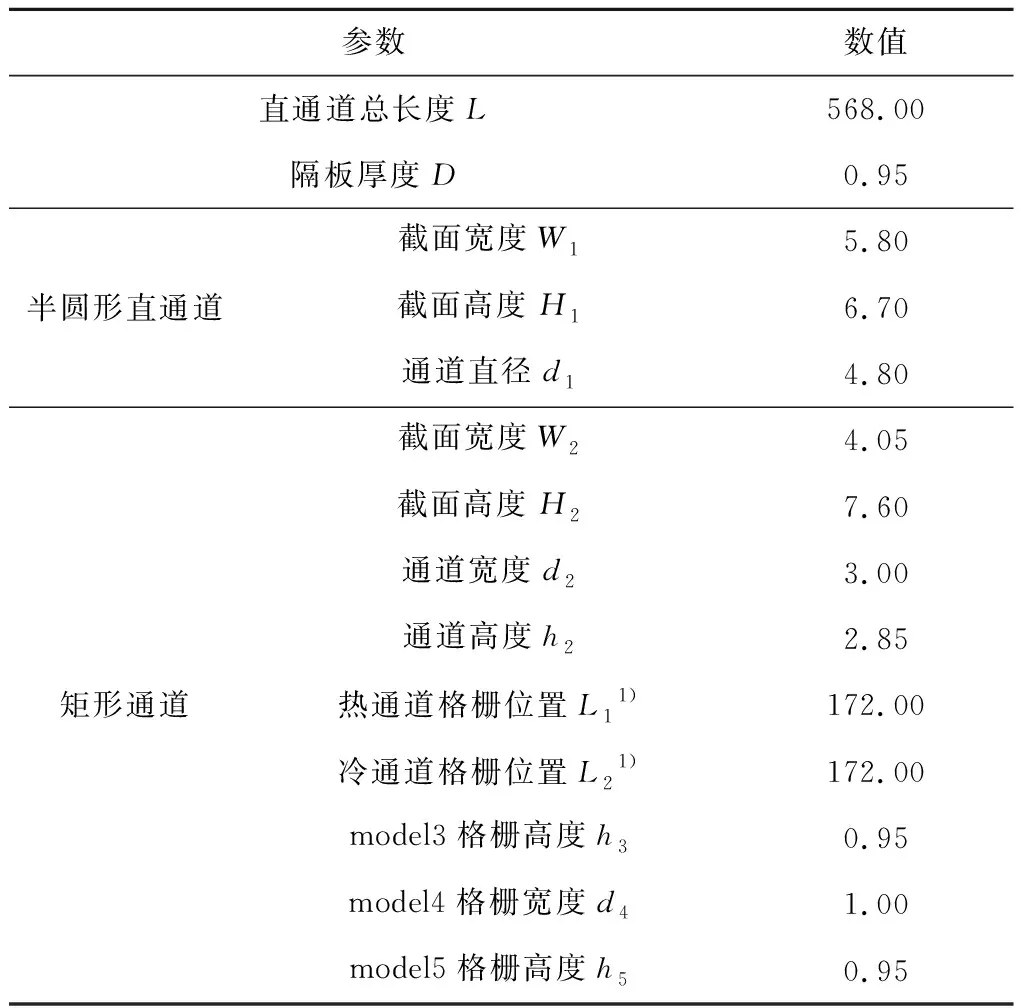
表1 冷热通道结构参数

利用Ansys Fluent 18.0软件展开数值模拟研究，其中S-CO2热物性参数来自于REFPROP V9.1，并通过引入实际气体模型(NIST Real Gas)实现动态求解。数值模拟边界条件见表2，其中计算域固体区域材料为316L不锈钢，其密度、比定压热容和导热系数分别为8 360 kg/m3、0.417 kJ/(kg·K)和0.021 kW/(m·K)。

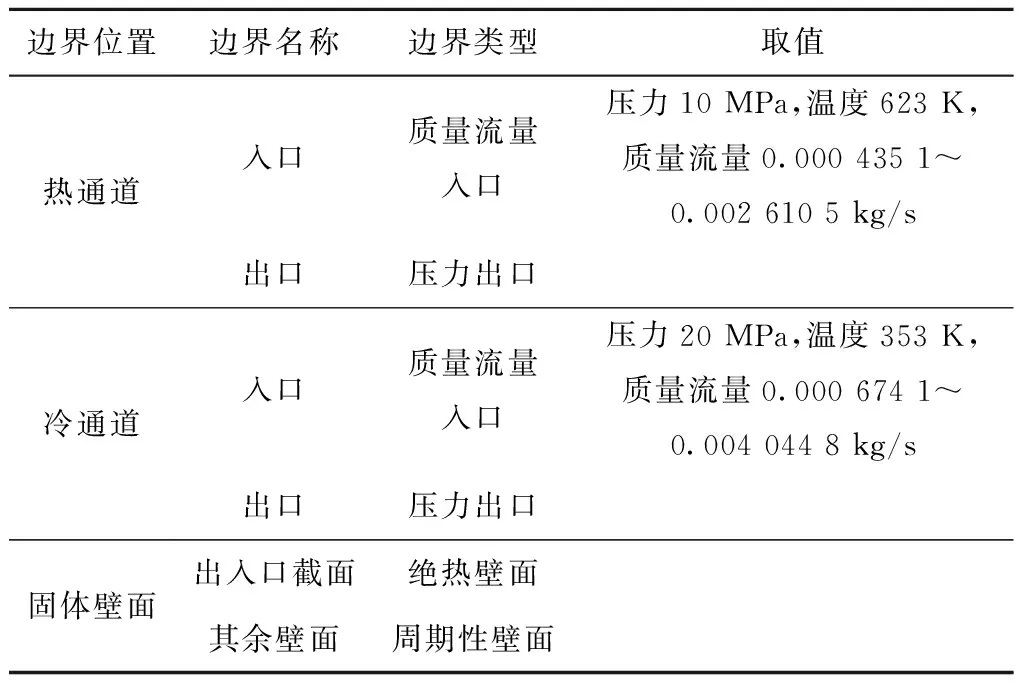
表2 数值模拟边界条件

1.2 流动与传热模型

板式扩散焊矩形微通道中S-CO2流动与传热特性研究的数值模拟控制方程[17]如下：

连续性方程

div(ρu)=0

(1)

动量方程

(2)

ρg+Sv

(3)

(4)

能量方程

(5)

式中：ρ和μ分别为流体的密度和动力黏度；p和T分别为压力和温度；K和c分别为流体传热系数和比热容；u、v和w分别为流体沿x、y和z方向的流速分量；S为广义源项；μt为湍动黏度，本文选用SSTk-ω湍流模型进行湍流计算，因此μt根据式(6)[18]计算。

μt=ρk/ω

(6)

式中：k和ω分别为湍动能和湍动频率，计算方法详见式(7)和式(8)。

Yk+Sk

(7)

Yω+Sω

(8)

式中：Gk为由层流流速梯度而产生的湍动能；Gω为由ω方程产生的湍动能；Γk和Γω分别为k和ω的有效扩散率；Yk和Yω分别为k和ω的发散项；Sk和Sω为自定义源项。

数值模拟选用稳态计算，求解方法采用基于压力-流速耦合的SIMPLE算法，压力项采用二阶迎风离散格式，梯度项采用格林-高斯离散格式，动量和能量均采用二阶迎风离散格式。

1.3 流动与传热特性评价指标

选取努塞尔数(Nu)和流动摩擦阻力系数(f)表征S-CO2在不同通道内的传热特性和流动阻力特性。Nu越大表明流体与壁面之间的传热系数越大；f越大表明流体在通道内的流动损失越大[19]。Nu和f的计算方法如下：

(9)

(10)

式中：qw为监测得到的冷热通道壁面热通量；De为通道的当量直径；λ为通道内流体的导热系数；Tf和Tw分别为流体和壁面的温度；Δp为通道进出口处流体之间的压差；uc为流体流速。

为了兼顾传热特性和流动特性，以综合传热增强因子(PEC)θ作为表征流动与传热特性的综合指标，计算方法见式(11)。当PEC大于1时，表示综合性能优于比较基准(以图2(c)所示的无格栅矩形通道为比较基准，其努塞尔数和流动摩擦阻力系数分别为Nu0和f0)。

(11)

2 模型验证

2.1 网格无关性验证

通过Ansys ICEM在几何模型计算域生成六面体结构化网格，网格质量在0.9以上。为准确反映通道内流体真实的流动与传热状态，在冷热通道壁面处设置了细密的边界层网格。边界层网格的初始高度为0.001 6 mm，增长率为1.2，以确保靠近壁面第一层网格节点处的y+小于1。

为验证网格无关性，选取65万、91万、126万和214万4种网格数展开数值模拟。其中，冷、热通道S-CO2的入口质量流量分别为2.022 4×10-3kg/s和1.305 2×10-3kg/s，其余参数见表2，数值模拟结果如图3所示。

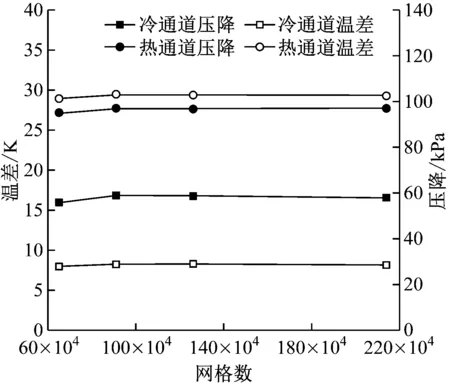
图3 不同网格数下冷热通道内的流动与传热特性

由图3可知，在相同的工况条件下，冷热通道中的压降和温差均随着网格数的增加而变化，并在网格数超过91万时基本趋于稳定，表明此时网格数增加对计算结果的影响可以忽略。因此，为提高计算效率，选用126万网格方案进行数值模拟。

2.2 模拟准确性验证

以Meshram等[20]的研究结果为参考标准，在相同的边界条件下验证所建物理模型的准确性，几何模型采用半圆形直通道模型(即model1)。验证结果见表3，其中误差为(模拟值-参考值)/参考值。

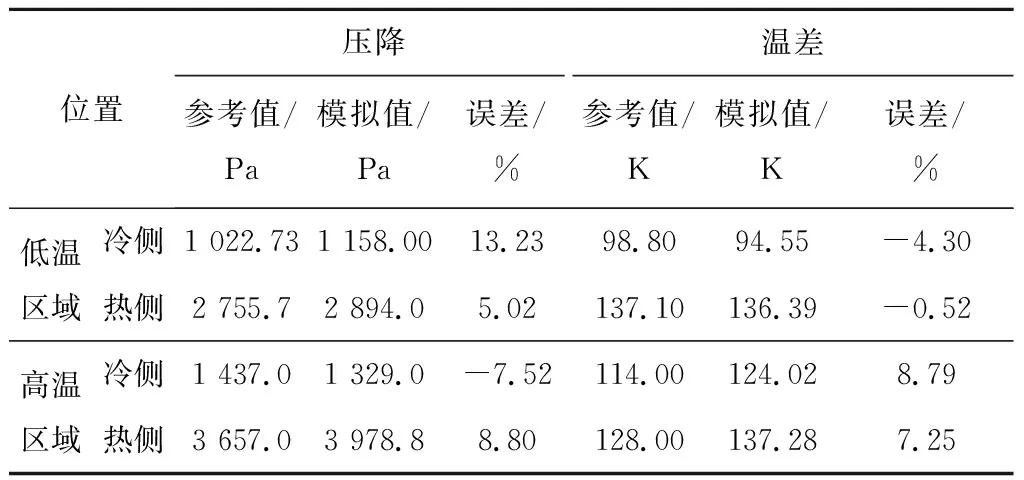
表3 模拟准确性验证结果

由表3可知，数值模拟得到的冷热通道内的压降及温差与参考值基本一致，压降的误差范围为-7.52%～13.23%，温差的误差范围为-4.30%～8.79%。综上所述，所建立的冷热通道换热单元数学物理模型可以满足S-CO2流动与传热特性数值模拟的准确性要求。

3 结果与分析

3.1 无格栅时直通道内S-CO2的流动与传热特性

首先研究了通道截面为半圆形(图2(b))和矩形(图2(c))时冷热通道换热单元中S-CO2的传热特性和流动阻力特性，Nu和f随Re的变化情况如图4所示。由图4可知，当5 000≤Re≤30 000时，随着Re的增大，无格栅的冷热通道内Nu增大，而f则减小。这是由于当Re增大时，通道内流速升高、湍流加剧，增强了S-CO2与壁面之间的对流换热，因而表现出更好的传热特性；同时，流速升高使得近壁面附近的层流边界层变薄，通道中流动摩擦阻力相应减小。对比相同Re工况下的数值模拟结果不难发现，截面为半圆形的直通道传热性能较弱但流动摩擦阻力较小，而截面为矩形的直通道传热性能较好，但流动摩擦阻力较大。

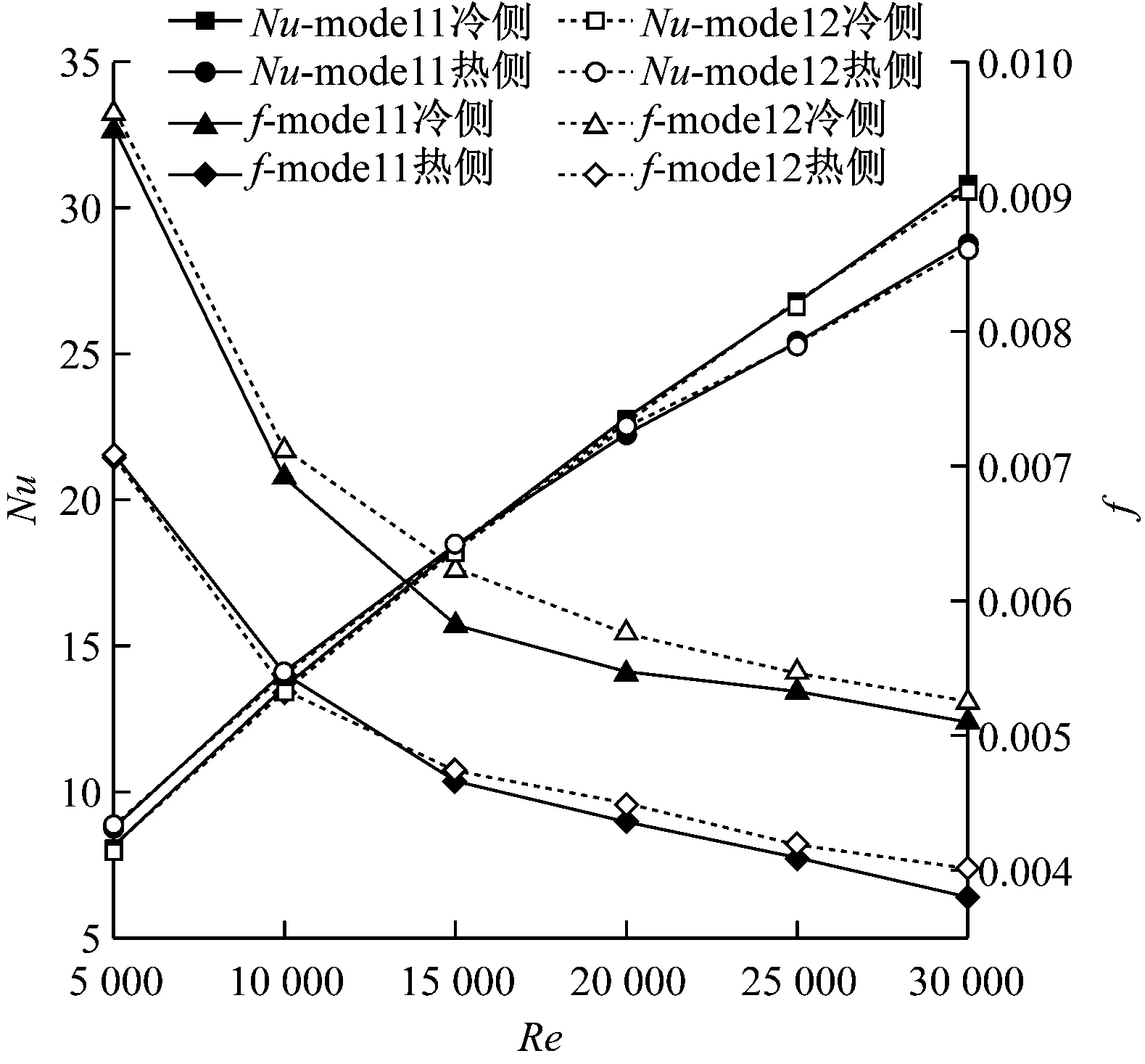
图4 无格栅时直通道内Nu和f随Re的变化情况

图5给出了无格栅半圆形直通道PEC随Re的变化情况。由图5可以看出，当Re>5 000时，在无格栅情况下，半圆形冷热直通道的PEC均略大于1，且在相同Re条件下，热通道内流速大于冷通道内流速，因而热通道的PEC均大于冷通道的PEC。此外，半圆形直通道内的PEC随着Re的增大先升高后降低，当Re为25 000左右时，综合传热效果最好。

图5 无格栅半圆形直通道PEC随Re的变化情况

综上所述，半圆形直通道的综合传热性能虽然优于矩形通道，但优势并不明显。因此，考虑到半圆形直通道加工工艺复杂、生产成本高昂，优化矩形通道结构、实现通道强化传热、提升综合传热性能更具实际意义。

3.2 设置格栅时矩形通道内S-CO2的流动与传热特性

为了分析通道内热流场情况，沿几何模型Z轴方向选取了4个取样面，取样面与热通道入口之间的距离分别为60 mm、175 mm、393 mm和508 mm，即第2个取样面位于热通道格栅下游3 mm处，第3个取样面位于冷通道格栅下游3 mm处。图6给出了Re为20 000时，3种扰流格栅设置方式对矩形通道内温度分布的影响。由图6可知，在相同Re条件下，热通道内的温度梯度大于冷通道内的温度梯度，且对比Z=175 mm和Z=393 mm处的温度云图不难发现，热通道内扰流格栅对温度场的影响更加显著。

图6 矩形通道内不同位置处的温度分布云图

Fig.6 Contours of temperature distribution at different positions in the rectangular channel

此外，由图2(b)可以看出，将扰流格栅设置在通道中部，对通道壁面处温度边界层的影响较小；而将扰流格栅设置在通道两侧，对通道壁面处温度边界层的影响则较大。将图6(a)与图6(d)、图6(e)对比可知，S-CO2经过位于通道两侧的水平格栅后，其对侧近壁处温度边界层变薄，近壁处流体与壁面之间的温度梯度减小，实现了热通道与冷通道之间的强化换热，其中图6(d)及图6(e)同为两侧水平格栅模型，不同的是图6(d)反映的是远离水平格栅换热界面处的温度分布，图6(e)反映的是紧靠水平格栅换热界面处的温度分布。考虑到湍动能是衡量流体混合能力的重要指标，冷热通道内S-CO2在流经扰流格栅后湍动能会发生急剧变化，以热通道为例，图7给出了通道中心截面处3种扰流格栅设置方式对热通道内S-CO2湍动能分布的影响。 以图7(a)为比较基准可知，图7(b)及图7(c)中在通道中设置扰流格栅可以显著增强流体扰动、促进流体混合，且图7(d)中扰流格栅下游流体的湍动能峰值最高、湍动程度最强、湍动范围最大。因此，将扰流格栅水平设置在通道两侧(即model5)时，扰流效果最好，可以有效改善近壁面流体与壁面之间的流动与传热。

图7 矩形热通道内S-CO2的湍动能分布云图

Fig.7 Contours of turbulent kinetic energy distribution of S-CO2 in the hot rectangular channel

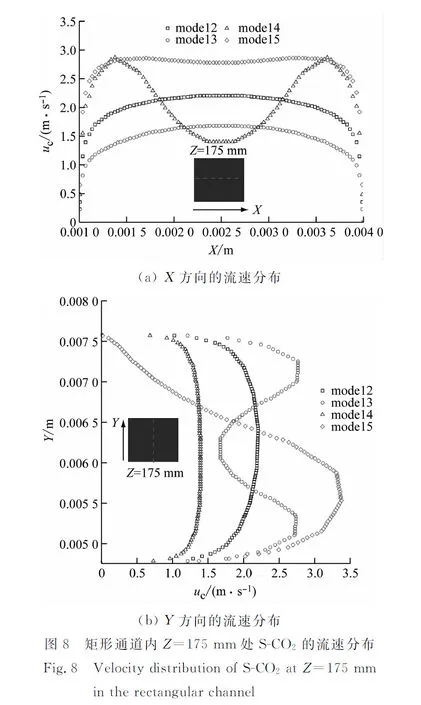
图8给出了Z=175 mm处矩形热通道内S-CO2的流速分布。由图8可知，无格栅时矩形通道(即model2)内S-CO2在X方向和Y方向的流速分布均呈梯形状，近似于管内完全发展的湍流流速分布；设置格栅后，随着格栅设置方式的变化，矩形通道内S-CO2在不同方向的流速分布呈不同V形驼峰状。在相同边界条件下，将扰流格栅水平设置在通道两侧(即model5)时，矩形通道内S-CO2在X方向的平均流速和Y方向的峰值流速分别为2.71 m/s和3.38 m/s，均为最大值，可以有效促进流体换热，但同时也会影响矩形通道内的阻力特性。

以无格栅矩形通道为比较基准，对比分析了不同格栅设置方式对通道内流动与传热特性的影响，如图9所示。由图9可知，在本文研究范围内，设置格栅后矩形通道内的Nu随着Re的增大而逐渐增大，而f则随着Re的增大而逐渐减小，且随着Re的持续增大，f的变化将趋于平缓，与图4中无格栅时矩形通道内Nu和f随Re的变化趋势相同。此外，随着Re的增大，矩形通道内的Nu/Nu0几乎保持不变，f/f0则缓慢增大。当Re相同时，将扰流格栅水平设置在通道两侧(即model5)，Nu/Nu0和f/f0相对较大，这意味着该通道的传热性能较好，但流动摩擦阻力较大；将扰流格栅水平或者竖直设置在通道中部(即model3或model4)，Nu/Nu0和f/f0差别不大，此时矩形通道的传热性能较差，但流动摩擦阻力也较小。

为了综合对比不同通道中的流动与传热特性，设置格栅后矩形通道内的PEC如图10所示。由图10可知，3种扰流格栅设置方式使得冷热通道内部的PEC均小于1，且随着Re的增大，PEC整体上呈缓慢下降趋势。与无格栅的矩形通道相比，设置格栅后虽然可以增强传热，但同时也会增大流动摩擦阻力，导致综合传热性能降低，且流速越高则综合传热性能越差。因此，矩形通道内扰流格栅的优化设计需在保障强化传热的基础上，尽可能降低对流动摩擦阻力的影响。对比图6～图10不难看出，在本文研究范围内，将扰流格栅水平设置在矩形通道两侧的扰流效果最好，在单独考虑传热特性时，其传热性能最优。因此，之后将在此基础上，进一步探索扰流格栅间隔、个数以及形状尺寸等因素对流动和传热特性的影响机理，实现通道综合传热性能以及换热器整体性能的优化。

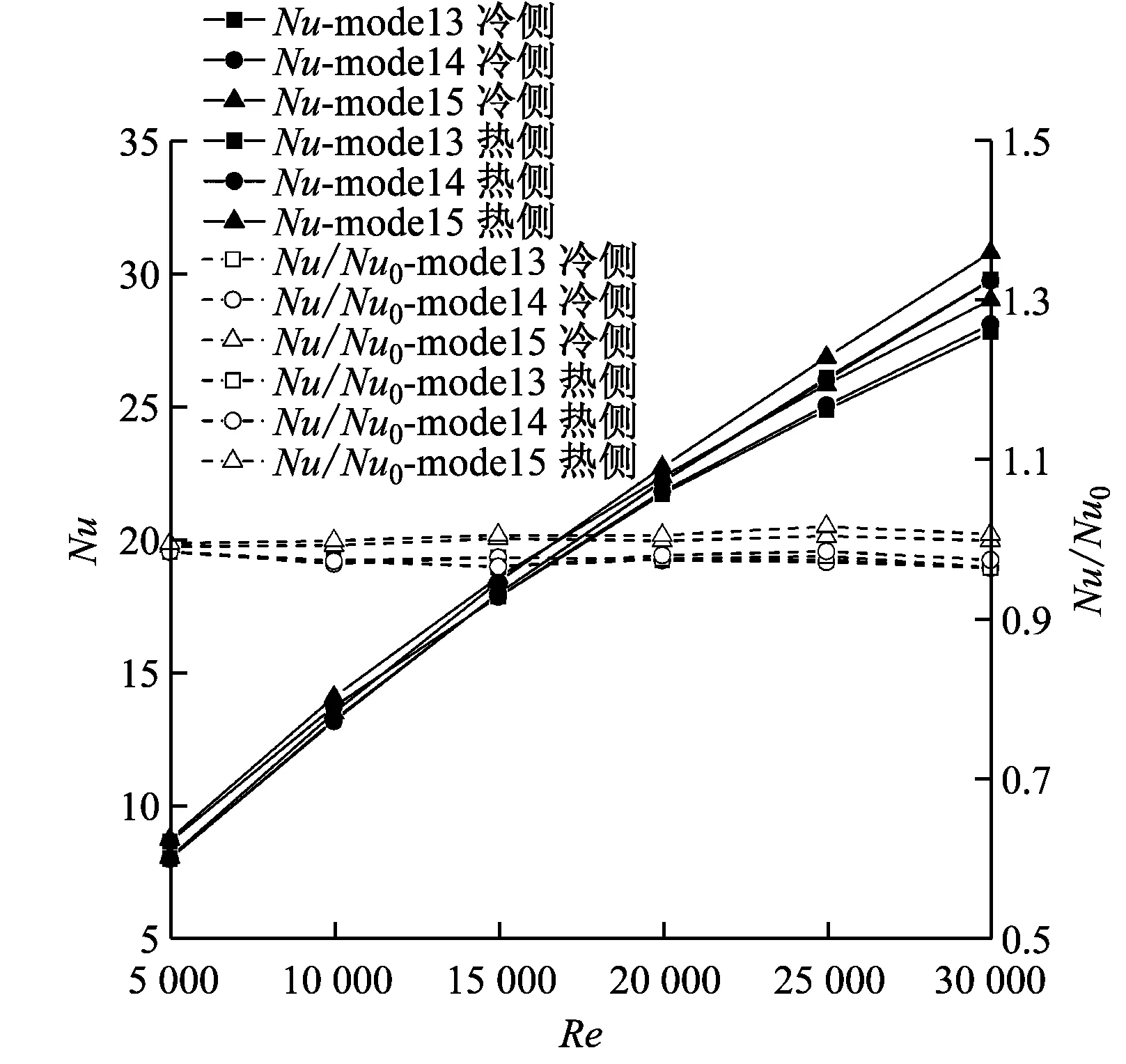
(a) Nu和Nu/Nu0随Re的变化情况

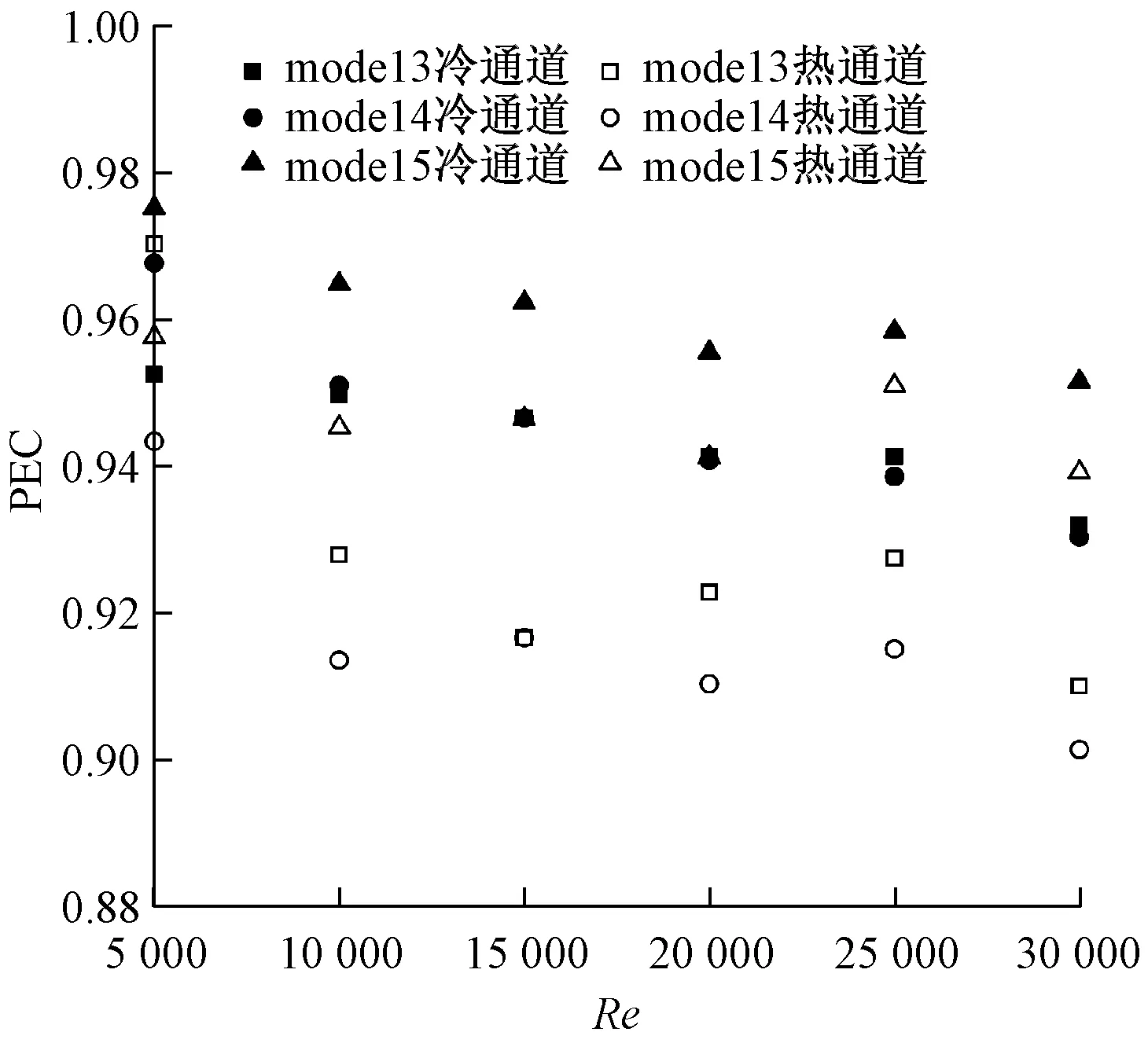
图10 设置格栅后矩形通道内PEC随Re的变化情况

4 结 论

(1) 随着Re的增大，板式扩散焊矩形微通道换热器换热单元冷热直通道内的S-CO2流速增大、湍流加剧，Nu随之增大，f反而减小。

(2) 未设置扰流格栅时，与矩形通道相比，在相同Re条件下，半圆形直通道的传热性能较弱，同时流动摩擦阻力较小，综合传热增强因子大于1，即相同当量直径的半圆形直通道的综合传热性能优于矩形通道。

(3) 设置扰流格栅后，在相同Re条件下，扰流格栅水平设置在矩形通道两侧时的扰流效果和传热性能最优，综合传热性能相对最高。

(4) 与半圆形直通道和无格栅矩形通道相比，目前的扰流格栅设置方式在增强传热的同时会增大流动摩擦阻力，导致综合传热增强因子降低。为兼顾换热器流动与传热特性以及生产制造成本，需以扰流格栅水平设置在通道两侧的换热单元为基础，进一步深入探索扰流格栅的优化设计。