考虑叶片旋转与土构耦合作用的海上风电机组 塔筒动态特性研究

樊 昂， 李录平， 欧阳敏南， 陈尚年

(长沙理工大学 能源与动力工程学院，长沙 410114)

目前，单桩式海上风电机组应用越来越广泛[1]。柔性风电机组由于较大的尺寸更容易受到外部振动源的影响，这可能会影响风电机组功率的输出，造成塔筒的疲劳损伤，甚至在极端条件下直接引发倒塔事故。为了保证海上风电机组的安全、可靠运行，准确了解风力机塔筒在外部振动载荷作用下的动态特性是非常重要的。对此，研究人员进行了大量的研究工作，以获得塔筒的动力学特性。

为了简化分析，通常假定风电机组处于停车状态，忽略叶片的几何构型以及塔筒与叶片之间的相互作用[2]，将叶片简化为位于塔顶的集中质量[3]或简化为两自由度系统。而在工程实际中，叶片的几何特性和转速直接影响作用在叶片上的风荷载[4]。此外,在运行条件下，叶片产生的离心力会改变叶片的刚度和模态频率[5],这反过来又会间接地影响塔筒的动态响应。因此，简化的集中质量模型与停机状况假设可能会导致结构响应估计不准确。而对于动力刚化效应的研究大多局限于叶片及风轮本身，并没有将其施加在塔筒动态特性分析中[6]。

另外，对于单桩这样一个细长的柔性基础，其与周围土体的相互作用是不可避免的，土构耦合(Soil-Structure Interaction，SSI)可以改变海上风电机组塔筒的振动特性和动力响应[7]，会降低塔筒的模态频率[8]。Bordón等[9]采用数值模拟和实验方法研究了土构耦合对风电机组振动特性的影响。然而在这些研究中，要么假设风电机组处于停车状态，风轮质量集中在塔筒顶部[10]，要么只注重于单桩基础性能的分析[11-12]，而对单桩上方的塔筒振动特性研究则相对较少。在实际工程中，海上风电机组的塔筒结构也很容易遭受破坏作用[13]，因此有必要研究塔筒在土构耦合作用下的振动特性。

笔者采用有限元软件Ansys对NREL 5 MW单桩式海上风电机组进行整体建模，模拟分析塔筒在叶片旋转与土构耦合共同作用下的动力响应。在建立叶片与土体三维实体模型的基础上，将叶片旋转时产生的离心力与离心刚度作为初始状态；在单桩周围建立分层土体模型，模拟土壤与塔筒单桩的相互作用，定量研究叶片旋转工况与土构耦合作用对塔筒动力学行为的影响。

1 风电机组有限元模型

1.1 NREL 5 MW单桩式海上风电机组模型

NREL 5 MW单桩式海上风电机组整体结构模型如图1所示，风电机组主要参数[14]如表1所示。

图1 NREL 5 MW单桩式海上风电机组三维实体模型

表1 NREL 5 MW单桩式海上风电机组主要参数

该风电机组的叶片采用聚酯材料，塔和单桩材料为钢。笔者不考虑海水振动引起的附加质量。风电机组结构材料属性见表2。

表2 风电机组结构材料属性

1.2 叶片旋转工况的施加

考虑到叶片旋转对塔筒振动特性的影响，将风电机组额定转速(12.1 r/min)工况下叶片旋转产生的离心力作为预应力形成离心刚度矩阵，然后将其叠加到模态和瞬态刚度矩阵上，以此来考虑叶片旋转产生的动力刚化效应。动力刚化效应下叶片的应力-应变关系[15]为：

σ=σr+Hε

(1)

式中：σ为叶片应力，MPa；σr为初始应力，MPa；H为应力-应变关系方程；ε为叶片应变张量。

叶片在旋转过程中产生的离心力总和Nr(i)为：

(2)

式中：r为叶片i点到转轴中心的距离，m；m(r)为单位长度质量，kg/m；Ωr为叶片旋转速度，r/min；Δr为单位长度;R为叶轮半径,m。

由叶片旋转引起的离心刚度矩阵K*为：

(3)

式中：Li为i单元长度，m；Ni为i单元离心力，N。

1.3 土-结构耦合作用模型

选择风电机组单桩土体模型的直径为80 m，高60 m，模型上下共分为3层：上层厚度为15 m，土质为淤泥质粉质黏土；中层厚度为15 m，土质为粉砂；底层厚度为30 m，土质为粉质黏土。土质参数采用江苏某海上风电场实测参数[16]，见表3。

表3 海上风电场土质实测参数

桩土接触底部采用硬接触形式，侧向采用摩尔库伦摩擦罚函数形式，通过摩擦因数定义接触面关系，表达式为：

τc=μp

(4)

式中：τc为接触面滑移临界切应力，MPa；μ为摩擦因数；p为接触压力，MPa。

土体边界条件为：底边三向固定约束，外侧径向位移约束。模型中将单桩内部填充物视为混凝土。单桩土体模型内部截面示意图如图2所示。

图2 单桩土体模型内部截面示意图

为减小计算误差，在进行动态分析之前对单桩土体模型进行初始应力平衡。先向单桩土体模型施加重力载荷，再将得到的土体内部应力作为初始条件写入模型。

1.4 单桩式海上风电机组结构运动数学模型

单桩式海上风电机组结构运动微分方程[17]为：

(5)

附加水质量和离心刚度矩阵后，风电机组结构运动微分方程变为：

(6)

式中：M0为考虑附加水质量的结构质量矩阵；K0为结构整体刚度矩阵。

M0可以表示为：

M0=M+M*

(7)

式中：M*为附加质量矩阵。

C采用Rayleigh阻尼：

C=αM+βK

(8)

(9)

式中：ωi、ωj分别为第i阶和第j阶振型的模态频率，Hz；ξi、ξj分别为第i阶和第j阶振型阻尼比。

结构整体刚度矩阵K0为：

K0=K+K*

(10)

(11)

式中：L为线性应变-位移关系矩阵；ψ为振动幅值矩阵。

1.5 网格划分

采用Ansys Workbench自带网格划分模块进行网格划分，模型单元类型为实体单元，选择占用计算资源较少的四面体网格与质量较高的六面体网格相结合，在单桩与土体接触处细化网格[18]。由于单桩土体模型结构简单、尺寸较大，且笔者着重分析塔筒性能，因此设置单桩土体模型网格尺寸大于风电机组结构网格尺寸。同时进行网格划分无关性验证，以叶片旋转与土构耦合共同作用下塔筒瞬态响应前后方向位移最大值为算例，无关性验证结果如表4所示。

表4 网格划分无关性验证结果

由表4可知，方案三计算量合理，网格质量满足要求，算例结果与方案四差别不大，为合理利用计算资源，保证计算效率，故选择方案三作为本文网格划分方案。

2 风力机结构与载荷计算模型

2.1 脉动风载荷

湍流风的风速时程由平均风速和脉动风速组成，选取风电机组的额定风速(11.4 m/s)作为平均风速，脉动风功率谱选取IEC 61400-3标准[19]中的Kaimal模型，风速谱Sk(f)的表达式为：

(12)

(13)

式中：f为风速频率，Hz；σk为风速均方根值，m/s；Lk为整体尺度参数；uhub为轮毂高度处平均风速，m/s；Lu为湍流尺度参数，Lu=0.7min(60，hub)，其中hub为轮毂高度，m;k取a、b、c3个方向。

平均风速为11.4 m/s时100 s内的脉动风速分布如图3所示。

图3 平均风速为11.4 m/s时100 s内的脉动风速分布

作用在风电机组上的风载荷值按式(14)～式(19)确定。

作用在塔筒的风载荷Fz[20]为：

(14)

式中：ρ为空气密度，kg/m3；At为塔筒受风面积，m2；V为风速，m/s；Ce为阻力系数。

风剪切采用指数模型：

(15)

式中：Vh为距地面高度h处风速，m/s；α为切变系数。

风轮水平轴向推力Ft为：

(16)

式中：Ab为掠叶面积，m2；Ct为推力系数。

叶片气动载荷切向力Fy为：

(17)

式中：CP为风电机组风能利用系数；A为叶片切向面积,m2。

叶轮旋转力矩Mr为：

Mr=9 950Pγ/ω

(18)

式中：P为风电机组功率，W；γ为发电效率；ω为叶片转速，r/min。

叶轮俯仰力矩Mp为：

(19)

式中：B为叶片数；V1、V2分别为叶轮中心上、下2/3叶片长度处风速，m/s。

图4为塔筒顶部脉动风载荷100 s时程曲线。

图4 塔筒顶部脉动风载荷100 s时程曲线

2.2 海浪载荷

海浪会对单桩产生显著的水平方向作用力，且海浪的高度是不规则的，可以从各个方向影响风电机组结构。采用线性波浪理论描述海浪运动[21]：

(20)

式中：φ为速度势；Hw为海浪高度，m；ζ为波数；T为波浪周期，s；x为水平坐标；z为竖向坐标；d为水深，m；ωw为波浪圆频率，rad/s。

海浪高程η为：

(21)

(22)

(23)

采用Morison方程[22]计算海浪载荷Fwave：

Fwave=Fm+Fd

(24)

(25)

(26)

式中：Fm为惯性力，kN；Fd为拖曳力，kN；Cm为惯性力系数；ρw为水密度，kg/m3；D为结构直径，m；Cd为拖曳力系数。

单桩式海上风电机组是典型的高耸柔性结构，其自身的变形与位移不可忽略，海浪中水质点会受到影响，其速度和加速度会发生改变，因此要对式(25)和式(26)进行修正：

(27)

(28)

海浪载荷100 s时程曲线如图5。

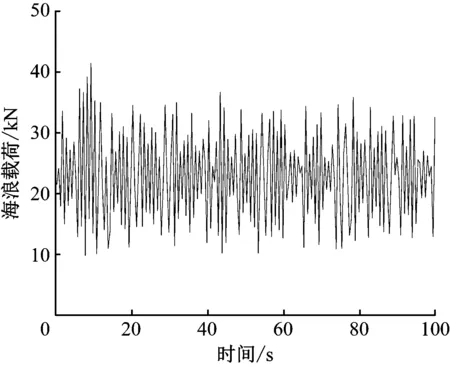
图5 海浪载荷100 s时程曲线

下面的模拟计算中，在2个计算工况下均施加了海浪载荷，施加位置在单桩高于海床之上的部分。

3 塔筒振动特性分析

3.1 不考虑土构耦合时塔筒振动特性分析

不考虑土构耦合时，风电机组模型不包含单桩土体模型，塔筒底部与单桩顶部绑定接触，单桩底部固定约束。将风电机组受载运行状况下的叶片应力矩阵与刚度矩阵施加在模型上，以此作为初始状态。

3.1.1 风电机组结构的模态特性

通过有限元计算，得到风电机组塔筒结构前六阶模态振型和模态频率，分别见图6和表5。由表5可知，叶片旋转时所产生的离心力和离心刚度会增大塔筒的模态频率，其中对前两阶模态影响最大，模态频率变化率分别为7.52%和7.10%。

表5 叶片旋转工况下塔筒结构模态频率

3.1.2 风电机组结构的位移响应特性

通过模拟得到的风电机组结构瞬态响应位移云图如图7所示。风电机组塔筒顶部前后方向与侧向位移时程曲线如图8所示。

由图7可知，沿塔筒高度的瞬态响应位移不同，最大位移响应出现在塔顶，因此仅讨论塔筒顶部位移。由图8可知，在叶片旋转工况下，塔筒顶部前后方向的位移主要在250～700 mm范围内波动，最大位移为846 mm。

(a) 机组总位移

(a) 前后方向

塔筒顶部侧向位移主要在75～250 mm范围内波动，最大位移为288.78 mm；侧向位移波动幅度较小，远不如前后方向位移波动幅度大。

计算结果表明，塔筒的侧向位移响应明显小于前后方向位移响应，出现这种现象的主要原因为：第一是数值模拟中，脉动风载荷只沿前后方向作用在塔筒上；第二是因为当叶片处于旋转状态时，叶片挥舞方向(对应于塔筒前后方向)上的风载荷远大于摆振方向(对应于塔筒侧向)上的风载荷，叶片上较大的风载荷导致塔架与叶片之间更剧烈的相互作用。

图9给出了叶片旋转工况下塔筒顶部前后方向与侧向加速度响应的功率谱密度。

(a) 前后方向

由图9可知，在0.247 6 Hz处出现明显峰值，这对应了结构一阶模态频率，说明主要能量集中在前两阶模态中。从图9可以很明显地看出能量在侧向上小得多，这导致在该方向上较小的塔筒位移响应。

3.1.3 风电机组结构应力分布特性

通过模拟得到的风电机组结构瞬态响应等效应力云图和最大等效应力时程曲线如图10所示。

(a) 等效应力云图

在此工况下，塔筒瞬态响应最大等效应力分布在塔筒与机舱连接处以及塔筒底部，最大等效应力出现在1.6 s，其值为703.65 MPa。

3.2 土构耦合作用下塔筒振动特性分析

3.2.1 风电机组结构的模态特性

通过有限元计算，得到叶片旋转与土构耦合共同作用下风电机组前六阶模态振型和模态频率，分别见图11和表6。

由表6可知，土构耦合作用会显著降低风电机组塔筒结构前两阶模态频率，前两阶模态频率的相对变化量分别为-31.68%和-31.74%。土构耦合对塔筒结构三阶、四阶模态频率的影响略小，其相对变化量分别为-4.75%和-4.41%。这是因为当考虑土构耦合时，单桩插入海床并被土壤包围，这使得塔筒比底部完全固定的情况下更灵活，土壤的弹性使整个结构系统的刚度降低，同时又增加了塔筒的参振质量，因此塔筒的模态频率降低。

表6 考虑土构耦合时风电机组塔筒结构模态频率

3.2.2 风电机组结构的位移响应特性

通过模拟得到的叶片旋转与土构耦合共同作用下风电机组结构瞬态响应位移云图如图12所示，塔筒顶部前后方向与侧向位移时程曲线如图13所示。

由图12和图13可知，在叶片旋转与土构耦合共同作用下，塔筒前后方向位移瞬态响应量明显增大，响应幅值在800～1 500 mm内波动；在41.5 s时，塔筒顶部前后方向最大位移为1 581.52 mm，与不考虑土构耦合时的最大位移846 mm相比，增幅为86.94%。这是因为考虑土构耦合后，土体结构的刚度、阻尼以及单桩周围土体的变形将会对风电机组结构的响应产生较大影响，使其位移和应力大大超过刚性基础下的结果，并且塔筒是高柔结构，该现象更为明显。

(a) 前后方向

与不考虑土构耦合时相比，考虑土构耦合后塔筒顶部侧向位移也有所增大,其响应幅值在175～375 mm内波动；塔筒顶部侧向最大位移出现在37.5 s，达到423.33 mm，与不考虑土构耦合时的最大位移288.78 mm相比，增幅为46.59%。塔筒顶部侧向位移波动幅度远小于其前后方向位移波动幅度。

图14给出了叶片旋转与土构耦合共同作用下塔筒顶部前后方向与侧向加速度功率谱密度。在0.157 Hz处塔筒顶部前后方向与侧向加速度功率谱密度出现明显的峰值，这对应了土构耦合作用下结构一阶模态频率。将图14与图9进行比较发现，考虑土构耦合时塔筒顶部加速度功率谱密度明显增大。

(a) 前后方向

3.2.3 风电机组结构应力分布特性

通过模拟计算，得到风电机组结构在叶片旋转与土构耦合共同作用下瞬态响应等效应力云图和最大等效应力时程曲线，如图15所示。由图15(b)可知，考虑土构耦合时塔筒瞬态响应最大等效应力出现在1.6 s，其值为1 107.4 MPa，相比于不考虑土构耦合时的最大等效应力703.65 MPa，增幅为57.38%。这是因为土体结构阻尼较小，对风电机组结构应力响应影响较大，且单桩周围的土体结构在挤压下产生位移，导致上部风电机组结构产生应力重分布。同时最大应力分布位置主要出现在塔筒底部和单桩处，与实际情况相符合。

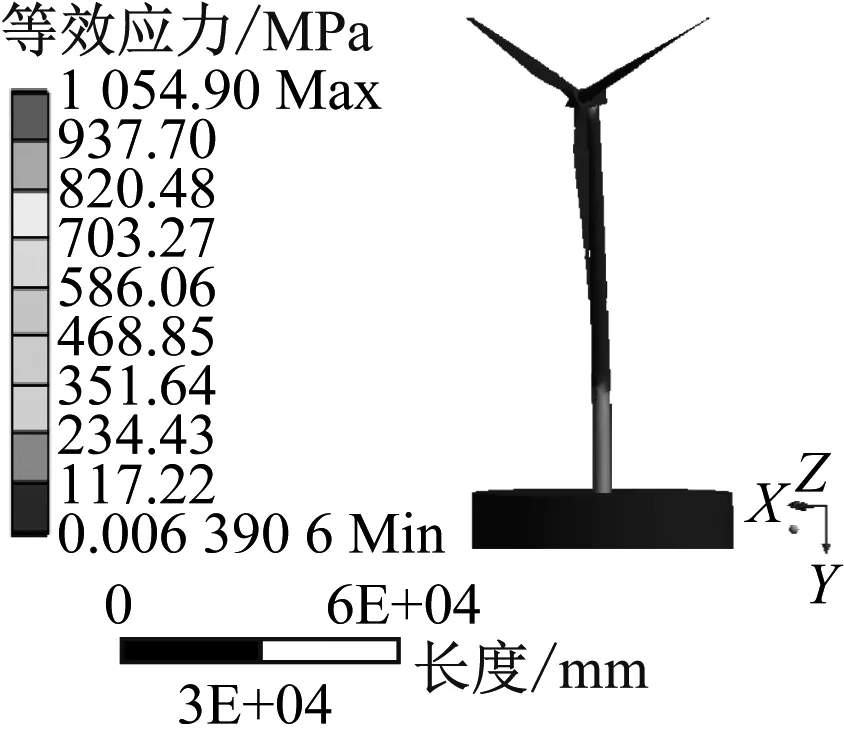
(a) 等效应力云图

3.3 风电机组结构共振分析

为了避免风电机组结构在复杂的外部激励作用下产生共振，利用坎贝尔图来甄别风电机组结构潜在的共振点，并通过风电机组结构的模态频率与叶片激励频率的重合点来识别。其中，风电机组单叶片旋转一周的激励频率称为1P，三叶片旋转一周的激励频率称为3P。当风电机组运行时，坎贝尔图中线条产生的任何交点即为共振点。

图16(a)为只考虑叶片旋转作用时的风电机组坎贝尔图，图16(b)为考虑叶片旋转和土构耦合共同作用时的风电机组坎贝尔图。

(a) 叶片旋转作用

由图16(a)可知，在考虑叶片动力刚化效应下，叶片以不同转速旋转时，在1P转频范围内，塔筒的一阶及二阶模态频率会在转速14.8 r/min附近与1P转频产生交点，发生共振。而三阶及四阶模态频率分别在转速14.5 r/min附近和15.8 r/min附近与3P转频产生交点，说明风电机组结构在该3P转频内存在2个共振点，15 r/min附近是风电机组易共振区域。风电机组以额定转速(12.1 r/min)运行时，在1P、3P转频激励下不会产生共振。

由图16(b)可知，在叶片旋转与土构耦合共同作用下，塔筒的一阶及二阶模态频率会在转速9.5 r/min附近与1P转频产生交点，发生共振，该点位于在风电机组达到额定转速之前，因此应在运行到此转速处快速通过，避免共振。而三阶及四阶模态频率分别在转速14 r/min附近和14.8 r/min附近与3P转频产生交点，该点与图16(a)差别不大，都位于额定转速外。

4 结 论

(1) 考虑土构耦合时，风电机组塔筒结构的前两阶模态频率显著降低，相对变化率分别为-31.68%和-31.74%,而对三阶～六阶模态频率的影响较小。

(2) 当风电机组以额定转速(12.1 r/min)旋转时，在叶片旋转与土构耦合共同作用下，塔筒顶部在前后方向和侧向上的最大位移比底部固定约束时大86.94%和46.59%。若忽略塔筒底部的土构耦合作用，可能导致非保守的结构响应估计和结构部件的不安全设计。

(3) 在叶片旋转与土构耦合共同作用下，塔筒的一阶及二阶模态频率会在转速9.5 r/min附近与1P转频产生共振点，在额定转速以内不会与3P转频产生共振。

(4) 在叶片旋转与土构耦合共同作用下，塔筒等效应力显著增大，最大等效应力相对于不考虑土构耦合时增大了57.38%，主要分布位置为塔筒底部和单桩处。