超临界压力下二氧化碳在水平管内传热异常特性研究

宿诗雨， 姜文全， 李 琳， 石杰峰， 李 洋， 杨 帆

(1． 辽宁石油化工大学 石油天然气工程学院， 辽宁抚顺 113001；2． 辽宁石油化工大学 机械工程学院， 辽宁抚顺 113001)

CO2因具有无毒、稳定性强、对环境影响小等特点，近年来在能源发电、核反应堆、航空航天、热泵与制冷等领域有较好的应用前景[1-2]。与传统蒸汽朗肯循环相比，超临界压力下的CO2循环系统具有热功转换效率高、灵活性强和经济性好的优势，近年来得到了广泛的商业应用，也为换热装置的设计及系统安全运行提供了理论基础[3]。超临界压力下的CO2在压力p=8 MPa时的热物性如图1所示。由图1可知，其热物性在温度T=307.8 K附近发生剧烈变化，尤其是比热容，在此温度点达到极大值，将此点称为拟临界温度点Tpc。

图1 p=8 MPa时的CO2热物性

超临界压力下CO2的传热可分为正常传热、传热强化和传热恶化3种模式。一般来说，将传热系数出现峰值的情况视为传热强化，将壁温飞升现象视为传热恶化[4-6]。在已有文献中，超临界压力下CO2大多数是在竖直管中开展实验与模拟研究的。在竖直流动中，流场对称，管壁的传热能力相同，但受浮升力效应影响，向上流动和向下流动不同。一般来说，在加热条件下，向下流动的传热能力比向上流动强[7-9]。

超临界压力下CO2在水平管中的流动相比在竖直管中的流动更加复杂。在水平流动中，因重力产生的浮升力发生在流动的垂直方向上，导致水平管上下壁传热特性出现差异。众多学者对水平管壁传热特性不同的解释也不尽相同：Adebiyi等[10]通过实验发现水平管顶部与底部传热能力不同，并发现底部传热效果较好；Liao等[11]通过实验发现当雷诺数(Re)高达105时，浮升力在水平流动中仍起重要作用；相梦如等[12]通过场协同原理解释了上下壁面换热不均匀的原因；闫晨帅等[13]着重研究水平管上壁的传热特性，发现在质量流量较低时，周向上壁较低的密度及湍动能与轴向较小的速度共同导致上壁出现高温现象；Kim等[14]通过实验发现，现有的浮升力判别因子临界值不适用于低热流密度工况，所以需要新的浮升力因子对水平流动作进一步评价。综上可得，浮升力与物性是造成水平管管壁传热特性不同的主要因素，且还需对水平管内浮升力的判定标准开展深入的研究。

笔者对超临界压力下CO2在4 mm水平管内传热过程进行数值模拟，分析了热流密度、压力和浮升力对传热的影响，通过对比确定了更适合本文工况下的浮升力标准，并根据截面的物性分布获得了水平管壁不同位置的传热特性。

1 物理模型与数值模拟方法

1.1 物理模型

三维物理模型如图2所示。水平管直径(d)为4 mm，管长(L)为1 000 mm，计算时忽略壁厚。水平管周向角度等于0°时定义为上母线(top)，周向角度为180°时定义为下母线(bottom)。

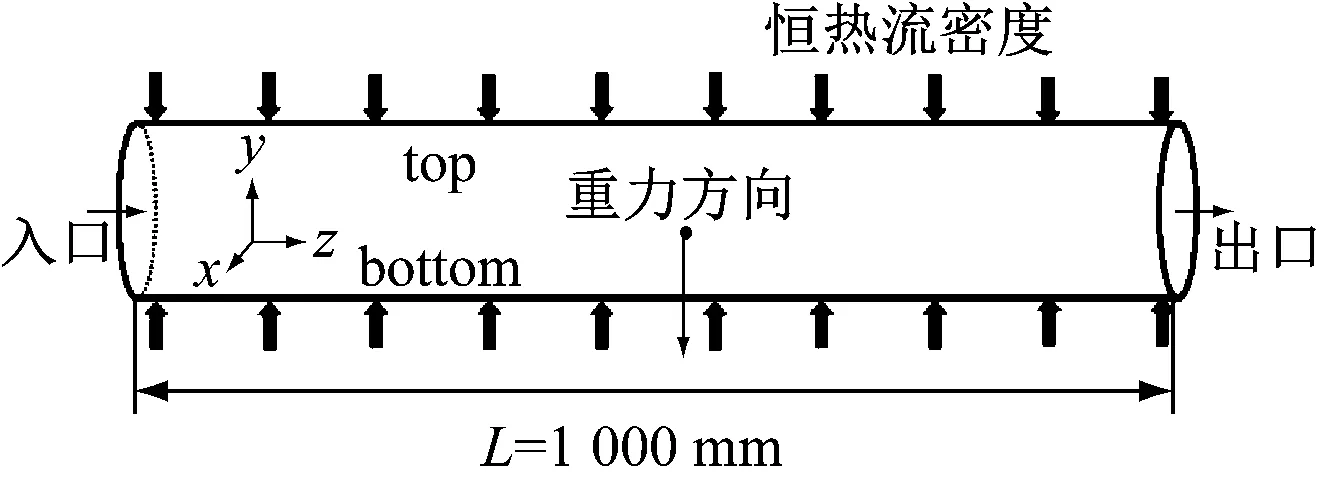
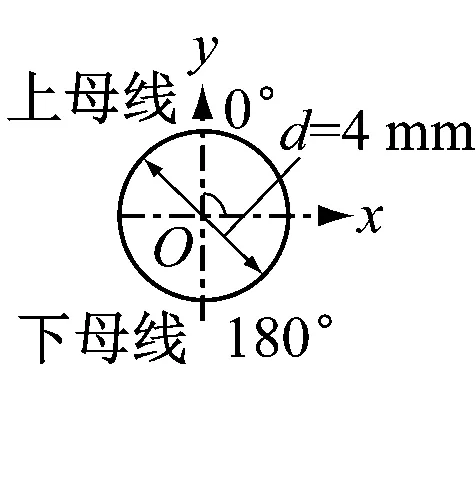
图2 水平管物理模型

1.2 网格划分与数值方法

计算区域内利用ICEM软件划分网格，圆形截面采用O型剖分保证网格质量，近壁面处网格进行加密处理，且第1层网格无量纲高度y+<1，如图3所示。采用FLUENT软件进行数值模拟，其中定压力和定温度下的物性参数通过REFPROP软件计算得到，并以线性插值方法输入。

图3 网格划分截面

边界条件如下：入口质量流量G为140～260 kg/(m2·s)；出口压力p为8 MPa；加热壁面恒热流密度(即壁面热流密度)qw为20～40 kW/m2；入口温度为 302 K。采用Standardk-ε增强壁面函数湍流模型，压力与速度耦合采用SIMPLEC算法，当连续性方程的残差小于10-5时，认为计算收敛。采用的数值模型中包括连续性方程、动量方程和能量方程，在三维直角坐标系下分别用以下方程式表示。

连续性方程：

(1)

动量方程：

(2)

能量方程：

(3)

式中：u为流体速度；E为比内能；μt为湍流黏度；g为重力加速度；φ为黏性引起的能量耗散；下标i、j为方向。

1.3 网格无关性与模型验证

p=8 MPa，G=260 kg/(m2·s)，qw=35 kW/m2时不同网格节点数的上母线轴向壁温(Tw)见图4。由图4可知，当网格节点数大于329万时，壁温曲线几乎无偏差，对后续计算结果影响不大，所以最终选定网格节点数为329万。

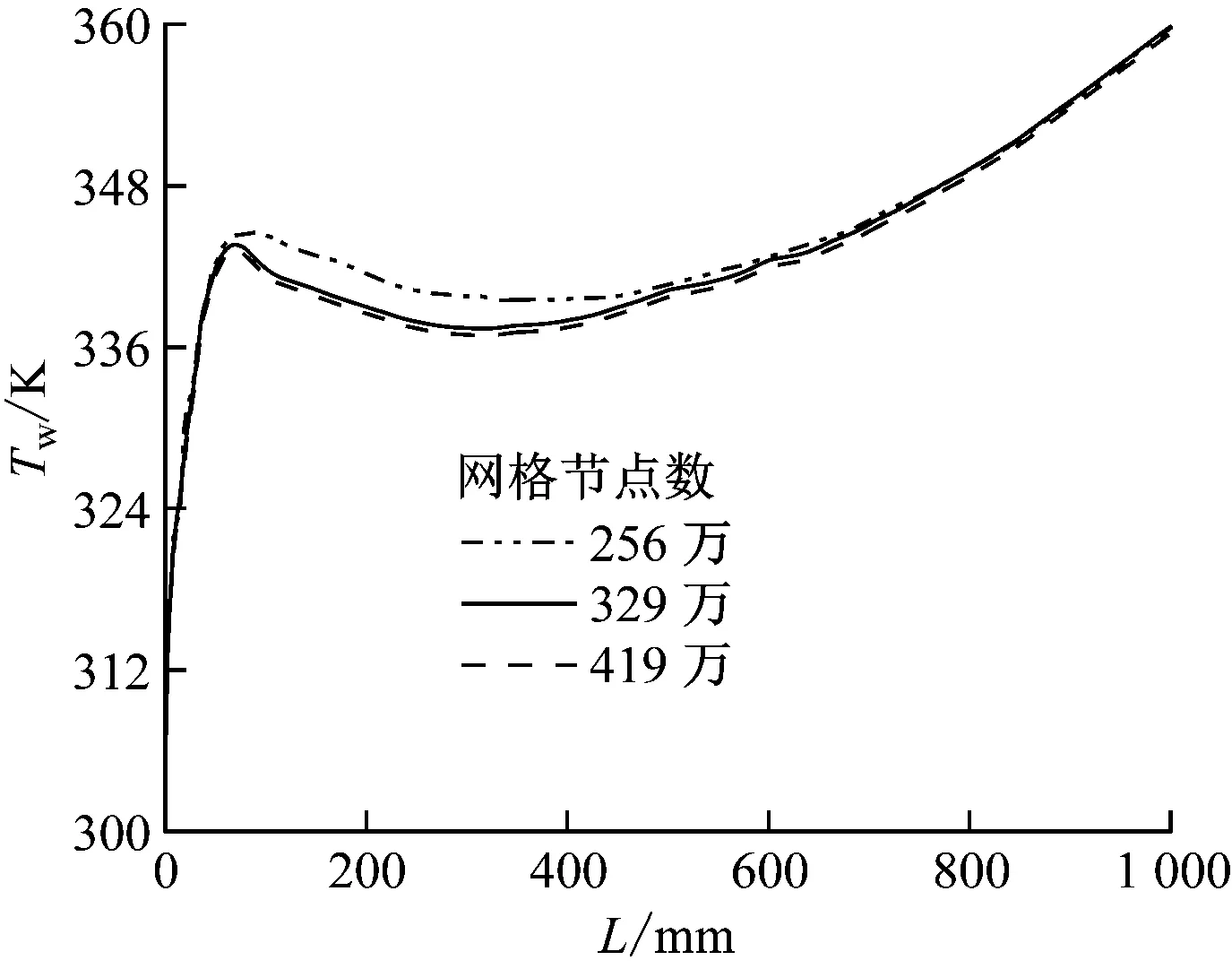
图4 不同网格节点数的上母线轴向壁温

为了验证数值计算的合理性和准确性，选用Adebiyi等[10]的实验工况(p=7.59 MPa,G=384.4 kg/(m2·s)，qw=15.1 kW/m2)进行模型验证。母线温度模拟结果与实验结果的对比如图5所示。由图5可知，模拟结果与实验结果的变化趋势基本一致，因此所采用的数值模型可以较好地预测水平管中超临界压力下CO2的传热特性。

图5 母线温度模拟结果与实验结果的对比

2 计算结果与讨论

2.1 热流密度对传热的影响

为了获得不同运行参数下水平管内超临界CO2的传热特性，本节分别考察了2种质量流量下不同热流密度对管壁传热的影响。

对流传热系数hw定义为：

(4)

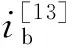
(5)

式中：Tb为主流温度；qw为壁面热流密度；A为水平管横截面面积；i为当地流体焓值。

不同热流密度下壁温与传热系数随主流焓值的变化曲线如图6所示。

由图6(a)可知，上母线的壁温在入口处突增，出现尖锐峰值，即发生局部传热恶化，随后壁温下降，在拟临界焓值(ipc)附近时趋于平缓；下母线的壁温随着主流焓值ib的增大而单调上升。随着热流密度的增大，上母线的壁温峰值逐渐上升，与下母线的壁温差也随之增大。当qw=40 kW/m2时，上下母线壁温差达到186 K。在图6(a)中，Tb为302～378 K，Tw为304～520 K。流体受重力影响产生浮升力，浮升力对换热的影响随着热流密度的增大而增强，导致上下母线出现较大温差。

由图6(b)可知，传热系数与温度的变化趋势相反，上母线传热系数(hw,t)始终低于下母线的传热系数(hw,b)，上母线传热系数在壁温峰值处达到谷值，随着主流焓值的增大，换热逐渐恢复，并在拟临界焓值附近达到最大值。热流密度越大，传热恶化程度越高，传热系数越小。随着主流焓值ib的增大，下母线传热系数呈先增大后减小的趋势，在主流焓值低于拟临界焓值处出现传热系数峰值，即发生传热强化，其出现峰值的位置比上母线更早，随着热流密度增大，传热系数减小，峰值降低。

由图6(c)和图6(d)可知，在G=260 kg/(m2·s)条件下，上母线壁温同样在入口处达到峰值，对应的传热系数位于最低点，随后换热恢复，在ib≈330 kJ/kg处达到峰值。在图6(c)中，Tb为302～320 K，Tw为304～377 K。随着热流密度的增大，换热恢复程度降低，传热系数减小。下母线的壁温和传热系数与G=140 kg/(m2·s)时的变化规律相同，不再赘述。与G=140 kg/(m2·s)相比，G=260 kg/(m2·s)时的上下母线壁温差减小，浮升力效应减弱，上母线传热恶化现象有所缓解。

2.2 浮升力对传热的影响

上下母线的温度分布不均匀可充分说明浮升力对换热的影响，针对水平管内浮升力效应，目前仍没有统一的判别式和阈值。吕海财等[15]通过对比发现Kim等[16]提出的浮升力(BK)判别式能较好地反映超临界压力下CO2在小管径通道内的传热过程；蒲星宇等[17]认为判断浮升力产生的原因应分为qw/G较小和qw/G较大这2种情况，计算浮升力时应选取上母线温度，并得出BP[18]判别式更适合壁温差较大工况的结论。选取BK和BP来评估管内浮升力效应，计算公式如下：

(6)

(7)

(8)

(9)

(10)

(11)

当BP>1时，不可忽略浮升力。BP公式构成中包含d4，管径对浮升力产生较大影响。在已有文献中，普遍得出了大管径模型中浮升力较强的结论[19]。对于小管径的几何模型，浮升力对传热也有影响[20]。G=140 kg/(m2·s)和G=260 kg/(m2·s)时，2种判别式下上母线浮升力随热流密度变化的曲线如图7所示，其中ΔT为上下母线壁温差。由图7可知，2种判别式下浮升力均随热流密度的增大而增大，但曲线趋势不同。BK的变化趋势为浮升力峰值出现在拟临界焓值处，而BP的变化趋势为浮升力在发生传热恶化的位置处出现尖锐峰值，然后下降，直到加热结束。另外，浮升力在拟临界焓值点前下降较快，而在拟临界焓值点后下降较平缓。

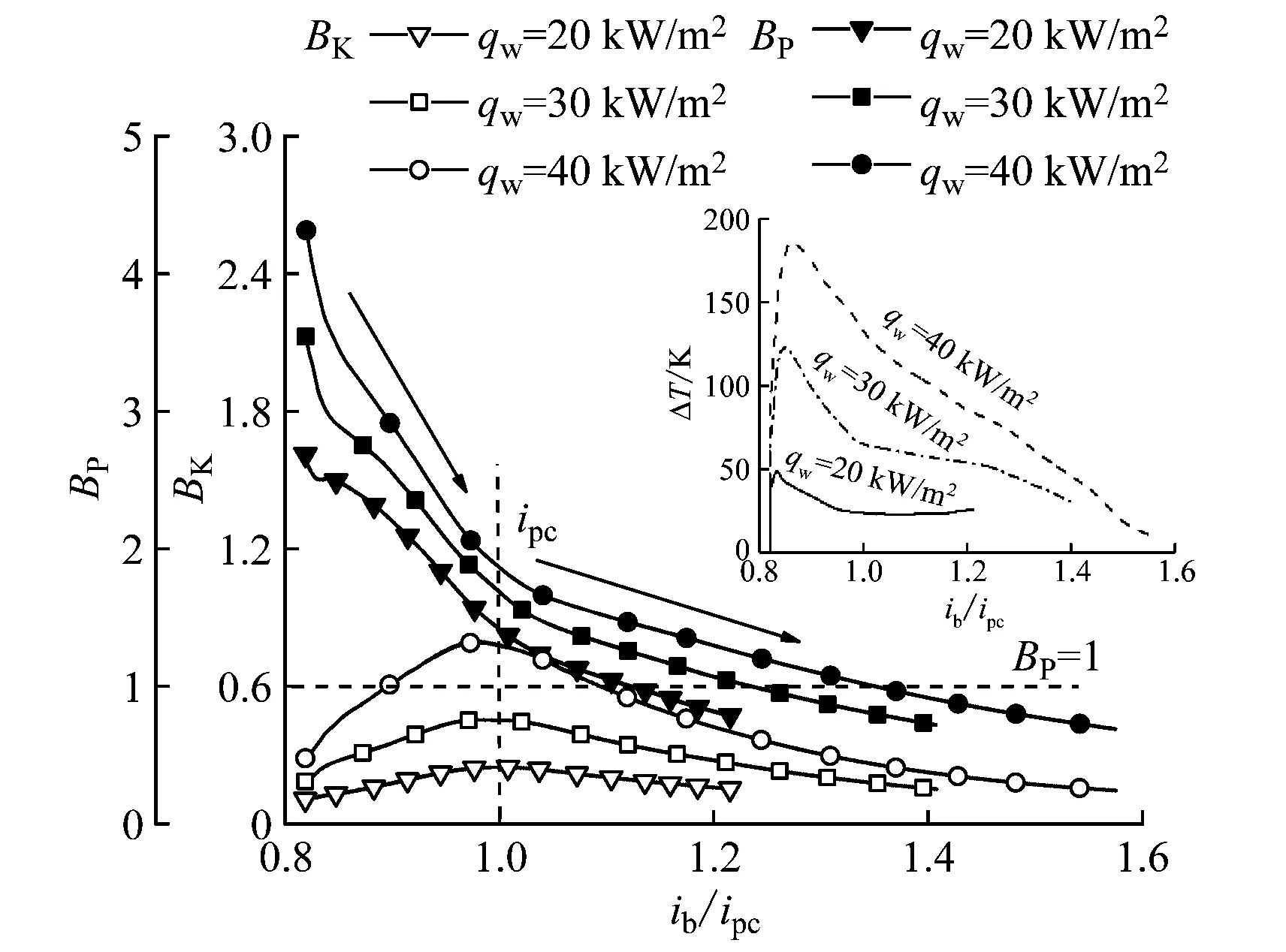
(a) G=140 kg/(m2·s)

比较图7(a)与图7(b)发现，G=140 kg/(m2·s)时的浮升力更强，峰值更明显，所以壁温差越大浮升力越强，且浮升力在峰值后的下降速度更快。而G=260 kg/(m2·s)时，3种热流密度下的BP均小于1，所以此工况下的浮升力可忽略。

浮升力与壁温差的曲线趋势大致相同，壁温差的峰值可大致代表浮升力的峰值。所以在本文2种工况下，BP更能反映浮升力的分布，壁温差大小可反映浮升力的强弱。

2.3 压力对浮升力的影响

在G=140 kg/(m2·s)、qw=30 kW/m2条件下，压力分别为8.0 MPa、8.5 MPa和9.0 MPa时的浮升力及CO2物性参数如图8所示。由图8可以看出，浮升力随着压力的增大而下降，对传热的影响也逐渐减弱。这是由于当压力远离临界压力时，CO2的物性剧烈变化程度减小。从图8可知，物性随着压力的变化而变化，比热容在拟临界温度点附近突升幅度随压力的增大而减小，而压力对传热的影响主要取决于比热容。因此，增大压力可抑制传热恶化，使浮升力效应减弱。

图8 不同压力下浮升力随主流焓值的变化曲线

2.4 水平管传热特性机理

选取G=140 kg/(m2·s)，qw=30 kW/m2的工况，取ib=280 kJ/kg(入口处)、287.3 kJ/kg(壁温峰值处)、320 kJ/kg、340 kJ/kg(拟临界焓值)、360 kJ/kg、400 kJ/kg和440 kJ/kg 7个典型截面，各截面的密度、温度、湍动能(k)及速度分布如图9所示。

由图9(a)和图9(b)可知，上母线聚集着高温且密度小的流体，产生了温度梯度，而下母线处的流体因重力作用密度较大，温度较低，其中在ib=287.3 kJ/kg处的壁温差和密度差最大，对应的截面密度分布如图10所示。由图10可知，因浮升力效应各截面密度出现明显的分层现象，随着加热的进行，总密度逐渐减小，分层效果逐渐减弱，上下母线密度差也逐渐减小。

由图9(c)和图9(d)可知，湍动能和速度不完全呈轴对称，湍动能随着加热的进行逐渐增大，顶部湍动能稍小于底部湍动能，底部湍动能强化了下母线的传热。ib=287.3 kJ/kg处的顶部密度低，所以对应的顶部速度较小，在换热恢复期间，流体速度逐渐增大，且速度梯度增加，上下母线的速度逐渐接近，在加热即将结束时，顶部和底部的速度接近相同。

3 结 论

(1) 热流密度的增大可导致传热恶化的发生。热流密度越大，传热恶化现象越明显，同时上下母线的壁温差会随热流密度的增大而增大。

(2) 在G=140 kg/(m2·s)条件下，浮升力导致上下母线壁温差较大；在G=260 kg/(m2·s)条件下，浮升力可忽略。BP判别式更能反映本文工况下浮升力的分布，同时壁温差大小可大致反映浮升力的强弱。

(3) 压力增大使CO2物性变化趋于平缓，浮升力随着压力的增大而下降，因此增大压力可抑制传热恶化。

(4) 由典型截面物性分布可知，在发生传热恶化处(ib=287.3 kJ/kg)，密度分层明显且温度梯度较大，上母线的速度和湍动能稍低于下母线，反映了上下母线不同的传热机理。