基于模糊Domain基的连续扩张

饶三平

(南昌工程学院 理学院，江西 南昌 330099)

Domain理论是程序语言指称语义学的数学基础。序与拓扑的相互结合，相互作用是这一理论的基本特征。正是由于Domain理论的这一特征及其与计算实践的紧密联系，从70年代Scott开创Domain理论以来[1]，一直受到数学和计算机科学领域内诸多学者的关注，更成为拓扑学的一个重要的研究方向。

量化Domain理论主要是为并发式程序语言提供数学语义模型。经过多年来的发展，取得了迅速发展。Zhang和Fan引进L-Fuzzy拟序集构成量化Domain理论的基本框架[2]，促进了量化Domain理论的发展。他们首先定义模糊偏序，实质上是非空集上的程度映射，然后再研究L-Fuzzy的一些基本性质。基于完备剩余格，Yao和Shi研究了模糊dcpos和它上面的连续性[3-4]，并对模糊dcpos上的模糊Scott拓扑进行了系统的研究。此外，从范畴的角度，Hofmann和Waszkiewicz对量化Domain理论也进行了研究[5-6]。基于可换单位Quantale上的Ω-范畴，Lai和Zhang也研究了量化Domain理论[7]。可以说，这些研究都是对经典Domain理论进行了进一步推广。

在对量化Domain理论研究的过程中，最重要的研究对象无疑是模糊Domain[8]。那么怎样刻画这么一个重要概念显得尤为重要。众所周知，在经典的Domain理论中，基和Galois联络扮演着重要角色，其结果不仅仅体现在刻画Domain，对研究Domain的其它一些性质也起了重要作用。那么，在模糊Domain中，是否有类似的概念及性质？为此，本文进行了相应的研究。

1 预备知识

本文选取完备剩余格作为格值，完备剩余格L是一种代数结构，它满足：

(1)(L，∧，∨，*，→，0，1)是完备格，最小元为0，最大元为1；

(2)(L，*，1)是可交换的monoid，基中1是单位元，即∀a∈L，a*1=a；

(3)*，→构成Galois联络，即∀a，b，c∈L，a*b≤c⟺a≤b→c。

有关详细完备剩余格的知识可参考文献[9]，若无特别声明，本文中L表示完备剩余格。下面列出运算*，→的一些基本性质。

引理1[9]设L是完备剩余格，则∀a，b，c∈L，下列式子成立：

(I1) 0*a=0且1→a=a；

(I2)a≤b⟺a→b=1；

(I3) (a→b)*(b→c)≤a→c；

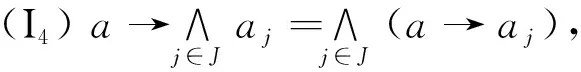
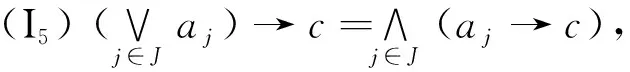
(I6)a→(b→c)=b→(a→c)=a*b→c；

(I7)a*(a→b)≤b.

设X为一非空集合，X上的模糊子集就是从X到L上的映射，X上的所有模糊子集记为LX。∀A，B∈LX，A和B之间的相等可以通过一般映射之间的相等来定义，也就是说，A=B⟺∀x∈X，A(x)=B(x)。

定义1[9]X上的模糊关系e是X×X上的模糊子集，即e：X×X→L。X上的模糊关系e称为是模糊偏序。若e还满足：

(1)∀x∈X，e(x，x)=1；

(2)∀x，y，z∈X，e(x，y)*e(y，z)≤e(x，z)；

(3)∀x，y∈X，e(x，y)=e(y，x)=1⟹x=y.

称(X，e)为模糊偏序集。若e是X上的模糊偏序，A∈LX称为模糊上集。若∀x，y∈X，A(x)*e(x，y)≤A(y)，A∈LX称为模糊下集。若A(x)*e(y，x)≤A(y)。

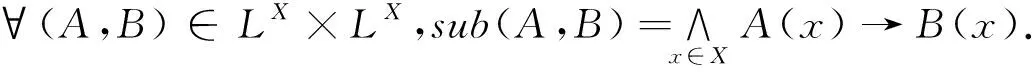
定义2[2]设(X，e)是模糊偏序集，x0∈X称为模糊子集A的并，记为x0=凵A。若满足下列条件：

(1)∀x∈X，A(x)≤e(x，x0)；

在引理2中，若A=↓x，则

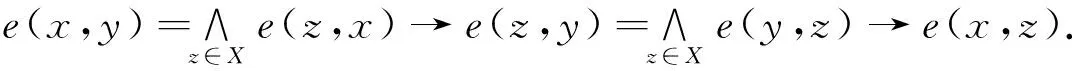
定义3[3]设(X，e)是模糊偏序集，模糊子集D∈LX为模糊定向的。 若它满足：

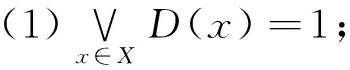
记X上所有的模糊定向子集为DL(X)。称模糊偏序集(X，e)为模糊dcpo。若∀D∈DL(X)，凵D存在。

定义4[3]设(X，e)是模糊dcpo。∀x，y∈X，：X×X→L定义如下：

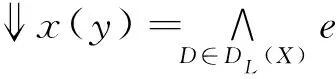
定义5[3]模糊dcpo(X，e)称为模糊Domain若它满足：∀x∈X，

(2)x=凵x.

此外，∀x，y∈X，定义映射k：X→LX如下：k(x)(y)=e(y，x)*y(y)。若∀x∈X，k(x)是模糊定向子集且满足x=凵k(x)，则称(X，e)为模糊代数Domain。

引理3[3]设(X，e)是模糊dcpo，则∀x，y，u，v∈X，下列式子成立：

(2)e(u，x)*y(x)*e(y，v)≤v(u).

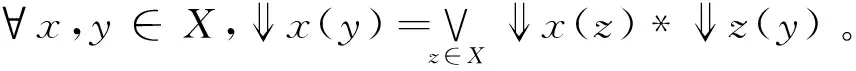
引理5[4]设(X，e)为模糊dcpo，∀x∈X，若存在模糊定向子集A满足x=凵A和A≤x，则x是模糊定向子集且x=凵x。

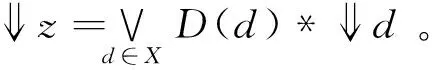
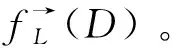
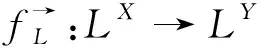
定义7[10]设(X，eX)、(Y，eY)为模糊偏序集，f：(X，eX)→(Y，eY)、g：(Y，eY)→(X，eX)为模糊单调映射。称有序对(f，g)为(X，eX)和(Y，eY)之间的模糊Galois联络，若∀x∈X，y∈Y，eY(y，f(x))=eX(g(y)，x)，其中，称f为g的上(左)伴随；对偶地，g为f的下(右)伴随。

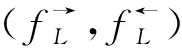
2 连续扩张

下面要建立基于模糊Galois联络的连续扩张。为此，首先提出以下的概念。

定义8在模糊dcpo(X，e)中，称B⊆X为X的基，若它满足：

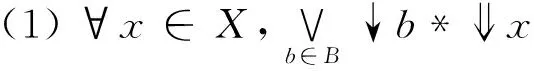
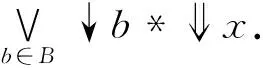
下面用上面介绍的定义来刻画模糊Domain。

定理1对于一个模糊dcpo来说，它有基当且仅当它是模糊Domain。

证明充分性：易证X⊆X是X的基，显然，它是最大的基。

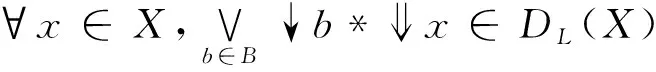
定理2在模糊Domain(X，e)中，B⊆X，下列命题等价：

(1)B是X的基；

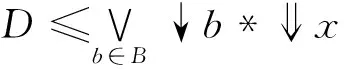
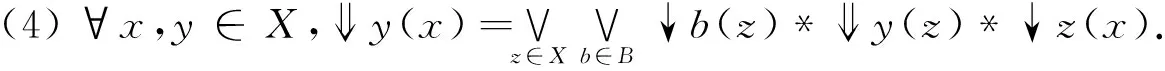
证明(1)⟹(2)，由定义8可得。

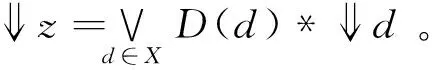
事实上，∀x，y∈X，

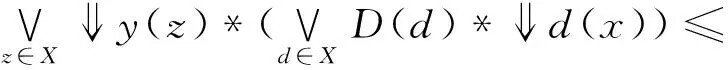
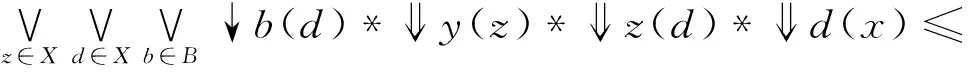
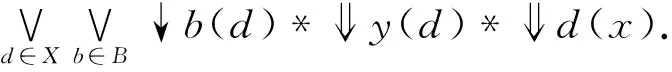
(3)⟹(4)，∀x，y∈X，有

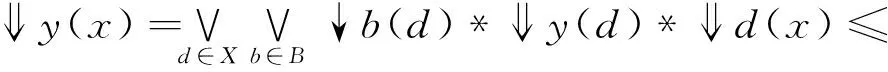
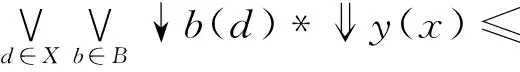
y(x).

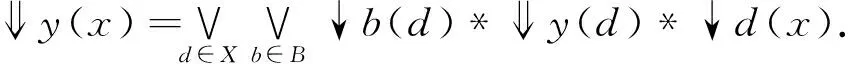
(4)⟹(1)，若(4)成立，下证B是X的基，∀y∈X，

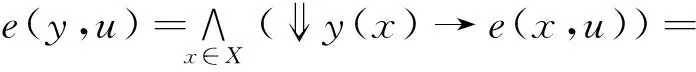
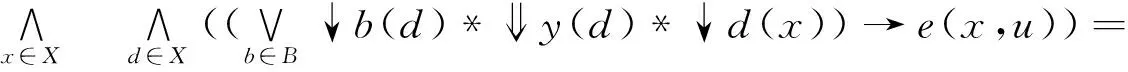
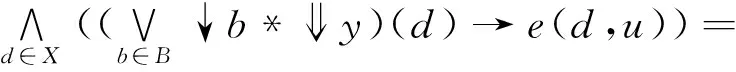
e(凵

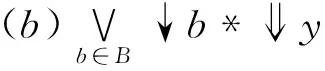
首先，∀a′，b′∈X，

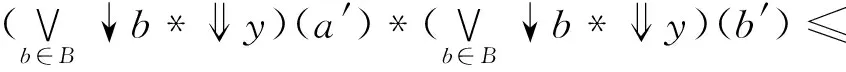
y(a′)*y(b′)≤

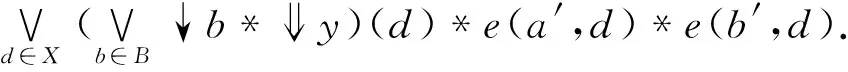
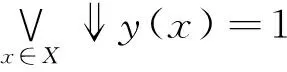
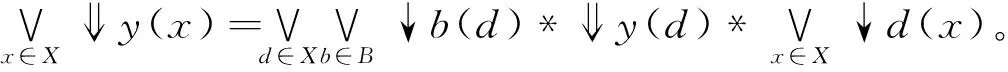
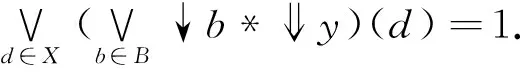
定理3在模糊Domain(X，e)、(Y，e)中，B⊆X、C⊆Y分别是(X，e)、(Y，e)的基，(g，d)是从(B，e)到(C，e)之间的模糊Galois联络。则存在唯一的从(X，e)到(Y，e)的模糊Galois联络(G，D)，且G是g的连续扩张。

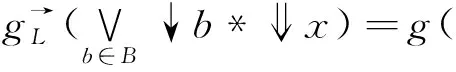
同理，∀y∈C，D(y)=d(y)，易验证G是模糊连续的，下证(G，D)是从(X，e)到(Y，e)之间的模糊Galois联络。 ∀x∈X，y∈Y，

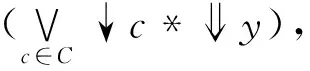
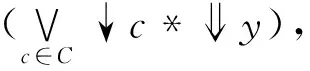
e(D(y)，x).

唯一性是显然的。

3 结束语

本文基于模糊dcpo，给出了基的概念，从而获得模糊Domain的等价刻画，同时借助于模糊Galois联络，给出了模糊Domain基的连续扩张。对于模糊Domain基的连续扩张的研究，不仅丰富了模糊Domain的理论知识，拓展了模糊Galois联络的应用，还为其它模糊对象的相应扩张提供了一种可行的方法。