基于系统动力学的长期护理保险筹资费率水平研究——以江西省上饶市为例

陆伟锋，陈 欢，杨碧琴，李 春，高 威

(1.南昌工程学院 工商管理学院，江西 南昌 330099；2.江西科技学院 财经学院，江西 南昌 330098)

为积极应对人口老龄化问题，2016年人力资源与社会保障部办公厅发布《关于开展长期护理保险制度试点的指导意见》(人社厅发[2016]80号)，确定首批15个试点城市。根据2020年第七次人口普查统计结果，我国60岁及以上人口为26 402万人，其中65岁及以上人口为19 064万人，人口占比分别为18.7%和13.5%，表明我国人口老龄化程度进一步加深。在前期试点的基础上，2020年国家医保局会同财政部印发《关于扩大长期护理保险制度试点的指导意见》(医保发〔2020〕37号)(以下简称《扩大试点意见》)，将试点范围进一步扩大到49个，着眼于建立独立险种及与经济社会发展和保障水平相适应的筹资动态调整机制。

长期护理保险制度顺利推行的关键在于可持续筹资机制的构建。筹资机制因涉及多方利益主体，是最难选择和决策的。目前，学者从筹资对象、筹资渠道、筹资水平及费率测算等方面对筹资机制进行研究。首先，筹资对象的确定面临着覆盖全民和覆盖特定群体这两个选择。覆盖全民有利于做大长期护理保险资金池，对于困难群体可以实行减免政策[1-2]；覆盖特定群体会导致长期护理保险筹资能力弱化，不利于保险的可持续发展，同时被排除在外的人群一旦面临失能，将要承受巨大的财务和心理压力。其次，学者们基本一致认为要采取多元筹资渠道，主要由政府、企业与个人共同承担。我国长期照护资金缺口庞大，在国家投入补贴的同时，采用多元化的资金筹措方式才有可能妥善解决这一问题[3]。同时应体现权利与义务对应的原则，实行个人、社会(企业)和政府“三方”付费制[4]，也可将残联基金纳入长期护理保险筹资渠道[5]，并充分发挥社会组织和慈善机构的力量，从而拓宽长期护理保险筹资渠道[6]。再次，在费率的测算方面，国外学者多采用曼联模型、减量表模型及多状态马尔可夫模型[7-9]。国内学者多采用国外的测算方法[10-11]，也有采用ILO模型对费率进行测算[12]。许多学者由于选取不同的指标体系建立长期护理保险模型测算筹资水平，导致得出的筹资水平不同，但总体筹资水平在1%～4%间[13-17]；也有研究运用现收现付制下的基金平衡法测算我国总体费率水平，当前总体缴费率为2.01%，但2030年缴费率达到3.09%，2050年高达8.61%[13]。

长期护理保险筹资机制是一个复杂的系统工程，筹资费率水平的确定是其重要的组成部分。用系统动力学的方法研究长期护理保险的筹资问题是一种好的途径。系统动力学方法应用广泛，如用系统动力学解决工业系统[18]、经济系统[19]、农业系统[20]等领域的问题。但鲜有学者用系统动力学方法对长期护理保险筹资费率水平展开研究。基于此，本文以江西省上饶市为例，运用系统动力学将长期护理保险筹资费率水平与经济社会发展水平相结合，开展仿真研究，为构建独立险种及可持续筹资机制提出政策建议。

1 流率基本入树建模法

南昌大学贾仁安教授及其团队在1998年首次提出流率基本入树建模法。该方法将复杂的大系统分解为多个小系统，接着确定各子系统的流位变量、流率变量、辅助变量等，随后构建以流率变量为树根，以流位变量为树尾，通过辅助变量将流率变量与流位变量相连接的入树模型。

定义：在系统动力学流图中，以流率为树根，以流位为树尾的入树T(t)称为流率入树[21]。其主要建模步骤如下：

(1)运用理论分析、经验诊断等对系统进行分析，确定流位流率系{[L1(t)，R1(t)]，[L2(t)，R2(t)]，…，[Ln(t)，Rn(t)]}；

(2)分析各流率变量被哪些流位变量及辅助变量影响，确定这些变量之间的关系，构建分析结果二部分图；

(3)在Vensim仿真软件中，建立流位流率系子模型，并输入各流位变量的初始值；

(4)结合实际分析的结果，从树尾流位少的入树开始，按建未建方程的流率基本入树、建仿真方程、仿真检查三部程序，分别建立以流率为树根，以流位为树尾的流率入树模型；

(5)流率基本入树模型经嵌运算生成网络流图Gi(t)，(i=1，2，3，…，n)。

本文使用Vensim软件进行仿真运算，它是一个可视化的建模工具，本文根据变量间的关系，运用该软件画出流率基本入树模型，并输入方程和参数，进行模拟仿真、分析及优化。

2 长期护理保险筹资系统入树模型构建

本文对长期护理保险筹资费率水平进行研究，运用流率基本入树建模法构建长期护理保险筹资系统动力学模型，将长期护理保险筹资系统模型分为三个子系统，分别是人口子系统、长期护理保险子系统及经济子系统。分析系统结构，确定长期护理保险筹资系统动力学模型的流位流率系如表1所示。

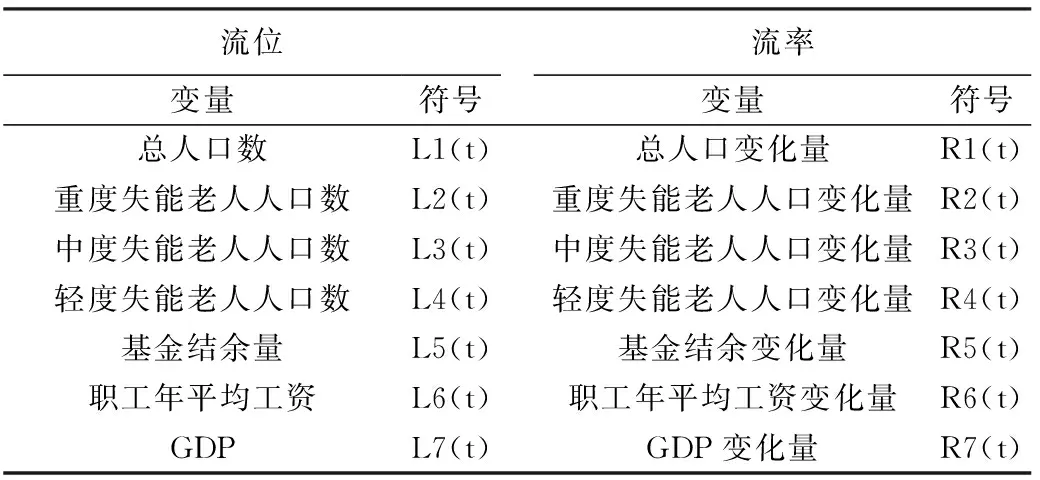
表1 长期护理保险筹资的流位流率系

2.1 人口子系统入树模型

长期护理保险着力于以专业的服务解决失能人员长期护理保障问题，以减轻失能人员家庭长期护理的事务性和经济性负担。老年人是目前长期护理保险保障的主要群体，因此，在长期护理保险筹资的人口子系统中，选取“总人口数L1(t)”“重度失能老人人口数L2(t)”“中度失能老人人口数L3(t)”及“轻度失能老人人口数L4(t)”作为流位变量，以他们相应的变化量作为流率变量。设立人口子系统的其它相关变量如表2所示，并建立T1(t)～T4(t)四棵入树构成的人口子系统入树流图(图1)。

表2 人口子系统变量及符号

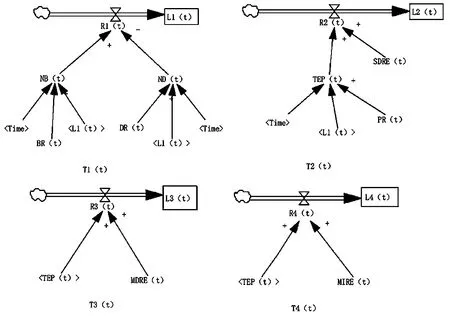
图1 人口子系统入树流图

在人口子系统入树模型中，总人口变化量R1(t)会被出生人数NB(t)及死亡人数ND(t)影响，同时，出生人数NB(t)和死亡人数ND(t)受人口出生率BR(t)、人口死亡率DR(t)及总人口数L1(t)影响，其中，人口出生率BR(t)、人口死亡率DR(t)是时间的表函数。不同失能程度的失能老人是长期护理保险的主要保障对象，因此在人口子系统入树模型中，轻、中、重度失能老人的人口数是该子系统的重要影响因素，轻、中、重度失能老人的变化量分别与其相应的失能率及老年人口总数TEP(t)有关。

2.2 长期护理保险子系统入树模型

长期护理保险子系统是按照“以收定支，收支平衡，略有结余”的原则运行，基金的结余状况关系到长期护理保险基金能否正常持续运行。因此，在长期护理保险筹资的长期护理保险子系统中，“基金结余量L5(t)”作为流位变量，“基金结余变化量R5(t)”作为流率变量，建立T5(t)这颗入树构成的长期护理保险子系统入树流图(图2)。设立长期护理保险子系统的其它相关变量如表3所示。

图2 长期护理保险子系统入树流图

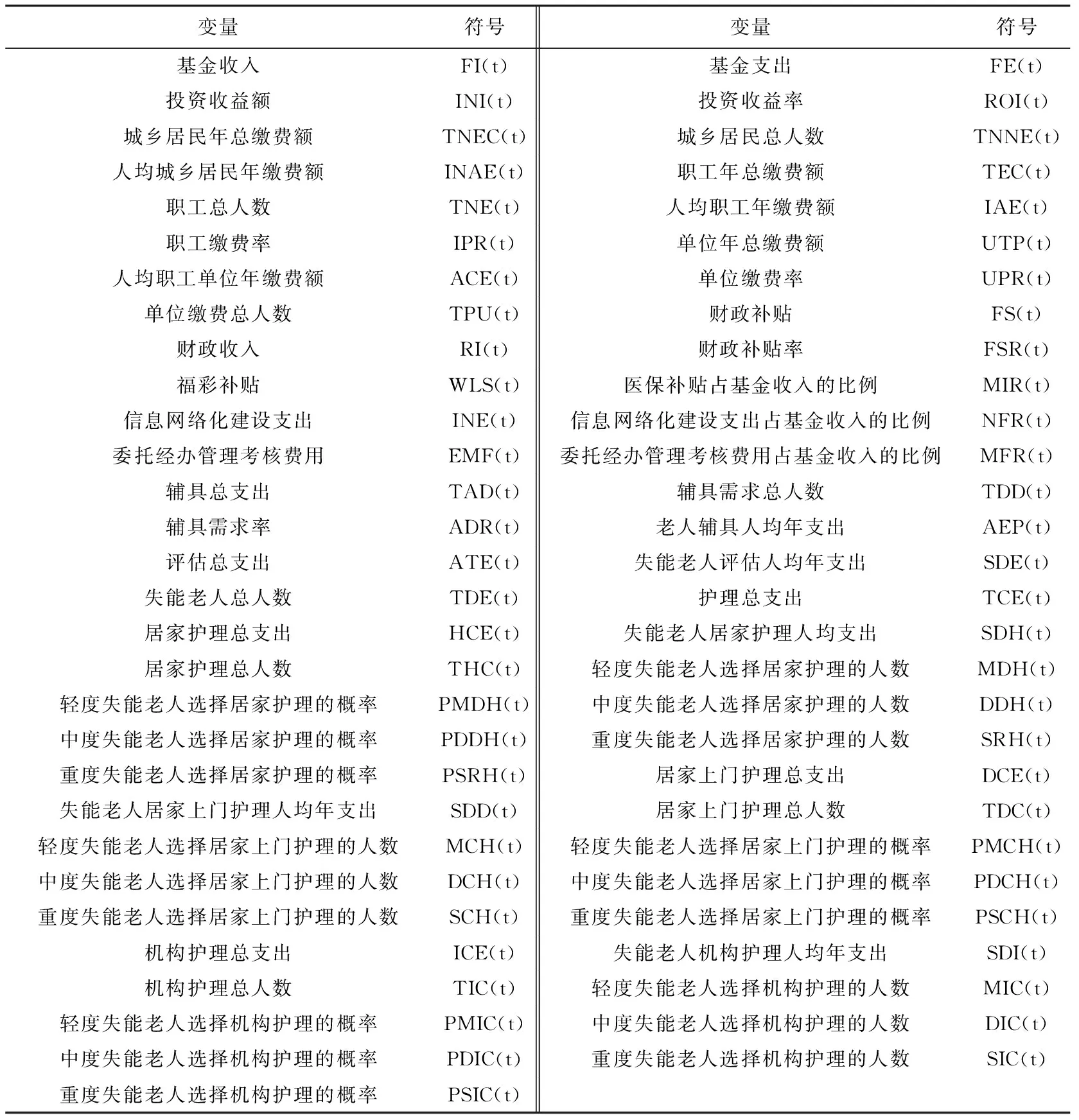
表3 长期护理保险子系统变量及符号

基金结余量的变化是由基金收入FI(t)和基金支出FE(t)引起的。基金结余变化量可由式(1)计算：

R5(t)=FI(t)-FE(t).

(1)

长期护理保险的筹资渠道由个人缴费、单位缴费、财政补贴、医保补贴、福彩补贴等构成。基于此，本文将长期护理保险基金收入来源确定为城乡居民年总缴费额TNEC(t)、职工年总缴费额TEC(t)、单位年总缴费额UTP(t)、财政补贴FS(t)、福彩补贴WLS(t)、投资收益额INI(t)和医保补贴占基金收入的比例MIR(t)。基金收入可由式(2)计算：

FI(t)=[TNEC(t)+TEC(t)+UTP(t)+FS(t)+WLS(t)+INI(t)]/[1-MIR(t)].

(2)

为了与经济发展水平相联系，模型中筹资方式为定比筹资，人均职工年缴费额IAE(t)及人均职工单位年缴费额ACE(t)是由职工及职工单位按照职工年平均工资L6(t)的一定比例缴纳。人均职工年缴费额及人均职工单位年缴费额可由式(3)～(4)计算：

IAE(t)=IPR(t)×L6(t)，

(3)

ACE(t)=UPR(t)×L6(t).

(4)

投资收益额INI(t)来源于基金结余量L5(t)的利息收入。投资收益额可由式(5)计算：

INI(t)=ROI(t)×L5(t).

(5)

长期护理保险基金支出主要用于对失能人员的评估、护理费用的补贴、提供辅具用品、信息网络化建设等，基于此，本文将长期护理保险支出确定为护理总支出TCE(t)、评估总支出ATE(t)、辅具总支出TAD(t)、委托经办管理考核费用EMF(t)、信息网络化建设支出INE(t)等构成，因此基金支出可由式(6)计算：

FE(t)=INE(t)+EMF(t)+TAD(t)+ATE(t)+TCE(t).

(6)

护理总支出TEC(t)由居家护理总支出HCE(t)、居家上门护理总支出DEC(t)以及机构护理总支出ICE(t)构成。护理总支出可由式(7)计算：

TEC(t)=HCE(t)+DCE(t)+ICE(t).

(7)

评估总支出ATE(t)与失能老人总人数TDE(t)及失能老人评估人均年支出SDE(t)有关。评估总支出可由式(8)计算：

ATE(t)=TDE(t)×SDE(t).

(8)

辅具总支出TAD(t)与辅具需求总人数TDD(t)及老人辅具人均年支出AEP(t)有关。辅具总支出可由式(9)计算：

TAD(t)=TDD(t)×AEP(t).

(9)

委托经办管理考核费用EMF(t)和信息网络化建设支出INE(t)分别按不超过基金收入FI(t)的一定比例支付，其中信息网络化建设预计3年完成，建成后，停止支付信息网络建设支出。委托经办管理考核费用和信息网络化建设支出可由式(10)～(11)计算：

EMF(t)=MFR(t)×FI(t)，

(10)

INE(t)=NFR(t)×FI(t)，if time>2022.

(11)

2.3 经济子系统入树模型

经济因素对长期护理保险筹资费率水平有决定性的影响作用，发达的经济意味着政府的财政能力和资金的筹集能力较强，能够持续地为长期护理保险制度提供资金支持。因此，在长期护理保险筹资的经济子系统中，选取“职工年平均工资L6(t)”和GDPL7(t)”作为流位变量，“职工年平均工资变化量R6(t)”及“GDP变化量R7(t)”作为流率变量，设立经济子系统的职工年平均工资增长率AGRE(t)和GDP增长率GR(t)，建立T6(t)和T7(t)两颗入树构成的经济子系统入树流图(图3)。

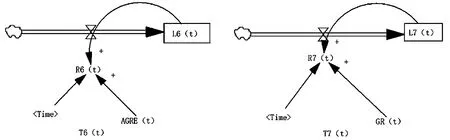
图3 经济子系统入树流图

在经济子系统入树模型中，职工年平均工资变化量R6(t)主要受职工年平均工资L6(t)和职工年平均工资增长率AGRE(t)影响。GDP变化量R7(t)受GDPL7(t)和GDP增长率GR(t)影响，其中职工年平均工资增长率AGRE(t)和GDP增长率GR(t)，是时间的函数。

3 基于上饶市的模型仿真

上饶市作为首批试点城市之一，于2016年11月开始开展长期护理保险试点工作，将辖区内所有参加城镇职工医疗保险的人纳入长期护理保险的参保范围，将筹资标准暂定为每人每年100元。为通过评估的失能人员提供居家自主照料、居家上门护理以及机构内护理服务。2019年提出建立全市统一、覆盖全体城镇职工和城乡居民的长期护理保险制度，并将筹资标准调整为每人每年90元，其中个人缴纳50元，医保基金划转35元，单位或财政补助5元。但个人缴纳部分实际上是从医保个人账户中扣除的，医保基金实际上缴费高达每人每年85元，这使得长期护理保险基金过于依赖医保基金，再加上城乡居民参保基数大，给长期护理保险基金的现有筹资渠道带来了巨大的压力，不利于长期护理保险的可持续发展。

3.1 参数设定

以2017年为仿真模拟的基期，2020—2035年为预测期，步长为1年，系统的历史数据主要来源于2015—2020年江西省统计年鉴、上饶市人力资源与社会保障局官网等权威网站、参考上饶市国民经济和社会发展统计公报等资料。目前上饶市长期护理保险仅为重度失能老人提供长期护理保险服务，本文假设从2022年开始长期护理保险范围扩大到中度失能老人及轻度失能老人。

在模型运行前，需要对一些变量参数赋值、本文根据CHARLS数据对样本按照barthel量表测算使用stata16.0进行描述性统计。计算得出65岁及以上老年人的轻度失能率、中度失能率、重度失能率分别为35.3%、2.42%及19.67%。单位和个人按照1∶1的比例负担长期护理保险[16]。上饶市目前采用定额筹资的方式，但难以适应经济水平的发展。定比筹资测算可以与经济发展水平相联系，因此本文采用定比筹资的测算方法。在长期护理保险实施以来，医保基金作为长期护理保险基金的重要来源，目前医保补贴占基金收入的比例高达94.4%，个人及单位并未实现真正的缴费，为构建独立险种。本文根据目前上饶市的缴费规定，将个人及单位缴费与医保补贴分离，把医保补贴占基金收入的比例调整为38.9%。系统的其余变量分别用赋值、回归分析和表函数法来设置，使模型能更加准确的模拟现实系统。如表4为系统部分参数及方程式设置。

表4 系统部分参数及初始赋值

3.2 模型检验

建立模型后，需要对模型进行检验，以确定模型结果能准确的描述现状并解决存在的问题。基于2017年的数据完成参数的有效性检验(如表5)。GDP的真实值与拟合值之间的最大误差为3.21%，拟合情况好。总人口数和职工年平均工资的误差均在2%以内，表明模型的结构和变量选取合理，能够运用系统动力学模型对长期护理保险筹资费率水平进行研究。

表5 系统模拟误差检验

3.3 上饶市长期护理保险筹资系统现状仿真

随着我国人口老龄化的加剧，失能人口不断增加，对长期护理服务的需求也呈上升趋势。自2016年底我国开展长期护理保险试点工作后，上饶积极探索构建完善的长期护理保险系统。本文通过系统动力学模型按照上饶目前长期护理保险的相关政策进行仿真，预测了2020—2035年长期护理保险基金的结余情况，如图4所示，长期护理保险基金结余在制度刚开始实施时是在稳定的增长，在经过缓慢地增长后便迅速下降，到2028年基金结余量为负。如图5所示，失能老人的数量将会逐年上升，为了使长期护理保险基金独立且持续地运营，必须采取一定的干预措施。

图5 失能老人人口数仿真结果

4 模型仿真分析

考虑到上饶市各地区人口差异大、财政收入差距大，因此财政补贴率固定为0.1%。每年的福彩补贴固定为1000万元，投资收益率固定为央行活期存款基准利率0.35%。城乡居民缴费额由职工缴费额及单位缴费额共同确定，因此本文通过对职工缴费率、单位缴费率、医保补贴占基金收入的比例的调控，对长期护理保险进行模拟，探究长期护理保险基金是否能独立且可持续的运行。

4.1 对职工缴费率和单位缴费率的仿真分析

本模型中个人和单位是按照1∶1的比例共同缴纳长期护理保险费用，模型中职工缴费率和单位缴费率的初始值为0.1%。本文以2035年为比较节点，设置5个等级的调控方案。每个调控(如表6所示)，比较不同职工缴费率和单位缴费率下基金结余量的变化情况，仿真结果如图6所示。

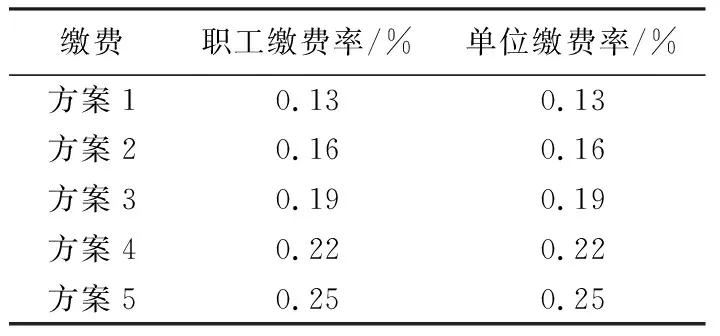
表6 职工缴费率和单位缴费率的仿真方案

如图6所示，职工缴费率和单位缴费率越高，基金结余量越多，基金能持续的时间也越长。以上5种仿真方案结果显示，在2035年时结余量都为正值。但在方案1下，基金结余量的曲线处于迅速下降阶段，虽然仿真结果显示在2035年依旧为正值，但很快基金结余量将变成负值。方案2在2035年时，基金结余量曲线快要接近最大值，处于缓慢上升阶段，而方案3～5在2035年时，基金结余量曲线都处于快速上升阶段。因此，考虑到基金的可持续性及基金的收支原则，在保持其他参数不变的情况下，应该选择方案2。

4.2 对医保补贴占基金收入的比例的仿真分析

按照目前上饶市长期护理保险的筹资政策，实现个人和单位独立缴费后，医保补贴占基金收入的比例为38.9%。2020年《扩大试点意见》提出“着眼建立独立险种、独立设计、独立推进”，为提高长期护理保险基金的独立性，本文以2035年为节点，设计了四个仿真方案，将医保补贴占基金收入的比例分别设置为30%、20%、10%及0%，比较不同医保补贴占基金收入的比例下基金结余量的变化，仿真结果如图7所示。

如图7所示，医保补贴占基金收入的比例越低，基金结余量为负的速度越快。在方案1下，基金结余量将在2027年时为负值；在方案2下，基金结余量将在2026年时为负值；在方案3下，基金结余量将在2025年时为负值；方案4下，基金结余量将在2025年时为负值。因此，在保持其他参数不变的情况下，长期护理保险无法摆脱对医保补贴的依赖。

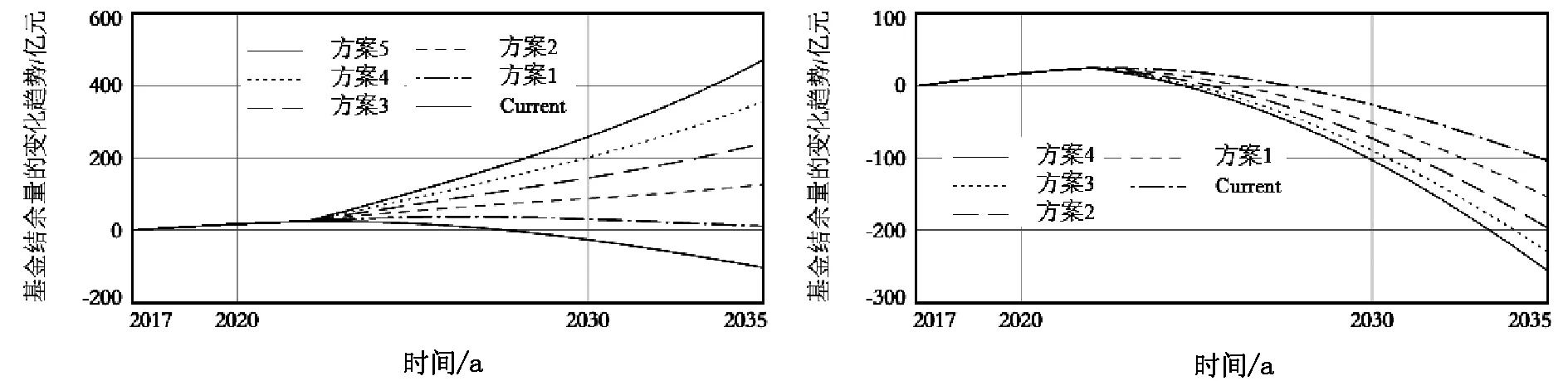
图6 不同职工缴费率和单位缴费率下 基金结余量趋势预测图 图7 不同医保补贴占基金收入的比例下 基金结余量趋势预测图

4.3 医保补贴占基金收入的比例为30%、20%、10%和0%下的综合调控策略

通过对职工缴费率及单位缴费率和医保补贴占基金收入的比例的仿真分析，设置5种综合仿真方案(如表7所示)，探究当医保补贴占基金收入的比例分别为30%、20%、10%、0%时，不同职工缴费率和单位缴费率对长期护理保险基金结余量变动趋势影响如图8所示。

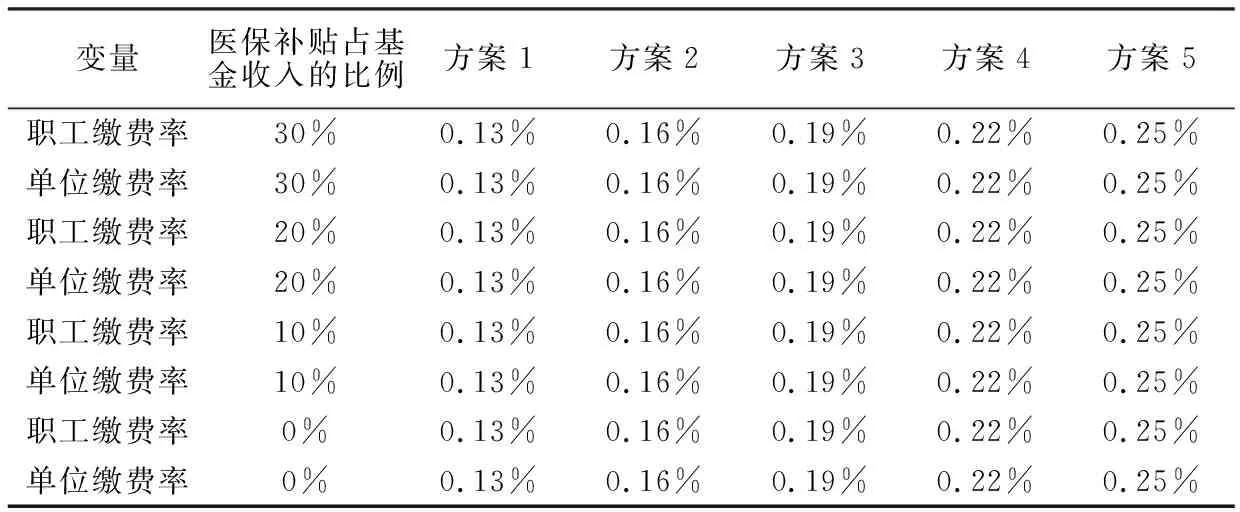
表7 综合仿真方案

如图8(a)所示，当医保补贴占基金收入的比例为30%时，在方案1下，基金结余量在2030年时就为负值，到2035年时，资金缺口高达53亿。在方案2～5下，基金结余量在2035年时为正值，但考虑到基金的可持续性及基金的收支原则，此时方案2最优；如图8(b)所示，当医保补贴占基金收入的比例为20%时，在方案1和2下，基金结余量在2030年时为负值，在方案3～5下，基金结余量在2035年时为正值，且在方案3下，基金结余量曲线处于平稳状态，同时考虑到基金的可持续性及基金的收支原则，此时方案3最优；如图8(c)所示，当医保补贴占基金收入的比例为10%时，在方案1和2下，基金结余量在2030年时为负值。在方案3～5下，基金结余量在2035年时为正值，且在方案4下，基金结余量曲线处于缓慢上升阶段，同时考虑到基金的可持续性及基金的收支原则，此时方案4最优；如图8(d)所示，当医保补贴占基金收入的比例为0%时，在方案1～3下，基金结余量在2035年为负值。在方案4和5下，基金结余量在2035年为正值，且在方案4下，基金结余量曲线处于缓慢下降阶段，同时考虑到基金的可持续性及基金的收支原则，此时方案4最优。

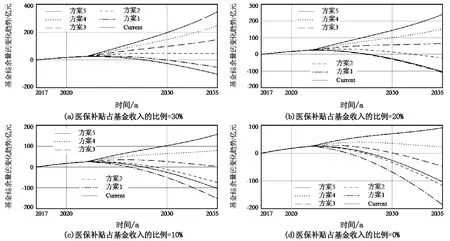
图8 职工缴费率和单位缴费率变动下基金结余量变动趋势预测

综上，对职工缴费率和单位缴费率及医保补贴占基金收入的比例的综合调控可知，当职工缴费率和单位缴费率为0.22%时，长期护理保险能实现独立且可持续的运行。

5 结论与对策建议

以长期护理保险筹资费率水平为研究对象，分析长期护理保险筹资系统，构建长期护理保险筹资系统动力学模型，考察不同要素参数变化对长期护理保险基金结余量的影响。在此基础上，以江西省上饶市为例进行实证分析，设计综合调控方案，模拟预测长期护理保险基金结余量的变化。结果显示，随着老龄化水平的提升，失能老人数量持续递增会使上饶市长期护理保险基金难以持续发展，同时过度依赖于医保基金不利于长期护理保险基金的独立运行。根据上述结论，提出以下对策建议：

(1)完善老年健康支撑体系。针对健康老人，由卫生部门为老年人组织失能预防干预培训，提高老年人健康素养和健康水平，从源头上减少老年人失能的发生。针对失能老人，政府应根据失能评估结果，为失能老人提供不同的支持，以达到延缓失能的目的。其中对于轻度失能老人，重点是通过加强生活防护延缓失能。对于中度失能老人，重点是定期开展康复训练延缓失能。对于重度失能老人，重点是发展医院、护理院等机构照料，为其提供标准化照料服务延缓失能。

(2)建立互助共济、责任共担的多渠道筹资机制。构建以个人、单位、政府为主，医保、福彩、社会捐赠等为辅的多渠道筹资机制，要通过拓宽筹资渠道的方式减轻筹资机制的压力。积极探索社会捐赠、福利彩票划转等筹资渠道，充分调动个人、社会及社会团体参与筹资的积极性，拓宽社会化筹资渠道。同时要注重长期护理保险运行的独立性，可以通过逐步提高职工缴费率及单位缴费率的方式，降低对医保基金的依赖性。