一种快速的属性与属性值合一数据约简算法

关素洁，段卓镭，赖观祥，黎 敏，邓少波

(南昌工程学院 信息工程学院，江西 南昌 330099)

Rough集理论是由20世纪80年代波兰人Z.Pawlak提出的一种新的数学工具，它通过严格的数学公式来处理不精确、不确定的问题，具有演绎、归纳和常识推理等能力。Rough集理论在机器学习、知识获取、决策分析、数据库知识发现、专家系统和模式识别等方面得到了广泛的应用[1-10]。当今Rough集理论已经从粒及其粒计算角度发展到多粒度，三支决策等研究领域，并且在人工智能、大数据知识表示与推理等研究领域得到广泛应用。

相较于传统粗糙集，多粒度粗糙集基于多粒度思想，在处理复杂现实问题时进行多层次、多角度和深层次地分析，展示出了优异的效果。陈静雯[11]等从多粒度、多层次的角度，结合邻域多粒度粗糙集与粒计算模型，设计了基于最大粒的悲观邻域多粒度粗糙集规则获取算法。徐怡[12]等从知识粒度的权重分布分析，提出了基于权重分布的多粒度粗糙集模型。林梦雅[13]等将改进的量化容差关系和多粒度粗糙集模型相结合，提出一种基于量化容差关系的多粒度粗糙集模型。胡善终[14]等给出了决策类下近似布尔矩阵的定义，基于此提出了多粒度粗糙集粒度约简的高效算法。

三支决策理论通过“三分而治”的思想对传统的“非黑即白”的二支决策进行了改进。徐健锋[15]等人从度量驱动的角度进一步研究三支决策的论域问题；薛占熬[16]等人基于三支决策模型，结合直觉模糊集，将基于直觉模糊集的三支决策模型扩展为一般模型；张春英[17]等将集对信息粒空间的结构划分为正同域、负反域和差异域，提出基于集对信息粒空间的三支决策模型；岳文琦[18]等在混合决策系统中提出模糊效用三支决策模型，并在此基础上提出正域分布保持和最大效用启发式属性约简算法。

在当今大数据时代中，数据的价值日益凸显。但海量、高维的数据和不相关、冗余的属性和属性值都给数据存储和知识获取带来了巨大的难度。Rough 集理论数据约简分为两部分：属性约简与属性值约简。属性约简又被称为特征选择，是机器学习和数据挖掘中一个十分重要的数据预处理方法。属性约简要求尽可能多地删除冗余属性而且要求约简后的属性能维持原有的知识，这是个NP难问题[19]。属性值约简是为了消除冗余，其约简过程复杂，需要对每一条决策规则中的每个属性进行判断[20-25]。

当今大多数研究者对决策表进行属性约简，主要是为了提高效率，降低复杂度。何明[26]等从信息论的角度来描述属性重要度，并设计了时间复杂度为O(|A|2|U|2)的属性约简启发式算法；刘少辉[19]等提出了一种基于正区域的属性约简算法，并设计了一个启发函数，通过快速排序的方法将属性约简算法的时间复杂度降为O(|C|2|U|log |U|)；Fan[27]等提出了最大决策邻域粗糙集模型，并基于该模型设计了一种属性约简算法，其时间复杂度为O(|A|2|U|2|U/D|)；徐章艳[28]等设计了一个量度属性重要性的计算公式，并以此作为属性约简的启发函数，提出了一个时间复杂度为max[O(|C||U|)，O(|C|2|U/C|)]；胡峰[29]等对二维表快速排序的复杂度进行了详细分析与探讨，利用快速排序方法进行细分；邓少波[30]等提出了一种属性与属性值合一的约简方法，但其算法的时间复杂度比较高，需要进一步改进。本文受文献[28]的启发，针对当前问题，提出了一种快速属性与属性值合一的约简算法，使得属性与属性值合一约简算法时间复杂度降为O(|C|2|U|)，提高约简效率，降低了约简时间。本文主要贡献是：提出一种线性时间复杂度的属性与属性值合一约简算法，其线性时间复杂度是本文提出的算法优势。

1 基础概念

在决策表中，数据约简分为两步：一是属性约简，等价于从决策表中约去一些不必要的列；二是属性值约简，等价于从决策表每一行中约去一些不必要的属性值[1-4]。下面给出一些相关理论知识。

定义1设有决策表S=(U，A，C，D，V，f)，其中U是个体集合，U={u1，u2，…，un}。C是非空条件属性集合，D是非空决策属性的集合，A是决策表的属性，且C∩D=∅，C∪D=A。V=∪Va，∀a∈A，Va是属性a的值域。f：U×A→A，f是一个信息函数，表示任意个体的每一个属性都有对应的属性值。设∀a∈A，u∈U，则有f(u，a)∈Va，二元不可区分关系INP(P)定义如下：

INP(P)={(x，y)∈U×U|∀a∈A，P⊆A，f(x，a)=f(y，a)}

U/IND(P)构成关系INP(P)的一个划分，简记为：U/P；U/P={[x]p|x∈U}，其中[x]p是等价类，定义如下所示：

[x]p={y|∀a∈P，且f(x，a)=f(y，a)，且∀x，y∈U}。

定义2对于一个决策表T=(U，A，C，D)，如果对于任一个体y≠x，dx|C=dy|C→dx|D=dy|D，则称dx规则是一致的，否则dx是不一致的[1-4，19]。

定义3如果决策表中所有的决策规则都是一致的，则该决策表T=(U，A，C，D)是一致的；否则该决策表是非一致的[1]。

由定义2和定义3可知，在信息系统的决策表中，一致性决策规则说明条件属性值相同蕴含着决策值必须相同，即是决策值函数依赖于条件属性值。因此，具有相同的条件属性值是不能对应不同的决策值，而相同的决策值却可以依赖于多个不同的条件属性值，这样才能保证决策规则的一致性以及决策表的一致性。

命题1对于一个决策表T=(U，A，C，D)，将属性集A中的属性逐个移去，每移去一个属性即刻检查其决策表，如果不出现新的不一致，则该属性是可以被约去的；否则该属性是不能被约去的，称这种方法为属性约简数据分析方法[1-4]。

命题2设φ→ψ是决策表上的一条决策规则，a为条件属性，v是属性a所映射的属性值，属性值v可被约去当且仅当：|-(φ→ψ)→((φ-{(a，v)}→ψ)，其中φ和ψ均为决策表上的Rough逻辑公式[1-4]。

该命题揭示了决策规则的条件属性值可以被约去当且仅当约去之后还能保持此规则的一致性[1，31，33]。

命题1和命题2是决策表的属性约简与属性值约简准则。

推理1在决策表S=(U，C，D，V，f)中，∀Q⊆P⊆(C∪D)，则有U/P≤U/Q[28]。

由推理1可知，U/(C∪D)≤U/C，也就是说，求U/(C∪D)是在U/C基础上再次细分。

推理2设有决策表S=(U，C，D，V，f)，P⊆(C∪D)，∀c∈P。U/P是在U/{c}等价类族基础上进行了n-1次细分，其中P={c1，c2，…，cn}，n=|P|。

证明当n=1时，也就是|P|=1时，有P={c，c∈(C∪D)}，显然，U/P对/{c}进行了|P|-1=0次细分。因此，n=1时命题成立。

假设n=k时(也就是|P|=k时候)命题成立。即U/P是在/{c}等价类族基础上进行了k-1次细分命题成立，其中P={c1，c2，…，ck}，U/P={E1，E2，…，Em}，m是正整数且m≤|U|，U=E1∪E2∪…∪Em，k=1，2，…，n。

那么当n=k+1时，令P′=∪{Ck+1}，|P′|=k+1，由定义1得到：U/P′中的任意元素[x]P′=y|f(x，Ck=1)=|f(y，Ck=1)；x≠y，且∀E∈U/P，∀x，y∈E。即对U/P中每一个等价类，以Ck=1属性求细分后得到的等价类族。

可知，U/P′在U/P等价类族基础上进行了1次细分，那么/P′是在U/c等价类族基础上进行了k次细分，所以n=k+1时命题成立。

得证。

由推理2可知，在求多个属性的等价类族时，可以在单个属性的等价类族中，对其每个等价类依次根据其他属性的属性值进行多次细分，从而得到具有多个属性的等价类族。

推理3给定任意决策表S=(U，C，D，V，f)。每去掉一个c后令C′=C-c，U/C′={E1，E2，…，Em}。对于∀Ei∈U/C′，设经过|D|次细分后等价类Ei被细分为：Ei1，Ei2，…，Eipi个等价类；则U/(C′∪D)={E11，E12，…，E1p1；E21，E22，…，E2p2；…；Em1，Em2，…，Empm}，很明显U/(C′∪D)是对U/C′中所有等价类进行|D|次细分的结果，其中pi≤|Ei|，Ei=Ei1∪Ei2∪…∪Eipi，∀c∈C，m≤|U|，U=E1∪E2∪…∪Em，i=1，2，…，m。

如果pi≥2，那么Ei中的个体在c属性上所映射的属性值即为核值。

证明已知每去掉一个c后令C′=C-c，U/C′=E1，E2，…，Em。对于∀Ei∈U/C′，设经过|D|次细分后等价类Ei被细分为：Ei1，Ei2，…，Eipi个等价类；

则有：U/(C′∪D)={E11，E12，…，E1p1；E21，E22，…，E2p2；…；Em1，Em2，…，Empm}，其中pi≤|Ei|，

Ei=Ei1∪Ei2∪…∪Eipi，∀c∈C，m≤|U|，U=E1∪E2∪…∪Em，i=1，2，…，m，也就是说U/(C′∪D)是对U/C′等价类族中每一个等价类进行了|D|次细分。

发挥代建规模和品牌优势.城投公司代建的优势已经形成.城投公司是政府唯一指定的国有企业，是富有实力的专业团队，对政府性资产有较强运作能力；善于进行投资优化，不超概算；管理成本低，并且在廉政建设和安全生产方面都有切实保证.

如果pi≥2，那么在决策属性集D上，U/C′中某个等价类经过|D|次细分后分为至少两个新等价类，则有：∀x∈Ei，∃y∈Eik∧x∈Eij∧x≠y，其中k，j=1，2，…，pi，k≠j。

于是∀x∈Ei，∃y∈Eik，Eik⊆Ei，可知，x，y∈Ei，也就是dx|C=dy|C。

那么由(∃y∈Eik)∧(x∈Eij)，可知，dx|D≠dy|D。

由约简数据分析方法[1-4]可知：c属性是不可以被约简的，且∀x∈Ei个体x在属性c上所映射的属性值即为核值。得证。

推理3表明如果在决策属性D上U/C′中某个等价类经过|D|次细分后分为至少两个新的等价类，那么在属性集D上所映射的属性值即为核值。

2 快速U/P算法

Rough集理论中，不可区分关系表明个体之间的性质，是一种二元关系。利用不可区分关系，可以得到或推理出Rough集理论中其他的性质与定理，由不可区分关系可以得到相应的等价类族。文献[19]利用快速排序的方法给出了一个求INP(P)的等价类族算法，其时间复杂度为：O(|C|2|U|log |U|)；文献[28]利用决策表中属性值的规律，以基数排序的方法给出了一个计算INP(P)的等价类族算法，其时间复杂度为：max(O(|C||U|)，O(|C|2|U/C|))。本文受文献[28]算法的启发，考虑决策表中属性值的规律，利用分而治之思想，对每个等价类进行细分，给出了一个新的求INP(P)算法，其时间复杂度为O(|P||U|)。

算法1：equivalence_classes(U，P)，求U/P。

input：决策表S=(U，C，D，V，f)，P⊆C，m=|C|；

Step1：求每一个属性ci的最大属性值与最小属性值，并以数组C_max[i]、C_min[i]存储；

Step2：c1∈P且令C′={c1}，根据个体uj的属性值来决定该个体属于哪个等价类，得到链表U′；

Step3：由上一步得到的链表为U′，令P′={c2，c3，…，cm}，∀ck∈P′，求U/C′等价类族。该步骤为两层循环嵌套，外循环需要遍历剩余的其他属性，令C′=C′∪{ck}，每一次增加一个剩余属性，内循环为计算U/C′等价类族。

本文求U/P，是在求U/{c}的基础上进行了|P|-1次细分，细分时，根据上一次细分的结果，对每个等价类以新添加的一个属性的属性值作为依据进行细分。

3 合一约简算法

属性约简是约去冗余的属性，而属性值约简则是约去冗余。本文利用算法1求U/P约简算法思想，提出一种快速的属性与属性值合一约简方法。该方法约简时属性与属性值约简同时进行。

命题3如果一个属性可以被约去，那么它的所有属性值都不是核值。

证明可采用反证法证明，证略。

算法2：约简算法，reduce(U，C，D)：

input：决策表S=(U，C，D，V，f)；

output：核值表；

Step1：每去掉一个属性c，c∈C，令C′=C-c，求/C′等价类族，U_C′=equivalence_classes(U，C′)；

Step2：已知，U_C′，D={d1，d2，…，dr}，求U/(C′∪D)，U_D=equivalence_classes(U_C′，D)；

Step3：设U_C′链表中当前节点的数据域为x，U_D链表中当前节点的数据域为y。同时遍历这两个链表，如果x不为0并且y为0，那么U_C′当前等价类中个体在属性c上所映射的属性值即为核值，并使U_D中当前节点指向下一个节点，否则U_C′和U_D中的当前节点都移向下一个节点；

Step4：重复Step1～3的操作，直到属性集C中的每个属性都被判断过，由此得到的属性集合C″；

Step5：令C=C″，重复执行Step1～4步。并输出决策表的核值表。

此算法是以推理3、命题3为理论基础，约简过程中，属性约简与属性值约简是同时进行的。

4 示例分析

现以文献[1]第63页的例子为例，描述下本文的约简方法。已知决策表T=(U，A，C，D)，其中C={a，b，c，d}，D={e}(如表1所示)。该决策表约简过程如下所示：

4.1 求U/P实例

令C′={b，c，d}，求U/C′，调用equivalence_classes(U，C′)函数，执行过程如下：

在下面演示过程中，每个链表的起始部分为头指针，链表最后的部分为尾指针，其数据域为0。在演示过程中，并没有把尾指针的数据域描述出来。

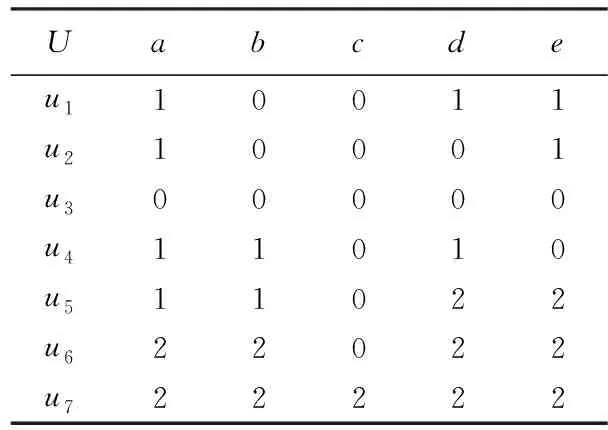
表1 决策表

Step1：求C′中各个属性的最大与最小属性。属性b：C_max[1]=2，C_min[1]=0；属性c：C_max[2]=2，C_min[2]=0；属性d：C_max[3]=2，C_min[3]=0；

Step2：求U/c1，得到新的链表U′→u1→u2→u3→0→u4→u5→0→u6→u7←U′_rear；

Step3：第1次外循环：在U/b基础上，求U/(b∪c)的等价类族。执行内循环得到：U_middle→u1→u2→u3→0→u4→u5→0→u6→0→u7←U_middle_rear与U′→u1→u2→u3→0→u4→u5→0→u6→0→u7←U′_rear。第2次外循环：在U/(b∪c)基础上，求U/(b∪c∪d)。执行内循环得到：U_middle→u1→0→u2→u3→0→u4→0→u5→0→u6→0→u7←U_middle_rear与U′→u1→0→u2→u3→0→u4→0→u5→0→u6→0→u7←U′_rear。输出：U_C′→u1→0→u2→u3→0→u4→0→u5→0→u6→0→u7←U_C′_rear；

equivalence_classes(U，C′)执行结束。

4.2 合一约简算法示例

已知C={a，b，c，d}，D={e}，U={u1，u2，u3，u4，u5，u6，u7}，调用reduce(U，C，D)执行过程如下：

Step1：去掉属性a，令C′={b，c，d}，U_C′=equivalence_classes(U，C′)，得到：U_C′→u1→0→u2→u3→0→u4→0→u5→0→u6→0→u7←U_C′_rear；

Step2：U_D=equivalence_classes(U_C′，D)，得到：U_D→u1→0→u2→0→u3→0→u4→0→u5→0→u6→0→u7←U_D_rear；

Step3：U_C′中的等价类{u2，u3}被细分为两个等价类{u2}{u3}，那么个体u2、u3在属性a上所映射的属性值即为核值，属性a不可被约简；

Step4：令C′={a，c，d}，继续执行Step1～3，等价类{u1，u4}被细分为{u1}{u4}，个体u1、u4在属性b上所映射的属性值即为核值；

令C′={a，b，d}，继续执行Step1～3，U_C′中每个等价类没有被细分，属性c上没有核值，可以被约去；

令C′={a，b，c}，继续执行Step1～3，等价类{u4，u5}被细分为{u4}{u5}，个体u4、u5在属性d上所映射的属性值即为核值；

Step5：由Step4可知，属性c是可以被约去的，并得到部分核值，令C″={a，b，d}，D={e}继续执行Step1～4，得到所有核值，结果如表2所示。

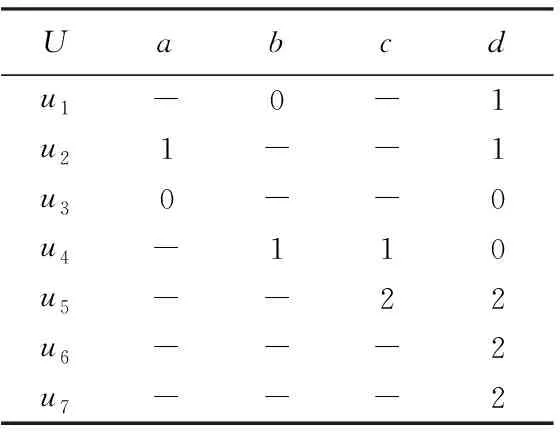
表2 决策表的核值表

(表2中的“-”为空值，表示可被约去的属性值，其它则表示为核属性值)

5 约简算法分析

在诸多属性约简方法中，求U/P等价类族算法效率影响到属性约简方法效率，如何在更快更短时间内完成属性约简与属性值约简全过程，是诸多学者一直都在致力解决的问题。本文提出一种新的求U/P方法，并以此作为本文约简方法的基础，使得属性与属性值合一约简算法时间复杂度降为O(|C|2|U|)。其算法复杂度分析分别如下：

5.1 U/P时间复杂度分析

本文算法1是求U/P的算法，算法1各个步骤的时间复杂度分析如下：

Step1：求|P|个属性的最大属性值与最小属性值，其时间复杂度为O(|P||U|)；

Step2：主要是对|U|个个体根据其属性值来确定个体所在的等价类，易知其时间复杂度为O(|U|)；

Step3：是利用双重循环控制，内循环是遍历U′中的每个等价类，其时间复杂度为O(|U|)，外循环是重复内循环的操作，重复|P|-1次操作。可知，整个Step3的其时间复杂度为：O((|P|-1)|U|)；

因此，求U/P算法的整个时间复杂度为O(|P||U|)。但该算法需要额外的空间存储C_max、C_min、middle、U_middle等中间结果，不难分析，本文算法1的空间复杂度为O(|C||A||U|)。

5.2 属性与属性值约简复杂度分析

本文算法2是属性与属性值合一约简算法，算法2时间复杂度分析如下：

Step1：求U/C′等价类族，由上分析可知，其时间复杂度为O(|C||U|)；

Step2：求U/(C′∪D)等价类族，由上分析可知，其时间复杂度为O(|D||U|)；

Step3：主要是遍历U_C′链表，其时间复杂度为O(|U|)；

Step4：重复Step1～2的操作，重复|C|次，一般|D|<|C|，因此总的时间复杂度为O(|C|2|U|)；

Step5：根据Step4得到属性集合C″，重复Step1～4的操作，可知，Step5的时间复杂度为O(|C″|2|U|)。而|C″|≤||，所以，Step5的时间复杂度为O(|C|2|U|)。

由于Step5与Step1～4是分开执行的，因此整个算法2的时间复杂度为O(|C|2|U|)。算法2需要存储U_C′，U_D等链表，并要保存决策表的核值表，可知，算法2空间复杂度为O(|A||U|)。

5.3 与其他算法比较

文献[30]是一种属性与属性值合一约简方法，其时间复杂度为O(|A||U|2)，该算法融合了属性与属性值约简全过程，通过扫描依次决策表，求出所有属性的等价类族，然后对这些等价类族进行取交集的运算，其效率有待提高。

本文提出了求U/P等价类族的快速方法。该算法根据个体的属性值确定个体所在的等价类，对等价类族中的每个等价类进行细分，把个体集合搜索范围缩小到某个等价类中，从而减少搜索空间和搜索时间，提高了算法的效率，并以此作为本文算法的核心，进行属性与属性值合一约简，其时间复杂度为O(|C|2|U|)。

5.4 进一步分析说明

本文算法受文献[28]的启发，如果决策表中每个属性的属性值是有序的、相邻的整数，则可以根据个体的属性值来决定个体位于哪个等价类中。如果决策表中各个属性的属性值不是有序的、相邻的整数，例如某属性的属性值有2、10、100等属性值，则需要对之进行替换，变成1、2、3等属性值，即是一对一地替换成有序的、相邻的整型属性值。

文献[28]并没有考虑属性值不是有序的、相邻的整数这种情况，例如某属性的属性值有2、10、100等属性值，则该算法至少需要分配100个相应的内存空间来处理，而本文只需要分配3个相应的内存空间。

在对决策表进行数据替换时，应该遵守如下规则：

(1)任意等价类所包含的个体元素不会发生改变；

(2)替换前各属性的属性值与替换后的属性值是一一对应的；

(3)替换后的各个属性的属性值应该是有序的、相邻的整型属性值。

6 仿真实验

6.1 U/P仿真实验

仿真实验主要目的是验证本文提出的算法是线性的时间复杂度，通过大量的仿真实验来验证算法的有效性。仿真实验中使用数据集选择的是UCI机器学习数据库(https：//archive.ics.uci.edu/ml/index.php)中的6个数据集，实验所用的数据集描述如表3所示。在实验中程序代码的环境是Python3.7。仿真实验硬件配置为：内存为8.0 GB，CPU为Inter(R)Core(TM)i7-5500U CPU @ 2.40GHz 2.40GHz。在仿真实验的过程中，按比例随机选取数据集中的数据作为数据子集，同时将10次运行时间的平均值作为最终实验结果，使实验结果更加稳定。

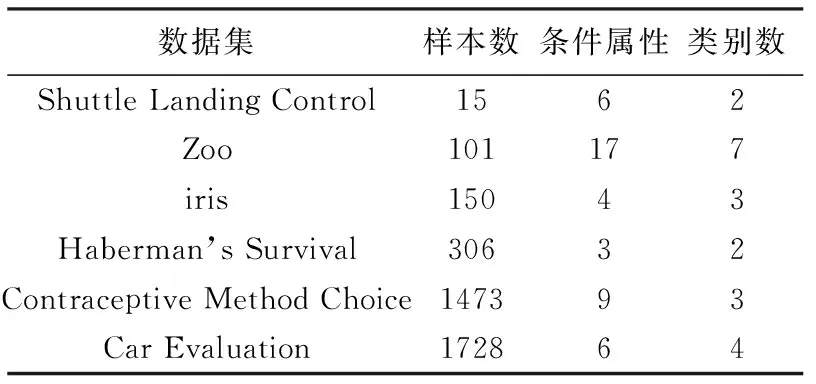
表3 UCI实验数据集

在实验前需要对数据进行预处理操作。首先使用Weka软件中的离散化功能对连续型数据进行了离散化处理，数据离散化处理完成后再进行替换处理，使得替换后的每个属性的属性值是有序、相邻的整数。实验时，本文随机选择了数据集总样本数的10%，20%，30%，40%，50%，60%，70%，80%，90%，100%作为数据子集分别测试本文算法1的时间特性，实验结果如图1的6个子图所示，其中横轴表示数据子集的样本数与总样本数的比值，纵轴表示算法计算所消耗的时间。

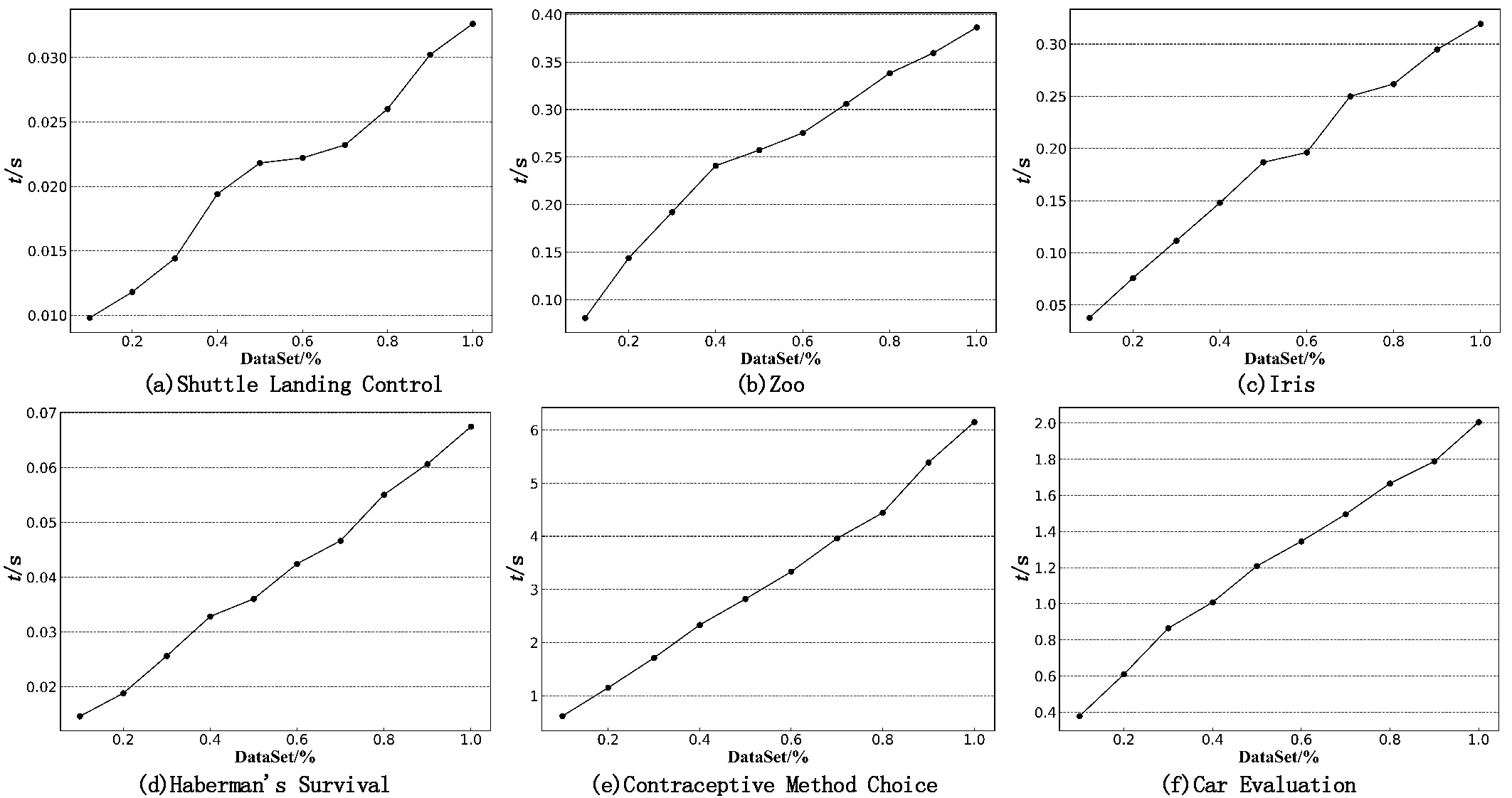
图1 U/P算法计算时间结果

通过图1可以看出，在Shuttle Landing Control、Zoo和Iris数据集上所得到的计算时间结果曲线并不平稳。由于这3个数据集的样本数较少，并且数据子集是通过随机挑选出来的，这都带来了很大的不稳定性。虽然前3个数据集的计算时间结果不是太稳定，但是其结果曲线基本是直线。对于样本数较多的Haberman’s Survival、Contraceptive Method Choice和Car Evaluation这3个数据集，其计算时间结果曲线较为平稳，几乎都是直线。通过6组实验仿真结果可以得出，对以上6个数据集使用U/P算法，其计算时间结果线条符合本文求U/P算法的时间复杂度特性。

6.2 属性与属性值合一约简算法仿真实验

为了进一步测试本文所提出的属性与属性值合一约简算法时间特性，依然选取上述预处理完成的6个数据集来进行实验测试。其结果如图2所示。

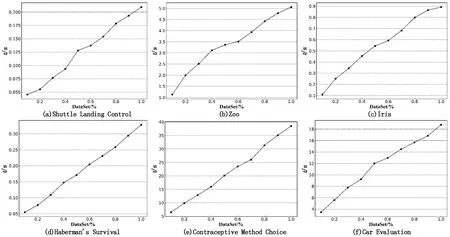
图2 属性与属性值合一约简算法计算时间结果

从仿真实验图2可以看出，这些使用属性与属性值合一约简算法的计算时间结果曲线的线性特征和U/P算法的基本一致，这些线条几乎是一条直线，符合本文算法2的时间复杂度为线性的特征。

本文仿真实验主要目的是验证本文提出的算法时间复杂度是线性的。其后续工作将进一步开展本文算法的分类准确率与约简效率等研究内容。

7 结束语

本文利用属性值有序、相邻的特性，设计了一个求U/P的快速方法。并以此作为本文属性与属性值合一约简算法的基础，提出了一个时间复杂度为O(|C|2|U|)的约简算法。并利用了多个UCI数据集验证了算法的时间复杂度。本文研究重点在于提出一种线性时间复杂度的属性与属性值合一约简算法，其线性时间复杂度是本文的主要特点。