初中数学动点问题解决策略研究
吴丽蓉
(福建省漳州市第三中学 363000)
1 初中数学动点问题概述
动点问题又被称之为“几何动态”题目,通常是指在一个几何图形中,存在某一个动点,这些动点可以沿着特定的方向,或者在特定的范围内进行移动.在此基础上,结合动点的运动特点,对几何图形的变化规律展开探究.与其他的题目类型相比,动点问题更具有综合性,是对基础知识的升华.学生在进行解答的过程中,常常需要包揽所有的数学知识点,要具备很高的知识掌握水平、数学理解能力、知识迁移和应用能力等.可以说,动点问题具备一定的选拔性,在中考等选拔性考试中尤为常见.
2 初中数学动点问题解决策略研究
2.1 单动点问题解决策略
单动点数学问题,顾名思义就是只有一个运动的点.通常,这一类题目常常出现在“平行四边形性质和判定、特殊三角形的性质和判定、勾股定理、函数图像”等知识点的综合考查中.在对这一类动点问题进行解决的过程中,对其进行分析和转化,找出具体的解题思路,是唯一的方法.
2.1.1 点在直线上运动
例1如图1所示:牧马人从A地出发,走到一条笔直的河边l饮马,然后到B地,牧马人找到河边的什么地方饮马?可使得其所走的路程最短?
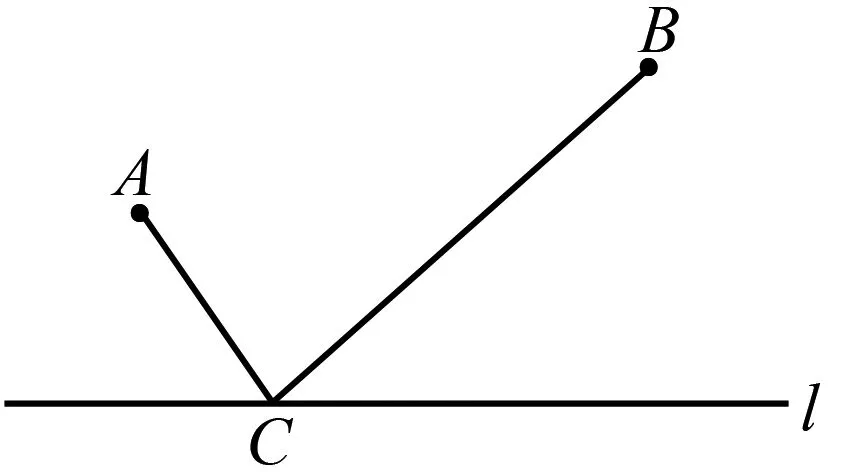
图1
这一道数学题目,实际上就是考查了“点在直线上运动”,即在直线l上确定点C,使得其满足题意.学生在对其进行解答的时候,可先作出点B关于直线l的对称点B′,连接AB′,线段AB′与直线l的交点C即为所求.可以说,这一道数学题目就是典型的单动点问题,运用到的基本数学思路是:利用对称,把直线同侧两点转化为在直线两侧的两点.两个定点分别在已知直线的两侧,如何在直线上求一个动点,使其达到这两个点的距离最短.
2.1.2 点在数轴上运动
数轴是初中数学中最为重要一个部分内容,也是一种特殊的工具.将几何和代数结合起来,动点在数轴上的运用也比较常见,不仅是学生学习的重难点,也是发展学生数形结合思想的关键.例如,在数轴上有三个点,分别为A、B、C,其中点A表示的数为1,点B表示的数为-5.点C为数轴上的动点.如果C到A的距离等于2倍的C到B的距离,求C表示的数?
在这一题目解答的过程中,学生需要运用到分类讨论的思想,先结合题目中给出来的已知条件,设C表示的点为X,并从题目中得出AC=2BC.之后,开展分类讨论,得出最终的正确答案.在对这一类数学题目进行解答的时候,分类讨论是关键,必须要明确不同的情况,并围绕其展开讨论,最终得到相应的解决方案.
2.1.3 等角形问题
在初中数学学习中,等角形问题主要是动点与角有关的问题.通常情况下,在这一类型的数学题目中,常常要求学生在给出来的数学图形上,或者某一个区域中确定一个或者几个以动点作为定点的角,使其于已知的角相等.例如:如图2所示,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中,A(1,0)、B(4,0);与y轴相交于点C(0,2),连接AC、BC.求:抛物线的解析式;如果点P在抛物线的对称轴上运动,要使∠CPB=∠CAB,求P点的坐标.
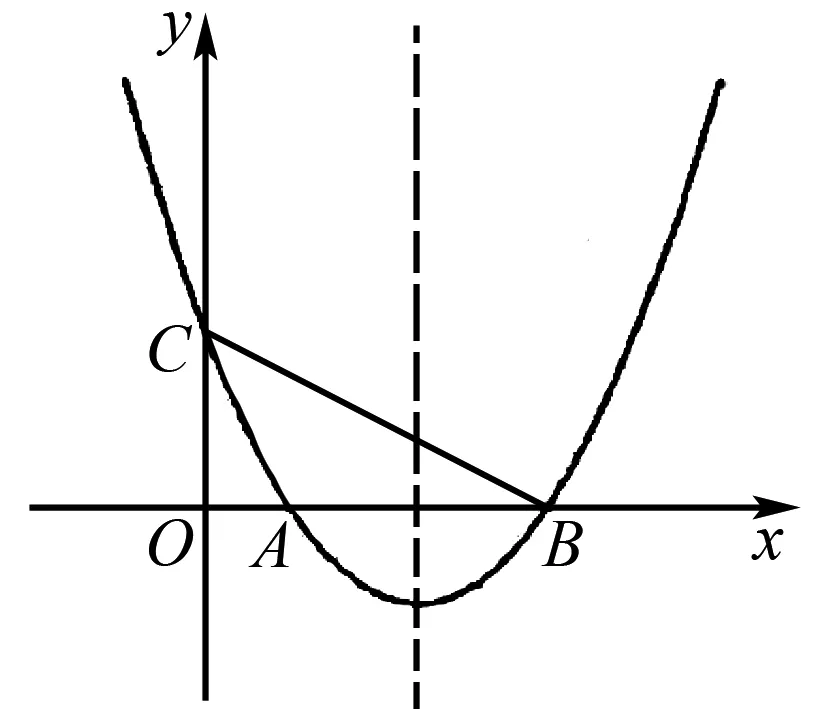
图2
这就是一道十分典型的等角形问题,在对这一题目解决的过程中,我们常常需要借助待定系数法,由问题中给出的条件∠CPB=∠CAB,可知角的两边都要经过B、C两点,进而逐渐联想到“同弧所对的圆周角相等”这一数学定律,并由此想到:只要将△ABC的外接圆做出来,使其与对称轴相交于两个点.之后,学生就可轻松利用第一问的解析式,采用分类讨论的方式,围绕当点P位于BC下方、当点P位于BC上方的时候,分别进行讨论,并做出相应地解答.
2.1.4 动点与三角形相关的问题
在初中数学考试中,关于“动点和三角形相结合”的考查最为常见,主要包括:动点和特殊三角形、动点与三角形面积、动点与三角形周长、动点与相似三角形等.例如,已知线段AB,在平面上取一点P,使△PAB为直角三角形.这一数学题目就考查了构建直角,即动点与特殊三角形这一问题.在这一数学题目中,涉及到的基本原理主要包括两个方面,即:如果线段AB为斜边,那么点P必定在以AB为直径的圆上;如果线段AB为直角边,以点A为直角的顶点,则点P必然在过点A的AB垂线上;如果线段AB为直角边,以点B为直角的顶点,则点P必然在过点B的AB垂线上;在这一道数学题目中,由于直角的位置不确定,学生必须要结合基本的定理,通过具体问题具体分析,结合不同的情况,运用不同的知识点进行求解.
2.1.5 动点与四边形有关的问题
在初中数学教学中,动点与四边形相关的问题也比较常见,主要体现在:面积最值问题、周长最值问题、构造特殊四边形等问题.例如:如图3所示,已知抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过点A(-1,0)、B(5,-6)、C(6,0),求抛物线的解析式;在直线AB下方的抛物线上是否存在一点P,使得四边形PACB的面积最大?如果存在,求出点P的坐标;若不存在,说明理由.

图3
学生在对这一数学题目进行分析的时候,可借助抛物线交点式,以及待定系数法进行解析;在对第二问进行求解的时候,可将平行四边形面积进行转化,使其成为求解三角形面积问题.在进行转化的过程中,可指导学生分析题意,确定出△ABC面积,学生只需要将△ABP面积确定出来即可.由于这一道数学题目中,要想求出四边形面积最大的动点坐标,可将其转化为求△ABP面积最大时候的动点坐标.随即,借助“切割法”的原理,学生只需要将切割线最大时的动点坐标确定出来即可.
2.2 双动点问题解决策略
与单动点问题相比,双动点问题难度比较大,对学生的数学基础知识、思维、综合能力要求相对较高.结合“双动点”数学问题的内涵,在对其进行解答的时候,常常可通过四步进行,即:一判、二找、三分类、四计算.首先,判断题目的类型,分析其属于单动点还是双动点的数学问题,明确题目中要求的数学问题是特殊的图形,还是周长和面积等;其次,对题目进行分析,找出题目中给出的不变因素,以减少解题时候的分类讨论情况,使得复杂的数学问题变得更加简单、明了;再次,结合数学题目中的不变量、不变形进行作图分析,再结合题目中所求的数学问题,展开分类讨论;最后,利用所学的数学基础知识,根据图形中的几何特征,展开解题计算.
鉴于双动点数学问题的内涵,在对其进行解答的时候,常常要运用一定的化归思想,将题目中的双动点、多个动点进行转化,使其成为单动点的数学问题.并且还要充分利用题目中的“不变性、不变量”进行转化,旨在减少变量的效果;另外,鉴于数学双动点考查的数学题目,常常要结合数学题目展开分类讨论.在展开分类讨论的时候,基本上都是结合题目中的“不变量”、“不变性”展开的.学生只要具备扎实的数学基础知识、基本技能,即可在有效的分类讨论中,完成双动点数学问题的解答.


图4
这是一道典型的双动点数学问题,以三角形作为背景,题目中存在一个定点C,其余的两点M、N均为动点.在对这一数学问题进行解决的时候,基本上都是遵循“化归思想”,按照上述的步骤,利用“对称性”的原则,将定点进行转化,并得出“垂直线段最短”这一结论,进而解决所求的问题.
综上所述,在初中数学题目中,动点问题尤为常见,且学生的失分率比较高.同时,动点问题不仅考查了学生的数学基础知识,也融入了大量的数学核心素养.因此,初中数学教师在安排课堂教学时,不仅要关注数学动点问题,还应结合不同的动点问题,采取最佳的教学策略,引导学生在学习中,总结出数学动点问题的一般解题思路.

