高速列车排障器底部后端扰流对转向架区域流场与气动噪声特性的影响

朱剑月，程冠达，陈 力，高 阳，张 清

（1.同济大学 铁道与城市轨道交通研究院，上海 201804；2.同济大学 汽车学院，上海 201804；3.大功率交流传动电力机车系统集成国家重点实验室，湖南 株洲 412001；4.大连交通大学 机械工程学院，辽宁 大连 116028；5.中车长春轨道客车股份有限公司 国家轨道客车工程研发中心，吉林 长春 130062）

当高速列车运行速度超过300 km·h-1并且不断提高时，气动噪声将高于滚动噪声和牵引噪声，从而成为主要噪声源［1-3］。

高速列车转向架区域气动噪声的研究多数采用现场实测和风洞试验。杨妍等［4］现场实测了300 km·h-1速度下高速列车通过桥梁和路堤段线路时噪声源特性，发现与通过桥梁段时相比列车通过路堤段时车身和受电弓区域产生的气动噪声较大，而转向架区域噪声略低。王东镇等［5］进行高速列车350 km·h-1速度通过时声源识别测试，表明高速列车气动噪声源主要位于转向架和受电弓区域；列车上不同部位转向架产生气动噪声的幅值和频谱特性不同；车头部位转向架由于受到来流冲击作用，辐射的气动噪声较其他转向架强。Mellet 等［6］基于现场测试获得了TGV（Train à Grande Vitesse）Duplex 高速列车300 km·h-1速度通过时的噪声云图，发现车头转向架区域为主要噪声源。Kurita等［7］对新干线高速列车进行了在线测试，通过在转向架舱外侧安装裙板和转向架舱内壁敷设吸声材料，有效降低了高速列车转向架区域气动噪声的形成与辐射。郝南松［8］基于航空声学风洞，对高速列车1∶8 缩比模型进行了气动噪声测试，结果表明列车主要气动噪声源低频段位于车头转向架区域、高频段位于受电弓区域；由于转向架数量较多，转向架区域气动噪声贡献量高于受电弓区域。Lauterbach 等［9］根据ICE3（InterCity Express）高速列车1∶25 缩比模型，在声学风洞里采用传声器阵列进行转向架区域气动噪声源识别，比较分析不同措施的降噪效果。Latorre 等［10］基于低噪声风洞，对1∶7 缩比的高速列车模型进行气动噪声测试，发现转向架区域产生了宽频特性的气动噪声，转向架结构中直接受到来流冲击作用部件产生的气动噪声较大。

随着计算能力的提高，数值仿真方法被应用于高速列车整车和各关键部位的气动噪声特性分析。高阳等［11］根据声类比方法和声扰动方程计算分析高速列车比例模型流场以及近场和远场气动噪声特性，声学风洞试验结果验证了远场气动噪声预测的准确性。张军等［12］通过建立高速列车气动噪声数值模拟模型，计算分析列车外部稳态和瞬态流场以及远场气动噪声，结果表明头车车体、一位转向架和受电弓部位是高速列车远场辐射噪声的主要噪声源，高速列车不同气动噪声源满足声源叠加原理。谭晓明等［13］采用无限长隧道内高速列车气动噪声计算模型，比较分析高速列车在明线上与隧道内运行时流场与气动噪声源特性，认为与明线上运行相比高速列车在隧道内运行时流场结构尺度与强度、气动噪声源强度均较大，隧道活塞效应使得峰值频率周围较窄范围内等效声源声功率显著增加。Zhu等［14］基于数值模拟方法，计算分析高速列车3 车编组缩比模型气动力和远场气动噪声特性，表明列车气动噪声为偶极子噪声源并发现车头转向架区域辐射了较强的气动噪声。黄莎等［15］模拟计算高速列车车厢连接部位由于流体相互作用诱发的气动噪声，认为车厢连接处空腔长度和高度对该区域气动噪声强度的影响较大，发现采用全封闭风挡可有效控制车厢连接部位气动噪声的形成。刘加利等［16］基于数值模拟，发现高速列车受电弓气动噪声为能量集中分布于100～700 Hz 的窄频带噪声。Tan等［17］采用大涡模拟和声类比方法，计算分析高速列车受电弓区域尾涡结构和气动噪声频谱特性及其声指向性，为受电弓各部件低噪声设计和优化提供理论指导。Zhao 等［18］基于声类比方法和声扰动方程计算分析高速列车受电弓结构周围流场及其气动噪声特性，发现受电弓区域气动噪声源主要为偶极子声源，对于远场辐射噪声贡献量较大的部件为受电弓弓头、弓角和上臂杆；四极子声源主要分布在受电弓结构与受电弓坑周围尾迹内，强度相对较弱。张亚东等［19］根据数值模拟，计算分析高速列车转向架区域各主要部件的气动力、速度场和气动噪声声源特性，发现转向架区域轮对、构架和制动盘等部件产生了较强气动噪声。朱剑月等［20］根据高速列车转向架简化模型，基于声类比方法和涡声理论，比较分析转向架舱结构对转向架部位流动及其诱发气动噪声的影响，发现转向架舱改变了单独转向架结构周围流场与气动噪声辐射特性，几何体表面压力脉动产生的偶极子噪声为转向架区域气动噪声主要声源。

由于高速列车结构复杂，以往研究多数根据噪声测试和数值仿真分析高速列车各关键区域时域与频域内气动噪声特性与声指向性，对于转向架区域气动噪声控制仍局限于转向架舱外侧安装裙板和转向架舱内敷设吸声板等传统措施［21-23］，降噪效果有限。

本文针对高速列车车头一位转向架直接受到来流冲击诱发产生较强气动噪声的特点，通过排障器底部设置凹坑研究高速列车转向架区域气动噪声降噪途径。基于数值计算，由高速列车排障器与转向架区域简化模型获得降噪效果后，进行高速列车车头比例模型的数值模拟与声学风洞测试，比较分析排障器底部后端区域设置凹坑对车头排障器、转向架区域流场动力性能及气动噪声特性的影响，揭示基于排障器底部后端扰流的转向架区域气动噪声降噪机理，实现高速列车车头关键区域气动噪声有效控制。

1 基于声类比方法的气动噪声预测

高速列车周围流动位于低马赫数区域，由列车各几何体表面压力脉动形成的偶极子声源是气动噪声主要声源，可将列车周围流场视为不可压缩流体进行数值模拟［24］。因此，三维非定常不可压缩Navier-Stokes（N-S）方程被用来进行高速列车流场的模拟计算，其连续性方程和动量方程分别为

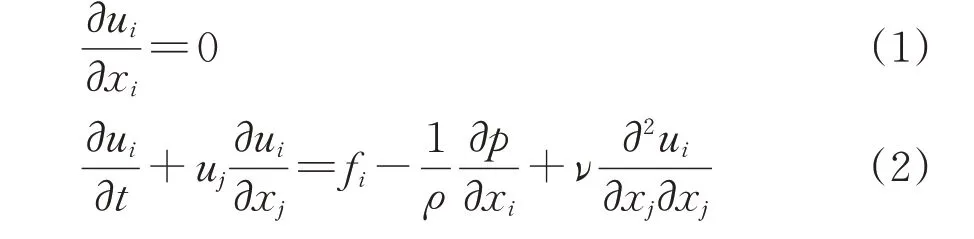
式中：xi或xj为笛卡尔坐标系的3个方向（i=1，2，3；j=1，2，3）；ui为流体速度；t为时间；fi为体积力；p为压力；ρ为密度；ν为运动黏性系数。

基于开源软件OpenFOAM®进行流场数值模拟，对流项和扩散项采用二阶离散格式，时间差分采用二阶隐式格式。

通过不同数值分析软件所得计算结果的比较分析，验证了分离涡模型进行气动声学问题计算模拟的准确性［25］。因此，基于延迟分离涡模型（Delayed Detached-Eddy Simulation，DDES）进行流场数值计算：列车各几何体表面附近的边界层区域采用基于雷诺平均（Reynolds-Averaged Navier-Stokes Simulation，RANS）模型进行求解，边界层外主体流动分离区域则应用大涡模拟（Large-Eddy Simulation，LES）模型进行求解。

根据Lighthill 声类比方法，以达到统计意义上稳定后的近场瞬态流场数据作为源项对远场辐射噪声进行预测。Ffowcs Williams 和Hawkings 假设流场参数为广义函数，建立适用于可穿透面的广义波传播方程—Ffowcs Williams-Hawkings（FW-H）方程［26］，其解为

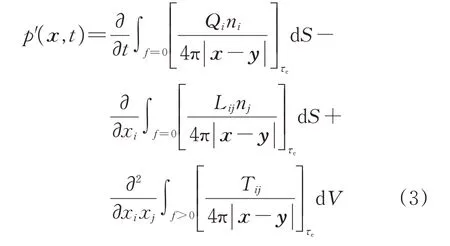
式中：x为观测者位置矢量；y为声源位置矢量；p'(x，t)为声压，即观测者在位置x处、时间t时接收到的压力；[ ·]τe为声源时间τe；S为声源积分面，被描述为函数f(x，t)=0；V为声源体积；ni或nj为对应于积分面单位法向量n的各分量；Qi和Lij分别为厚度噪声（Thickness noise）与载荷噪声（Loading noise）；Tij为Lighthill应力张量［27］。

采用基于时间延迟的积分方法进行FW-H 方程的数值求解［28-29］。

2 基于排障器与转向架区域简化模型的仿真计算

为了由数值模拟计算得到影响远场气动噪声预测精度的微小流体脉动，采用结构化网格划分计算区域，以提高流场数值计算结果的准确性。

采用基于Spalart-Allmaras 湍流模型的DDES模型对几何体壁面边界层流动进行数值求解。为缓解对超算资源较高的要求，建模时简化转向架结构，保留轮对与构架等主要部件，且由于排障器与转向架结构沿列车展向对称，流场作用的随机性在纵向对称面上影响较小，故为了减少仿真模拟对计算资源的过高需求，采用列车展向半车模型进行数值计算。

高速列车排障器底部与转向架区域采用如图1所示的简化1∶10缩比模型［30-31］。图中：模型1为安装普通排障器的转向架区域简化模型；模型2 为安装扰流排障器的转向架区域简化模型，扰流排障器是指在排障器底部后端设置4 排平行凹坑（长、宽、深分别为236.8，15.0 和5.0 mm），凹坑间距20 mm，转向架舱前缘距离相邻凹坑展向中心线22.8 mm。

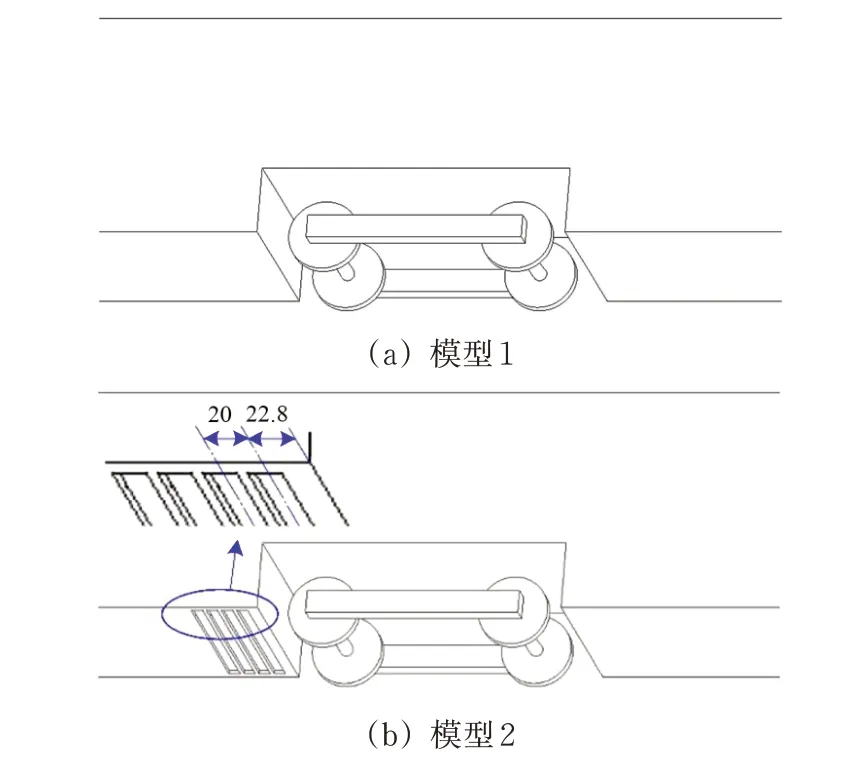
图1 排障器底部与前转向架区域简化模型（单位：mm）

网格划分时边界层内近壁面第1 层网格至列车几何体表面距离为10 μm，并以1.1 的增长率沿着固体表面法向方向向外拓展，使得近壁面第1层网格至列车几何体表面的无量纲距离y+小于1。工况1（采用模型1）和工况2（采用模型2）的计算区域内各生成3 000 万和3 100 万个六面体网格，图2所示为转向架区域的结构网格划分。

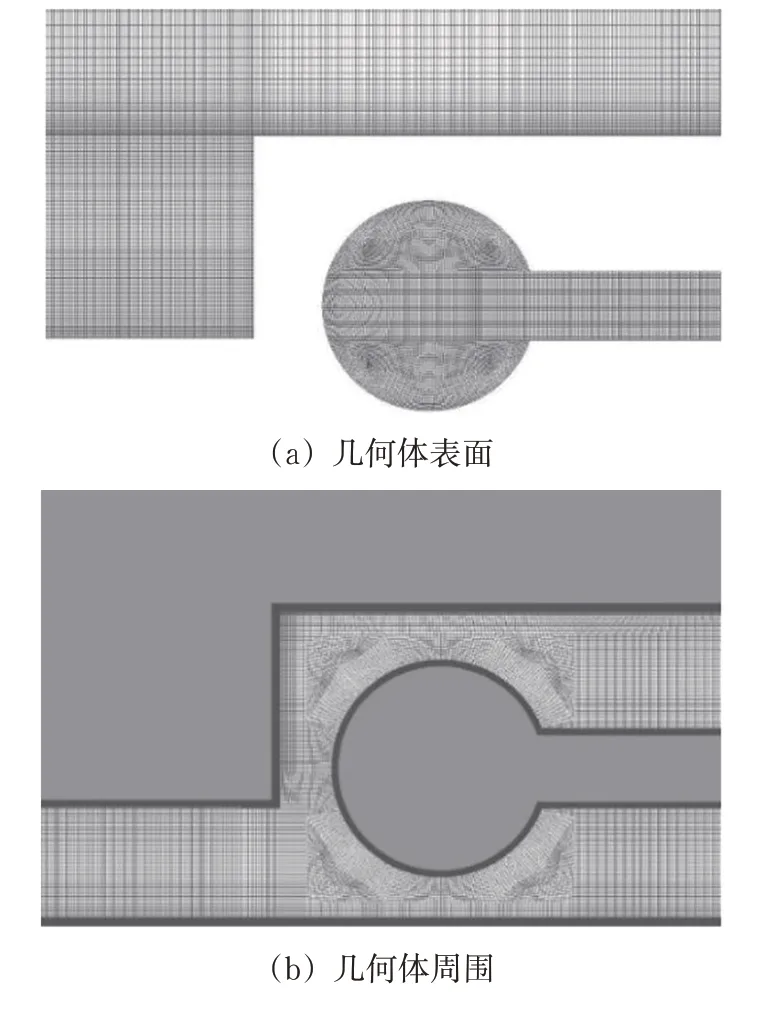
图2 简化模型结构网格划分

计算域内各边界条件设置如下：来流设置为湍流强度低于0.5%的低湍流度均匀流（U∞=30 m·s-1）；顶面与2 个侧面均设为对称面，相当于无剪切滑移壁面，忽略边界层求解；除车轮外的几何体固体表面设为静态无滑移壁面；出口定义为压力出口；为了在数值风洞模型中模拟运动列车运行于静止地面的实际情况，采用运动无滑移壁面定义车轮表面，模拟旋转效应的转动角速度根据入口来流速度确定；采用运动无滑移壁面定义地面，移动速度与入口来流速度相同。数值迭代时间步长取为5 μs，使得主要计算区域内柯朗-弗里德里希斯-列维（Courant-Friedrichs-Lewy）数（uΔ，其中u为流体速度，Δt为时间步长，L为网格尺度）小于1。

采用相同网格划分技术的转向架算例的气动噪声数值计算得到了声学风洞试验验证［20，31-32］，表明了所用数值模拟方法的准确性。

2.1 流场特性

湍涡相互作用较强部位会诱发固壁表面压力脉动的形成，从而产生气动噪声，向车内和远场辐射［24，26］。为阐明排障器周围流场特性、揭示其对转向架区域气动噪声产生的影响，对上述2 个工况下数值模拟结果中转向架区域流场的Q准则等值面、湍动能及列车几何体表面压力脉动等物理量进行比较分析。

基于Q准则得到α（α=Q/[(U∞D)2]，其中Q为速度梯度张量第二不变量，D为车轮直径）为25 时的等值面，采用无量纲化速度系数|U|/U∞（其中，u1，u2和u3为流体沿x，y和z方向的速度）进行着色，得到2 个工况下流场内转向架周围湍涡结构如图3 所示。由图3 可见：流体在转向架舱前缘发生流动分离后，与舱内转向架各几何体产生流体相互作用，在转向架构架外侧形成大尺度相干涡，在转向架舱内产生大量不规则湍涡，不同尺度涡结构之间相互作用并沿流向下游传播，对转向架舱后壁面和后缘产生了较强的流动冲击，使得转向架舱顶部车体边缘以及后缘处涡发展集中，湍流度较高；与工况1 相比，工况2的湍涡结构发展较为均匀、速度幅值有所降低，转向架构架外侧以及转向架舱后缘部位的大尺度相干涡结构明显减少且强度较低。

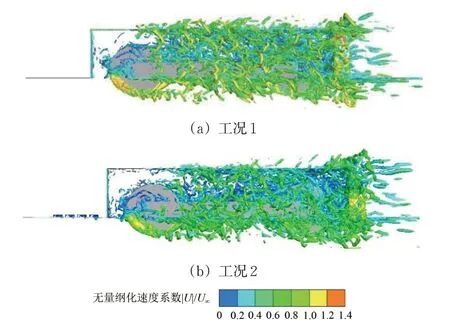
图3 不同工况下转向架周围涡结构（侧视图）

在转向架舱前缘与前轮的间隙内设置监测点，其流向速度系数Ux/U∞的功率谱密度幅值如图4所示；转向架阻力系数Cd的功率谱密度幅值如图5所示。由图4 和图5 可见：140 Hz 频率以下，工况2流向速度系数的幅值总体上低于工况1；50 Hz频率以下的低频区域内，工况2 转向架阻力系数的幅值明显低于工况1。

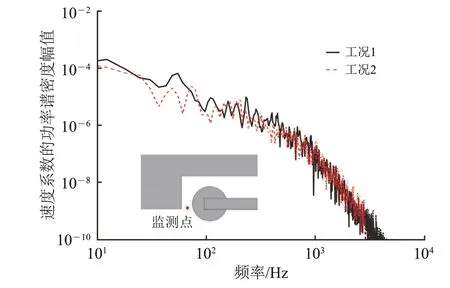
图4 流向速度系数功率谱密度

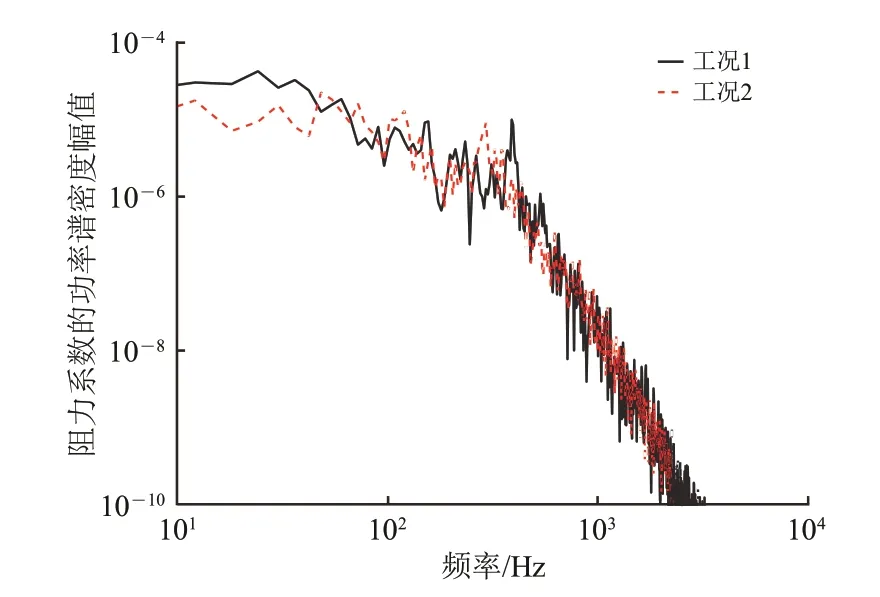
图5 转向架阻力系数功率谱密度

列车模型沿轮对中心水平切割面上的湍动能k为流体3 个方向脉动速度分量：为平均速度）分布如图6 所示。由图6 可见：与工况1 相比，工况2 下转向架周围和转向架舱后壁的流体脉动量较少，湍流强度相对较弱，由此将诱发较小的几何体表面压力脉动。

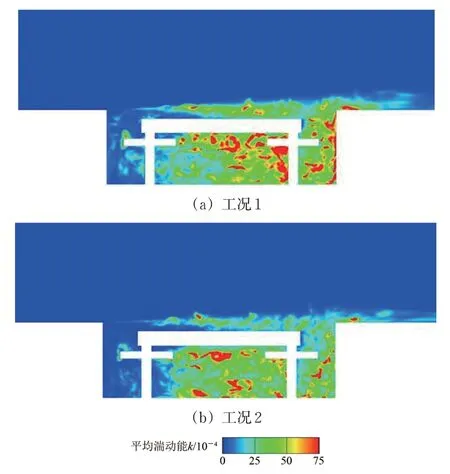
图6 简化模型湍动能（仰视图）

针对上述结果分析其原因，这是由于工况2 下排障器底部后端平行设置的凹坑结构改变了排障器周围流动状态，缓和了排障器后缘与转向架舱前缘的流体剪切作用，抑制了排障器底部后端壁面附近的剪切层发展和流动分离，减弱了排障器后缘产生的尾迹、转向架结构的流动冲击和流体相互作用。

为了进行列车各几何体表面气动噪声源比较，得到转向架区域几何体表面压力脉动分布Lp其中pref为参考声压，即20 μPa）如图7 所示。由图7 可见：与工况1 相比，工况2下列车几何体表面压力脉动较强的区域显著缩小，尤其是在转向架舱前半部分和转向架前轮对等部位，表明排障器底部后端采用凹坑进行扰流，减弱了排障器后端及转向架舱前缘剪切层涡流形成、转向架舱内涡流发展和转向架后端尾迹涡脱落产生等强度，降低了不同涡流结构与转向架舱以及转向架结构等因边界干涉诱发的壁面压力脉动，从而将有效削弱由列车几何体表面压力脉动诱发的偶极子声源产生的辐射气动噪声强度。

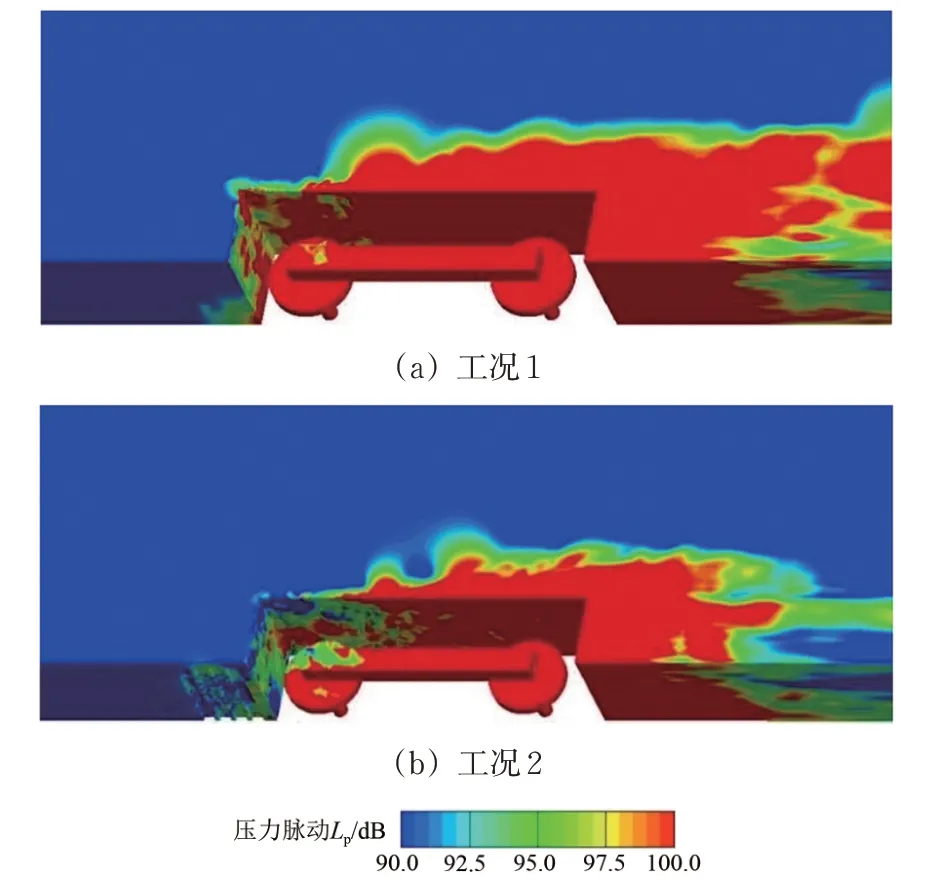
图7 简化模型几何体表面压力脉动

2.2 远场气动噪声特性

对于工况1 和工况2 下的算例，流场数值计算稳定后继续运行0.3 s，以采集列车各几何体表面压力脉动值，进行远场气动噪声预测，基于Welch方法编制的信号处理程序对远场噪声时间序列进行频谱分析［30-32］，然后再进行声压级的计算。远场声接收点位于车体侧向位置，正对转向架中心点且距离为2.5 m 处。2 个工况下简化模型远场辐射噪声频谱如图8 所示。由图8 可见：在1 kHz 以下的多数频段内，工况2 下所产生气动噪声的功率谱密度幅值较低，相应的总声压级为65.5 dB，比工况1 算例的总声压级66.6 dB 降低了1.1 dB；如前所述，这是由于工况2 下在转向架舱前缘的排障器底部后端设置凹坑后，干扰了转向架区域大尺度湍涡的形成与脱落，减弱了该部位湍涡强度、输运速度及其展向相干性，从而降低该区域气动噪声的产生。

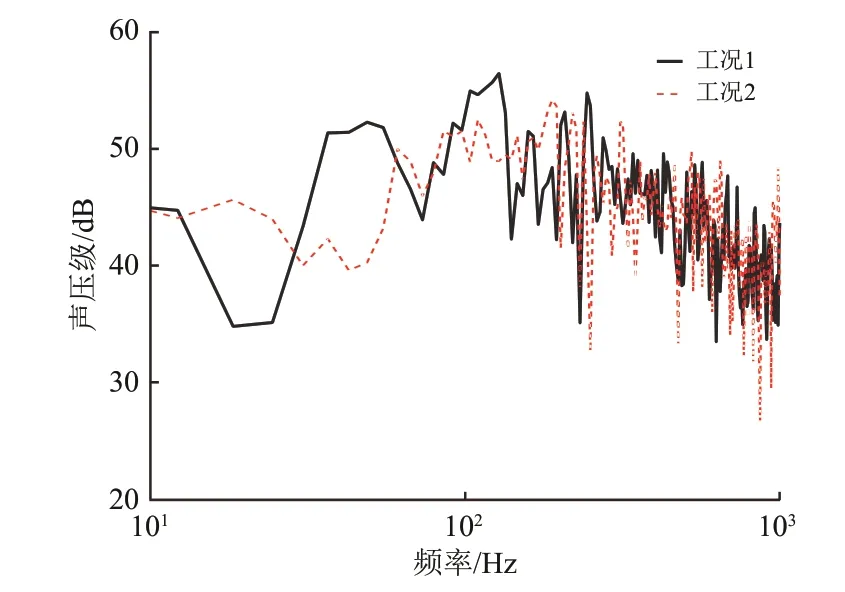
图8 远场辐射噪声频谱（计算值）

3 基于高速列车车头比例模型的仿真计算

通过采用高速列车转向架区域简化模型进行数值模拟，确定进行排障器底部扰流控制可以获得气动噪声降噪效果后，将该措施应用于高速列车车头比例模型，进一步分析其在实车比例模型上的降噪效果。

高速列车车头数值计算模型如图9 所示。图中：车头比例模型（1∶3）包含车体、鼻锥、排障器、转向架舱、转向架和尾端等结构，长、宽、高分别为5.8，1.4和1.1 m，为避免车体后端流体流动分离诱发气动噪声产生，车体尾部设计为流线型导流段。高速列车模型车头底部分别采用普通排障器（工况1）和设置凹坑的排障器（工况2）。

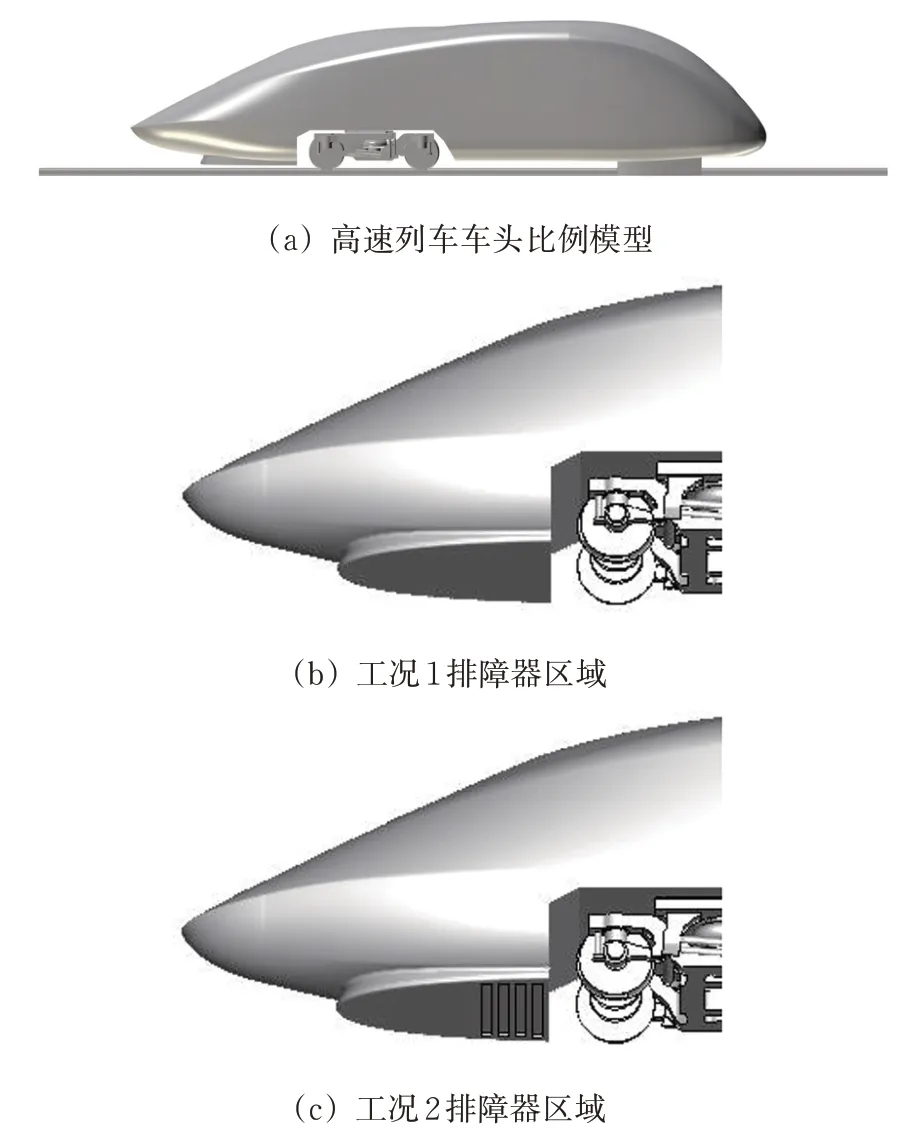
图9 高速列车车头数值计算模型

由于高速列车车头几何模型结构复杂，为缓解对计算资源的较高要求并提高数值计算效率，采用大涡模拟方法结合壁面适应局部涡黏模型（Walladapting Local-eddy Viscosity）进行流场仿真计算。基于高速列车3 车编组缩比模型网格拓扑技术［11］，在完成网格无关性分析基础上，采用适应性较强的非结构化Trim 网格进行网格划分，总网格数为1.2 亿个，计算模型横向中截面车体周围网格如图10所示。

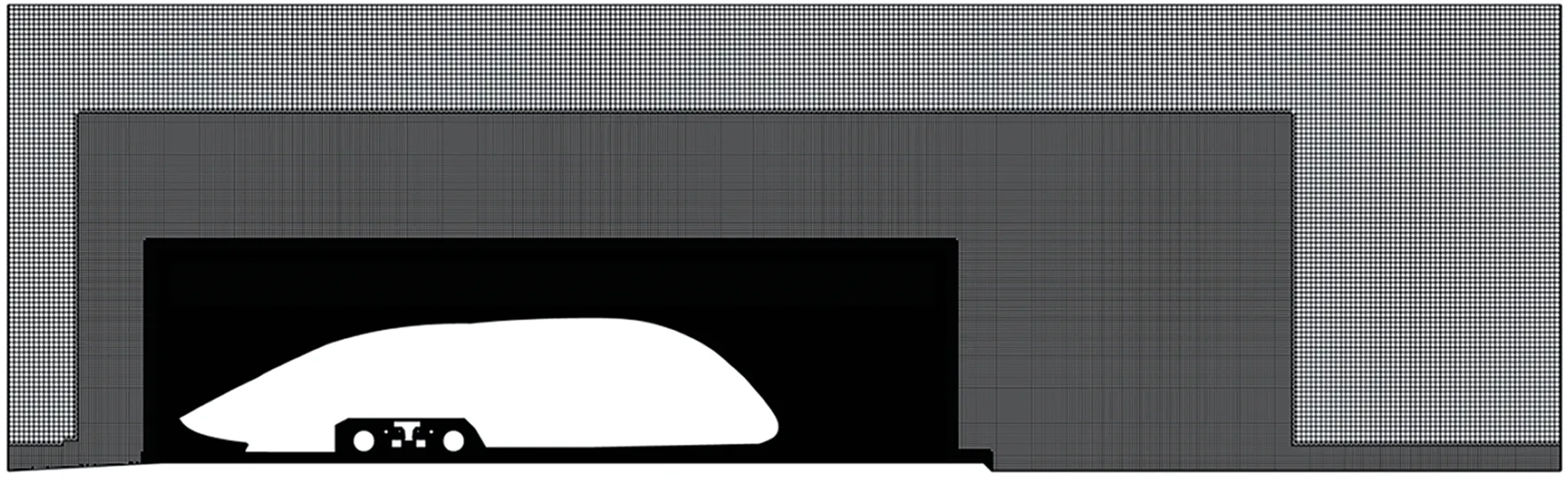
图10 高速列车车头模型横向中截面车体周围网格

3.1 流场

数值模拟250 km·h-1来流速度下、低湍流度（≤0.5%）时2 个工况下转向架区域采用Q准则显示的湍涡结构等值面（α=100）如图11 所示。由图11可见：与工况1相比，工况2 下排障器底端形成的剪切层出现了较明显的大尺度拟序结构，干扰了前轮对区域几何体表面流体产生的流动分离，使得前轮对底部区域大尺度涡相对较少，涡强度有所降低，从而减弱了转向架周围流动发展。

图11 列车车头模型转向架周围涡结构（侧视图）

2 个工况下转向架区域横向中截面湍动能分布如图12 所示。由图12 可见：工况2 下转向架舱底部与后缘区域湍动能强度明显减弱；如前所述，这是由于工况2 中在排障器底部后端设置了多排平行凹坑结构，起到较好的流动阻滞作用，气流流经转向架舱前缘时流体流动分离形成的剪切层与涡脱落强度得到减弱，从而缓和了转向架结构受到的流动冲击作用。

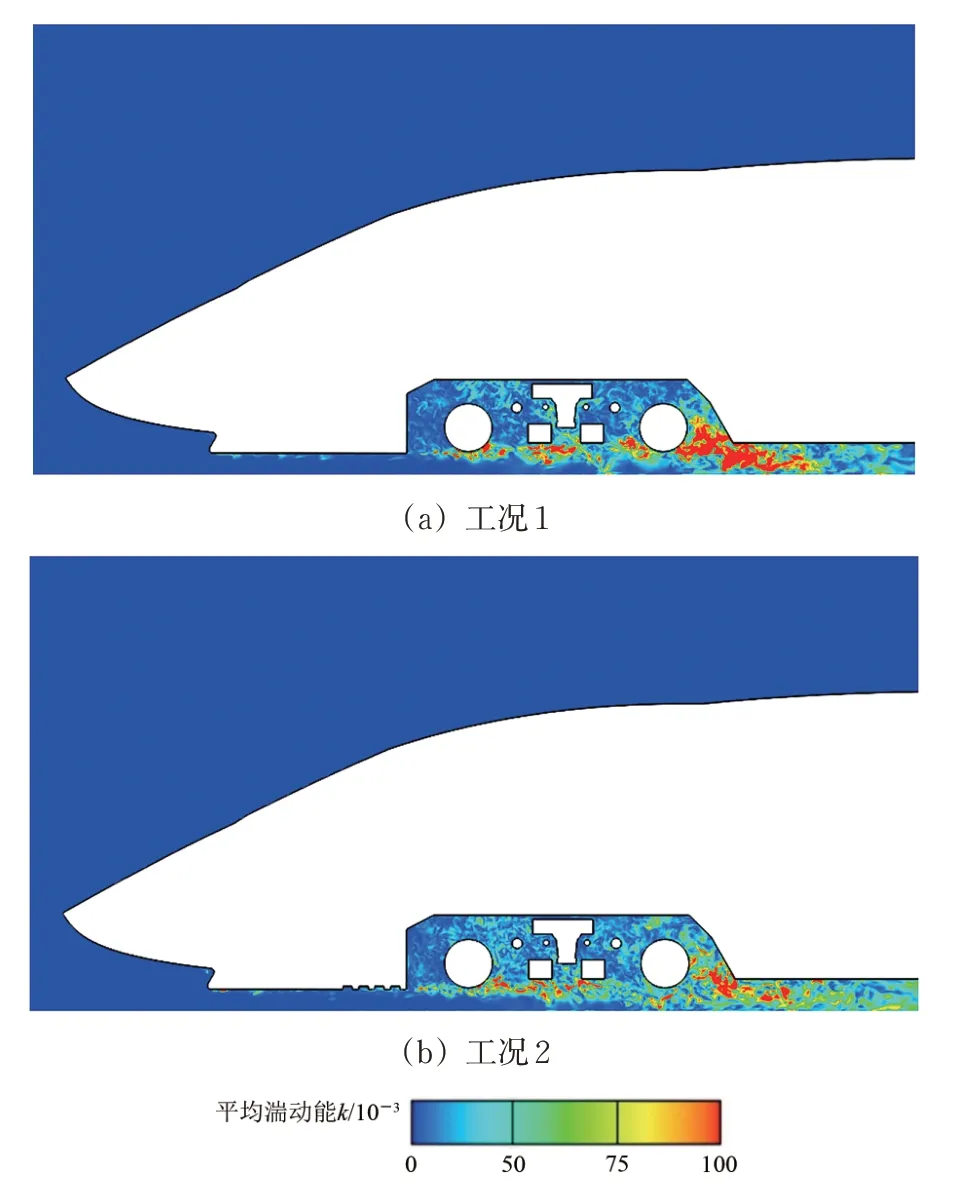
图12 车头模型转向架区域横向中截面湍动能分布（侧视图）

3.2 远场噪声

高速列车车头模型气动噪声计算时，在远场设置10 个声接收点，位于侧向距离转向架中心6 m、离地面高度分别为0.6，1.1 和1.6 m处，各声接收点间相对位置如图13所示。

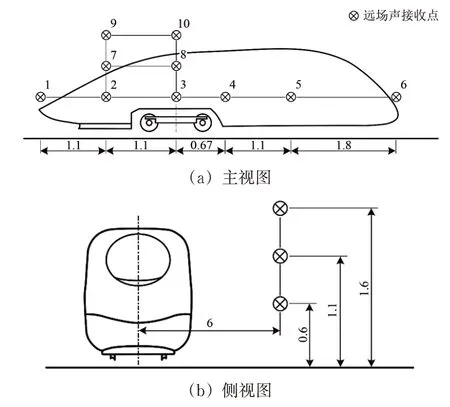
图13 远场声接收点分布（尺寸单位：m）

5 kHz 频率以下2 个工况的远场气动噪声总声压级见表1。表中：降噪量为工况1 下各声接收点的总声压级减去工况2 下相对应的数值。由表1 可知：工况2 较工况1 各声接收点的总声压级均有一定的降幅，其中转向架舱后端（测点6）、车体中部区域（测点5）总声压级降幅明显，降低约0.3～0.7 dB（A），取得了较好的降噪效果。

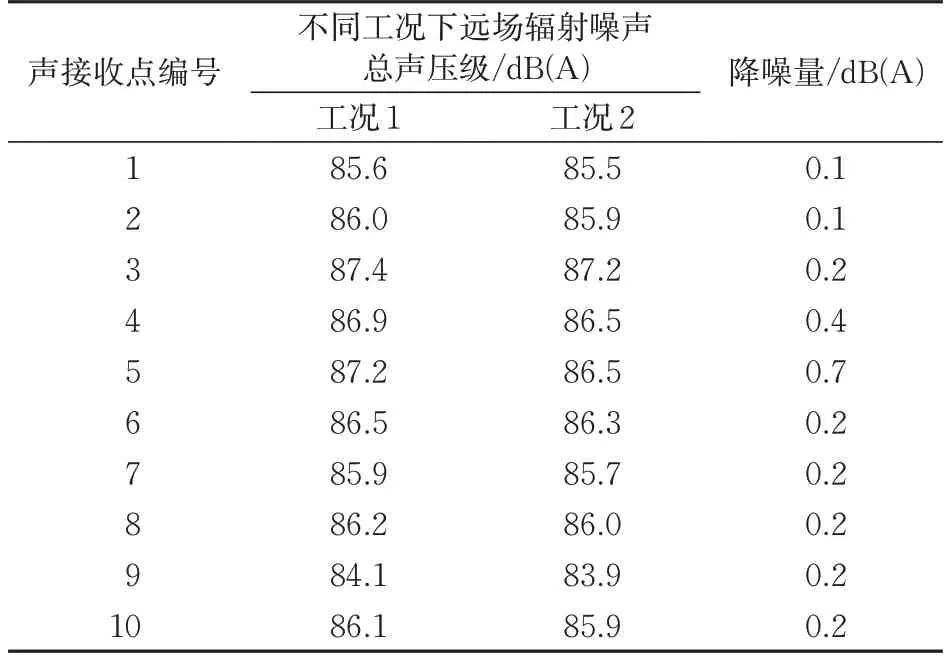
表1 不同工况下远场辐射噪声总声压级计算值

4 基于高速列车车头比例模型的风洞试验

在同济大学地面交通工具声学风洞内，进行排障器底部后端设置凹坑的高速列车车头模型气动噪声降噪效果测试。该风洞为3/4 开口回流式风洞，半消声室设计，喷口面积为27 m2，试验段有效长度为15 m，在160 km·h-1风速下风洞背景噪声低于61 dB（A），静压梯度小于0.001 m-1。试验时来流速度为250 km·h-1，湍流强度低于0.5%。与数值计算模型相似，试验模型为高速列车车头1∶3 比例模型，如图14 所示。图中：U0为均匀来流速度；传声器阵列位于车体侧向位置、正对转向架中心且距离列车模型纵向中心线5.8 m处。

图14 声学风洞内列车模型

试验模型被固定在风洞试验段的支撑地板上，支撑柱均采用翼型设计，以减少其对流动形成的干扰，通过激光定位仪确保试验模型位于风洞喷口纵向中心线上。在列车模型的车头底部分别安装底部平滑的普通排障器与底端设置凹坑的排障器，进行风洞试验。

试验时采用表面传声器测量车体底面（转向架舱顶面）压力，采用自由场传声器测量远场辐射噪声声压，数据采集时采样频率设为48 kHz、采样时间设为10 s，通过快速傅里叶变换将所得时域信号进行频域转换后获得远场测点声压级频谱和总声压级。

高速列车车头模型气动噪声测试时远场布置10 个传声器，各测点间相对位置与仿真计算相同。声源识别测试时，在试验段流场外布置120 通道传声器阵列，采用多通道测量分析设备获取声源噪声分布云图。声阵列上各传声器采集声压信号后，通过延时求和对各空间角的声源信号进行重构，实现声源定位［33］。基于传统互谱算法的声源识别计算式为

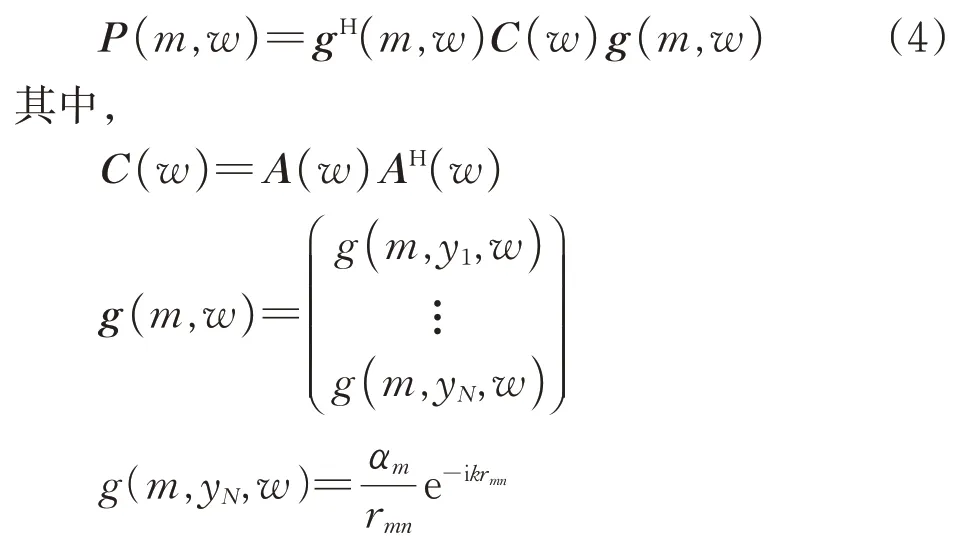
式中：P(m，w)为声源平面位于m点处在w频段内的声功率；g(m，w)为导向矢量，指向声源平面网格点m，表示位于声源平面网格点m处的单位强度点声源到达声阵列上各个传声器的时延与幅值衰减；yN为声阵列上第N个传声器所在位置坐标值；N为声阵列上传声器总数；gH(m，w)为g(m，w)的共轭矩阵；C(w)为传声器阵列所得信号的互谱矩阵；A(w)为声阵列w频段内声压幅值矩阵；AH(w)为A(w)的共轭矩阵；i 为虚数单位；k为波数；rmn为声源平面网格点m与声阵列上第n个传声器间的距离；αm为归一化因子。

安装普通排障器（工况1）与底端设置凹坑的排障器（工况2）的高速列车模型车体底面压力脉动1/3倍频程曲线如图15所示。图中：车体底面压力脉动测点位于转向架舱前端顶部车体中心线上、距离转向架舱前壁面50 mm 处。由图15 可见：工况2下车体底面压力脉动在200 Hz以上频率时均小于工况1，尤其在200～1 250 Hz频率范围内的声压级降幅较大，在20 kHz 以下频率内车体底面压力脉动总声压级降低0.9 dB（A），说明排障器底部后端设置凹坑进行扰流后，有效抑制了转向架舱部位流体分离和涡脱落，减弱了流动与转向架以及转向架舱壁面间的流体相互作用，从而降低了车体底面产生的压力脉动，与数值计算阐明的转向架区域涡流与壁面压力脉动之间的关联机理相吻合。

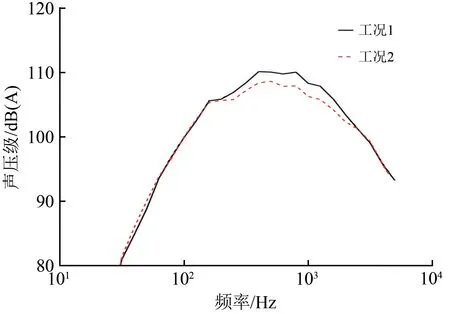
图15 车体底面压力脉动1/3倍频程曲线（测试值）

2 个工况下各测点在5 kHz 以下频率内远场总声压级试验值见表2。由表2 可知：车头鼻锥（测点1）、车尾（测点6）与车顶（测点9 和测点10）位置降噪较少，降噪量为0.1～0.2 dB（A），排障器部位（测点2 和测点7）降噪量为0.2～0.3 dB（A），转向架区域（测点3 和测点8）降噪量为0.3～0.4 dB（A），而转向架舱后缘及其下游部位（测点4 和测点5）降噪量可达0.4～0.5 dB（A），与数值计算得到的远场各声接收点均有一定的降噪效果、而转向架舱后端区域降噪效果最明显的结果相一致。由此可见，列车排障器底部后端采用凹坑进行扰流控制后，有效降低了转向架周围与转向架舱后缘区域产生的气动噪声。

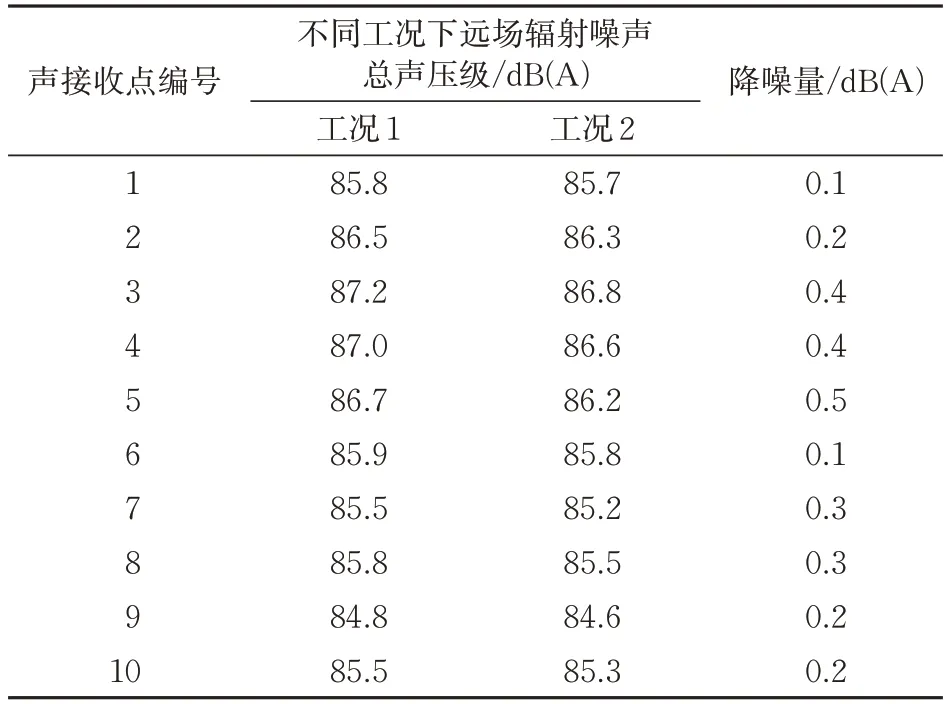
表2 不同工况下远场辐射噪声总声压级试验值

测点4 在2 个工况下的远场气动噪声1/3 倍频程曲线如图16所示，工况1下的数值计算与风洞试验结果对比如图17所示。

由图16 可见：在100～1 300 Hz 频率范围内，工况2 较工况1 声压级幅值的降幅较明显，最大降幅达1.8 dB（A）。由图17 可见：数值计算与风洞试验结果的声压级曲线吻合良好（尤其在幅值较高的频域内），3 kHz 以下频率的总声压级计算值与试验值误差为0.1 dB（A），因此声学风洞测试结果验证了气动噪声数值计算结果的准确性。

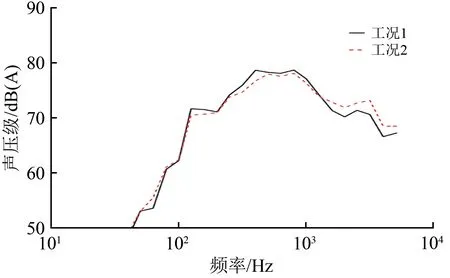
图16 远场辐射噪声1/3倍频程曲线（试验值）

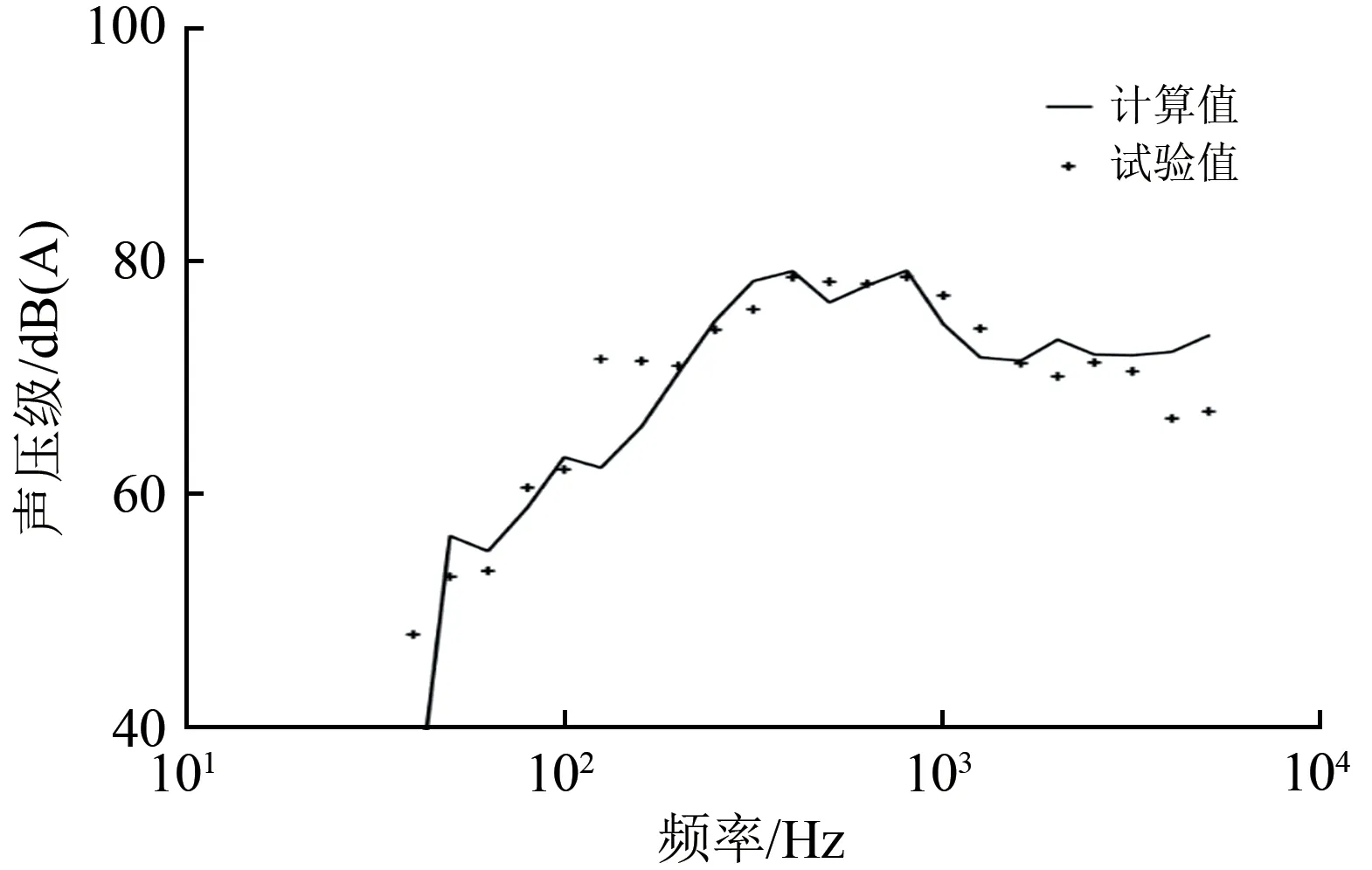
图17 气动噪声计算试验验证

2 个工况下由置于流场外的传声器阵列（如图14 所示）测得的噪声源分布云图如图18 所示。由图18 可见：列车头车模型采用底部后端设置凹坑的排障器后，20 kHz 下全频段范围内转向架周围噪声源区域面积得到显著减小，噪声幅值降低了1 dB（A）左右，气动噪声降噪效果良好。

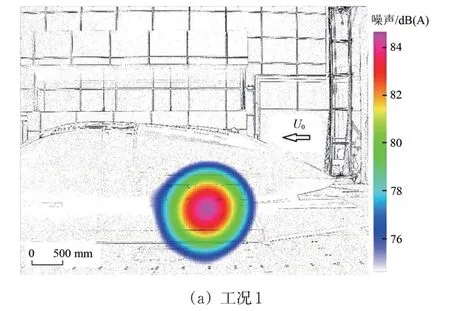
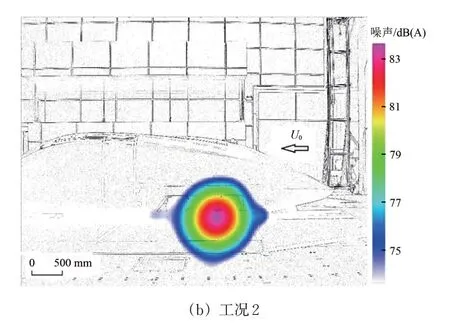
图18 列车模型气动噪声源云图（250 km·h-1）

5 结论

（1）排障器底部后端采用凹坑进行扰流，可以干扰排障器尾端与转向架舱前缘剪切层流动分离，阻滞流动发展，减弱转向架前轮对区域大尺度湍涡的形成与发展，抑制不同涡流结构与转向架区域几何体的流动冲击和流体相互作用，降低转向架舱与舱内各几何体结构因边界干涉诱发产生的表面压力脉动，从而有效降低转向架部位气动噪声的产生以及向远场辐射。

（2）高速列车车头比例模型声学风洞气动噪声测试表明：排障器底部后端设置凹坑后，转向架舱前端顶部车体中心线上壁面压力脉动总声压级、车体侧向对应转向架与转向架舱后缘部位远场测点气动噪声降幅明显，降噪效果良好；声阵列测得转向架部位噪声源面积缩小，在20 kHz 频率下声压级降幅为1 dB（A），气动噪声得到有效控制；声学风洞测试结果验证了数值计算得出的排障器底部后端布置平行凹坑进行扰流后获得的气动噪声控制效果。

（3）对于实际运行的高速列车车辆，基于参数设计和优化，可在排障器底端设置不同形状的凹坑结构（如长条形、正方形、菱形与圆形等）进行扰流，从而有效降低转向架区域（尤其是前轮对部位）复杂流动诱发气动噪声的产生。