基于响应面法和粒子群算法的桥梁高耸临时提升支架优化

占玉林，许江辉，许 俊，邵俊虎，林智敏，何 鹏

（1.西南交通大学 土木工程学院，四川 成都 610031；2.中铁第四勘察设计院集团有限公司，湖北 武汉 430063；3.成都大学 建筑与土木工程学院，四川 成都 610106；4.中铁上海工程局集团第五工程有限公司，广西 南宁 530200）

钢拱桥具有造型美观、跨越能力大、施工方式灵活等突出优点，使其在桥梁建设领域中得到广泛应用。常见的钢拱桥形式有钢管混凝土拱桥、钢箱拱桥等［1-3］。其施工方法大致分为：支架施工法、悬臂拼装法、转体施工法以及缆索吊装法等［4-6］。支架整体提升方法属于支架施工法的1种，起初应用于建筑领域，随着整体提升技术的不断成熟，其凭借着拼装精度高、结构整体性好和施工安全可靠等优点在大跨径拱桥施工中逐渐得到推广应用［7-8］。拱肋整体提升支架作为大跨径拱桥进行安全吊装施工的重要结构，其在施工过程中受力复杂，强度和稳定性问题十分突出。若支架尺寸过小，会造成结构的强度和稳定性降低，危及施工安全；而支架尺寸过大，则其利用率较低，增加工程造价［9-10］。目前，提升支架的设计计算理论尚不完善，在确定提升支架结构参数时，需综合考虑其安全性和经济性［11］。

目前，大量学者通过响应面法［12-14］对结构优化设计进行了广泛研究。徐征杰等［15］通过构建响应面函数获得强风化花岗岩地层在不同盾构推进速度下的最优改良参数；成棣等［16］研究了多项式响应面优化方法和高斯径向基函数响应面优化方法对于车轮踏面的优化效果，发现响应面方法适用于车轮踏面优化，优化后的车轮踏面磨耗指数降低明显；宗周红等［17］基于响应面方法成功对大跨径连续刚构桥健康监测有限元模型进行了修正，模型优化后计算得到的频率跟实测频率较吻合。Ren等［18］将响应面法应用于土木工程结构的结构动力学中，通过仿真数据构建二次多项式响应面，并通过简支梁和预制连续梁验证了模型的准确性，与传统方法相比，该法高效且易收敛。

虽然上述学者通过理论分析、数值计算等方式对结构进行了优化，但实际工程中结构各优化目标参数的随优化设计参数的变化规律往往并不统一，且可能相互冲突，协调其关系，实现结构的最优化有待研究。

本文针对桥梁高耸临时提升支架（以下简称“提升支架”），建立相应的数值模型，在运用响应面法求得提升支架各优化目标参数响应面函数的基础上，构建提升支架的目标优化函数，采用粒子群优化算法寻找最优解，得到提升支架的合理结构形式。

1 基于响应面法和粒子群算法优化的基本原理

针对工程结构优化，本文提出一种基于响应面法和粒子群算法的优化方法，其基本流程如图1所示。

图1 工程结构优化流程图

1.1 响应面法基本原理

响应面法（Response Surface Method，RSM）由Box 等［19］于1951 年提出，是一种构建近似函数的方法。利用响应面法构造近似函数时，首先要确定近似函数的形式，然后运用统计试验设计方法在空间内选取足够多的样本，最后运用最小二乘法原理拟合试验设计样本的分析结果得到响应面函数。通常响应面函数采用二阶函数形式，即

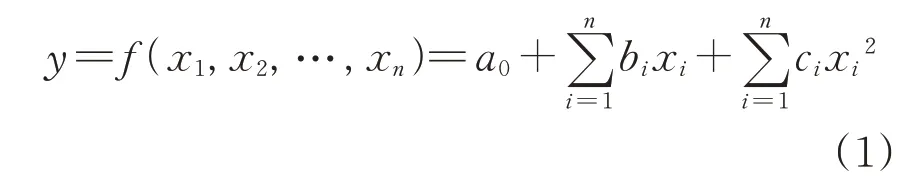
式中：xi为设计参数；a0，bi和ci为待定系数，需由试验样本进行确定；n为设计参数个数。

响应面函数的待定系数向量A可由下式计算

式中：Y为响应面函数预测向量；X为优化参数矩阵；m为求解待定系数所需试验样本数量。

1.2 目标优化函数

与单目标优化问题不同，由于多目标优化问题（Multi-objective Optimization Problem，MOP）［20-21］中的各个子优化目标间可能相互冲突，无法令所有优化目标参数均达到最优解，因此，需要寻找一组使所有优化目标函数尽可能达到最优的设计参数值。为获得最优解，本文基于多个优化目标函数，将多目标优化问题转变为单目标优化问题，考虑到各参数的量纲不同，为了便于统一求解，对各目标优化函数进行无量纲化处理，即

式中：yi为第i个目标优化函数；yimax和yimin分别为yi的极大值和极小值。

则目标优化函数Y可表示为

式中：ki为各优化目标参数的权重系数。

1.3 粒子群优化算法原理

粒子群算法（Particle Swarm Optimization，PSO）是由Eberhart和Kennedy于1995年首次提出用于解决全局优化问题的智能算法［22］。粒子群算法将粒子视为没有体积和质量的点，并为每个粒子设置速度和位置2 个参数。每个粒子以自身的最佳位置作为局部最优目标，以种群历史的最优位置为全局最优目标，在空间中进行运动［23-25］。每个粒子代表解空间的1个候选解，解的优劣度由适应度函数决定，本文中适应度函数为目标优化函数Y。粒子群算法的进化方程为

式中：i为粒子编号；j为粒子所处空间的位置；t为粒子迭代次数；vij为粒子速度；xij为粒子位置；pij为粒子i在第j维的最优位置；pgj为全部粒子在第j维空间的最优位置；w为惯性权重系数［26］；c1和c2为学习因子，取值范围为1～2.5［19］；r1j和r2j为相互独立的0～1之间的随机数。

2 桥梁高耸临时提升支架优化目标函数

某大跨径提篮式钢箱拱桥在施工过程中，中拱段采用低位拼装+高耸门式支架整体提升，如图2所示。提升支架为高87.5 m的钢结构，钢管材料采用Q235 级钢材，并由焊接拼装制成。其中，承台以上13.6 m范围内，采用钢管混凝土，其余部分采用空心钢管，支架由立柱与横撑组成，立柱钢管直径为1 520 mm。由于提升支架高度高、提升重量大，提升过程安全风险大，且造价高，为使得其兼顾受力性能与造价，对提升支架结构进行优化。

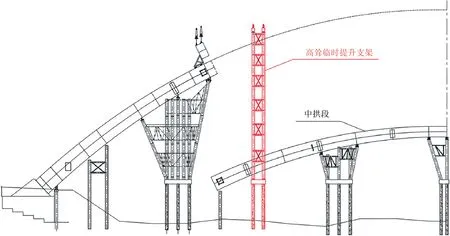
图2 桥梁高耸临时提升支架整体提升现场施工示意图

2.1 优化设计参数和优化目标参数选取

提升支架作为拱肋提升过程中的主要承重结构，对结构强度和稳定性要求较高，需保证其在拱肋提升过程中的受力和变形的安全性［27］。因此，选取钢管混凝土立柱内混凝土填充高度x1、钢管外径x2和钢管壁厚x33个对提升支架结构性能影响较大的因素为优化设计参数，其原始设计值分别为：x1初=13.6 m，x2初=1 520 mm，x3初=16 mm。充分考虑提升支架的尺寸设计要求和实际情况，优化参数x1、x2和x3的上下限取值分别为［0，27］m，［1 000，2 000］mm 和［10，22］mm。在保证提升支架结构受力性能的同时，还应考虑经济性要求，因此选取最大拉应力y1、最大压应力y2、屈曲系数y3和工程造价y4作为提升支架的优化目标参数。

2.2 响应面函数建立

上述提升支架4 个优化目标参数的优化设计参数均为3个，因此4 个优化目标参数的响应面函数的形式为

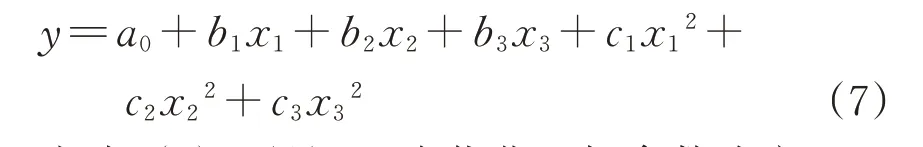
由式（7）可见，4 个优化目标参数响应面函数的待定系数均为7个，至少需进行7 次试验建立各优化目标参数的响应面函数。

为了求解优化目标参数的响应面函数，依据提升支架结构参数，运用有限元分析软件MIDASCIVIL，建立图3 所示的桥梁高耸临时提升支架数值模型。各构件均采用梁单元模拟，柱顶钢箱梁选取Q345 钢材，钢管立柱选取Q235 钢材，承台及钢管内灌注混凝土选取C30混凝土材料。桩基底部采用固结边界条件，上部钢结构与承台间采用刚性连接。施工过程中拱肋的重量以集中力的方式施加在支架顶部的钢箱梁上。

图3 桥梁高耸临时提升支架有限元模型

为保证响应面函数的精确性并验证其拟合效果，改变数值模型中的优化设计参数，共进行19组试验，数值模拟结果见表1。

根据响应面法的基本原理，对表1 中的计算结果进行多元回归拟合，得到提升支架最大拉应力y1、最大压应力y2、屈曲系数y3及工程造价y4这4个优化目标参数响应面函数的待定系数的取值，见表2。

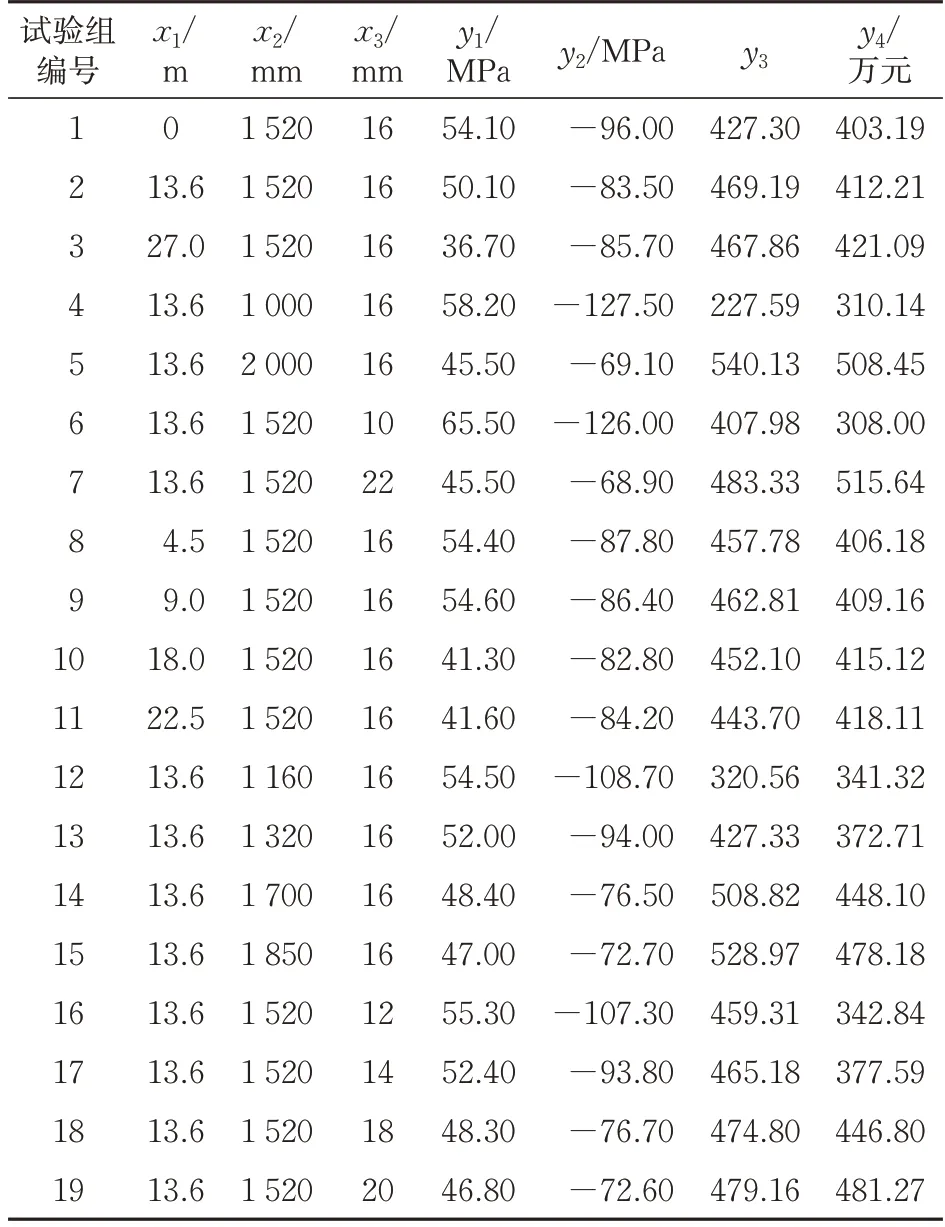
表1 提升支架数值模拟结果

表2 优化目标参数的响应面函数系数取值

为验证响应面函数的准确性以及预测能力，通过回归分析判断其拟合度。判定系数R2表示响应面函数拟合值与计算值之间的差异程度，在0～1之间取值，其值越大，则响应面函数拟合就越接近实际情况；相对均方根误差Re表示响应面函数的精度，其值越小，表示响应面函数的精度越高。响应面函数的拟合度分析结果见表3。

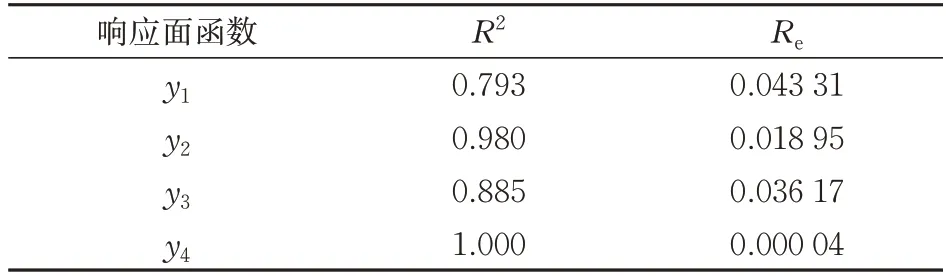
表3 响应面函数拟合度量值

由表3 可知，各响应面函数的判定系数均接近1，且相对均方根误差很小，由此验证了各响应面函数的拟合效果较好，可用于结构优化。

2.3 目标优化函数

为了构造目标优化函数Y，首先根据式（3），对4个优化目标参数的响应面函数进行无量纲化处理，得到考虑到提升支架对结构安全性和经济性的不同设计需求，引入了2 个权重系数，即安全系数α和成本系数β。则得到目标优化函数，即

当α＜β时，表示在结构满足正常使用和极限承载能力的前提下，比较注重结构的经济性；当α=β时，表示在结构设计中安全性和经济性同等重要；当α＞β时，表示在结构设计中相较结构的经济性，结构的安全性更应受到关注。

3 桥梁高耸临时提升支架优化

基于上述各优化目标参数的响应面函数及目标优化函数，根据粒子群算法的基本原理，利用MATLAB 软件编制相关优化程序进行寻优分析。粒子数目取值为40，学习因子c1和c2取值均为2，惯性权重系数w取值为0.5，最大迭代次数取为1 000，3 个自变量x1，x2和x3的取值范围分别取为［0，27］m，［1 000，2 000］mm和［10，22］mm。

由于单次寻优的结果具有一定的随机性，因此α与β取不同值，对目标优化函数进行多次优化，取优化的平均值作为最终的优化结果。α和β在不同取值情况下，各优化目标参数的计算结果见表4。

表4 不同α和β组合下各优化目标参数值

当α=0.1 或α=0.2时，结构最优优化设计参数得到造价虽然较低，但结构的最大压应力过大，安全储备小，因此过于重视结构造价而降低结构安全性是不合理的。

当α=0.3 或α=0.4时，结构的屈曲系数较大，但其不是控制结构安全性的主要参数，同时最大拉应力较小，最大压应力较大，结构的强度主要由最大压应力控制，最大压应力分别为90 和71 MPa，结构的安全储备较大，当α由0.3 变为0.4时，造价增高19.4%。

当α取0.5～0.9（对应的β取0.5～0.1）时，结构的最大拉应力、最大压应力、屈曲系数在数值上变化不大，且结构均处于较低应力水平，材料得不到充分利用，对应的造价逐渐增高，α=0.5和α=0.9时优化所得到的造价相差71.46 万元，这说明在本工程结构中，当α从0.5逐渐增加至0.9时，成本系数与安全系数的取值对优化结果的影响相对比较小。

综合上述对安全系数α和成本系数β的讨论可知，当α取为0.3左右，β取为0.7左右，结构具有一定的安全储备，同时兼顾了造价的经济性，4 个目标优化参数的优化结果能够达到相对理想的平衡。需要说明，当α取为0.3，β取为0.7时并不是绝对意义上的最优解，而是多目标优化函数Pareto前沿解集中的1个非支配解，在求该非支配解的过程中综合考虑了结构的强度、稳定性和工程造价等多个目标优化函数，它是在满足各目标优化函数取得平衡状态下的综合较优解。

优化前后提升支架的各响应面函数值如图4 所示。由图4可知：优化后提升支架的最大拉应力由50.1 MPa降低为38.6 MPa，减小幅度为23%；最大压应力由83.5 MPa 增加至90.47 MPa，增加8.3%；屈曲系数优化前后变化较小；工程造价由412.21 万元减少至405.76 万元，降低幅度为1.6%。分析结果表明，在支架最大压应力和屈曲系数变化不大的情况下，结构最大拉应力明显降低，安全度得到较大提升，此外，工程造价还能略微降低，优化效果比较可靠。

图4 优化效果对比

4 结论

（1）本文提出的响应面法和粒子群算法相结合的多目标优化方法能有效进行提升支架的设计优化。

（2）提升支架结构优化目标参数的响应面函数拟合精度较高，响应面函数可合理构建结构优化参数与优化目标参数之间的数学关系。

（3）通过引入权重系数可将工程中的多目标优化问题转变为单目标优化问题，为解决多个优化目标之间存在矛盾的情况提供了解决方法。

（4）当安全系数和成本系数分别取0.3 和0.7时，提升支架的多目标优化函数得到较优解，优化后在支架最大压应力和屈曲系数变化不大的情况下，结构最大拉应力明显降低（降幅达23%），安全度得到较大提升，此外，工程造价还能略微降低，优化效果显著。