时速600 km高速磁浮列车明线非定常气动性能数值模拟研究

杨永刚，梅元贵

（1.兰州交通大学 机电工程学院，甘肃 兰州 730070；2.兰州交通大学 甘肃省轨道交通力学应用工程实验室，甘肃 兰州 730070）

2021 年7月，世界首台设计时速600 km 等级的高速磁浮列车在我国中车青岛四方机车车辆股份有限公司成功下线，填补了高速铁路与航空运输之间的速度空白，进一步完善了现代化综合交通运输体系［1］。磁浮列车车体轻，且列车与轨道不接触，高速运行时车底升力产生脉动现象，造成车体高频振动，影响乘坐舒适性［2］。极端条件下，磁浮列车的气动升力接近列车自重，过大的气动升力易导致列车悬浮系统失效，引起车体与轨道的磨损，严重时致使车底设备与轨道发生碰撞，危及行车安全［3］。磁浮列车无轮轨摩擦阻力，气动阻力占比更大，列车以600 km·h-1速度在明线高速运行时气动阻力约占总阻力的90%。因此，气动阻力和升力问题是磁浮列车的关键空气动力学问题，必须进行深入研究。

高速磁浮列车明线空气动力学问题的研究现状如下：日本铁路公司磁悬浮分部于2002 年在日本山梨线上进行MLX01型列车及其改进列车的空气动力学试验，发现改进车型有效降低了气动阻力，提高了乘坐舒适性［4-5］；并测试车速对列车悬浮和导向间隙的影响特性，发现列车速度低于100 km·h-1时悬浮力和导向力不足，列车稳定性变差［6］。Pulliam 等［7］采用模型试验对磁浮列车气动性能进行研究，发现轨道的移动或静止对列车气动阻力影响较小，对升力影响较大，对车底表面压力影响显著。Miyakawa 和Takao 等［8-9］为MLX01 型列车设计出具有良好空气动力学性能的“双尖突”和“空气楔形”头尾车组合外形，为磁浮列车头型设计提供参考。我国在上海磁浮线用TR08 型列车进行系统的空气动力学试验，为后续研究磁浮列车空气动力学提供了试验数据［10-11］。丁叁叁等［3］对时速600 km 高速磁浮列车的气动升力进行定常数值模拟研究，发现悬浮间隙内的流场特性决定了列车气动升力的分布规律，并提出在车头和车尾底部安装导流装置的气动升力有效控制方法。Zhou等［12］对明线时速600 km 高速磁浮列车流场特征进行三维数值模拟，发现列车表面旋涡脱落使车体侧面附面层厚度明显增加，悬浮间隙和导向间隙内存在高强度旋涡。张杰等［13］采用大涡模拟方法对时速600 km 高速磁浮列车气动噪声声源特征进行数值模拟研究，发现车尾附面层分离引起的空间扰动是磁浮列车的主要气动噪声源，主要为四极子声源，车速越高，四极子辐射声能量占比越高。杨永刚等［14］对我国时速600 km 高速磁浮列车明线交会时的横向气动性能进行三维数值模拟，发现“T”轨道限制了车底气流的横向流动，增加了明线交会时车体的侧滚力矩，明线交会时，头车气动性能最为恶劣，交会压力波和侧向力峰值与车速的平方成正比。梁习锋等［15］对侧风环境下磁浮列车明线交会时的气动性能进行数值模拟，得出交会压力波和横向气动力最大值对应的风向角；横风作用下横向力近似与风速的0.8 次方成正比，侧滚力矩约与风速的1.3～1.5 次方成正比。Huang 等［16］对TR08 型列车明线运行时车体表面瞬态压力和列车风进行三维数值模拟，发现明线交会时交会压力波峰值约为单车通过时的2 倍；并根据CEN 标准［17］的列车风风速规定，给出以时速430 km 明线交会时距列车中心线3.7 m 的安全距离。舒信伟、刘堂红、周丹等［18-20］对TR08 型磁浮列车采用“比选法”进行了气动外形优化，研究水平和纵向轮廓线形状对列车气动力的影响特性，发现减小纵向轮廓线曲率和水平轮廓线宽度可有效改善列车气动性能。姚栓宝等［21］基于优化算法，采用VMF 参数化方法和曲面离散方法，进行了高速磁浮列车头型的气动优化研究，优化后整车气动阻力系数减小19.2%，头车和尾车气动升力系数分别减小24.8%和51.3%。

纵观上述研究，发现对高速磁浮列车明线气动性能的研究主要是针对我国TR08 型和日本磁浮列车；对时速600 km 高速磁浮列车明线气动性能研究的公开成果较少，且目前的研究主要是将明线稳定运行简化为定常流动问题。磁浮列车明线稳定运行时列车气动力具有明显的非定常特性，且升力非定常振荡对列车垂向平稳性和舒适性有显著影响［2，12］。因此，有必要对时速600 km 高速磁浮列车明线稳定运行时的非定常气动性能进行研究。

由于目前没有时速600 km 磁浮列车的达速试验线，线路试验无法实施，而且线路试验测量中气动升力无法测量［22］。列车风洞试验与实际运行时的气动力有明显差异［23-25］，且目前国内大型磁浮风洞领域尚属空白［26］。因此，数值模拟是目前开展时速600 km 高速磁浮列车明线气动性能研究的主要手段。

本文采用改进延迟分离涡（IDDES）方法，对时速600 km 高速磁浮列车明线稳定运行进行数值模拟，分析列车周围非定常流场特性、气动力的时域和频域特性，明确各部件的气动力贡献比重和分布规律，根据流场特性和气动力特性给出气动外形局部优化设计建议，并归纳列车速度对气动力的影响规律。研究结果可为悬浮间隙、电磁力设置等提供基础数据，为气动外形优化设计提供参考，并为进一步研究列车运行安全性、舒适性等动力学性能提供参考依据。

1 数值计算模型

磁浮列车以600 km·h-1运行时马赫数为0.49，当马赫数大于0.3 时空气流动为可压缩流动［27］，因此采用可压缩模型模拟磁浮列车明线运行时的空气动力学问题。IDDES 方法在模拟列车空气动力学非定常特性方面有广泛应用。IDDES 是从延迟分离涡模型（DDES）发展而来，有效解决了DDES 在对数层曲线的不吻合问题；DDES 是从分离涡模型（DES）发展而来，通过引入延迟函数，有效解决了DES 中网格诱导分离问题［28］。DES 方法结合了大涡模型（LES）和雷诺平均纳维-斯托克斯湍流模型（RANS），在近壁面区域采用RANS方法，用雷诺平均的湍流模型模拟近壁面处小尺度的脉动运动；而在远离壁面的区域，用LES 方法模拟旋涡运动［29］。k-ωSST 湍流模型结合了k-ε和k-ω模型，在近壁面区域采用k-ω模型，在远离壁面区域采用k-ε模型，解决了k-ε和k-ω模型在流场求解中的缺点［28］。因此，本文采用基于k-ωSST 湍流模型的IDDES 方法，对磁浮列车明线稳定运行时的非定常流场和气动力进行数值模拟。

压力-速度场求解采用压力耦合方程组的半隐式方法（SIMPLE 算法），对流项采用二阶迎风格式，时间离散采用二阶隐式格式，使用代数多重网格（AMG）线性求解器求解动量、湍流方程。壁面处理采用STAR-CCM+软件中的高y+（第1 层网格质心至壁面的无量纲距离）方法。为严格遵守计算区域内网格上的库朗数（CFL）≤1，非定常时间步长取0.15 ms，每个求解步含20 次内迭代，连续性、动量和湍流方程的残差都小于10-6。计算时首先使用基于k-ωSST 湍流模型的RANS 方法进行定常流场稳态求解，得到的结果作为非定常流场的初始条件。然后使用IDDES 方法进行非定常流场计算，非定常求解时长设置为12.48 s，相当于空气流过4个计算区域通场的时间，空气从计算区域入口流到出口的时间即为1个通场时间。

1.1 列车和轨道模型

实际下线列车为5 车编组［30］，因此数值模拟中采用全尺寸5车编组模型，与实际列车编组数量一致。为准确模拟列车周围流场，列车模型尽量再现真实列车，减少简化，仅忽略车体外部的复杂细节，保留了风挡、车底滑橇等关键结构，几乎还原了真实的磁浮列车外形结构。选取车高h=4.20 m为特征尺寸，车宽b=0.88h，头尾车长6.69h，中间车长5.84h，相邻车厢用风挡连接，两相邻车间距为（风挡宽）0.06h，列车全长l=31.12h。车底等间隔布置滑橇，每节车厢底部共有8对滑橇，两相邻滑橇纵向间距为0.74h，横向距离为0.53h，纵向对称布置。时速600 km 磁浮列车空气动力学模型如图1所示。

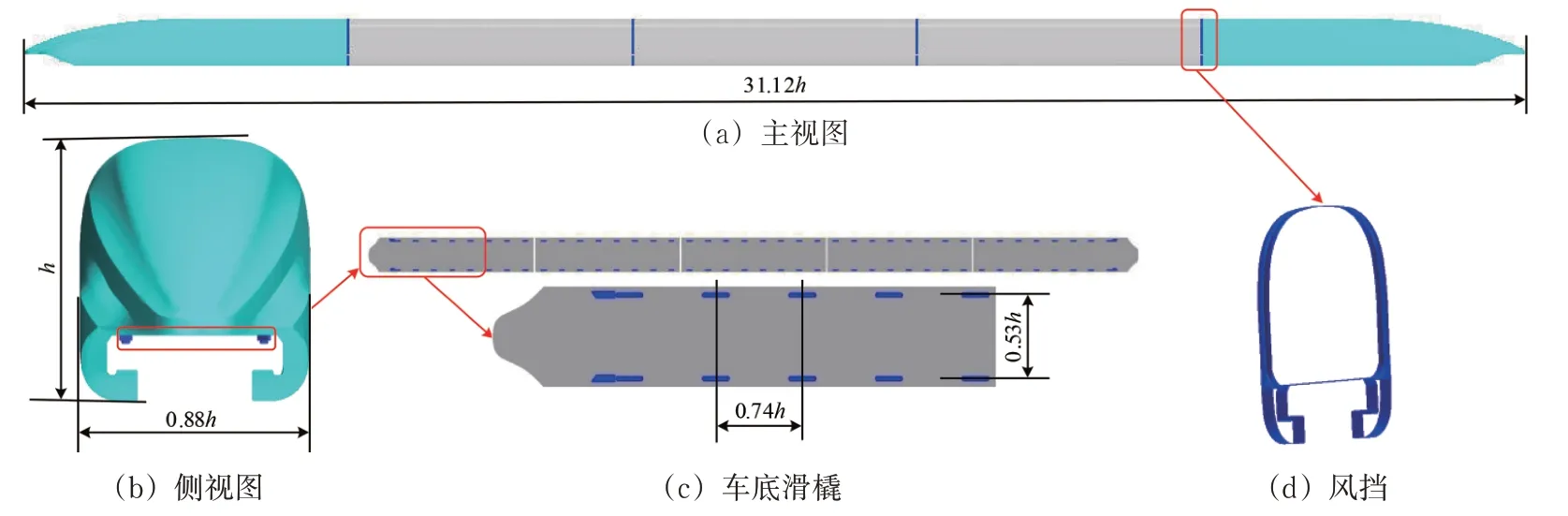
图1 时速600 km磁浮列车空气动力学模型

轨道采用时速600 km 高速磁浮列车的T 型轨道，如图2所示。

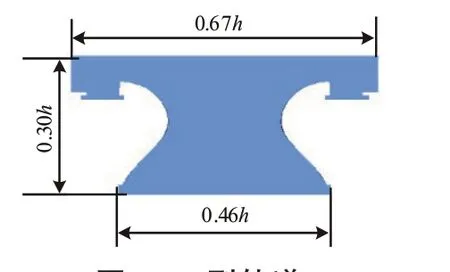
图2 T型轨道

1.2 计算区域和边界条件

计算区区域和边界条件如图3 所示，计算区域远场压力取101 325 Pa，温度为288 K。流入边界、流出边界、顶部和两侧面边界均为远场边界条件，用于模拟无穷远处的可压缩流动。车体为无滑移壁面边界条件。

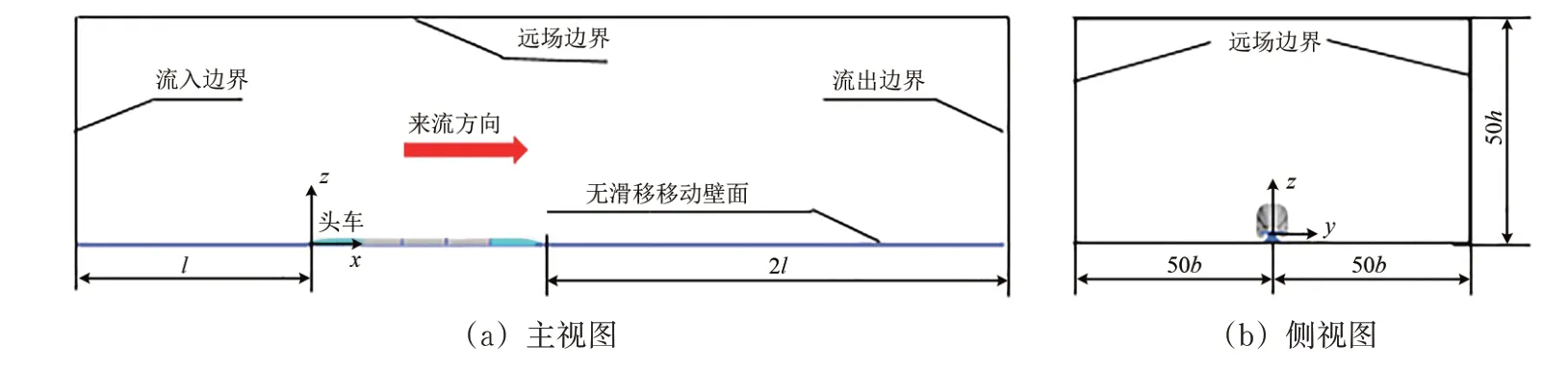
图3 计算区域示意图

磁浮列车贴地运行，地面效应对列车气动升力影响很大［31-32］，为模拟地面效应的影响，地面和轨道均设置为无滑移移动壁面，其移动速度与入口来流速度一致。为准确模拟边界层内的流动，并控制边界层内的网格数量，在列车、轨道和地面等壁面边界上采用标准壁面函数。计算区域坐标系原点位于车头鼻尖点和列车对称面x-z平面上，轨面位置处z=0，车底平面处z=0.15 m。

1.3 数据处理

为便于数据分析，对流场速度、压力和气动力进行无量纲化。根据CEN 标准［17］，速度系数Cv、压力系数Cp、阻力系数Cd和升力系数Cl分别为

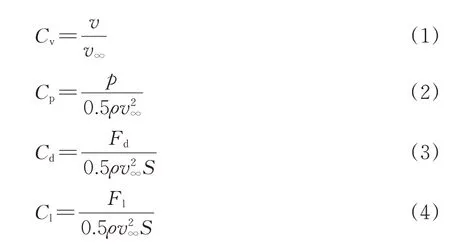
式中：v为流场速度；v∞为来流速度（列车运行速度）；p为压力；ρ为空气密度，取值1.225 kg·m-3；S为参考面积，取列车运行方向的横截面积12 m2；Fd和Fl分别为气动阻力和气动升力。

1.4 网格独立性验证

采用STAR-CCM+15.06软件进行网格划分，计算区域空间采用正交六面体非结构化网格，在近壁面区域拉伸边界层网格。考虑到列车底部、滑橇、风挡周围流场变化剧烈，对这些区域网格单独加密。车头和车尾周围流场变量梯度很大，因此对车头迎风区和车尾尾流区的网格也局部加密。列车底部与轨道间的悬浮间隙很小，流场变化复杂、剧烈，采用各项异性加密块进行网格的垂向（z轴方向）加密。列车附近至计算区域远场空间的流场变化逐渐减小，采用网格逐渐由密变疏、均匀过渡的网格密度控制方法，在车体周围设置3个互相嵌套的加密块。为了更准确地模拟空气在列车近壁面区域的流动，在车体、轨道和地面等区域拉伸边界层网格。

为研究网格密度对数值结果的影响，进行网格独立性验证工作，共划分3套网格，网格总数分别为5 000万、9 000万和12 000万个，分别称为粗糙网格、中等网格和精细网格。3 套网格划分思路一致，只是关键部位网格尺度大小和边界层网格层数存在差异，以中等网格为例展示数值模拟所用网格，如图4所示。

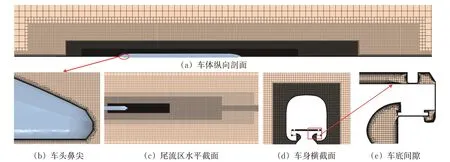
图4 中等网格示意图

车体表面y+取60，对应近壁面第1 层边界层厚度0.32 mm，车体表面y+分布云图如图5所示。

图5 车体表面y+分布云图

网格参数和不同网格下采用IDDES 方法数值模拟得到的列车气动力时间平均值见表1。从表1可知：网格密度对尾车升力的影响最大，以精细网格为基准，粗糙网格时尾车升力下降14.24%，中等网格时下降3.48%，中等网格与精细网格的气动力变化很小，证明选用中等网格密度就满足数值计算的精度要求；另外，考虑数值计算的效率要求，也应选用网格总数为9 000万个的中等网格。

表1 不同网格参数和气动力系数

1.5 计算方法验证

为验证所用计算方法的精准度和网格划分的合理性，通过与风洞试验的列车表面压力和气动力进行对比。在中国航空工业空气动力研究院截面为8 m×6 m 的风洞中进行试验，采用的列车模型为3车编组的1∶8 缩尺模型，且列车模型考虑了车底滑橇、风挡对列车气动性能的影响。风洞试验中来流雷诺数为2.8×106，侧偏角为0°，风洞试验模型与数值模拟模型对比如图6所示。

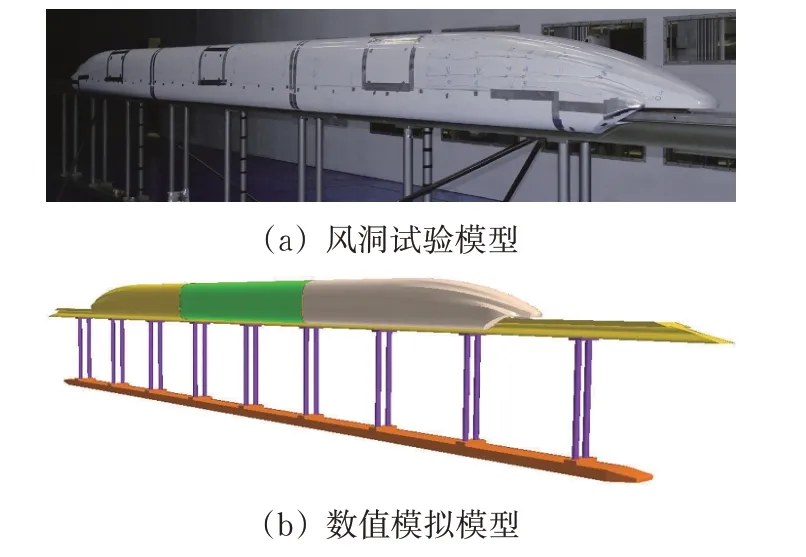
图6 模型对比

数值仿真与风洞试验［2］的车体纵剖面压力系数对比如图7所示。

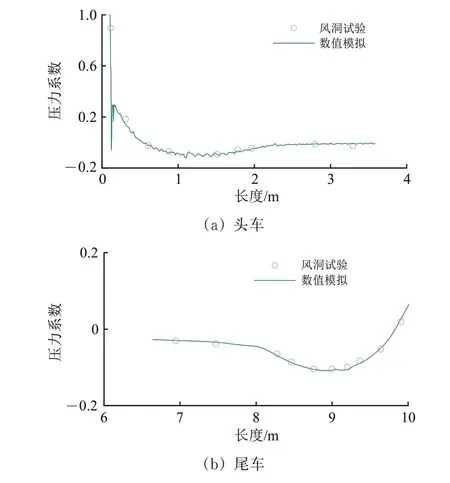
图7 列车纵剖面压力系数

从图7 可知：头尾车表面压力系数的数值仿真结果与试验结果基本一致，两者吻合较好，表明所采用的网格和计算方法能够准确模拟高速磁浮列车的车体表面压力。

将头车的气动升力无量纲化为1，其他气动力以此为基准进行无量纲化，得到风洞试验和数值模拟的气动力系数见表2。从表2 可知：数值模拟的误差较小，气动力最大误差为5.50%，在合理范围内，表明所采用的网格和计算方法同样能够准确模拟高速磁浮列车的气动力。

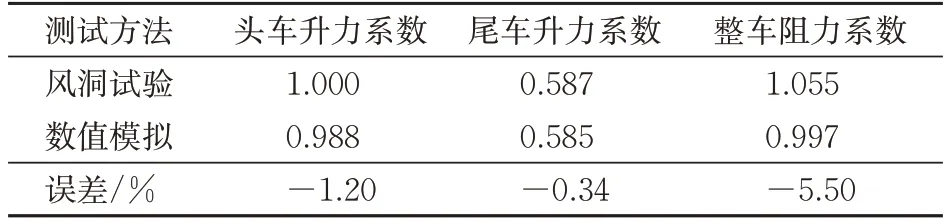
表2 风洞试验和数值模拟结果

综合风洞试验验证可知：本文采用的计算方法有足够的精度和准确性，可用于求解高速磁浮列车明线空气动力学问题。

2 流场结构

以车速600 km·h-1为例，对单车明线稳定运行时的非定常流场结构进行分析。

2.1 列车表面压力和速度流线

列车表面的时间平均压力云图如图8 所示，纵剖面的时间平均速度流线如图9 所示。从图8 和图9 可知：来流受到车头的阻挡作用，流速减小，车头前方空气受到挤压作用导致车头前方的压力增大，在车头鼻尖处产生强高压区，在设备舱导流区也产生强高压区，在导流区后的车体底部产生强负压区；在司机室上方，空气流速增大，大于来流速度，导致该区域产生较强负压；在车身平直段顶部和两侧区域，空气向后流动，处于微小的负压状态；在尾车司机室上方，空气流速增大，形成负压区；在尾车鼻尖处，空气流速急剧减小，形成正压区；头车与尾车的压力分布规律相似，但头车流线段的压力幅值比尾车的大。

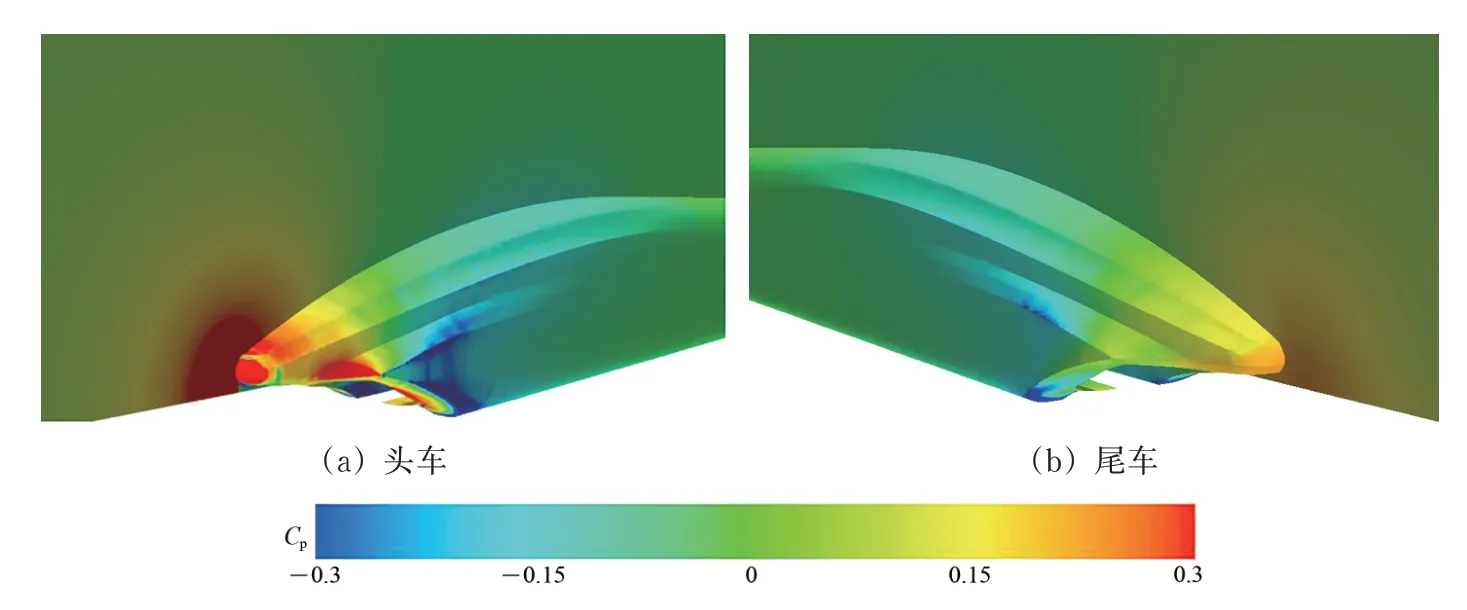
图8 列车表面压力云图

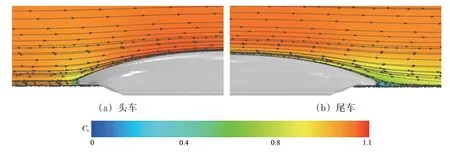
图9 纵向对称面速度流线

垂向截面z=0.075 m（垂向方向上悬浮间隙中间位置，距离轨面0.075 m）处的时间平均压力云图如图10 所示，时间平均速度流线如图11 所示。从图10 和图11 可知：在头尾车鼻尖下方，气流速度减小，形成正压区，车头鼻尖的正压比车尾的大；滑橇前后端存在正负压区，越接近车尾，正负压越小；在头尾车鼻尖下方，悬浮间隙内的气流速度也发生突变，速度急剧减小；从车头到车尾方向，车身平直段悬浮间隙内的气流速度呈减小趋势。

图10 悬浮间隙内的压力云图

图11 悬浮间隙内的速度流线

列车纵剖面的时间平均压力分布曲线如图12所示。从图12 可知：头尾车流线段的压力变化非常剧烈，车身平直段顶部的压力几乎没有变化，压力接近于零；车身平直段车底压力呈等间距波动，越接近车尾，波动幅值越小；车身平直段上表面的压力接近于0、下表面为正压；在车头鼻尖位置，上表面正压较强，下表面负压较强；从尾车流线段开始，上表面的压力减小，下表面的压力几乎不变；在尾车司机室区域，上表面的压力开始增大，下表面的压力也呈增大状态，上表面的压力增大速度比下表面的快。磁浮列车的气动升力主要是由车体上下表面的压力所决定的，由于特殊的“抱轨”运行方式，地面效应显著，高速运行时车底空气受压缩，产生吸管效应，底部呈正压；上表面绝大部分压力为微小的负压或接近于0，车底压力对列车升力起主导作用，导致列车绝大部分区域受到垂直向上的升力作用，这是和轮轨列车所不同的。

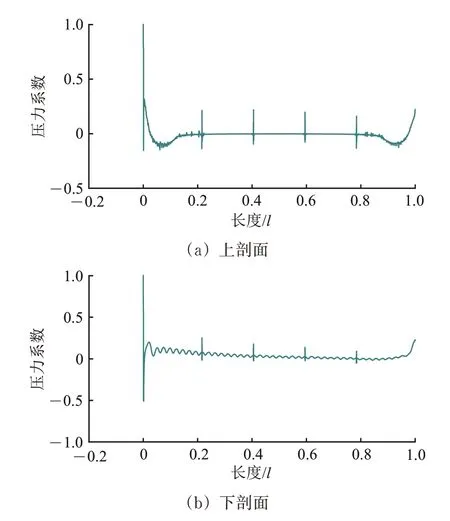
图12 车体纵剖面压力

2.2 列车周围旋涡结构

列车周围流场的非定常特性可通过不同时刻的流场结构展示出来，由于篇幅限制，取距离车尾鼻尖4h处1个横截面的流线图，如图13所示。图中：图（a）为定常流动模拟结果，其他图为非定常流动不同时刻模拟结果；红色字母表示的是不同的旋涡。从图13 可知：非定常流动各个时刻的流线趋势与定常流动总体是一致的，但在流场细部结构上存在较为明显的差异，采用IDDES 方法得到的流场信息比采用RANS 方法的要详细得多。非定常流动各个时刻尾流区旋涡的几何尺度和位置均发生变化，数量也发生改变，2 种流场结构的差异逐步增大；在整个时间非定常流动过程中始终存在着纵向对称的大尺度主旋涡A 和主旋涡B，但其形状、尺度和位置都随时间而变化；旋涡C、旋涡D 和旋涡E不断呈现出形成、破碎、再形成的状态，并在破碎时伴生出附加的小尺度旋涡。综上，在尾流区存在许多强度不同、空间几何尺度各异并随时间变化的旋涡，它们不断从车体产生、脱落、附着、分离和合并，并向下游运动，涡的分离具有明显的随机性和脉动性，这是列车气动力发生非定常波动的主要原因。

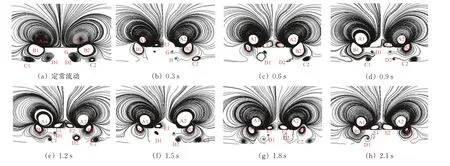
图13 列车尾流区横截面定常流动和不同时刻非定常流动的流线

采用Q准则识别列车周围的旋涡结构，Q准则表达式为［33］

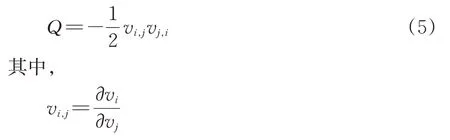
式中：i和j是笛卡尔坐标系的坐标轴方向；vi和vj是笛卡尔坐标系下的速度分量；vi,j和vj,i是速度梯度张量；Q是速度梯度张量的第二不变量。

列车周围的定常流动（RANS）和非定常流动（IDDES）的瞬时旋涡结构（Q=100 s-2）如图14所示。图中：用时间平均速度云图填充，由于篇幅限制，非定常流动只给出1个瞬时的结果。从图14可知：在车体周围，定常流动与非定常流动的瞬时旋涡结构和旋涡尺度几乎一致。但在尾流区，2 种模拟方法得到的旋涡结构有明显的差异，采用IDDES 方法获得的流场信息详细的多。列车周围的旋涡主要分布在头尾车流线段和尾流区，风挡处旋涡结构也较多，车身平直段旋涡相对较少，尺度也较小；平直段的速度幅值较头尾车流线段的低，流线段与平直段过渡处速度幅值很大；在头车流线段2 侧各脱落出4 个尺度较大的旋涡，并沿车身向后发展，接近车顶的旋涡在头车平直车身位置消失，侧墙中间的2 个旋涡在第1 个风挡位置消失，接近车底的旋涡一直延伸到第3节车位置消失；在头尾车流线段顶部，旋涡呈条状分布，但尾车的速度幅值比头车的低；在尾流区，尾车流线段2 侧各脱落处3 个尺度较大的旋涡；在尾车设备舱导流区域、轨道2 侧底部区域和车尾鼻尖处，各脱落出2 个纵向对称分布、尺度较大的旋涡。不同流动情况下，尾流区同一旋涡的尺度相当，但旋涡形状有明显区别。定常流动时的各个旋涡呈直线状向后发展，各个旋涡之间没有干涉和合并等相互作用；非定常流动时，车尾脱落出的所有旋涡向后发展的过程中在尾流区发生相互作用，不同旋涡呈“缠绕”状，向后发展过程中存在旋涡脱落、附着、分离和合并；轨道底部2侧的旋涡呈螺旋状向后发展。

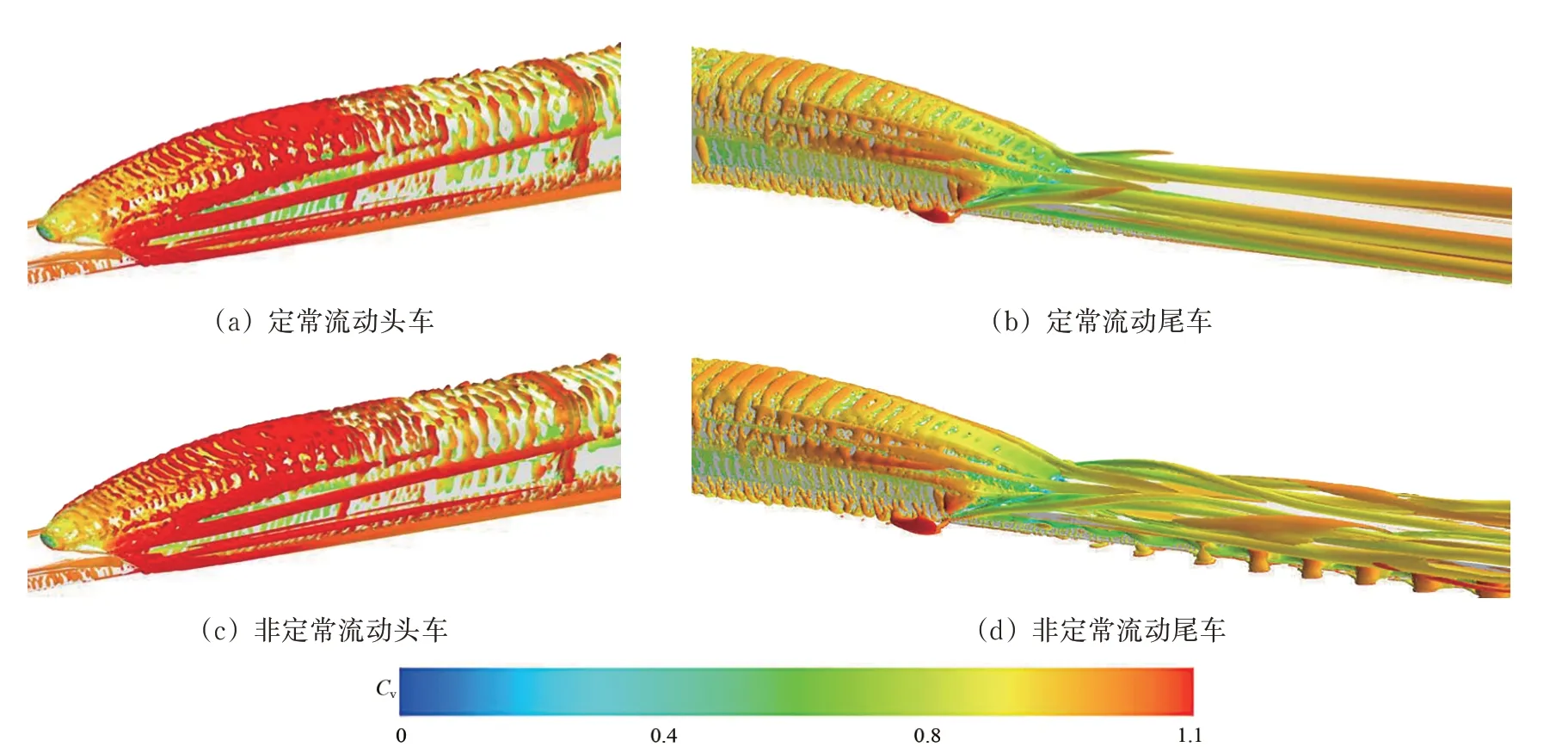
图14 列车周围旋涡结构

3 列车气动力

以车速600 km·h-1为例，对单车明线稳定运行时的非定常气动力的时域特性和频域特性进行分析，得到气动力随时间变化规律和气动力功率谱密度峰值频率与车辆系统固有振动频率之间的关系，有助于对列车的气动安全性进行深入分析，为气动外形优化提供依据。

3.1 气动力时域特性

用IDDES 模拟可得气动系数时间历程曲线，由于篇幅限制，只给出头车、3 车和尾车的气动力时间历程曲线如图15 所示。图中：红色直线为t=3 s后的时均值，模拟结果显示t=3 s之后，气动力在时均值上下准周期性波动，流场充分发展，因此取t=3 s 之后的数据进行分析，并取数据平均值作为时均值。从图15 可知：磁浮列车明线高速运行时，各节车气动力存在明显的非定常特性，但均在时均值上下准周期性波动；从头车至尾车，各节车升力波动幅度总体呈增大趋势，尾车升力最大波动幅度（最大波动幅值与时均值的比值）为12.48%，尾车升力的波动幅度远大于其他车。

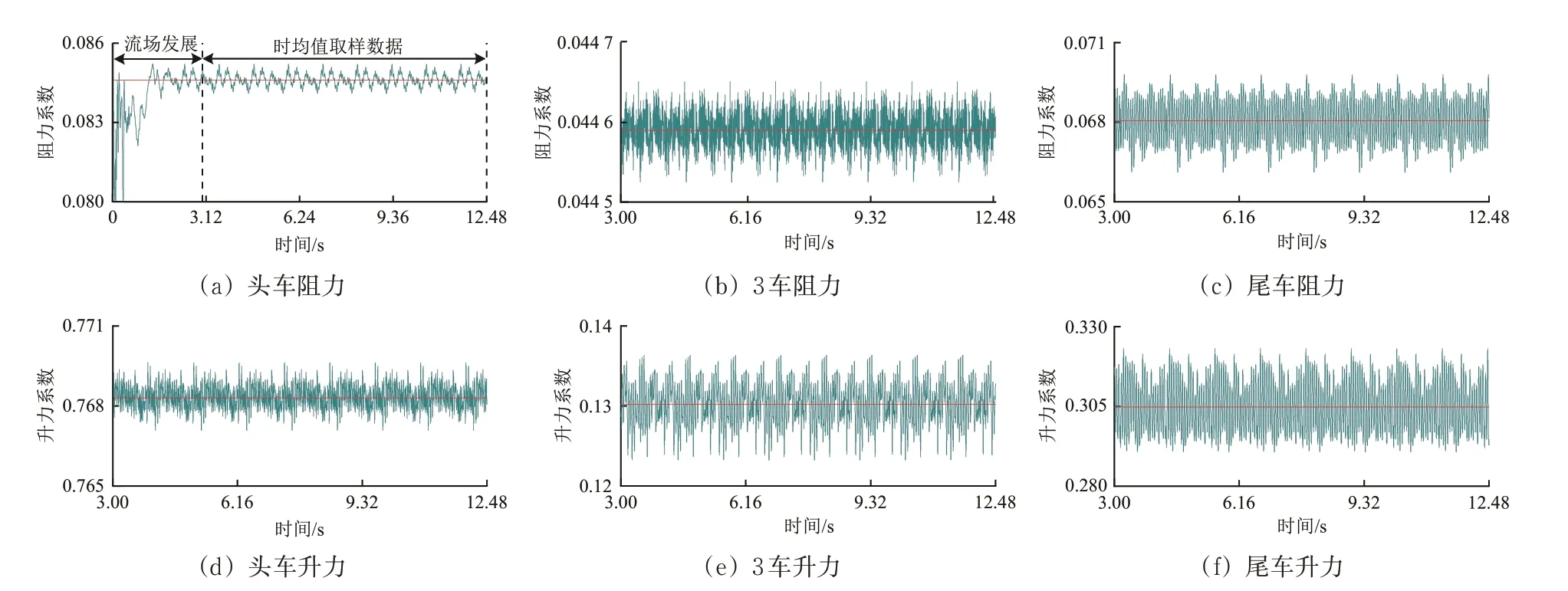
图15 气动力系数时间历程曲线

为分析非定常流动对气动力的影响，定常（RANS）和非定常（IDDES）模拟得到的气动力对比结果见表3。表中：各节车不包含风挡。从表3 可知：定常模拟和非定常模拟的气动力结果大体一致，但存在小的差值，气动阻力差值很小，最大差值为2.6%（以非定常为基准），气动升力差值相对较大，尾车气动升力差值达7.65%，但所有气动力差值在10%以内；头车的气动升力远远大于其他车，过大的气动升力对列车悬浮系统提出更高要求，严重时会导致列车悬浮系统失效，对列车运行安全性和稳定性造成影响［2］；对于中间平直车厢，越接近车尾各节车升力越小，但各节车的升力均为正值。

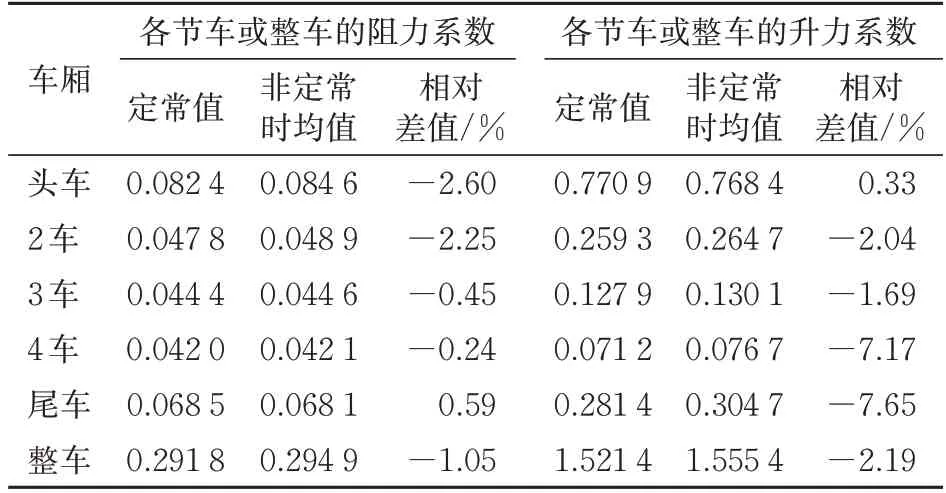
表3 定常和非定常模拟气动力系数比较

磁浮列车无轮轨支撑作用，列车悬浮依靠电磁力，当列车的悬浮高度因外力发生频繁变动时，悬浮电磁力也随之改变来抵消这一外力。由于悬浮电磁力变化与外力变化存在时间差，导致车辆发生垂向振动，严重影响旅客舒适性并有害于电磁悬浮系统，严重时会损坏悬浮系统［23］。正升力影响列车运行稳定性，负升力增加悬浮能耗，因此应尽量减小升力及其脉动。对于磁浮列车，理想的情况是列车升力为0且无波动。由于列车升力主要是由车体上下表面的压力决定，而车底压力主要是由悬浮间隙内的流场特性所决定［3］，因此可通过改变头尾车车底外形、悬浮间隙或加装导流装置［3］改变车底空气流动特性，减小列车升力及其波动幅度。

3.2 升力频域特性

为分析磁浮列车气动力的周期变化规律和波动幅度，对气动力的频域特性进行分析。非定常气动力的频域特性可通过对气动力时域信号进行傅里叶变换得到。由于阻力波动对列车运行安全性等几乎没影响，只对气动升力的频域特性进行分析。气动升力频域特性分析中，为了直观给出气动升力的振动强度，直接给出气动升力功率谱密度的频谱曲线。

各节车气动升力功率谱密度幅值和频率的关系如图16 所示。从图16 可知：各节车气动升力功率谱密度的频率范围、最大峰值频率几乎一致，主要分布在0～20 Hz 频率范围内，最大峰值频率为9.3 Hz 左右；从头车至尾车，各节车升力功率谱密度的最大峰值呈增大趋势，尾车升力的最大功率谱密度峰值为1.7 kN2·Hz-1，对应频率为9.3 Hz。

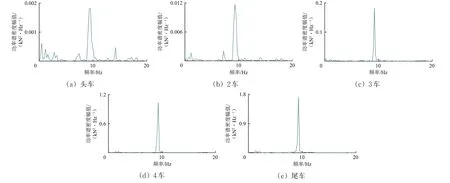
图16 气动升力功率谱

功率谱表征了气动力振动能量与频率的关系，功率谱密度幅值越大，气动力振动能量越大，因此尾车的稳定性相对越差。若气动力功率谱密度的最大峰值频率与车辆系统固有频率耦合，则会使车体失稳。由文献［34］可知：时速600 km 磁浮列车悬浮架和车尾电磁铁的垂向自振频率在28 Hz 以上，气动升力功率谱密度的最大峰值频率在车辆系统固有振动频率之外，不会产生共振，避免了因共振而增强车体的垂向振动。

3.3 关键部件阻力分布特性

列车关键部件阻力系数见表4。表中：阻力系数为IDDES 方法模拟的时间平均值。从表4 可知：头尾车流线段存在形状阻力，特别是尾车流线段、滑橇和风挡的形状阻力占比相对较大；整车形状阻力仅占21.5%，远小于摩擦阻力，摩擦阻力占主导地位。

表4 列车各部位阻力系数

通过改变车头外形大幅度减小列车气动阻力已经趋于极致。若要大幅度减小列车的气动阻力，可考虑应用非光滑表面减阻技术或者表面抽吸气法等边界层控制减阻技术来减小列车的摩擦阻力，进而达到减小列车气动阻力的目的［35］。建议对风挡、滑橇进行气动外形优化，减小其形状阻力。在满足制造工艺等条件下，风挡外形可参考我国高速列车全封闭结构形式［36-37］；滑橇可设置为伸缩结构，列车悬浮运行后，将滑橇收起来，直接消除滑橇的影响。

3.4 车速对气动力影响特性

车速400～660 km·h-1下各节车的气动力系数定常模拟值见表5。从表5 可知：不同车速下各节车的气动力系数基本保持不变，根据力系数定义，列车气动力与车速的平方近似成正比关系，阻力与车速的关系符合Davis公式理论［38］。

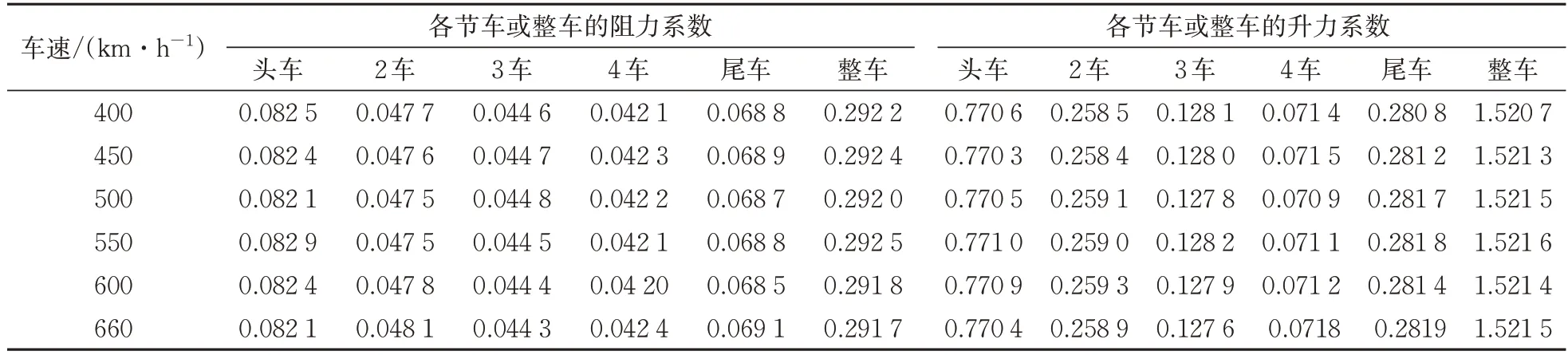
表5 不同车速下的气动力系数

4 结论

（1）明线稳定运行时，列车周围流场和气动力都呈现出明显的非定常特性，非定常气动力在时均值上下准周期性波动；阻力的波动幅度较小，升力的波动幅度相对较大；从头车到尾车，升力波动幅度呈增大趋势，尾车升力最大波动幅度为12.48%；在车头和车身平直段周围，瞬态模拟与定常模拟的流场旋涡结构几乎一致，但在尾流区2 种模拟的旋涡结构有明显区别；气动力时均值和定常值大体一致，但存在小的差值；气动阻力差值很小，最大差值为2.60%，气动升力差值相对较大，尾车气动升力差值达7.65%。

（2）各节车升力功率谱密度的频率范围、最大峰值频率几乎一致，主要在0～20 Hz 频率范围内，最大峰值频率为9.3 Hz。从头车到尾车，升力功率谱密度最大峰值呈增大趋势，即尾车升力波动强度最大。

（3）头车气动升力远大于其他车，尾车次之，可考虑通过改变列车底部外形或加装导流装置来改变列车底部的空气流动特性，进而减小头尾车的升力和波动幅度。

（4）整车摩擦阻力占列车总气动阻力的78.50%，占主导地位。若要大幅度减小列车气动阻力，可考虑应用非光滑表面等技术减小摩擦阻力。

（5）以400～600 km·h-1速度等级明线稳定运行时，气动阻力和升力与车速平方成正比，高速运行时升力问题是磁浮列车的关键空气动力学问题。

（6）头尾车设备舱导流区域、风挡和滑橇存在压力突变，气动外形优化时建议优化。