汽车电子节气门系统自适应固定时间预设性能控制
万春雨 ,焦晓红 ,王 众
(1.燕山大学电气工程学院,河北秦皇岛 066004;2.燕山大学车辆与能源学院,河北秦皇岛 066004)
1 引言
电子节气门是汽车发动机控制系统重要的组成部件,其位置跟踪性能直接影响汽车驾驶安全性、动力性、燃油经济性[1–2].电子节气门系统具有典型的非线性特征,并且存在系统物理参数的不确定性.这些形成了电子节气门系统具有挑战性的高性能控制要求.
许多控制方法被应用于汽车电子节气门控制设计.例如:针对电子节气门系统非线性问题,文献[3]基于Backstepping递归法设计了非线性位置跟踪控制器.针对参数不确定问题,文献[4–5]采用了基于粒子群优化算法辨识节气门系统模型设计伺服控制的策略,文献[6–13]则采用了各种鲁棒自适应控制技术处理不确定性.滑模动态对系统不确定性完全鲁棒的特质使得滑模控制技术被广泛应用;从设计的控制策略在实际系统上实施具有泛化性讲,具有在线估计能力的自适应技术较受青睐.于是,更多的滑模控制与自适应技术结合的控制策略被实施在汽车电子节气门系统上,如,文献[6–7]利用线性滑模面设计了节气门自适应滑模控制器.但抖振现象是滑模控制的本质弱点,为此各种减抖的滑模控制被应用,如,积分终端滑模[8]、自适应动态滑模[9]和非奇异终端滑模[10].另外,基于自适应非线性Backstepping设计方法的各种控制策略也被应用于节气门系统,如,文献[11]设计了保证节气门开度跟踪误差渐近收敛的自适应非线性控制器;文献[12]设计了自适应有限时间伺服控制,通过有限时间收敛提高位置跟踪的暂态性能;文献[13]设计了基于障碍Lyapunov函数与Backstepping方法的自适应控制器,实现满足节气门非对称节流角约束下的位置跟踪.尽管这些控制策略实现了电子节气门位置跟踪控制系统暂稳态性能的逐步提升,但都还有不同方面不同程度的进一步改进系统控制性能的空间.
近些年针对非线性系统提出了一种预设性能控制方法,通过设计预设性能函数保证系统被控量的暂稳态性能达到满意的要求[14–15].这种预设性能控制方法很快被应用于各种工程控制设计中,如,汽车电子节气门系统[16]、飞行攻角伺服系统[17]、板球系统[18]、船舶直流微电网系统[19].值得提及的是,传统的预设性能函数选取依赖于指数函数,理论上动态过程是渐近收敛的.为此,文献[20]针对不确定非线性系统设计了预设性能有限时间控制器,使得系统跟踪误差在有限时间内收敛到预定义界内.然而,有限时间收敛是依赖于系统初始条件的.因此,Polyakov首次提出的固定时间稳定性理论[21]更适宜工程实际应用,其固定收敛时间不依赖于系统初始条件.目前,已有将固定时间稳定性理论融入各种控制策略设计中的研究,例如,文献[22]将固定时间收敛性与滑模控制相结合,针对描述为拉格朗日形的机械系统设计了固定时间自适应滑模控制.文献[23]将固定时间收敛概念引入预设性能函数设定中,针对一类二阶非线性系统提出了一种预设性能固定时间跟踪控制方法.
基于以上分析,本文欲将预设性能控制策略和固定时间稳定性理论及自适应技术结合起来,设计一种自适应固定时间预设性能控制策略,应用到汽车电子节气门控制系统中,较好地提高实际中节气门开度轨迹跟踪的暂稳态性能.与现有相关文献的区别在于:在控制器设计推导中,充分考虑各种实际工况产生的误差系统初始条件和物理限制条件,将其结合到控制器的预设性能函数参数的选取中,性能函数选取具有预设固定时间的形式,同时使用固定时间稳定性理论替代Lyapunov渐近稳定性理论推导控制器,得到不依赖于系统初始条件的固定收敛时间,保证控制系统在实际运行中具有更高的暂态性能.在控制策略有效性和优越性验证中,用于验证的运行工况不仅包含能展示控制策略提高暂稳态性能有效性的一些极限工况,还给出了实际汽车运行中电子节气门真实开度轨迹的情况验证.
2 汽车电子节气门控制系统
汽车电子节气门系统包括节气门体和电子控制单元(electronic control unit,ECU),节气门体由位置传感器、直流电机、减速齿轮组、节气门阀片和反向弹簧集成,其系统结构控制原理如图1所示.当综合了当前路况、车速等因素的驾驶意图信息通过位置传感器传递给ECU时,ECU得到希望的节气门开度信号,同时也收集了节气门位置传感器反馈的当前开度信号,通过控制算法处理这些信号并发出PWM电压信号,使电机通过反向弹簧和齿轮传动将阀片翻转到其一定的开度位置,至此实现了节气门系统的闭环控制.
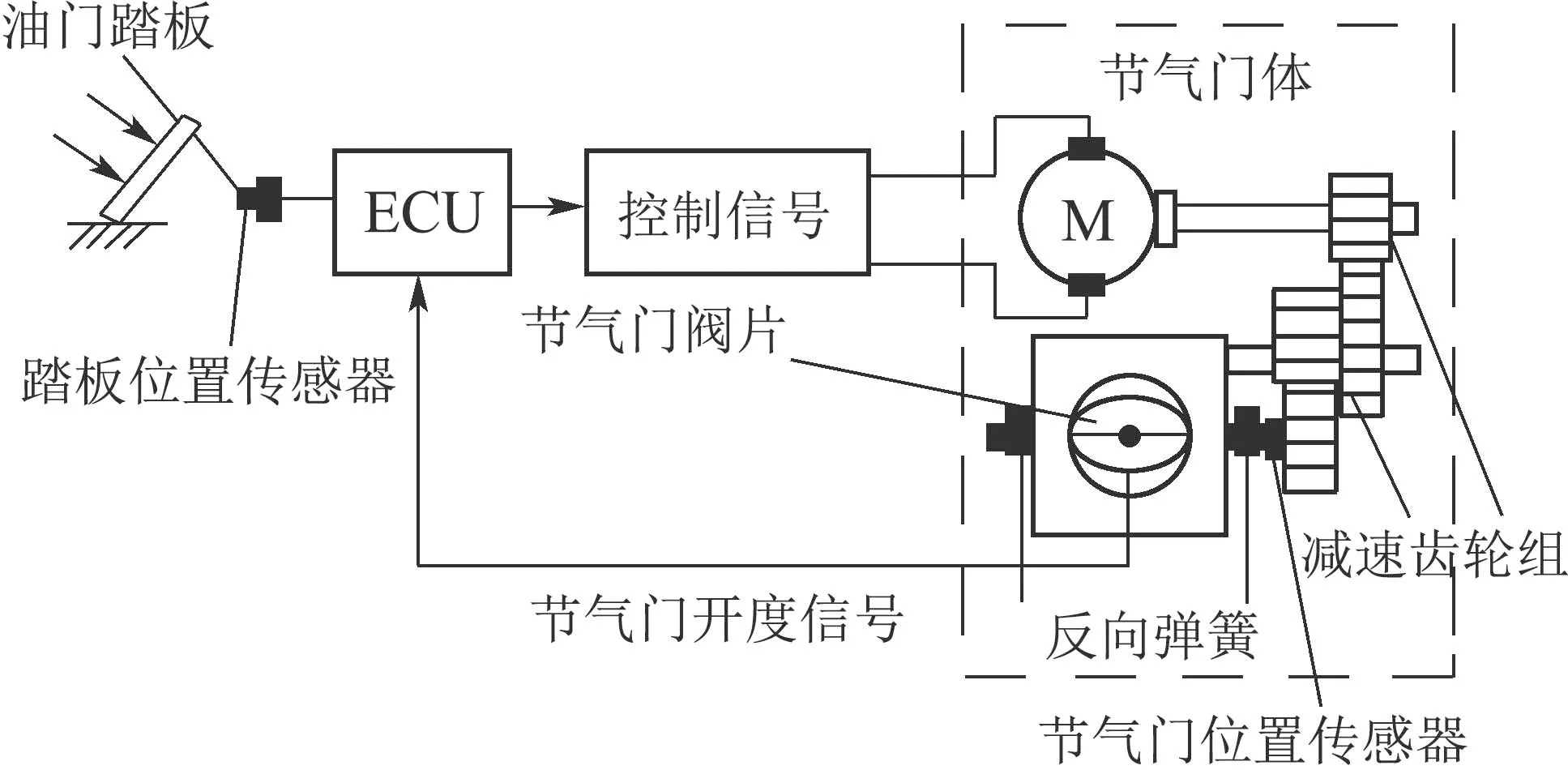
图1 电子节气门系统结构控制原理图Fig.1 Schematic of the electronic throttle control system
根据电子节气门的机电特性,系统动力学方程为
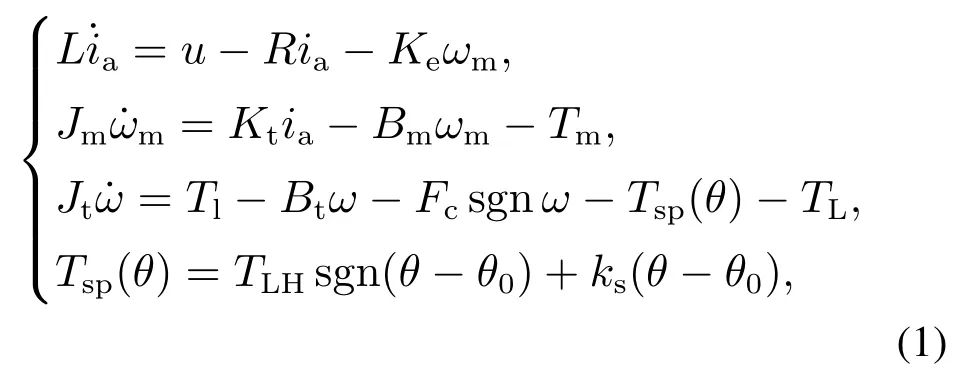
式中:u为电机控制输入电压;ia,R和L分别为电机电枢电流、电阻和电感;ωm和ω=分别为电机和阀片角速度;Ke为电动势常数;Kt为电机转矩常数;θ为节气门阀片开度;Jm/Jt和Bm/Bt分别为电机轴侧/阀片侧的转动惯量和粘性摩擦系数;TL为负载转矩,包括气流力作用在阀片上引起的扰动转矩;Tm和Tl分别为电机轴负载转矩和齿轮组输出转矩;Fc为库伦摩擦系数;TLH为弹簧偏移系数;ks为弹簧弹性系数;θ0为节气门的默认开度.
实际系统中控制输入电压具有饱和约束,描述为

式中:umax,umin是已知的界值.同时由于实际的电机电枢电感L值非常小,电流动态特性可以忽略,所以电子节气门系统的动态模型为

由于存在电子节气门元器件制作工艺不同、物理参数未知、以及设备老化等问题,使得节气门系统的实际物理参数L,R,ks,J,B,Kt,Ke,n,Fc,TLH,TL都存在着不确定性,从而系统(3)中a1,a2,a3,c1,c2,b,均具有不确定性.
汽车电子节气门控制系统的性能要求如下[4]:
1) 在任何运行工况和参考信号变化条件下,节气门阀片开度的调节时间(阀片开度达到并保持在稳态值5%的误差范围内的最小时间)要求小于100 ms.
2) 阶跃响应条件下几乎没有超调产生,即节气门阀片在运动过程中不会与最大开度时的节气门机械结构发生碰撞.
3) 系统的稳态跟踪误差均值小于0.11◦,且动态跟踪误差不超过7◦.
4) 控制器输出符合实际应用中对系统控制输入的物理限制条件.
为了叙述清晰,本文设计的控制系统稳定性与收敛性分析所需要的引理列出如下.
引理1假设如下系统对于所有初始条件x0,在正向时间内均有唯一解
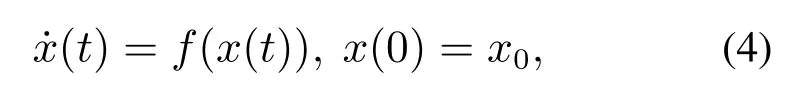
其中:x ∈Rn,f(x):U0→Rn在原点开邻域U0内是连续的,且f(0)=0.如果存在一个正定Lyapunov函数V(x):Rn →R,并且有[24]
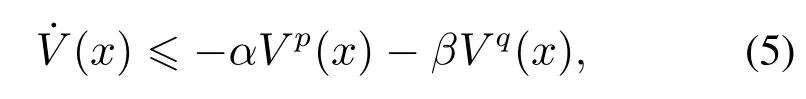
则系统(4)是全局固定时间稳定的,且稳定时间满足

其中0 引理3对任意实数xi(i=1,2,···,n),p>1,有下列不等式成立[25]: 为了提高实际节气门开度轨迹跟踪暂稳态性能,本节将预设性能控制与固定时间稳定性理论相结合,通过自适应技术设计一种自适应固定时间预设性能控制策略,保证闭环控制系统节气门开度位置跟踪高性能及对运行过程中参数变化和负载扰动的鲁棒性. 首先是预设性能函数的设计:充分考虑各种实际工况产生的误差系统初始条件和物理限制条件,将其结合到预设性能函数参数的选取中,且性能函数选取具有预设固定时间的形式 式中:ρ0,ρT0,λ,τ >0为预定义设计参数,且τ=,m和n分别为任意正奇数和正偶数.根据实际节气门系统默认角度一般12◦左右,最大角度为90◦,转换为弧度制,并考虑快速性能要求,则定义预设性能参数为:ρ0=1.57,ρT0=0.02,λ=20,τ=4/5. 依据预设性能控制设计原则,定义转换误差函数 保证−δ1<ψ(ε(t))<δ2,其中δ1,δ2>0是设计参数,e(t)=θr(t)−θ(t)是跟踪误差,则虚拟误差为 进而,有如下的命题. 命题1针对带有参数不确定性和饱和约束的电子节气门系统(12),如果设计一种如下形式的自适应固定时间预设性能控制器: 其中η是针对控制输入饱和问题引入的辅助设计变量 注1需要指出的的是:控制器(13)–(15)的设计过程并不是简单地将文献[12]中的自适应有限时间控制器设计和文献[16]的自适应预设性能控制器设计结合起来.与文献[12]相比:除了加入预设性能控制框架的明显不同外,还采用了不依赖初始条件的固定时间收敛理论替代了有限时间稳定性理论设计控制器.与文献[16]相比:尽管都是预设性能控制设计框架,但是具有固定时间收敛的预设性能函数替代了传统的指数渐近收敛预设性能函数,且固定时间稳定性递归推导替代了传统的渐近稳定性Backstepping递归设计,更主要的不同是将可改善跟踪性能的内模原理方法与基于预设性能函数的误差转换相结合.另外,为了实现闭环系统的固定时间稳定,对处理控制输入饱和问题引入的辅助变量的动态方程也进行了改进. 命题成立分析是在基于Backstepping递归设计的框架下进行的,主要的步骤如下: 首先,针对系统(12)子系统ξ选择Lyapunov函数 在坐标变换z2=ε −α1及虚拟控制α1的设计下,其时间导数满足如下等式: 其次,针对系统子系统(ξ,ε)构造Lyapunov函数 再次,针对系统(12)及考虑处理饱和引入的辅助变量η,构造Lyapunov函数 则直接计算其时间导数并考虑式(14),有如下等式: 因此,根据Lyapunov稳定性理论及LaSalle不变集原理,可知闭环系统所有信号ξ,z2,z3,η,有界,且ξ,z2,z3,η收敛为0,进而根据微分同胚的坐标变换可得ε,e,x3收敛为0. 接下来分析ξ,z2,z3,η不受初始条件ξ(0),z2(0),z3(0),η(0)限制以固定时间收敛为0.重新审查不等式(21),定义 由于闭环系统所有信号有界,则一定存在一个正常数λ使得|F|≤λ,并注意到b>1,因此不等式(21)满足下式: 因此,对任意参考节气门开度信号及存在系统参数不确定性及外部干扰情况下,闭环系统(12)–(15)都能保证跟踪误差均在具有固定时间收敛的预定义性能界内,并且跟踪误差快速收敛(θ →θr,∀t≥T)的动态性能不受其初始条件的限制. 为了充分验证本文提出的控制策略的控制性能,选取如下2种运行工况,在MATLAB/Simulink环境下进行仿真验证. 工况1节气门期望输出信号为开度增加和减小不同幅值变化的阶跃信号,验证在不同的快速加减速运行状态下气门开度跟踪响应的暂稳态性能. 工况2节气门期望输出信号为通过θ0位置的变化较小的阶跃信号,目的是验证所设计控制器克服反向弹簧等非线性特性的性能.因为在实际怠速或极低速行驶情况下(为θ0附近的节气门小角度变化),位置跟踪性能受反向弹簧等非线性作用的影响更大. 运行工况中同时考虑了系统存在负载干扰TL=0.1 sin(2πt)[Nm]和10%的参数摄动不确定性.仿真中采用的电子节气门系统模型参数来源于2009IFAC专题ECOSM公布的挑战问题[26],见表1. 表1 电子节气门系统物理参数Table 1 Parameters of electronic throttle system 仿真中控制参数及自适应估计参数的初值选择为 两种仿真工况下的结果如图2–3所示,同时表2总结了两种工况下的系统性能指标. 图2 仿真工况1下系统输出和控制输入响应Fig.2 Output and control input of ETS in simulation case 1 图3 仿真工况2下系统输出和控制输入响应Fig.3 Output and control input of ETS in simulation case 2 图2–3和表2表明:当节气门系统在不同工况运行下,系统输出跟踪误差响应曲线总是在性能函数的界内(图中的上下限曲线),动态性能均没有超调、调整时间35 ms到75 ms,稳态误差几乎为零.因此,仿真结果表明所设计的控制器能够保证闭环系统对任意参考位置信号的高性能跟踪. 表2 2种工况下系统性能指标Table 2 System performance index in two cases 为了证明本文设计的自适应固定时间预设性能控制器(adaptive prescribed performance fixed-time control,APPFTC)在提高跟踪暂稳态性能上的优势,与现有研究成果进行对比验证.选取参考文献[12]中的自适应有限时间伺服控制器(adaptive finite-time servo control,AFTSC)和参考文献[16]中的自适应预设性能伺服控制器(adaptiveprescribedperformanceservocontrol,APPSC)进行仿真比较,仿真结果如图4–5所示. 图4 本文的APPFTC和文献[12]的AFTSC仿真对比Fig.4 APPFTC and AFTSC simulation comparison 图5 本文的APPFTC和文献[16]的APPSC仿真对比Fig.5 APPFTC and APPSC simulation comparison 通过图4–5可以看出,本文设计的控制器在控制系统的响应速度和稳态误差方面都有一定的改进,显示了其进一步改善系统的暂稳态性能上的优越性.但是可以看到采用预设性能控制(APPFTC和APPSC)的控制输入电压u在系统动态过程具有振荡现象,主要原因在于饱和特性前的控制器输出v在动态调整过程中具有非常大的增益.预设性能控制的高增益现象在本文的设计方法中并未得到解决. 通过仿真可在极限运行工况对控制器性能进行验证,而实验则能更真实的反映实际运行情况.因此,选取如下工况进行基于dSPACE的硬件在环实验验证. 工况1节气门期望输出信号为短时的一个恒定的开度角,为了明显显示系统响应的动态性能. 工况2节气门期望输出信号为开度增加和减小不同幅值变化的阶跃信号,验证在不同的快速加减速运行状态下气门开度跟踪响应的暂稳态性能. 工况3节气门期望输出信号为根据实际车速生成的开度信号[2],验证控制器的实际性能. 需指出的是,由于实际的电子节气门与仿真中的不同,实验运行中控制器参数的选择也不尽相同,选取的不同控制参数为 3种实验工况的实验结果见图6–8.实验结果表明,本文提出的控制策略运行在不同的工作条件下均可以使电子节气门阀片快速准确地跟踪期望信号,满足控制系统性能要求. 图6 实验工况1下的系统输出与控制输入Fig.6 Output and control input of ETS in experiment case 1 图7 实验工况2下的系统输出与控制输入Fig.7 Output and control input of ETS in experiment case 2 图8 实验工况3下的系统输出与控制输入Fig.8 Output and control input of ETS in experiment case 3 为了进一步证明本文设计的APPFTC优越性,与参考文献[16]中设计的APPSC进行实验对比,实验结果如图9所示.实验对比得到与仿真对比相同的结论:本文所设计的控制器在系统暂稳态性能方面的控制效果更佳,但预设性能控制易产生的控制输入高增益现象没有得到解决. 图9 本文的APPFTC和文献[16]的APPSC实验对比Fig.9 APPFTC and APPSC experiment comparison 本文设计并应用了汽车电子节气门系统的自适应固定时间预设性能控制器,仿真和实验结果均表明,所设计控制器克服了系统的非线性和参数不确定性,可保证节气门开度跟踪动态性能无超调、调整时间快,稳态跟踪误差几乎为零.证明了所设计控制器进一步增强了控制系统对不同运行工况和环境变化的适应能力.但尽管设计中考虑了饱和特性,控制输入电压还是在系统动态调节过程中过多处于饱和状态,预设性能控制的高增益问题并没有解决,这将是下一步需要进行深入研究的内容.
3 自适应固定时间预设性能控制
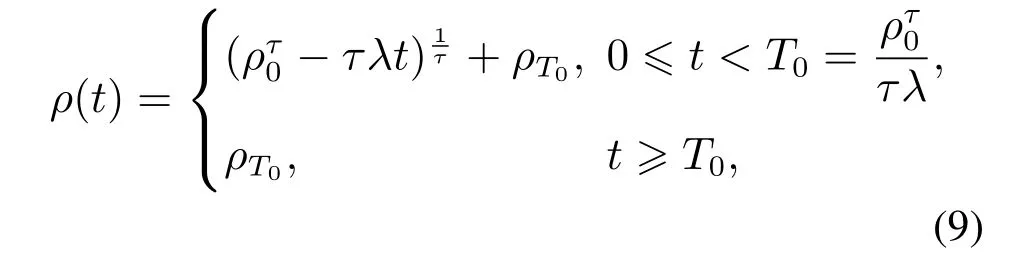









4 仿真验证


5 实验验证


6 总结

