基于递推规范变量残差和核主元分析的微小故障检测
秦玉峰,史贤俊
(海军航空大学岸防兵学院,山东烟台 264001)
1 引言
随着系统日益大型化和复杂化,故障诊断技术已成为保证系统安全运行的一种重要手段[1].按照故障引起的征兆大小,可分为显著故障和微小故障.微小故障在早期的主要特征是发展变化缓慢,故障征兆不明显,容易被噪声所淹没[2];随着时间累积,故障幅值缓慢增加进而发展成为显著故障[3],如果不及早发现,可能会导致系统失效从而引发严重后果.
微小故障的特点导致了在早期检测到微小故障的发生是非常困难的.现有的微小故障诊断方法主要包括基于知识的故障诊断方法、基于解析模型的故障诊断方法以及基于数据驱动的故障诊断方法.考虑到系统结构组成及功能的复杂性,基于知识和基于解析模型的故障诊断方法往往难以实施[4–5].因此,基于数据驱动的微小故障诊断方法成为了研究热点[6].其优点在于不需要完备的结构功能等先验知识,也不需要构建精确的物理模型.大量多元统计分析技术被用于微小故障检测领域[7–11].如:Harmouche等[12–13]针对传统主成分分析(principal component analysis,PCA)方法的T2统计量存在对微小故障不敏感的问题,提出了一种基于KL散度(Kullback-Leibler divergence,KLD)的微小故障检测方法;Zhang等[14]将PCA和KLD相结合,并对PCA所得到的投影向量进行优化,使得投影向量对于KLD故障检测方法是局部最优的;Chen等[15]基于KLD对非高斯电驱动系统的早期微小故障进行了检测,并分析了该方法在较宽信噪比范围内的鲁棒性能;Cai等[16]考虑到核主元分析模型不能敏感地检测微小故障初期的变化,引入KLD来度量核主成分的变化程度,提出了一种基于KLD–KPCA的微小故障诊断方法;陶松兵等[17]建立了基于协方差矩阵特征值变化与KLD变化的微小故障幅值估计模型;Gautam等[18]利用扩展卡尔曼滤波器建立故障检测指标和故障特征,然后基于KLD设计了故障决策统计量.与KLD类似,Zhang等[19]基于JS散度(Jensen-Shannon divergence,JSD)对早期微小故障进行检测和估计.上述文献利用概率密度函数对微小故障较为敏感的特点,通过衡量故障发生前后检测数据概率密度函数之间的差异,实现对微小故障的检测.这类方法通常需要假设检测数据服从正态分布,但是实际系统可能不满足该要求,因此应用范围受到一定限制.
另一类方法旨在提高残差对微小故障的灵敏度.如:Ruiz-C´arcel等[20]提出了基于规范变量分析(canonical variate analysis,CVA)的微小故障检测方法,并验证了该方法的故障检测效果优于传统的PCA方法;Wu等[21]将深度神经网络引入CVA中,利用贝叶斯推理分类器对故障进行分类;商亮亮等[22–23]在CVA中引入了一阶干扰理论,显著降低了计算负荷;此外,Pilario等[24–25]根据过去和未来规范变量之间的差异,构造规范变量残差,通过规范变量残差分析(canonical variate dissimilarity analysis,CVDA)来处理早期微小故障检测问题;Shang等[26]基于CVDA提出了一种加权平均统计量,提高了故障检测率;Li等[27]基于CVDA提出了一个新的故障检测统计量,对微小故障的发展变化更敏感,同时仍然保持低的虚警率,并改进了传统的贡献图方法,提高了故障可识别性;Chen和Luo[28]提出了一种新的多变量q-sigma规则来监测规范变量残差,并为每个变量都设置控制限,降低了检测延时和虚警率;肖姝君[29]将CVDA推广到非线性过程,提出了一种基于核规范变量残差分析(kernel canonical variate dissimilarity analysis,KCVDA)的故障检测方法;Pilario等[30]将不同的核函数进行组合,提出了一种基于混合KCVD的非线性动态过程早期微小故障方法.
虽然CVDA以及KCVDA在微小故障检测方面具有一定的有效性,但单一采用一种模型并不是最佳选择:CVDA仅提取数据中的线性特征,无法提取数据的非线性特征,这些非线性特征通常出现在线性模型的残差空间中[31];KCVDA将原始数据映射到高维空间,从而忽略了原有空间的信息.因此,若仅用线性或非线性模型进行故障检测,微小故障的可检测性是相对较低的.针对上述问题,本文提出了一种基于RCVD–KPCA的微小故障检测方法.其主要贡献在于:提出了一种混合统计建模方法,同时提取过程数据的线性和非线性特征,改进了非线性动态过程的早期微小故障检测性能,提高了微小故障的可检测性.
2 基于CVDA的规范变量残差构建
作为一种线性降维技术,CVA能够最大程度地关联过去和未来数据集[24–25].因此,可以根据过去数据集对未来数据集的预测程度检测出数据变化.CVDA在CVA的基础上,利用过去和未来规范变量之间的差异构造出规范变量残差,通过规范变量残差检测数据变化.下面介绍CVDA的具体实现方法.

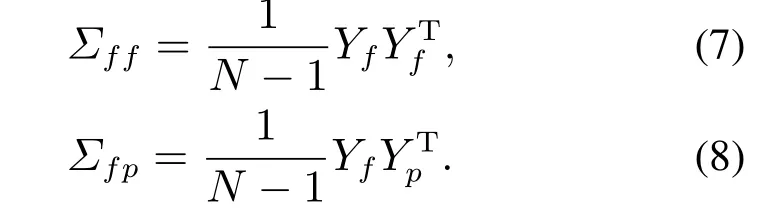
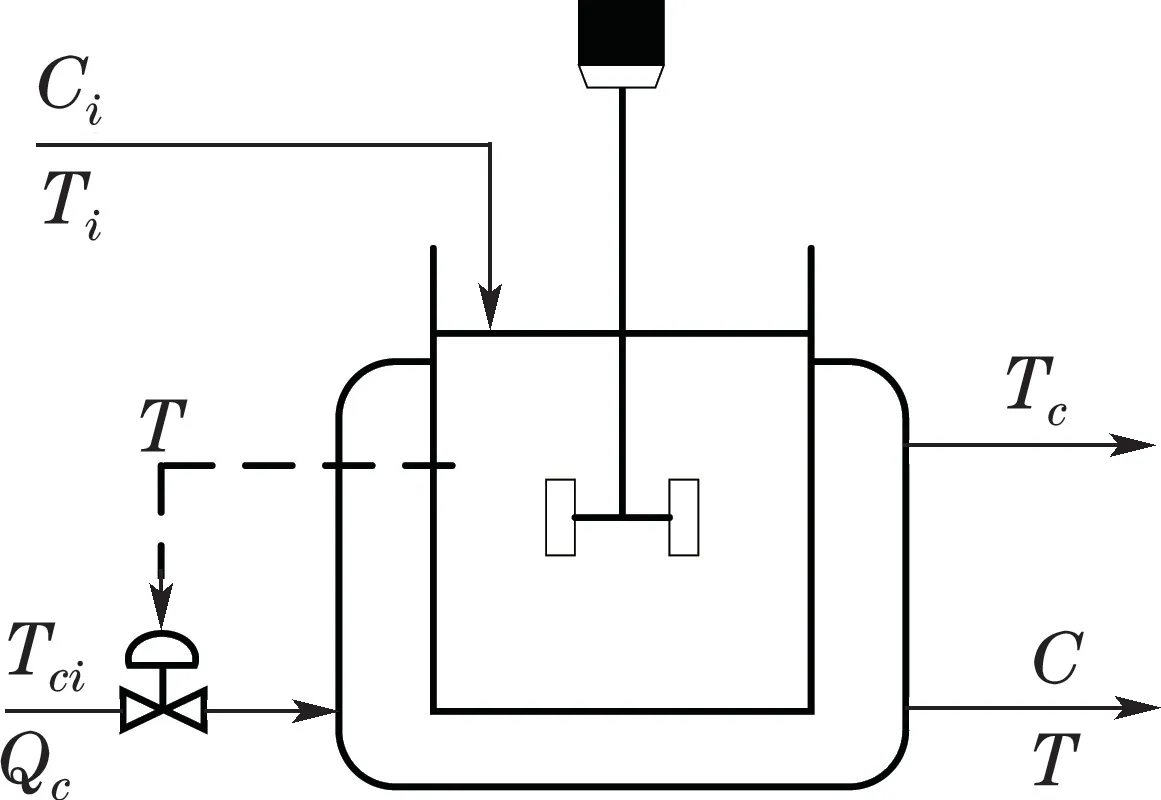
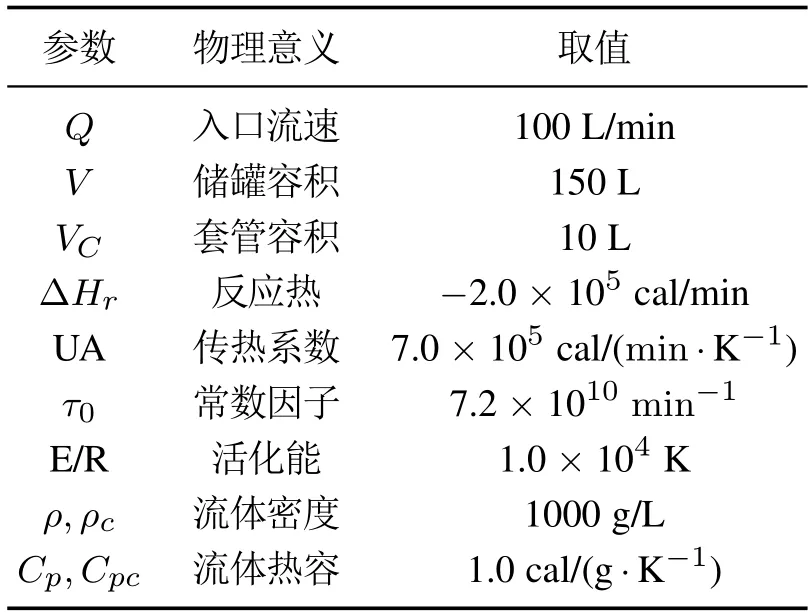
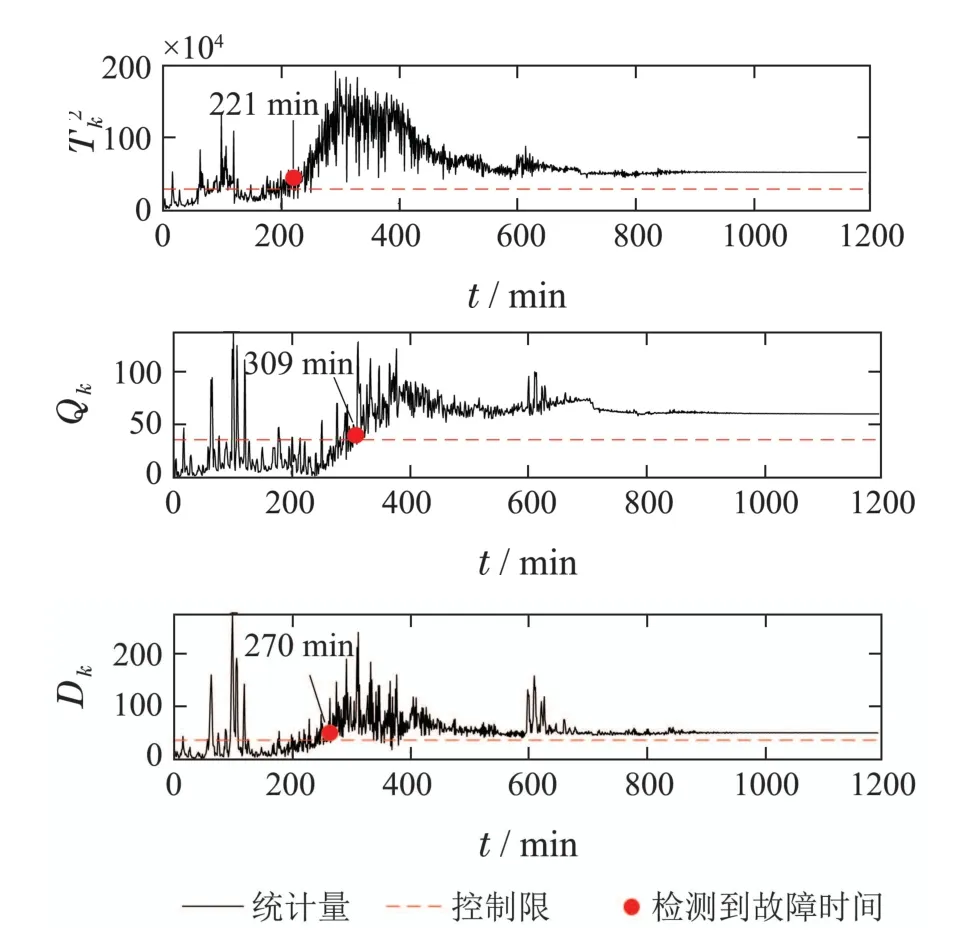
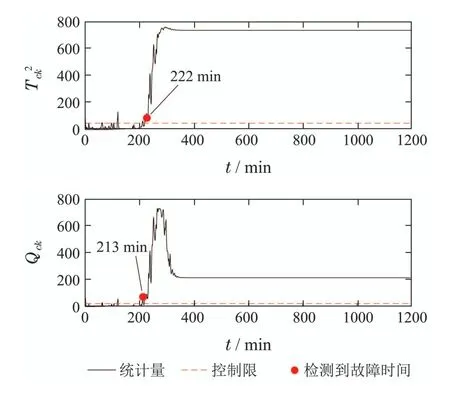
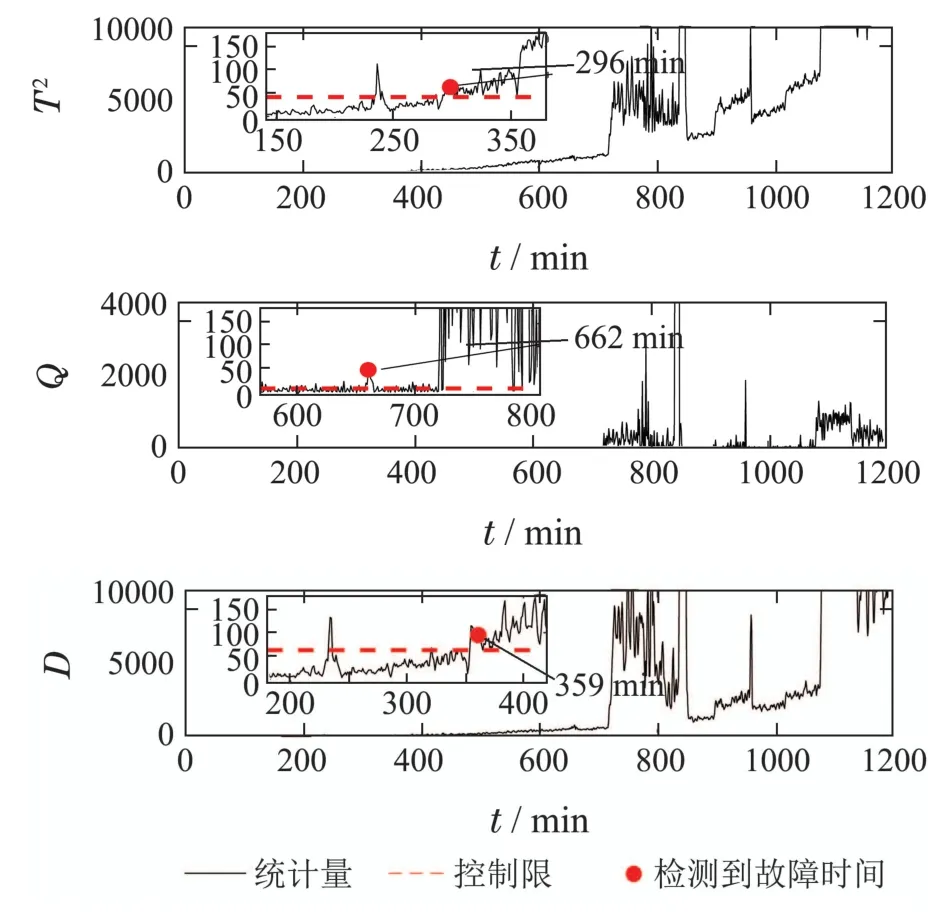
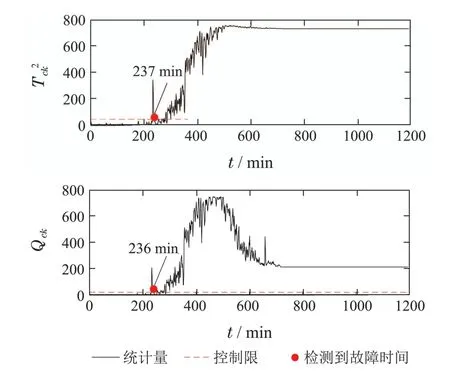
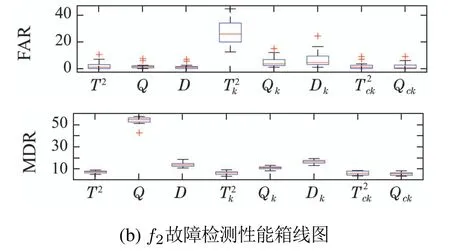
注1为了避免Σpp和Σff是奇异的,参数p和f需要满足:{mp,mf} CVA的目标是找到投影矩阵J和L,使得JYp(k)和LYf(k)之间的相关性最大化,其中JYp(k)和LYf(k)称为规范变量.投影矩阵J和L一般可以通过奇异值分解计算 式中:U和V分别是由左右奇异向量组成的矩阵.对角矩阵S由有序奇异值组成,S=diag{Σ1,···,Σγ,0,···,0},γ为矩阵H的秩.由于只有q(q 对于第k个检测样本,其状态向量x(k)和残差向量e(k)定义为 式中I为适维单位阵.利用x(k)和e(k)构造如下故障检测统计量: 其中:T2(k)统计量来度量状态向量x(k)的变化;Q(k)统计量度量残差向量e(k)的变化. 值得注意的是,过去观测向量对未来观测向量的可预测性可以有效地检测数据的微小变化[32].因此第k个检测样本的规范变量残差d(k)可以表示为 式中:Sq=diag{Σ1,···,Σq}.记所有样本的规范变量残差组成的矩阵为Yd,其协方差矩阵为 基于马氏距离的相关定义构造故障检测统计量D 文献[24]证明了统计量D(k)对微小故障检测的有效性,但它只能评估过程数据中线性特征的变化.由于线性模型的残差通常具有非线性特征,其影响不能与其他不确定性相分离[31],使得模型具有更高的控制限,从而降低了微小故障的可检测性.为了提高故障可检测性,有必要进一步提取规范变量残差d中的非线性特征.考虑到目前核方法技术成熟,因此本文应用KPCA方法实现非线性特征提取. 为了提高规范变量残差d对数据变化的敏感程度,首先采用指数加权滑动平均法(exponentially weighted moving average,EWMA)对d进行滤波处理.EWMA是工程系统过程测量中一种常用的数据处理方法[33],其求解过程实际上是一个递推过程.滤波后的数据可以用下式进行表示: 式中h为核宽度.因此,式(24)可以改写为 根据式(28)即可确定特征向量η1,···,ηN,及其对应的特征值λ1,···,λN.另外,在计算前需要对矩阵K进行均值中心化 核密度估计(kernel density estimation,KDE)是一种确定控制上限的常用方法[34],尤其适用于非线性或非高斯分布过程数据.考虑到实际检测数据不一定服从正态分布,本文利用KDE确定故障检测统计量的控制限. 假设x为一个随机变量,p(x)为x的概率密度函数.则 KDE中广泛使用的核函数是高斯核函数 通过高斯核函数估计x的概率密度函数 式中:ψ为带宽,x(i),i=1,2,···,N为x中第i个样本.设某一故障检测统计量为J,其控制限为JUCL.给定一个显著性水平α,则可以通过解决以下问题来计算JUCL: 若J≤JUCL,则认为没有发生故障发生;若J >JUCL,认为检测到故障. 总结本文所提方法,其总体流程图如图1所示.具体步骤如下. 图1 RCVD–KPCA算法流程图Fig.1 Flow chart of RCVD–KPCA algorithm 离线训练: 步骤1获取正常运行状态下的检测数据Y0,并对其进行标准化,得到标准化后的检测数据Y; 步骤2构造过去观测矩阵Yp和未来观测矩阵Yf; 步骤3分别计算Yp和Yf的协方差和互协方差矩阵; 步骤4对矩阵H执行奇异值分解,并确定主导奇异值个数q; 步骤5根据式(16)计算规范变量残差d; 步骤6根据式(19)对d进行EWMA滤波,得到滤波后的规范变量残差 步骤7构造核矩阵K并均值中心化,求解其特征值和特征向量; 步骤8根据式(30)–(31)计算主元得分向量; 使用闭环CSTR过程来验证本文所提出方法的有效性.该过程的数据由以下非线性状态空间模型模拟获得 其中:输入u=[Ci Ti Tci]T,Ci为反应物进料浓度,Ti和Tci分别为反应物进料温度和冷却剂进料温度.输出y=[C T Tc Qc]T,C为反应器中反应物浓度,T为反应器温度,Tc为冷却剂温度,Qc为冷却剂流速.ν1,ν2,ν3为过程噪声,噪声功率为10−4dB.τ为速率常数,满足τ=τ0e−E/RT,a与b的标准值为1,输出测量过程中存在均值为0,方差为0.05的高斯白噪声.CSTR过程的原理图如图2所示. 图2 CSTR过程原理图Fig.2 Schematic of the CSTR CSTR过程通过控制冷却剂流速Qc来维持反应器温度T,控制器设置为饱和度低于10 L/min和高于200 L/min.表1给出了方程中其他参数的物理意义及取值. 表1 CSTR过程参数物理意义及取值Table 1 Parameters meanings and values in CSTR 选取CSTR过程中的2个早期微小故障对本文所提方法进行验证,故障的具体形式如表2所示. 表2 CSTR过程中的微小故障Table 2 Incipient fault in CSTR 由系统状态空间模型(38)及原理图可知,当发生传感器漂移故障f1时,系统的过程参数不发生变化,仅输出信号中Tc的测量值发生改变,测量值随着系统运行逐渐增大;当发生冷却套管结垢故障f2时,b逐渐减小,直接对Tc,T产生影响,进而导致τ,C,Qc也发生变化. 仿真模拟运行时间为1200 min,所有变量的采样间隔为1 min,同时每隔60 min通过在输入u的标称值附近注入随机扰动w来改变操作状态,其中:w=[w1w2w3]T,w1∼N(0,0.002),w2,w3∼N(0,2).带有随机扰动的输入会导致系统动态发生变化,使得该过程非线性并且所得检测数据是非高斯分布的.在故障数据集中,正常运行200 min后引入故障.所有故障检测指标的控制限显著性水平α设定为0.99.选择p=f=3,φ=0.6,h=60.为了评价算法的故障检测性能,比较不同算法下故障检测延迟(detection delay,DD)、虚警率(false alarm rate,FAR)、漏检率(missed detection rate,MDR)等参考指标.由于故障类型为缓变的早期微小故障,因此故障检测统计量可能会在控制限的附近波动.为了明确检测到故障时间,本文定义检测到故障的时间为首次连续报警5次时的时间点.定义检测延迟为故障发生到检测到故障所经历的时间.虚警率和漏检率的计算方法如下: 式中:NFA为无故障发生时,J >JUCL的样本数;NNoFault为无故障发生的样本数;NMD为故障发生后,J 对于故障f1,其前200 min是正常数据,在第200 min引入了冷却剂温度传感器漂移故障.所得到的统计量监测图如图3–5所示. 图3 CVDA故障1统计量监测图Fig.3 Statistical monitoring diagram of f1 by CVDA 故障检测性能对比如表3所示. 表3 发生故障f1时的故障检测性能对比Table 3 Comparison of fault detection performance when f1 occurs 图4 KCVDA故障1统计量监测图Fig.4 Statistical monitoring diagram of f1 by KCVDA 图5 RCVD–KPCA故障1统计量监测图Fig.5 Statistical monitoring diagram of f1 by RCVD–KPCA 对于故障f2,其前200 min是正常数据,在第200 min采样点引入了冷却套管结垢故障.所得到的统计量监测图如图6–8所示.故障检测性能对比如表4所示. 表4 发生故障f2时的故障检测性能对比Table 4 Comparison of fault detection performance when f2 occurs 图6 CVDA故障2统计量监测图Fig.6 Statistical monitoring diagram of f2 by CVDA 在本案例中,故障检测统计量具有最低的故障检测延迟,但是其虚警率FAR明显高于其他统计量,因此在实践中是不可靠的.故障检测统计量和Qck的故障检测延迟与几乎相同,且和Qck的FAR和MDR分别为0%,7.3%和0%,5.9%,在所有的故障检测统计量中最低,说明和Qck的故障检测效果更好. 图7 KCVDA故障2统计量监测图Fig.7 Statistical monitoring diagram of f2 by KCVDA 为了检验本文所提方法的鲁棒性,为故障f1和f2分别生成15个测试数据集,每个测试数据集中过程噪声和测量噪声的强度与前文一致.所有测试数据集的前200 min都是正常运行数据,在第200 min注入故障.在得到所有的测试数据集后,测试CVDA,KCVDA,RCVD–KPCA的故障检测性能,结果如图9所示.图9(a)–(b)分别为故障f1和f2的故障检测性能箱线图,其中每一行箱线图分别对应DD,FAR和MDR结果.为了排除个别极端数据值的影响,选择15次故障检测结果的中位数表示故障检测性能的整体水平,如表5所示. 图8 RCVD–KPCA故障2统计量监测图Fig.8 Statistical monitoring diagram of f2 by RCVD–KPCA 图9 故障检测性能箱线图Fig.9 Fault detection performance boxplot 表5 故障检测性能箱线图中位数Table 5 Median of fault detection performance boxplot 在检测早期微小故障时,更早地检测到故障意味着延长了可用于处理故障的时间范围.在这一时间段内,可以根据故障的状态进行故障预测和基于状态的维护等活动.因此,及时检测到微小故障可以避免显著故障的发生.一般来说,一个好的故障检测指标必须具有较低的DD,FAR和MDR.综合15次实验结果来看,除了故障f1情况下的T2和D,Dk以外,相比T2,Q,D在DD和MDR方面有所提升,但是提升效果不明显,且鲁棒性较差,同时KCVDA引发的虚警数是最多的. 在两种故障场景下,本文所提方法得到的故障检测统计量与T2,Q,D相比,FAR具有相同水平,但是具有更小的DD和MDR;与相比,的3个指标都优于.与Q相比,Qck在检测时间上的改进幅度最大,也具有更好的鲁棒性.此外,和Qck在有效降低DD和MDR的情况下,虚警率没有显著提高,分别只有(f1:1.5%,f2:1.0%)和(f1:1.5%,f2:0.5%),因此是故障检测效果更好的统计量.由于CSTR过程同时包含线性和非线性关系,相比于传统的CVDA或KCVDA方法仅使用线性或非线性模型,RCVD–KPCA由于使用了线性–非线性混合模型,故障检测效果更好,上述实验结果验证了本文所提方法的有效性.综上所述,本文所提方法的优点如下:1)利用EWMA对规范变量残差进行滤波,提高了规范变量残差对数据变化的敏感程度;2)通过串联模型结构将CVDA和KPCA相结合,利用非线性主元对规范变量残差数据中的非线性变化进行准确捕捉,提高了故障检测效果. 本文提出了一种基于递推规范变量残差和核主元分析的微小故障检测方法.仿真结果表明,与传统的CVDA和KCVDA方法相比,本文方法所得到的故障检测统计量不仅能够更快地检测到微小故障,而且虚警率和漏检率较低,验证了本文方法具有较好的故障检测性能.进行故障检测的根本目的是为了诊断故障并给出解决方案,现有的基于规范变量残差的故障诊断方法绝大多数都是仅单独使用线性或非线性模型,这些方法无法用于本文所提出的线性–非线性混合模型,因此下一步工作将在此基础上进一步研究适用于本文所提模型的微小故障诊断方法.

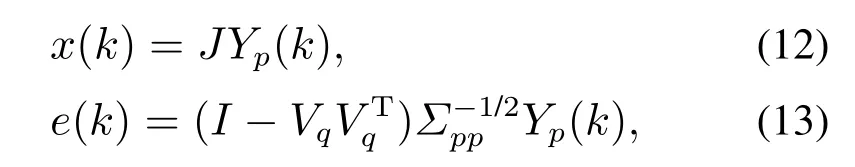

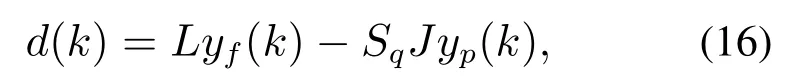
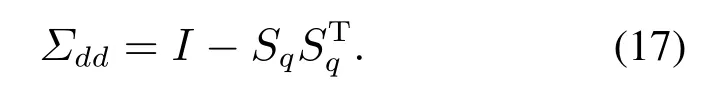

3 基于RCVD–KPCA的故障检测

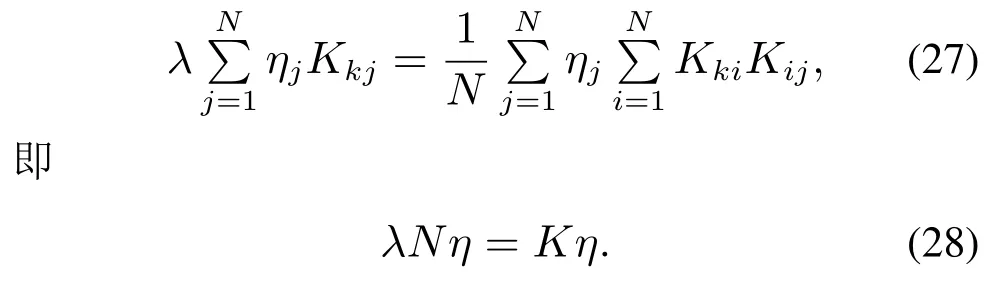

4 基于核密度估计的控制限设计
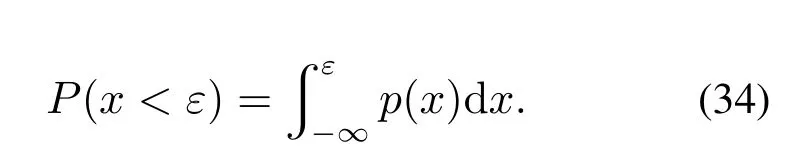





5 仿真分析











6 结论

