贪心选择在地铁站内行人疏散中的应用

邱杰凡 ,李志强 ,周小龙 ,徐瑞吉 ,单加响 ,方 凯

(1.浙江工业大学计算机科学与技术学院,浙江杭州 310023;2.中南林业科技大学生命科学与技术学院,湖南长沙 410004;3.衢州学院电气与信息工程学院,浙江衢州 324000)

1 引言

地铁站内通常具有面积大、空间布局复杂、人群高密度聚集等特点,在这些特点的背后往往存在着一些潜在的安全风险.例如,地铁站内出现突发情况,人们之间相互推搡的行为容易造成挤压、踩踏等群体性安全事故发生,给人们的生命和财产安全带来严重威胁[1].当前人群的应急疏导一般是以人工指挥为主,辅助以预先设置的疏散标志引导行人[2].有研究表明,群体系统协调与控制中“个体动态+通信拓扑”的结构特点可提升人群疏散效果[3].然而面对突发状况,由于难以预知行人的疏散轨迹,无法感知实时的疏散状态,有限的指挥人员和疏散标志难以持续有效的引导行人,会影响疏散的实施效果[4].因此,如何在疏散初始阶段制定合理的行人疏散方法极其重要.

当前人群快速疏散问题已得到国内外众多研究者的广泛关注,并取得了一定的理论研究成果[5–8].现有研究一般可分为人群疏散仿真研究、人群快速疏散方法研究两个方面[9–10].其中人群疏散仿真研究重点在于分析行人在真实疏散过程中的行为特点,构建行人行为仿真模型,对当前疏散场景设施布局或疏散方法提出优化建议或整改方案.然而,由于很难实时采集到行人的轨迹信息,此类仿真模型无法实时量化仿真算法与真实疏散环境的动态差异.在其上验证得到的动态疏散方法可能并不适用于真实疏散场景.

为此,本文提出了一种基于贪心选择的地铁站内行人疏散方法.首先,利用获取到的杭州武林广场地铁站的真实出站数据,基于元胞自动机构建行人轨迹半仿真模型,优化行人在出站闸机处的支付通过行为及移动速度表示,并利用真实出站数据反馈调节疏散仿真过程;其次,在半仿真平台中仿真疏散过程,基于个体状态信息,优化行人疏散时间评估方法,以满足高动态场景实时性要求为目标,采用复杂度较低的贪心选择策略分配最优疏散出口;最后,以武林广场地铁站为例,构建疏散仿真场景,利用真实出站数据设计对比实验,验证本文所提出的行人轨迹模型的有效性和出口分配方法的性能.实验结果表明,本文所提出的半仿真模型能够较好的模拟行人的轨迹,仿真中各出口疏散人数同真实出站数据拟合程度的可决系数R2达到了0.67.同时,本文所提出方法相较于最短路径和最短时间出口分配方法在整体疏散效率上分别提高27.2%和16.5%.

本文的主要贡献为:

1) 利用真实出站数据,构建基于元胞自动机的行人轨迹半仿真模型,并利用真实数据反馈调节仿真过程,弥补了传统仿真缺乏真实数据的缺陷.对比结果显示,半仿真模型中各出口疏散人数与真实出站数据拟合的可决系数达到了0.67;

2) 基于构建的半仿真模型,综合考虑疏散实时性以及算法复杂度,设计了基于贪心选择的行人疏散方法,该方法在兼顾实时性的要求下,保证了较高的疏散效率,能够应用于真实的疏散场景中;

3) 基于真实的地铁站以及行人出站数据,本文构建了高还原度的仿真场景,并通过真实数据设计对比实验,对半仿真模型以及不同算法的疏散效率进行了验证,实验结果表明本文提出的基于贪心选择的疏散方法与最短路径和最短时间出口分配方法相比,疏散效率分别提高了27.2%和16.5%.

本文在第2节中从人群疏散仿真和行人快速疏散算法两个方面介绍了当前国内外人群疏散领域的研究现状;第3节中介绍了基于元胞自动机的地铁站厅层行人轨迹模型;第4节介绍了基于贪心选择的行人疏散出口分配方法;第5节以某地铁站为例,通过仿真实验验证了本文所提出行人轨迹模型以及疏散出口分配方法的有效性.

2 国内外研究现状

当前人群疏散领域的相关研究,按照研究内容的不同可分为人群疏散仿真研究和人群快速疏散方法研究两个方面.

人群疏散仿真研究重点在于分析行人在真实疏散过程中的行为特点,构建行人行为仿真模型,模拟行人在特定场景下的疏散行为,针对仿真结果所发现的问题,对当前疏散场景设施布局或疏散方法提出优化建议或整改方案.Ji等人[11]针对一些特殊场景中人群密度较大问题,提出了一种三角网格元胞自动机模型,该模型为行人移动仿真提供了更多的可能性.Abdelghany等人[12]提出了一种基于仿真任务分配的两层模型框架,能够较为准确地再现特定区域的拥堵现象.Yang等人[13]研究了疏散引导标志类型以及标志所在位置对行人疏散过程的影响.Zheng等人[14]研究分析了多种因素对疏散过程的动态影响.Rozo等人[15]提出了一种在疏散路径拥挤时提供更优替代路径的疏散方法.Zang等人[16]通过模拟应急疏散过程中室内桌椅等障碍物摆放的密度和布局,揭示了二者对疏散效率的影响.Jiang等人[17]研究了人员检票失败时对不同布局、多检票点及多出口场景中疏散过程的影响.上述研究中提出的方法通过仿真模型层面的优化能够提升疏散模拟效果,但是依然无法从根本上解决仿真算法的缺陷,即无法实时量化仿真算法与真实疏散环境的动态差异.

人群快速疏散方法侧重于规划疏散路径,即通过采用特定策略进而控制人群疏散过程,为行人推荐安全、高效的疏散路径,或是提供相关信息指导人群进行疏散.江奎东等人[18]针对火灾烟气环境下的人员疏散问题,分析人员密度、可视条件等因素对疏散速度以及行人选择最佳疏散路径的影响,针对蚁群算法在求解最佳路径问题方面存在的局限性进行改进.刘杨等人[19]提出一种基于用户均衡理论的疏散人员出口分配方法,在复杂障碍物分布的多出口公共区域中,考虑不同疏散出口的宽度和远近情况,采用用户均衡分配策略分配疏散出口.Ruan等人[20]提出了一种动态元胞自动机模型,考虑了疏散过程中行人的记忆对疏散路径的影响.以上研究者提出的人群疏散方法更注重疏散路线规划而忽略了疏散整体时间,并且在考虑疏散人员分组时规划精细度不够,会造成部分疏散资源的浪费.

3 行人轨迹模型

3.1 地铁站布局和设施特点

地铁站在空间结构和设施布局上较为复杂,通常由站台层、站厅层、走行设施以及出入口等组成.其中站厅层是行人通往站台层和地铁站出口的中间区域,这一区域作为连接各个站台层和出口的通道,包含了车站服务台、收费闸机、安检等设施.地铁站内应急疏散过程中,行人通常会选择距离自己较近的出口作为逃生出口,导致出口处过度拥挤,通行效率低下.

3.2 人员行为特点及分析

通过对地铁站厅层行人移动过程的观察,发现在正常状态下和疏散状态下,行人在移动目的、移动速度、负重类型等方面均表现出一定的差异性,这些差异直接影响行人的疏散时间.应急疏散时,在可视范围内部分行人会根据出口距离、出口拥挤度、出口堵塞人数等因素评估疏散时间,从而选择最优疏散出口;疏散状态下,行人的移动速度将会更快,但是由于行人大多有不同程度的负重,所以在进行疏散时,行人速度变化幅度各不相同;此时,每个人都试图尽快完成疏散,出口处人群之间的摩擦系数增加,整体的疏散速度反而会降低;行人将会对障碍物或灾害有一定的趋避心理,在行为上主要表现为与其保持一定的距离或绕行等.

3.3 地铁站厅层行人轨迹模型

行人轨迹模型是疏散仿真的基础,将直接决定疏散仿真结果.在分析地铁站厅层设施布局及行人行为特点的基础上,本文提出了一种基于元胞自动机的地铁站厅层行人轨迹模型,该模型重新设计了行人在出站闸机处的支付通过行为及行人移动速度表示.

首先,本文通过地铁站工作人员获取了杭州市地铁1号线武林广场地铁站的出站数据,该数据包括列车到站时刻以及带有身份识别信息的行人通过出口处闸机的时刻.基于以上数据,可以估算行人从下车至出站过程消耗的时间.本文采用摩尔型元胞自动机构建行人轨迹模型.

将地铁站厅层空间划分为边长为0.5 m×0.5 m的网格空间,每一个网格表示一个元胞,所有元胞构成了系统的元胞空间.元胞所具有的状态分别为:空闲、被行人占据、被设施占据、被障碍物占据.因此,元胞状态集合可定义为

为了更准确地描述行人在正常状态和疏散状态下的行走细节,本文采用如下评估函数作为行人移动演化规则:

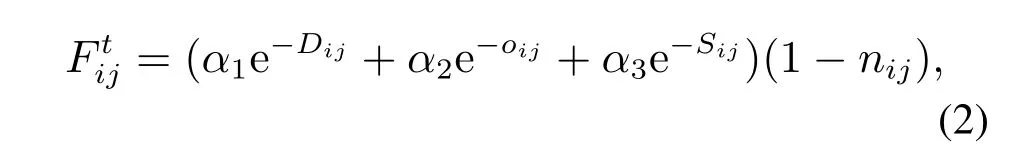
式(2)中:表示在t时刻,需移动元胞的邻点ij作为目标移动格点的评估分值;Dij表示在t时刻,邻点ij距离目标出口的距离;Oij表示邻点ij周围的障碍物占据格点数量;Sij表示邻点ij周围的灾害占据的格点数量;α1,α2,α3是对应各项权重系数;nij表示邻点ij是否为障碍物或灾难占据,如果被占据则nij取值为1,否则为0.

其次,需要构建出站闸机处的支付通过行为模型.正常状态下,行人首先行走至出站闸机处,需排队支付完成后通过闸机.这一过程可分为3个步骤:1)行人从起始点开始移动,行走至支付队列队尾;2)行人排队等待支付;3)完成支付并离开闸机通道.其中行人的支付时间和通过闸机通道时间均可通过统计数据获得,在仿真时可为行人分配范围随机数.

在疏散状态下,为能够以最快的速度疏散所有行人,地铁站工作人员可根据疏散要求打开闸机(不需要刷卡支付).地铁站工作人员在未打开闸机前,行人仍然需要刷卡通过.在闸机打开后,行人无需支付即可出站,此时可将闸机通道作为普通出口处理.闸机通道的疏散速度可结合Fruin模型[21]中人员流动系数经验公式间接计算

式(3)中:p表示出口演化时间内疏散人数;n表示出口处闸机数量;w表示闸机宽度;∆t表示演化时间;f表示人员流动系数.

最后,对行人移动速度表示模型进行设计.行人的移动速度对疏散过程起到了重大的影响作用.行人行走速度由其自身条件和周围环境双重因素决定.本文着重考虑了行人负重和周围行人密度对行人移动速度的影响.

在地铁站中,影响行人行走速度的自身因素主要是其自身负重,当行人随身携带大件行李时,其行走速度将会有明显的降低.张开冉等人[22]通过实验统计确定了负重时行人的行走速度,当行人携带小件行李和不携带行李时,对不同年龄阶段的行人的行动几乎不产生影响,但是当行人在背包、拎较大的手提包、携带行李箱时会对行人行走速度产生较大影响.行人负重时的行走速度Vl可表示为

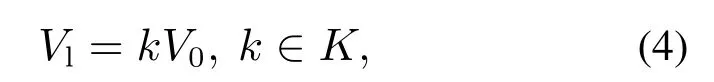
式(4)中:V0表示行人无负重或携带小件行李时行走速度;K表示不同负重类型对应的行人行走速度衰减集合.

另外,本文采用Fruin模型计算在一定人群密度下行人的行走速度Vf.行人的行走速度Vw可使用负重行走速度Vl和人群密度行走速度Vf表示为

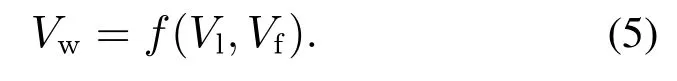
4 基于贪心选择的行人疏散出口分配方法

基于以上行人轨迹半仿真模型,本文可以通过行人的真实出站数据对参数进行优化,得到与真实情况接近的轨迹模型,并取得较好的仿真结果.为了保证在灾害发生时,行人能够第一时间得到最佳的疏散方案,在设计疏散出口分配方法时,必须重点考虑算法复杂度对疏散实时性和疏散效果的影响.为此,本文提出了一种基于贪心选择的行人疏散出口分配方法.

4.1 疏散时间分析

在使用疏散时间经验模型计算群体疏散时间时,如果将个人在设施或出口处排队通过时间定义为常量,在某些场景中并不适用.

如图1所示,A,B,C3个行人从同一个出口进行疏散,假设三者的疏散时刻分别为tA,tB,tC,行人C行走至出口处的时刻为wC.

图1 疏散次序Fig.1 Evacuation order

以Togawa经验公式为例,当计算行人C的疏散时间时,wC≤tB即行人C行走至出口处的时刻早于行人B的疏散时刻,但在行人C行走至疏散出口处这一段时间中行人A或早已以通过出口,此时若继续使用经验公式来计算行人C的疏散时间,将导致其疏散时间偏长;而当wC>tB时,即行人C行走至出口时刻晚于行人B疏散时刻,那么疏散时间经验公式将不适用于计算行人C的疏散时间.

4.2 疏散时间计算

为了能够更加准确估算行人的疏散时刻,本文针对地铁站厅层行人疏散提出了一种由行人个体移动速度决定的行走时间、行人在疏散出口处排队通过时间、出口处拥挤消耗时间共同决定的行人疏散时刻估算方法.

在疏散过程中,行人行走速度可表示为v,行人行走距离表示lm;疏散时行人行走至出口m的时间Tw可表示为

使用g表示当前出口处可用于疏散的闸机通道数;用f表示是否需要支付才能通过闸机,当需要支付时为1,否则为0;tp和tw分别表示支付时间和通过时间;w,r分别表示闸机通道宽度和行人流动系数.行人排队通过闸机的时间Te可表示为

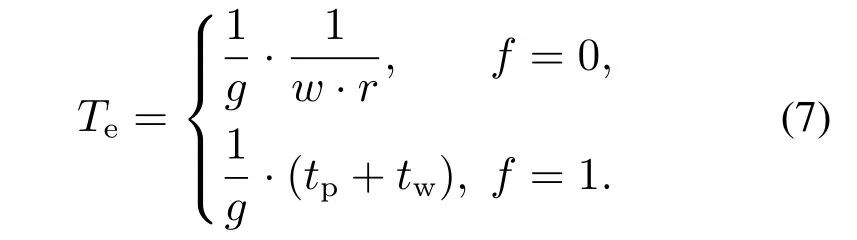
当出口处聚集大量行人时,越靠近出口处,行人密度越大.行人的移动速度受到周围行人的影响,随着周围行人密度增大而降低.行人周围行人密度为ρ时,受行人密度影响移动速度可表示v(ρ),那么当行人距离出口为R时,受拥挤影响行走至出口处时的移动时间可表示为

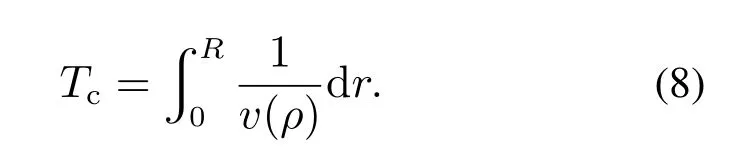
随着距离出口处距离r的增加,行人密度出现负指数衰减,可表示为ka−r,其中k表示行人的最大密度.在前方阻塞行人数p可知的情况下,阻塞区域半径R可通过求解式(9)得出

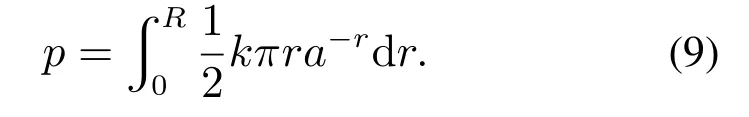
4.3 行人疏散时刻

行人i由出口m逃生的疏散时间由出口m完全疏散已分配人数时刻和行人i行走至出口m的时刻共同决定.将行人移动初始时刻记为T0,出口m完全疏散已分配人数时间记为Tm,行人行走至出口m处的时刻记为Tw,为简化论述过程,将行人排队通过时间与因拥挤造成的时间消耗之和用ts来进行表示.

分析Tm和Tw可知,当Tm≤Tw时,意味着行人到达出口m处时,出口m处仍有未疏散人员,行人i需要排队等待,此时行人i的疏散时刻可表示为Tm+ts.

综上行人疏散时刻可表示为

4.4 出口分配模型与贪心选择策略

本文针对疏散出口动态分配问题建立如下数学模型:

定义1疏散次序.疏散次序是指任意一种分配方式对应的所有疏散出口疏散队列中行人前后关系.

假设1行人疏散次序由行人到达出口的时刻所决定,即到达时刻越靠前,排序越靠前;

假设2每一种分配方式都对应唯一确定的疏散次序;

假设3开始疏散时,过往列车不再停靠,疏散总人数唯一确定;

假设4紧急疏散时,在出口处由于拥挤导致行走速度缓慢,会造成疏散时间消耗.并采用如下表1符号进行表示.

表1 模型符号表示Table 1 Model notation rules

将为n个行人分配疏散出口的所有分配方式的集合可表示为Qn,其中某一种分配方式可以表示为qn,在qn分配方式下疏散n个行人的完全疏散时刻可表示为,因此疏散n个行人的最快疏散时刻可表示为

第n+1个行人的最快疏散时刻可表示为

疏散n+1个行人时,最快疏散时刻

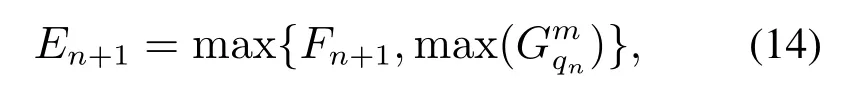
将n个行人分配到m个出口时,共有mn种分配方式,分配方式的数量将随疏散出口数量和待疏散行人数量呈指数级增长.使用暴力求解方法计算所有可能分配次序的疏散时间将耗费大量的计算时间,求解效率低.

为简化问题的计算过程,可以将n个行人的疏散出口分配问题划分为n次分配求解,每次分配根据当前的疏散状态为待疏散人群中的一个行人分配出口.由上一章节所建立模型可知,疏散n+1个行人的最快疏散时间En+1是由前n个行人分配次序所决定的疏散状态和第n+1个行人到达各出口的时间及其通过出口时间共同确定,因此只有第n+1个行人在疏散状态下,疏散时间最小即Fn+1取得最小值时,整体疏散时间最短.

因此,在保证疏散次序靠前的行人优先疏散的前提下,n个行人的出口分配问题可使用每次选取最小疏散时间的待分配行人并为其分配出口,即可对问题求解.根据问题特性和上述分析,基于贪心策略的行人疏散出口分配过程如下:

1) 第1次分配时,计算所有待疏散行人行走至各疏散出口的时间,并对行走时间排序;

2) 将最小行走时间行人作为分配对象,最小行走时间所对应出口为其最佳疏散出口,并计算疏散时间;

3) 将行人加入到其疏散出口对应的疏散行人队列,在待分配行人中去除该行人;

4) 计算所有待疏行人疏散时间;

5) 将最小疏散时间行人作为分配对象,最小疏散时间所对应出口为其最佳疏散出口;

6) 将本次为其分配出口的行人加入到其疏散出口对应的疏散行人队列,在待分配行人中去除该行人;

7) 重复4)–6),直到为所有行人都分配出口.

5 实验结果与分析

5.1 行人轨迹模型

如图2(a)所示,以杭州市武林广场地铁站的站厅层作为疏散场景原型,站厅内付费区域呈长方形;付费区域的周围有6个闸机簇,每个闸机簇闸机数量不等;付费区域内按照一定的设计要求分布着框架柱;付费区域中分布着扶梯与直梯,供行人下降到站台层或上升到站厅层.根据站厅层公共设施和建筑布局,本文构建了如图2(b)所示疏散场景,其中行人占据的空间被近似为具有刚性的圆形.

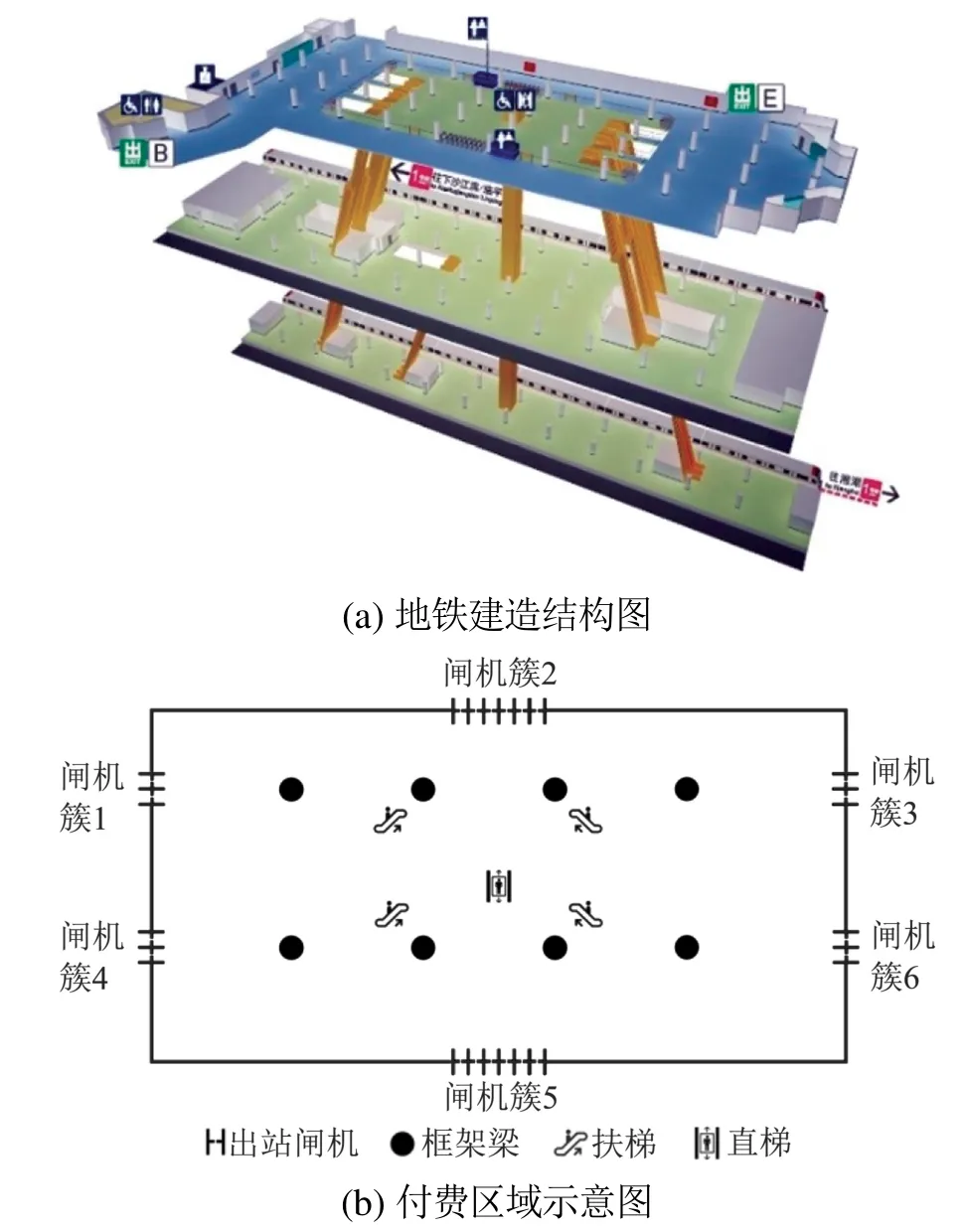
图2 疏散仿真场景Fig.2 Simulation of evacuation scenarios

仿真参数主要包括疏散场景基本参数、行人基本参数,如表2所示.行人基本参数及取值如表3所示,速度单位为m/s.

表2 疏散场景参数取值Table 2 Parameter value of evacuation scene

表3 行人参数取值Table 3 Parameter value of pedestrian

如图3(a)所示,仿真实验开始时,行人随机分布在疏散场景中.在正常情况下,行人将根据自身的出行目的选择目标出口,随后行走至出站闸机,支付完成后由闸机通道出站.当行人到达速度大于行人出站速度时,将会在闸机处形成如图3(b)所示阻塞人群,行人排队等待支付出站.

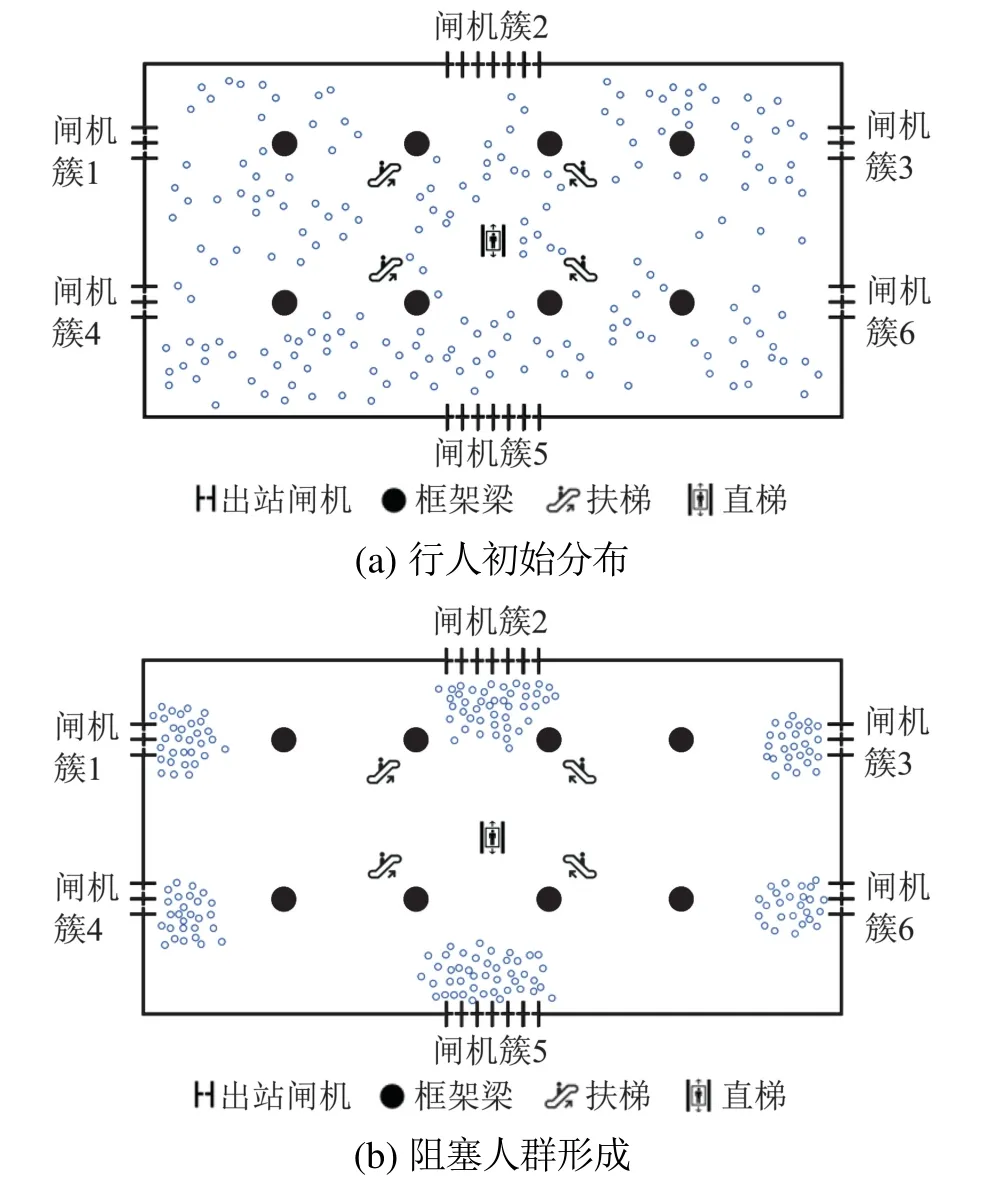
图3 疏散仿真过程Fig.3 Simulation of the evacuation process

分析地铁站工作人员提供的行人出站刷卡记录,该地铁站高峰时期某小时出站行人为1064人,现将实际行人刷卡时间点作为仿真实验中行人开始行走时间点,模拟行人出站过程.图4(a)为仿真过程中每分钟出站行人数与实际出站行人数折线图.由图4(a)可以看出,两条折线高度拟合.经计算,用以度量拟合程度的可决系数R2为0.67,说明本模型能够较好的模拟真实的行人出站行为.

根据实际行人出站刷卡记录,该站行人出站最高速率为3.64人/s.为进一步验证本文提出的轨迹模型的有效性,进行如下实验:模拟出口闸机满负载情况,对比30 s时间内仿真实验出站行人数与实际出站行人数.实验结果如图4(b)所示,仿真模型模拟的闸机通过人数与真实闸机通过人数基本一致,这也进一步证明了本仿真模型对不同速率的行人轨迹估计的有效性.

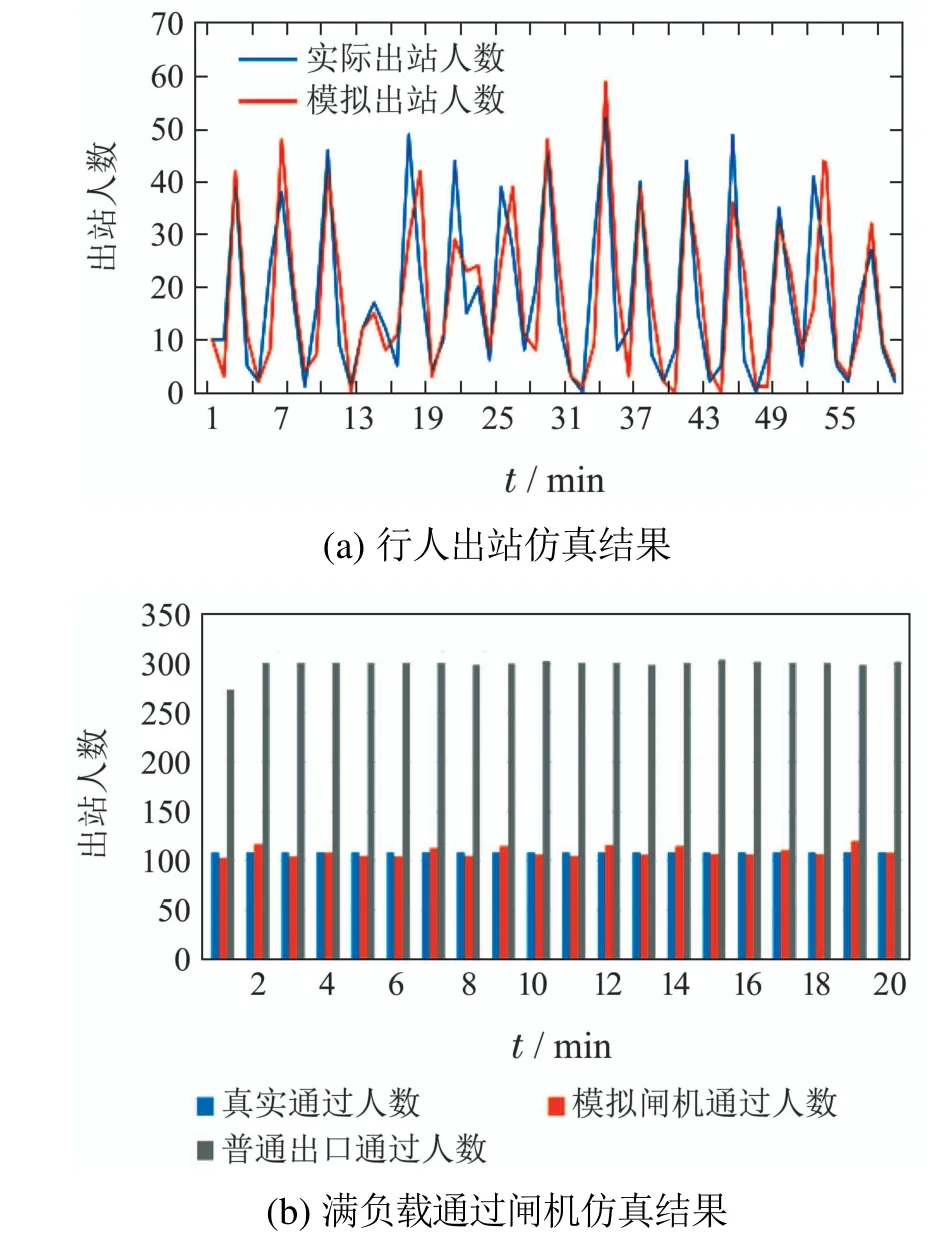
图4 出站仿真实验结果Fig.4 Simulation and experimental results of evacuation

5.2 出口分配方法

为了验证本文所提疏散出口分配方法的有效性,现对最短路径出口分配方法、最短时间出口分配方法以及本文所提出的基于贪心选择的行人疏散出口分配方法进行实验,并分别对疏散过程中使用各方法时各疏散出口疏散人数和整体疏散时间两个角度进行分析.

其中:最短路径分配方法即计算行人到达所有疏散出口处的距离,选取距离行人最短的出口作为最优出口.该方法相对其他方法具有计算过程简单、计算量小,能够快速的为大量的用户分配疏散出口等优势;适用于一些行人个体运动能力相似、距离各个出口相近的疏散场景.但是该方法仅考虑行人到各出口的距离,未考虑行人移动速度和疏散通道状况等其他疏散影响因素.在大多数的疏散场景下,部分疏散出口不能够得到有效利用,整体疏散时间仍可以被进一步缩减.最短时间的出口分配方法则根据行人从各出口疏散时间的长短来确定行人的最优疏散出口.时间的计算通常是利用疏散时间经验模型计算.经验公式通常会考虑出口宽度、疏散通道长度等参数对疏散时间影响.一般情况下,如果疏散时间估算准确,最短时间的出口分配方法能够较为准确的将行人分配到各个疏散出口.但是在几乎所有真实场景中,疏散时间估算并不准确.极端情况下,个别出口在其他出口早已疏散完成时仍未疏散所分配行人.

根据武林广场地铁站特定时间点的真实出站数据,本文设定实验初始时在地铁站厅层随机分布260人,实验开始后行人由站台层通过楼梯或电梯到达站厅层,所有站台层行人全部上升到站厅层用时60 s,行人总数在这一过程中持续增加,在60 s后,站厅层所有行人都到达站厅层时,模拟行人总数为1115人.

图5(a)为使用最短路径方法为行人分配疏散出口时,各疏散出口疏散人数随时间变化的折线图.从图中可知由于原始状态下站厅层有随机分布的行人,各出口均有行人疏散,30 s以后,其他出口(闸机簇1,3,4,6)疏散人数不再增加,仅有距离最近的出口2(闸机簇2)和5(闸机簇5)在不断承担疏散任务,在整个疏散过程中距离较远的疏散出口并未被利用,从而导致疏散资源的浪费.

图5(b)为使用最短时间方法为行人分配疏散出口时,各疏散出口疏散人数随时间变化的折线图.由于出口2和出口5闸机数量为其余出口闸机数量的3倍,因此出口2和出口5疏散人数应为其余疏散出口的3倍,从图中可知出口2和出口5并未被充分利用.

图5(c)为使用贪心策略为行人分配疏散出口时,各疏散出口疏散人数随时间变化的折线图.从图中可知,闸机2和闸机5疏散人数约是其他4个出口的3倍,与闸机数量比一致,表明各出口都能够以较高的效率疏散行人.

如图5(d)所示,疏散状态下,使用3种方法进行疏散出口分配时整体疏散时间分别为125 s,109 s,91 s,使用贪心选择策略为行人分配疏散出口时,相对其他两种方法分别节省了34 s与18 s,疏散效率相对提高约27.2%,16.5%.

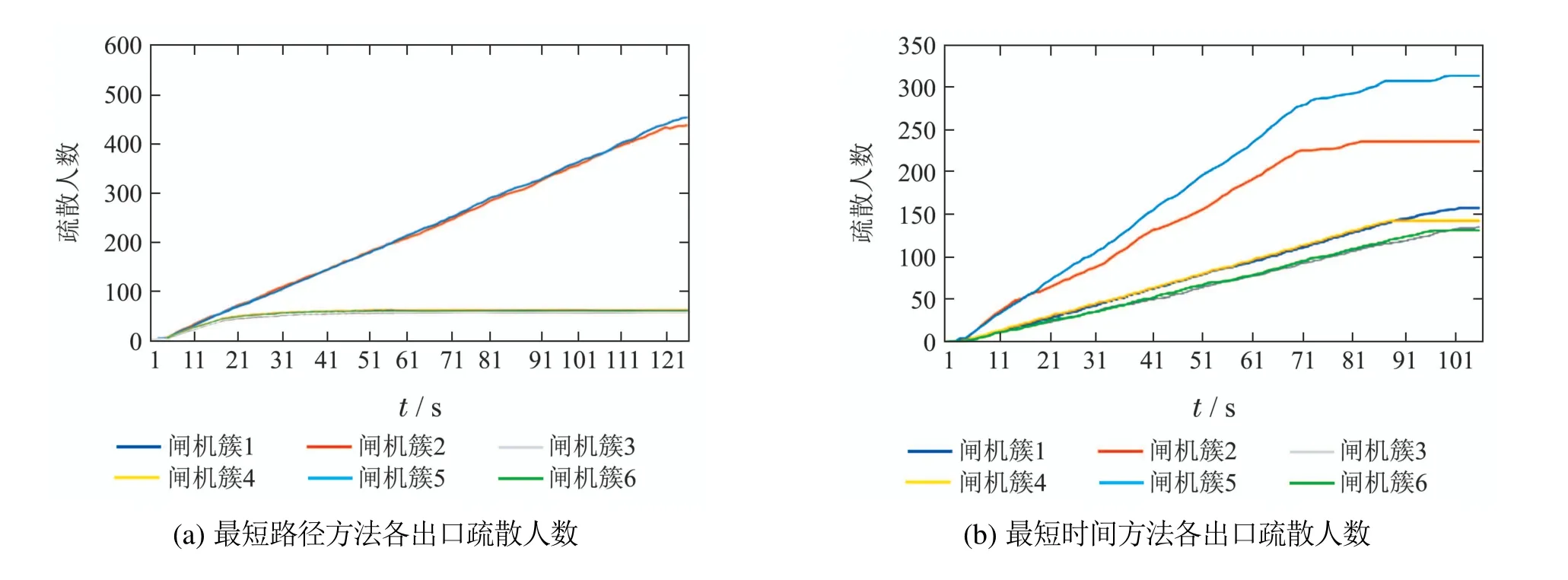
图5 各出口疏散人数变化及总人数变化Fig.5 The number of evacuation and the total number variation

6 总结与展望

为了提高行人疏散效率,本文从行人疏散出口分配角度出发,提出了一种基于贪心选择的地铁站内行人疏散方法,目的在于解决当前行人疏散出口分配方法存在的疏散出口利用不均、应对突发情况能力较弱等问题.真实环境中疏散状态信息的获取难以保证,且信息采集设备种类多、数量大、成本高.本文提出了半仿真模型设计,即通过实际数据不断优化半仿真模型,有效解决了在实际生活中大量群体性数据无法获取的问题,具有一定的创新性.进而,利用这种半仿真模型,本文也验证了贪心选择策略应用于行人疏散的有效性,从而提高了疏散的实时性.

本文采用真实数据构建半仿真模型,尽管能够实现对普通场景下大多数行人的出站模拟,但仍缺少紧急疏散场景下的有效数据.在未来的工作中,本文将进一步有针对性地利用多种定位手段,采集紧急疏散场景下行人的行动轨迹,进一步利用真实疏散轨迹数据不断优化疏散仿真模型.