MOb–GRU神经网络工业软测量建模方法与输出预测

王 珠,刘佳璇

(中国石油大学(北京) 自动化系,北京 102249)

1 引言

随着自动化水平的提升、质量要求的完善、生产规模的扩大,现代工业过程往往存在强非线性、动态特性与慢时变等本质特点,众多参变量中普遍存在不确定、多层次与强耦合关系,因此传统的机理模型难以准确地描述实际工业过程.

软测量技术[1]的产生与发展为解决上述问题提供了一种有效方法,其核心思想是利用易于测量的过程变量(辅助变量)建立可以表征过程变量和质量变量(主导变量)之间关系的软测量模型.软测量模型为后续过程控制[2–3]、在线估计[4–6]以及故障诊断[7]等方面产生了很大的影响,发挥了必要且重要的作用.早期的软测量是基于机理分析的建模,需要对工业过程内部机理有充分的了解.其中:微分方程与代数方程能够用于表示工业过程动态机理[8],卡尔曼滤波[9–10]常用于软测量中对过程参数进行建模.但由于实际工业过程极为复杂,模型结构的形式难以确定,很难通过机理建模描述过程规律、反映过程特性.基于数据驱动[11]的软测量建模方法解决了上述问题.数据驱动仅依靠现场采集的大量历史输入输出数据建立质量变量与过程变量之间的数学关系,因此非常适合于复杂工业过程的软测量建模.早期的数据驱动建模方法包含主成分分析法(principal component analysis,PCA[12])、偏最小二乘法(partial least squares,PLS[13])等回归分析法与人工神经网络(artificial neural network,ANN)等机器学习模型[14].由于实际工业过程具有动态特性,但上述回归分析法与多数人工神经网络模型仅能反映过程的非线性特性而缺少对动态特性的体现,因此非线性动态建模成为软测量的主要研究方向,不少研究针对时序数据具备的特性提出了非线性动态软测量模型[15–17].

近年来,随着神经网络理论的不断发展和完善,神经网络软测量模型主要包含普通神经网络[18]、径向基神经网络(radial basis function network,RBF[19])、生成对抗神经网络(generative adversarial network,GAN[20])等模型.但上述提出的模型都是静态软测量模型,在工业过程中具有一定的局限性.动态软测量模型的相继提出解决了静态模型在实际应用中估计精度低、鲁棒性差等问题.回声状态网络(echo state network,ESN[21])、卷积神经网络(convolutional neural network,CNN[22])与循环神经网络(recurrent neural network,RNN[23–25])等常作为动态软测量模型应用到实际的工业过程.其中:循环神经网络的发展为时间序列的建模提供了优良选择.因此,对于工业过程的非线性全动态建模问题,常使用工业时序数据作为循环神经网络的输入或采用固定结构的记忆神经网络对非线性动态过程进行有效模拟.记忆神经网络分为循环神经网络、长短期记忆神经网络(long-short term memory,LSTM[26])和门控循环单元(gated recurrent unit,GRU[27]).其中:循环神经网络是一种短记忆模型,不适合处理过长的时间序列;LSTM的提出解决了上述问题,在记忆方面得以较大提升,对任意长度的时序数据均能进行很好的训练及预测,但该网络的结构过于复杂,加重了计算负担.为解决上述问题,GRU的提出得到了广泛的应用.Fu等[28]使用GRU神经网络对交通流进行了预测,实验表明,GRU在交通流量预测上的性能优于LSTM与自回归积分移动平均(autoregressive integrated moving average,ARIMA)模型.Pavithra等[29]将门控循环单元应用于医学领域,基于GRU在预测糖尿病疾病的发展上取得了良好的预测效果.Siwagorn等[30]采用GRU 预测飞机垂直速度的下降幅度,使飞机能够有效着陆,提高了飞机的着陆效率.倪维成[31]建立了一种基于GRU的航空发动机剩余寿命预测模型,实验表明该模型在预测精度上高于多数浅层机器学习方法和部分深度学习方法.虽然目前已有大量学者在不同领域验证了GRU神经网络较其他预测模型在时序预测问题上的优越性,但基于GRU对工业领域中非线性动态过程的预测研究却屈指可数,并且已有研究没有对GRU神经网络反向更新单元数与实际非线性动态过程阶次之间的关系进行研究.基于以上分析,本文提出一种依赖模型阶次的GRU(model order based–GRU,MOb–GRU)软测量模型,基于该模型对工业领域中单变量与多变量非线性动态过程进行全动态建模,本文用带有输出非线性的非线性动态过程代替实际非线性动态过程产生过程数据,进而进行分析与建模.

Lynn等人[32]的研究表明,GRU结构的更新门和输出激活函数是GRU网络最关键的组件,学习率是门控循环单元最重要的超参数.因此,建立神经网络软测量模型的关键是选择合适的学习率优化算法使网络以较快速度达到收敛.目前已有一些关于深度学习模型中学习率策略的研究.Ranjeeth等[33]提出了具有最优随机梯度下降(stochastic gradient descent,SGD)的多层感知器机器学习模型,SGD的引入提高了感知器的性能与数据分类准确度,但SGD中学习率是固定的,收敛速度慢且容易陷入局部最优解.Ralf等[34]设计了一种应用于复杂深度强化学习(deep reinforcement learning,DRL)问题的循环学习率方法,该方法较固定学习率方法能达到更好的结果,但循环学习率是在两个有理边界值的范围内变化,而不是单调衰减的.为解决上述问题,本文设计了一种简单而有效的阶跃衰减类(step attenuation class,SAC)自适应学习率算法与学习率矩阵算法,两种方法均保证了整个系统更快地收敛和稳定,提高了预测的准确率.

2 针对非线性动态过程的MOb–GRU网络结构与信息流向图

GRU由Cho等人提出,是LSTM的一种变体模型,不仅能够解决RNN存在的梯度消失问题,还简化了LSTM的网络结构、提高了收敛速度.目前最常用的GRU模型主要由更新门和重置门构成,图1为其内部结构示意图.

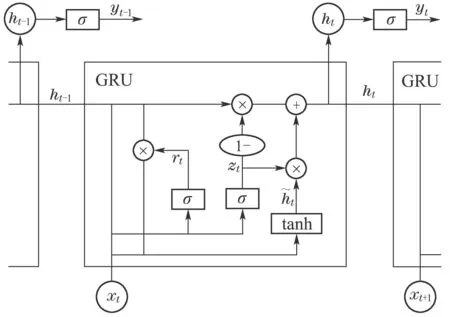
图1 GRU内部结构示意图Fig.1 GRU internal structure diagram

每个GRU单元能够根据当前时刻的输入xt和上一时刻隐藏层输出的激活值ht−1,计算得到当前时刻隐藏层输出值ht和候选激活值˜ht.相比于RNN,GRU通过引入门控机制,能够同时对不同时刻、不同长度的时序关系进行记忆和学习.相比于LSTM,GRU减少了网络参数数量,加快了训练的收敛速度,具有简单的单元结构和高效处理数据的能力.目前GRU已被广泛应用于机器翻译和序列生成等众多领域.

本文所提出的MOb–GRU软测量模型适用的场合需满足以下两个条件:1)由于工业过程的复杂性,过程内部机理不清楚,无法运用机理建模对其进行精确建模;2)过程数据在时间上连续,满足一定的时序关系.文中分别采用ut和yt来表示过程变量和质量变量,软测量模型基于数据驱动,通过学习得到过程变量与质量变量间的映射关系,即f:yt →ut.

MOb–GRU神经网络与传统GRU相比,网络结构复杂度与训练所需计算量均较小,原因在于:a)从结构上看,MOb–GRU能够根据实际过程的大致阶次调节反向更新单元数,其数量可少于网络中的总单元数,与传统GRU从第1个模块开始输出相比,既保证了长期和短期的记忆性,又在结构设置上变得更加灵活.需要注意的是,MOb–GRU的反向更新单元数是指包含最后一个模块开始反向向前传播的单元数,与训练算法中权重梯度在时间上的叠加数量相等,以此保证了权重在更新过程中不随噪声发生显著波动;b)从训练算法上看,在用随时间反向传播(back propagation through time,BPTT)算法进行训练时,MOb–GRU综合梯度量的确定依赖于反向更新单元数,而GRU综合梯度量的确定依赖于全部模块数.基于此,MOb–GRU训练时历经时间确定梯度所需的循环数量较小,计算量较低,减轻了模型的计算负荷.但MOb–GRU神经网络与RNN相比,网络结构复杂度与训练所需计算量又是偏大的,原因在于:a)从结构上看,RNN中间层神经元的状态是由上一层过程输入的状态与自身前一时刻的状态决定的,意味着与GRU,MOb–GRU相比,RNN总模块数只有2个;b)从训练算法上看,RNN综合梯度量的确定只需计算当前和前一时刻的梯度量,即反向传播单元数为1,因此训练所需的计算量相对更低.综上所述,RNN与GRU,MOb–GRU相比,网络结构更简单,训练时的计算时间复杂度更低.3个模型的计算时间复杂度关系如表1所示.

表1 3个模型的计算时间复杂度Table 1 Computational time complexity of three models

基于对模型计算时间复杂度与训练性能的考虑,本文采用MOb–GRU模型对非线性动态过程进行建模,将过程的输入数据ut和输出数据yt作为神经网络的学习数据,无需明确过程内部机理和参数变量.本文设计的单变量MOb–GRU(SISO–MOb–GRU)信息流向图和单变量GRU(SISO–GRU)信息流向图如图2所示.其中:j为前向传播单元数;i为反向更新单元数;以SISO–MOb–GRU信息流向图为例,每个单元下方直连的变量为MOb–GRU单元的输入变量,上方直连的变量为MOb–GRU单元的预测输出.定义x(t)=[u(t −1)y(t −1)]T为MOb–GRU单元的输入;χ(t)=[x(t −j)··· x(t −i)··· x(t −1)],(t)=[(t−i+1)···(t)]分别为网络的输入和输出.为体现过程的动态特性,本文将采用递归的方式给网络的输入信号赋值,使MOb–GRU模型呈现出一种动态效果.SISO–GRU信息流向图中的变量同理.

图2 单变量MOb–GRU与单变量GRU信息流向图Fig.2 SISO–MOb–GRU&SISO–GRU information flow diagram

高维、高阶多变量过程普遍存在于现代工业过程中,因此基于MOb–GRU对多变量过程进行动态建模具有重要的实际意义.由于本研究限于理论分析层面,在单变量过程建模的基础上仅通过拓展维度便能实现对多变量过程的模拟及预测.图3为本文设计的多变量MOb–GRU(MIMO–MOb–GRU)信息流向图.其中:s和v表示多变量非线性动态过程输入与输出变量的维度.每个MOb–GRU单元的输入变量引出的小圆圈数量代表网络的输入维度.对于多变量过程,每增加一个输入或输出变量,便会多一个黄色圆圈与网络的输入变量相连,以表示网络输入维度的拓展;输出维度的拓展同理.多变量GRU(MIMO–GRU)信息流向图与MIMO–MOb–GRU信息流向图的区别和单变量一样,在此不呈现具体的MIMO–GRU信息流向图.

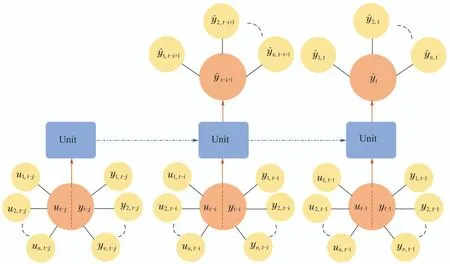
图3 MIMO–MOb–GRU信息流向图Fig.3 MIMO–MOb–GRU information flow diagram

3 方法

3.1 算法流程与训练算法

基于MOb–GRU神经网络对非线性动态过程进行建模与预测的整体算法流程如下:

步骤1输入输出数据的归一化处理.本研究将根据过程变量与质量变量的量程范围进行归一化和反归一化处理.

其中:ut,max和ut,min为输入变量量程范围内的最大值与最小值;yt,max和yt,min为输出变量量程范围内的最大值与最小值.

步骤2初始化网络结构选择.

步骤3训练网络.本研究将采用BPTT对MOb–GRU网络进行训练.

步骤4步长及步长矩阵的选取.本文采用SAC自适应学习率算法与学习率矩阵算法选取合适的步长与步长矩阵对网络参数进行更新,以确定最优的网络结构.

步骤5预测输出.

BPTT算法是记忆神经网络训练时进行权重更新的一种基于时间的反向传播算法,其本质为梯度下降法,因此求各参数的梯度成了该算法的关键.首先定义t时刻的损失函数为

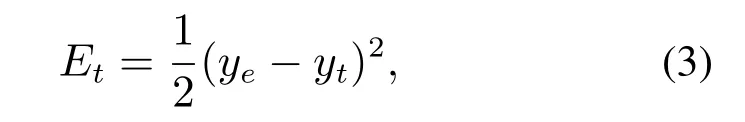
其中:ye表示t时刻的实际输出;yt表示t时刻的预测输出.BPTT训练算法具体见文献[35].

3.2 学习率优化算法

学习率对神经网络的学习有很大的影响.学习率过高,易使网络参数优化过度,导致训练变得发散;学习率过小,虽然网络训练更加可靠,但所需时间过长.因此选择合适的学习率优化算法显得尤为重要.

3.2.1 阶跃衰减类SAC自适应学习率算法

对于不同波动程度的非线性动态过程会对应不同的最优学习率(optimal learning rate,Olr),以保证网络的预测精度和收敛速度.因此本文设计了1种SAC自适应学习率算法.

引入平均绝对百分比误差(mean absolute percentage error,MAPE)作为评价指标,用于判断模型训练效果的好坏,即

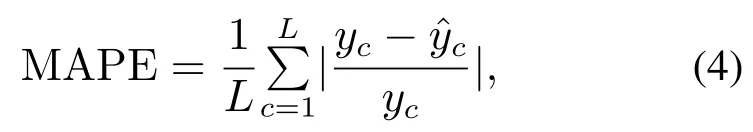
其中:L为训练数据的长度;yc为c时刻的真实输出;为c时刻的估计输出.

将训练数据按时间连续划分为n个长度为l的阶段,将预选学习率中的固定学习率从大到小依次分配给[2,n −1]的每个阶段.第1阶段采用初始学习率作为网络的Olr进行训练;第2阶段到最后一个阶段之间的每一阶段,首先确保网络在该固定学习率下收敛,接着取后0.25l的数据通过递推式(5)计算MAPE数值,并将该值作为本阶段的相对误差标准值,即

其中:dl−0.75∗l=(1−b)/(1−bl−0.75∗l),b表示遗忘因子;q ∈[2,n −1],表示某一阶段.最后记录每一阶段最后一个时刻的MAPE和学习率.

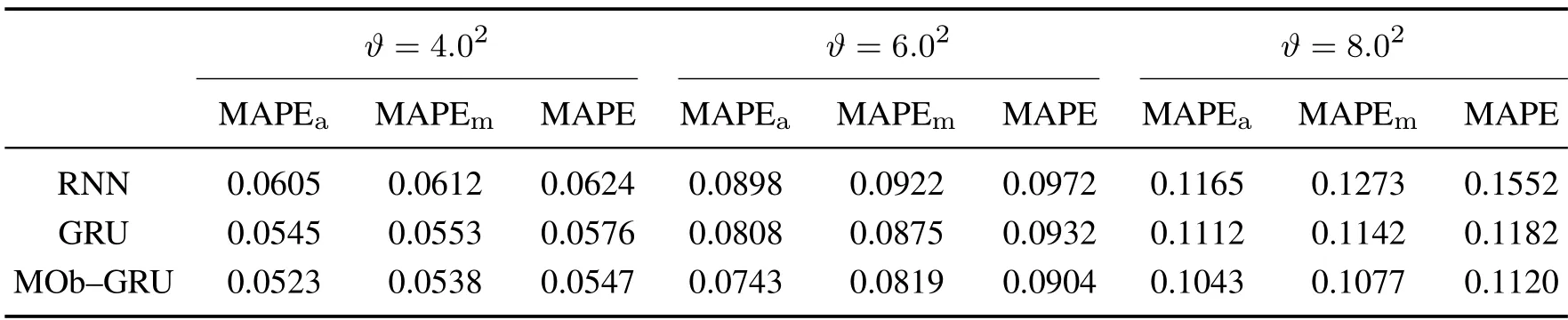
在判断阶段,将当前阶段的MAPEq与最优MAPE进行比较,若MAPEq

通过不断调整最优MAPE确定最优学习率的取值,具体实现流程如下:

步骤1判断当前时刻c处于哪个阶段.

步骤2如果q=1,则设置初始学习率为最优学习率,用于神经网络的稳定和收敛.如果q=2,则在该阶段的最后通过递推公式计算初始MAPE作为相对误差标准值.

步骤3如果2

步骤4如果q=n,使用最优学习率训练神经网络并进行最优网络结构的确定.

利用SAC自适应学习率算法确定网络的最优学习率,相应的MOb–GRU反向更新算法形式为

其中:W(·)代表MOb–GRU模型中需要学习的权重参数Wo,Wrh,Wrx,W˜hh,W˜hx,Wzh,Wzx,后面该变量含义与此保持一致;k为采样时刻;T为采样周期,设置T=1 min;i为反向更新单元数.为方便起见,后续形式上将采样周期T省略,即用k表示kT.

注1本文根据数据集的长度将其划分为n段,预选学习率由(n−2)个从小到大取值的固定学习率组成[α1,α2,···,αn−2],α1<α2<···<αn−2.

注2为保证网络训练时不会发散且使网络较快地达到收敛,本文将初始学习率设置为预选学习率数组中的中间数值.

3.2.2 学习率矩阵算法

Hessian矩阵[36–37]常用于优化问题,是用一个标量对一个向量的二阶导数组成的方阵.对于实际问题Hessian矩阵可能会很难计算,因此通常采用近似二阶Hessian 矩阵法代替计算,如BFGS 算法[38]、DFP 算法[39]与Levenberg–Marquardt(LM)算法[40].本研究将采用类LM算法作为学习率矩阵算法,利用近似二阶Hessian矩阵的逆的方法代替步长,对权重进行更新.该算法结合了梯度下降法和高斯–牛顿法的优点,使网络能较快且稳定地找到参数的最优值.

利用学习率矩阵算法对MOb–GRU网络参数进行反向更新时,算法形式如下:

注3两种学习率优化算法的区别在于:如果训练网络时已经能够确定基础步长的范围,则采用SAC自适应学习率算法;当无法确定基础步长范围时,采用学习率矩阵算法.SAC自适应学习率算法能够提高网络的整体运算效率,而学习率矩阵算法只需提前选择合适的阻尼项,便能对权重进行较好的调整,是能够保证神经网络达到收敛的一种较为稳妥的训练方法.

4 仿真实验

对于真实的工业过程,可以通过一个较快的采样频率采集过程数据,再进行神经网络建模.而本文给出带有输出非线性的仿真系统,是为了代替实际工业过程而产生过程数据,再根据所产生的数据对仿真系统进行建模.本节基于MOb–GRU软测量模型分别对单变量与多变量非线性动态过程的仿真系统进行模拟,旨在验证本文提出的MOb–GRU模型的有效性.在单变量非线性动态过程的建模中,讨论了关键网络结构参数以及系统波动程度对MOb–GRU训练性能的影响.另外,仿真时将MOb–GRU与RNN,GRU两个基线模型进行了对比,同时将SAC自适应学习率算法、学习率矩阵算法分别与固定学习率算法进行了比较.

4.1 单变量非线性动态过程的建模与预测

该实验中,单变量非线性动态过程的仿真系统可表示为

注4u(·)代表非线性动态过程的输入信号,作为软测量中的辅助变量,取为多正弦信号

其中:k为采样时刻;取采样周期T=1 min;本小节使用的数据集是通过式(8)–(9)仿真生成的,共81000个输入输出样本数据,以3:1:1的比例将数据集划分为训练集、验证集和测试集.x(·)表示中间状态变量;y(·)表示输出变量,作为软测量中的主导变量;w(·)表示过程噪声,是一种分布服从均值为0、方差为ϑ的高斯随机噪声,即

其中λ(·)表示参数的波动方差,后续实验中λ用于表示系统内部波动程度.λ越大,表示系统内部波动程度越大.

本小节静态非线性环节的具体表示如下:

MOb–GRU神经网络模型的超参数包括前向传播单元数、反向更新单元数以及预选学习率间隔.首先基于实验确定模型的关键结构参数.参数初始化设置如表2所示.

对于单变量非线性动态过程的仿真系统,考虑动态较为丰富且复杂的情况,将输入输出阶次ζ,η均设置为6;预选学习率间隔lrg暂时设置为0.08,即预选学习率为[0.08,0.16,0.24,0.32,0.40,0.48,0.56,0.64];式(5)中遗忘因子d设置为0.95;系统内部波动程度λ暂时设置为0.00152;外部波动程度ϑ暂时设置为4.02.为确定MOb–GRU的前向传播单元数j与反向更新单元数i,在验证集上进行对比实验,将MAPE作为评价指标,能够表征预测值与真实值之间偏差的实际水平,MAPE越小,模型性能越好.由于网络在训练过程中具有一定的随机性,每次训练得到的结果均有所不同,为保证实验结果的可靠性,对每组参数实验均进行50次重复,并将结果取平均,如表3 所示.其中:下标a表示采用SAC自适应学习率算法的网络训练结果;下标m表示采用学习率矩阵算法的网络训练结果;无下标表示采用固定学习率算法的网络训练结果.后面以表格形式呈现的实验结果同理.

表3 不同模型结构参数下的MAPETable 3 MAPE under different model structure parameters

从表3可见,在3种学习率优化算法下,前向传播单元数为19、反向更新单元数为6时,MAPE的值最小.当前向传播单元数小于19时,性能指标随前向传播单元数的增加而减小;当前向传播单元数大于19时,性能指标随前向传播单元数的增加而增加.这是由于当前向传播单元数增加到一定数目时,整个模型的参数爆炸增长,模型复杂度变大的同时预测精度降低.当反向更新单元数小于6时,性能指标随反向更新单元数的增大而减小;当反向更新单元数大于6时,性能指标随反向更新单元数的增大而增加,验证了当反向更新单元数接近模型阶次时,网络具有更好的性能.因此,将MOb–GRU模型的前向传播单元数设置为19,反向更新单元数设置为6进行后续实验.

进而基于实验确定合适的预选学习率间隔.在保证网络跟踪精度的基础上,lrg从0.01到0.3的范围内选取.在验证集上对每个lrg均进行50次实验,实验结果取平均,依旧采用MAPE作为评价指标.

如图4所示,对于[0.01,0.3]的预选学习率间隔而言,MAPE的值集中在0.0532∼0.0712之间.实验表明,预选学习率间隔过大或过小都会使MOb–GRU模型的训练性能变得相对较差,当lrg=0.19时,网络训练性能达到最优,此时MAPE=0.0532.因此本文将预选学习率间隔选为0.19,进行后续研究.

图4 MOb–GRU训练性能与预选学习率间隔的关系Fig.4 Relationship between training performance and lrg of MOb–GRU

为研究系统波动对MOb–GRU网络性能的影响,本文选择MAPE和均方根误差(root mean square error,RMSE)作为评价指标,RMSE由式(14)计算得到.为了对比模型的预测效果,选择RNN与GRU模型作为对比基线模型.为了验证本文所设计的两种学习率优化算法的有效性,将其分别与固定学习率算法进行比较

其中:L表示数据集长度;为网络预测输出;yc为系统真实输出.RMSE越小,模型训练性能越好.本文将系统波动分为系统内部波动与系统外部波动进行研究.基于以上实验,设置MOb–GRU结构参数j=19,i=6;GRU结构参数j=19,i=18;根据第2节的理论分析,设置RNN的结构参数j=2,i=1.

a) 系统内部波动对预测模型预测效果的影响.

系统内部波动是指动态线性环节参数向量的波动程度,每个参数可能具有不同的波动方差(如式(12)).设置式(8)中κ1=0.12,κ2=0.03,κ3=0.05,κ4=0.02,κ5=0.01,κ6=0.01,τ1=0.61,τ2=0.21,τ3=0.06,τ4=0.02,τ5=0.01,τ6=0.02以及系统外部波动方差ϑ=4.02.为研究模型预测效果与系统内部参数波动程度(用λ表示)之间的关系,假设所有参数的波动方差均相同,考虑如下几种情况:

对应不同的参数波动方差,实验分别进行50次重复并将结果取平均.在验证集上,运用MOb–GRU与两种基线模型分别对3种情况的非线性动态过程进行预测,表4给出不同模型在不同学习率优化算法下的预测结果.由表4可知,随着内部参数波动程度的增加,各模型在3种学习率优化算法下的预测精度均有所降低.原因是随着内部参数波动程度的增加,系统的随机性增强,在固定的网络参数设置下,易导致网络模型的预测精度降低,对实际系统的跟踪性能变差.

表4 不同系统内部波动程度下的MAPETable 4 MAPE under different degrees of internal system fluctuation

b) 系统外部波动对预测模型预测效果的影响.

系统外部波动是指高斯随机噪声的波动程度,即过程噪声的波动方差.设置内部波动程度λ=0.0012,考虑噪声波动程度ϑ分别为4.02,6.02,8.023种情况,在验证集上针对每种情况均进行50次独立重复实验并将结果取平均,结果如表5所示.由表5可以看出,在3种算法下,随着噪声波动程度的增加,各模型的预测精度均发生了不同程度的降低.原因是噪声的存在会导致系统的随机变化程度增加,且噪声波动程度越大,系统变化频率越大,导致在相同的结构参数下预测曲线难以跟上实际系统的变化,预测精度下降.

表5 不同系统外部波动程度下的MAPETable 5 MAPE under different degrees of external system fluctuation

基于上述分析,在测试集上,运用MOb–GRU模型与两种基线模型分别对参数λ=0.0012,ϑ=4.02的非线性动态过程进行预测,表6给出3种模型在不同算法下的预测结果,采用RMSE评价指标评价模型的预测精度.图5为测试集上3种预测模型采用SAC自适应学习率优化算法对单变量非线性动态过程进行模拟的预测曲线与真实曲线对比,取测试集中100个数据进行预测.由图5可知,当合理设置模型参数后,MOb–GRU的预测曲线更接近实际曲线,能更好地跟踪真实曲线的变化.从表6可知,在3种学习率算法下,相比于基线模型RNN与GRU,本文提出的模型具有更高的预测精度.这是因为RNN模型只有短记忆性,与长短期记忆模型MOb–GRU相比,无法捕捉长距离依赖关系,预测效果较差.本文将传统GRU模型的反向更新单元数设置得较多,使得整个模型的记忆范围变得较大,但与MOb–GRU相比,GRU计算量变大的同时预测效果反而变得不好.由此说明,反向更新单元数不是越多越好,当反向更新单元数接近实际过程的动态阶次时,预测效果更好.另外,在3种预测模型中,SAC自适应学习率算法与学习率矩阵算法下的预测结果均优于采用固定学习率算法所预测的结果,说明了本文设计的SAC自适应学习率算法与学习率矩阵算法的合理性.

表6 λ=0.0012,ϑ=4.02情况下3种预测模型的RMSETable 6 RMSE of three prediction models in case of λ=0.0012,ϑ=4.02

图5 3种预测模型采用SAC自适应学习率算法的预测曲线与真实曲线Fig.5 Predicted curve and real curve of three prediction models under SAC adaptive learning rate algorithm

4.2 多变量非线性动态过程的建模与预测

在单变量非线性动态过程的研究基础上,将其拓展为多变量非线性动态过程进行研究.本文考虑三输入单输出过程,该过程的仿真系统可表示为

其中:本小节用时间域的单变量高阶微分方程描述线性环节各通道的输入输出关系,系数ε1=1.5,ε2=2,ε3=1,β1=0.5,β2=0.3,β3=0.7;非线性环节用多项式形式表示;多变量非线性动态过程的阶次设置为1;本小节所用数据集通过式(15)(17)–(19)仿真生成,共生成81000个输入输出数据样本点,数据集划分同单变量非线性动态过程;ug(·)代表非线性动态过程的输入信号,作为软测量中的辅助变量,对于每个输入信号,均取为多正弦信号;xg(·)表示系统的中间状态变量;y(·)表示系统的输出变量,作为软测量中的主导变量;输入输出变量的采样周期T=1 min;w(·)表示分布服从均值为0、方差为ϑ的高斯随机噪声,即

考虑1个混频输入多变量非线性动态过程,即输入信号中含有低、中、高3种频率的正弦信号

预选学习率是以0.19为基础增量而构成的一个数组,设置噪声波动程度ϑ=4.02进行后续问题的研究.为了合理使用提出的MOb–GRU软测量模型,首先需要对MOb–GRU的结构参数进行确定,选择MAPE作为评价指标,进行网络训练性能的判断.与单变量非线性动态过程确定网络结构参数的实验一样,在验证集上进行对比实验,每组实验均进行50次并将结果取平均,经过9组对比实验后,最终确定MOb–GRU结构参数j=40,i=2;GRU结构参数j=40,i=39;根据第2节理论分析,设置RNN结构参数j=2,i=1.在测试集上,运用MOb–GRU模型与两种基线模型分别对混频输入多变量非线性动态过程进行预测,结果如表7所示.

在实验中,用到的计算机CPU主频为1.80 GHz,仿真软件为MATLAB R2020a.表8显示了3种预测模型分别采用SAC自适应学习率算法对混频输入多变量非线性动态过程进行训练的时间需求.由表7–8可知,相比于RNN模型,MOb–GRU模型提高了网络的训练性能与预测精度;相比于GRU模型,MOb–GRU模型在提高预测精度的同时还一定程度上减轻了网络的计算负荷.图6给出测试集上3种预测模型在SAC自适应学习率优化算法下的预测曲线与真实曲线,取测试集的200个数据进行预测.从图6可以看出,在存在高斯噪声的情况下,基于MOb–GRU软测量模型得到的估计值能更好地拟合实际值的变化趋势,具有更高的建模精度,说明MOb–GRU模型能够充分捕获数据中隐藏的信息,从而使预测运算能够达到更好的效果.

图6 采用SAC自适应学习率算法对实际过程模拟的预测曲线与真实曲线对比Fig.6 Comparison between predicted curve and real curve of the actual process under SAC adaptive learning rate algorithm

表7 3种预测模型的RMSETable 7 RMSE of three prediction models

表8 3种模型模拟所需的时间Table 8 Time required for three models’simulation

对比表6和表7可以得到图7所示结果,图7展示了用SAC自适应学习率算法进行训练时,MOb–GRU模型相较于传统GRU与RNN模型的预测结果对比.由图7可看出,当实际过程动态阶次较高时,从预测效果上更能体现MOb–GRU长短期记忆模型较GRU长短期记忆模型与RNN短记忆模型的优越性;但当实际过程动态阶次较低时,MOb–GRU模型与GRU,RNN的预测精度相差不多,而基于RNN预测所需的时间较少.综上所述,可以得到:1)实际过程动态阶次高→系统动态特性丰富→包含前面时刻的u,y多→所需存储空间较大→适合选择MOb–GRU模型→模型具有长短记忆性且能充分体现当前时刻与前面时刻丰富的非线性动态关系→性能优于长短期记忆的传统GRU模型与短记忆的RNN模型;2)实际过程动态阶次低→系统动态特性贫乏→包含前面时刻的u,y较少→所需存储内存较小→系统记忆性较短→适合使用短记忆的RNN进行处理.因此比较MOb–GRU与GRU,RNN时,需选取动态阶次高的非线性动态过程才更能体现MOb–GRU长短期记忆网络的优越性.

图7 MOb–GRU相较于GRU/RNN的预测结果对比Fig.7 Comparison of prediction results between MOb–GRU and GRU/RNN

5 结论

本文提出了一种依赖模型阶次的工业软测量网络模型—–MOb–GRU,介绍了MOb–GRU神经网络的训练原理、算法及流程,设计了两种学习率优化方法—–阶跃衰减类(SAC)自适应学习率算法与学习率矩阵算法.实验表明,记忆神经网络总的模块数与描述实际过程动态特性丰富程度的能力相关,每一个模块内部状态变量的维度与表示非线性的能力相关,设置好合适的参数后,神经网络能够包含复杂且充分的非线性动态特性,以上两部分共同完成了记忆神经网络对非线性动态过程的充分性建模.在输出预测任务中MOb–GRU的预测精度高于RNN与GRU模型,采用SAC自适应学习率算法和学习率矩阵算法的网络训练结果均优于采用固定学习率算法的训练结果,但MOb–GRU的泛化能力和适用范围有待进一步确定.未来作者将收集实际现场数据,利用自适应学习率或学习率矩阵算法对MOb–GRU软测量模型进行高效训练,并给出合适的输出预测以构造更多有效的虚拟样本.