基于动态参考规划的鲁棒Tube模型预测跟踪控制

陈 硕,郑年年,栾小丽,刘 飞

(江南大学物联网工程学院,江苏无锡 214122)

1 引言

作为一种比较先进且成熟的控制方案,鲁棒模型预测控制(model predictive control,MPC)现已被成功应用于各个领域[1–3].在RMPC(robust MPC)算法发展的过程当中,为加强有界扰动及约束作用下RMPC的鲁棒性及稳定性,Mayne等人在文献[4–6]提出一种基于Tube的RTMPC(robust Tube-based MPC)方法,该方法根据线性系统叠加原理,将不确定性系统的动态演进分解为标称状态动态和误差动态,控制作用中的标称分量保证标称状态的收敛性,而对受扰状态和标称分量之间误差的线性反馈则保证扰动带来的影响收敛于一个不变集中.随后国内外学者将RTMPC拓展到了非线性[7]、参数不确定性[8]、参数时变[9]、切换系统[10]等;同时考虑系统的资源约束问题,将自触发[11]、事件触发[12]等与RTMPC相结合;也有学者围绕经济优化目标问题,将RTMPC用于经济MPC[13]的研究.

上述关于RTMPC的研究成果主要针对以零设定点为跟踪目标的问题,但在实际工程应用中,目标值一般都设定在非零点处,因此需要在RTMPC的基础上进行优化与改良,设计一种更加灵活的控制方案,能够对目标值进行跟踪,使得被控状态在有噪声干扰下,收敛于以设定值为中心的区域.为了解决RTMPC的不足,很多学者提出了改良方案,如文献[14–16],其中Lim´on等人指出了这些改进方案的不足之处,并提出了一种分段常值跟踪MPC方法[17],该方法在设定值发生变化时,仍能保证系统状态收敛到以期望的设定值为中心的邻域内.之后,Lim´on等人结合文献[5]中所提的鲁棒Tube方法,将文献[18]的跟踪MPC拓展到有界扰动下的鲁棒跟踪[17].Lim´on等人在文献[17–18]中所采用的零空间参数本质上与标称系统的一组稳态(参考稳态)或参考输入相对应,在线优化以一步参考作为决策变量,由于每次在线优化只得到一组决策参数,即一步参考,导致控制器作用过强,当初始状态距离设定点较远时,容易丧失可行解.

本文受到Lim´on等人的启发,提出一种动态参考规划(dynamic reference programming,DRP)方法,并与RTMPC相结合,设计出一种新型的模型预测跟踪方案,将多步参考输入作为决策变量来设计控制器并实施在线滚动优化.多步参考输入一方面用于控制器设计实现对最后一步参考稳态点的跟踪,另一方面作为决策变量为在线优化提供了灵活的自由度,而约束满足和递归可行性保障都转化为对动态参考的约束来实现.另外,通过最小化标称预测轨迹和参考稳态之间的距离,同时惩罚最后一步参考稳态和设定点之间的距离,可确保闭环标称系统收敛于最优跟踪点,也即在设定点可达情况下实现零误差跟踪,在设定点不可达的情况下跟踪到距离设定点最近的允许位置.由于采取了RTMPC方案,实际受扰状态收敛到以最优跟踪点为中心的有界正不变集中,实现最优鲁棒跟踪.

2 问题描述

对于具有加性扰动的线性时不变系统,可用状态空间方程表示为

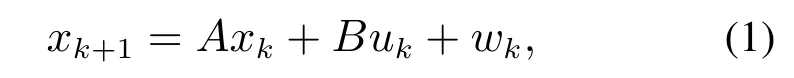
其中:xk ∈Rn表示在k,k ∈N[0,∞]时刻的n维状态,xk+1表示下一时刻的状态采样值,uk ∈Rm是m维的控制输入,wk ∈Rn表示系统受到的外部扰动,并假设任意时刻的扰动位于如下所述的凸多面体中:

其中W={w ∈Rn||wi|≤σi,i=1,2,···,n}.

另外,考虑系统(1)的状态和控制输入具有如下约束:

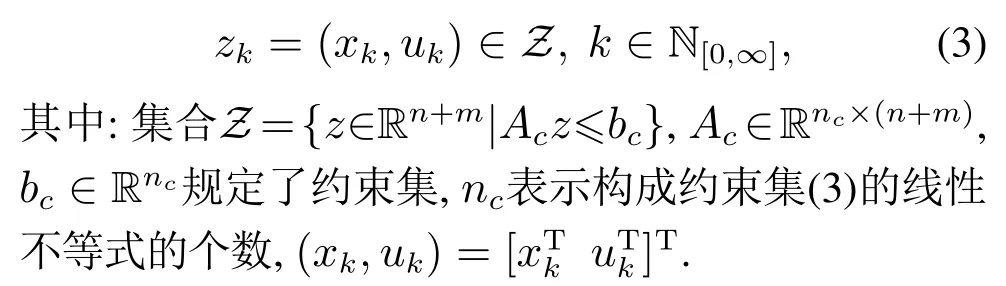
设计如下控制作用:

其中AK=A+BK.本文令AK为严格稳定,在此条件下,状态误差的演进是有界的,可以定义如下扰动不变集(disturbance invariant set,DIS)[5].

定义1对于一个集合E ∈Rn,如果对任意的e∈R以及任意的w ∈W,都有AKe+w ∈E,那么集合W是不确定系统(1)的一个DIS.

本文利用MPC方案实现系统(1)的跟踪问题,还需要考虑到在线滚动优化的递归可行性,因此本文RTMPC方案设计的具体任务和目的可以归纳为寻找控制作用,k≥0使得:I)保证约束条件(7)满足;II)保证在线优化的递归可行性;III)保证标称系统(5)收敛于.

3 基于DRP的跟踪控制

当标称系统(5)到达稳态时,存在如下关系:

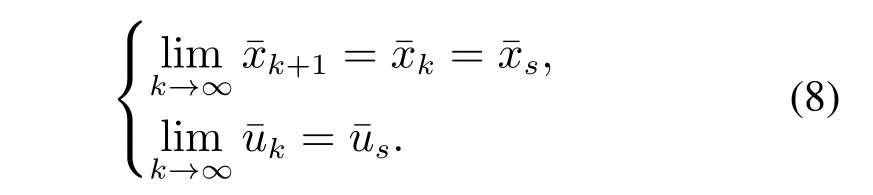
此时动态方程(5)退化为如下所述的代数方程:

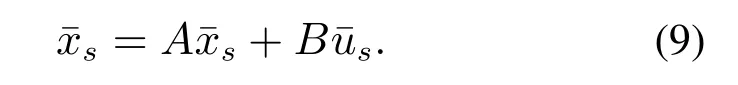
Lim´on等在文献[17]中将上述稳态关系表示为如下的方程组:

利用线性方程组的求解理论,该方程的解为

其中M为齐次线性方程组(10)的一组基础解系,因此每当参数θ确定,便有一组稳态与之对应,Lim´on等人基于此,设计了标称控制作用为

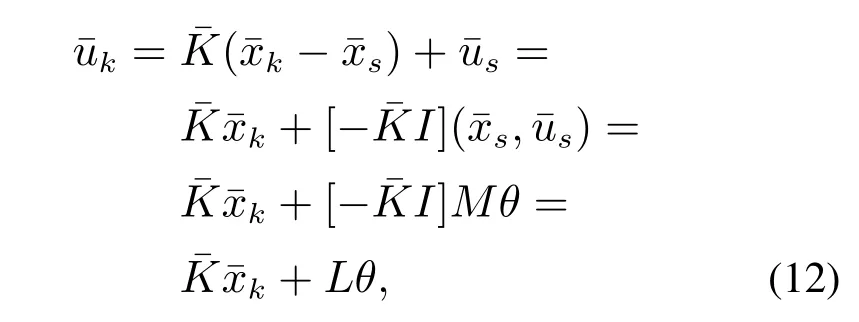
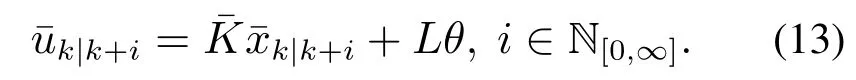
为了实现设定点的跟踪,本文对标称系统(5)施加如下控制作用:

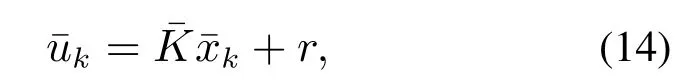
其中参考输入r决定了最终系统的稳态位置.假设是严格稳定的,则当系统最终到达稳态时,根据式(8),有

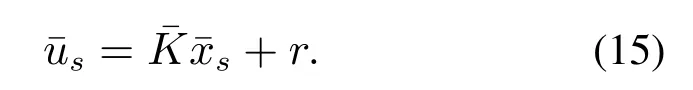
对比式(12)(15)可知

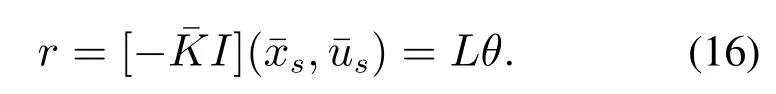
注1通过上述分析可以看出,Lim´on等人实施MPC优化的决策变量θ实际上是参考输入的一种等价表示,而每次优化寻找一组最优参数θ可以理解为寻找对应某个稳态的一步参考输入.

联立式(9)(15)可得

为了克服Lim´on等人方法的局限性,本文直接以参考输入为决策变量,在k时刻进行MPC优化时,令未来的控制作用为

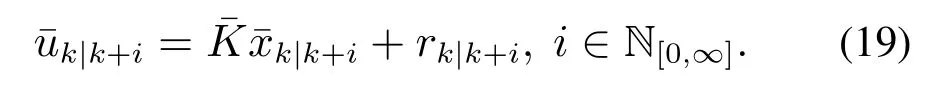
上式中的动态参考输入需要满足集合(18)的约束以及

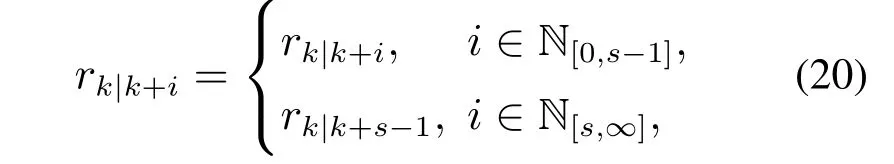
其中1 ≤s≤N被定义为优化时域.

注2本文以s步动态参考作为MPC优化的决策变量,相比于Lim´on等人的一步参考,步参考不仅可以增加MPC优化问题的自由度,而且能有效降低控制器负担.另外,当s=1时,本文提出的控制器退化为Lim´on等人所提控制器的一种等价形式.

标称系统(5)在控制律(19)的作用下所形成的闭环标称系统为

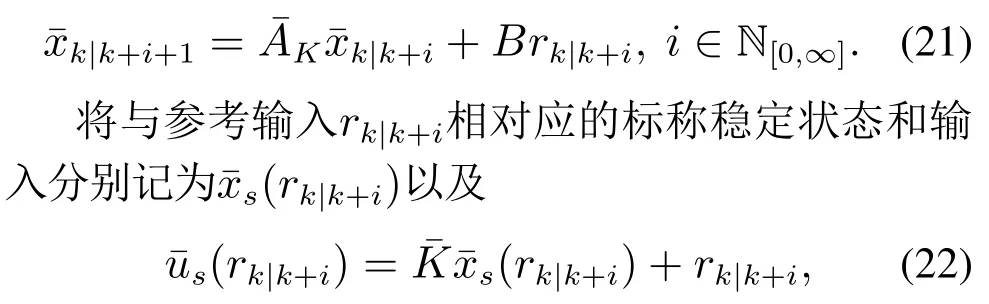
则关于闭环系统(21)有如下引理:

引理1闭环系统(21)必然收敛于稳态位置

证当时间趋于无穷时,标称系统(5)的状态可以表示为

4 基于DRP的RTMPC

根据第2小节的问题描述以及上一节提出的基于DRP的跟踪控制,可以设计基于DRP的RTMPC代价函数及约束条件为

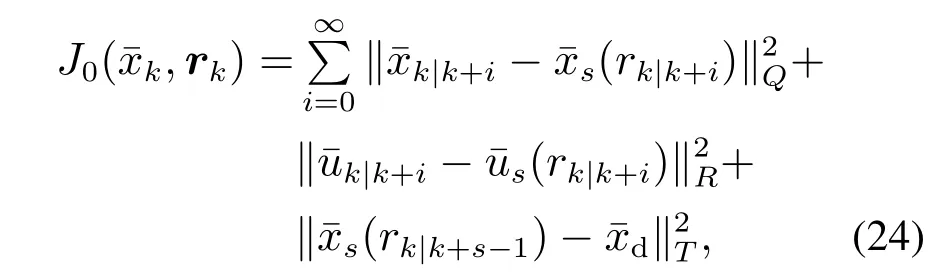
其中权系数矩阵Q,R,T为正定矩阵,其中阶段代价

定义2所给出的TIS中可以作为优化问题P0(,rk)的终端约束集,集合元素既包括了标称状态分量,又包括参考输入分量r,由引理1可知,如果以r作为最后一步参考,闭环系统(21)可收敛于r对应的稳定状态(r),因此定义2给出的TIS作用在几何上可以理解为:状态进入一个以(r)为中心的一个不变集,从该集合出发的任何一个初始状态,在以r为参考输入的状态反馈控制作用下,状态和输入轨迹都将满足约束(7),且状态和输入最终分别收敛于(r)和基于定义2,约束∈N[0,∞]可以转化为

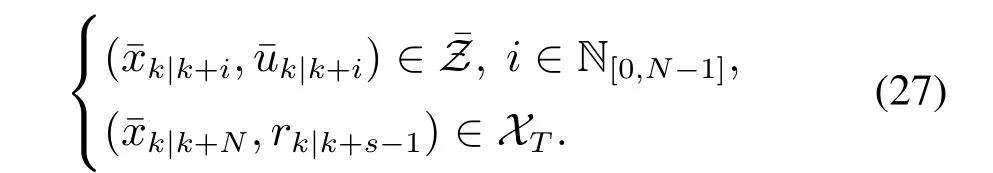
因此,优化问题P0(,rk)中的无穷项约束被转化为预测时域内的有限项约束和终端约束,使得优化问题可行.进一步地,对代价函数(26)中的参数进行设置.线性反馈取为线性二次型调节器(linear quadratic regulator,LQR)增益,其中Q,R为正定矩阵,令P为如下Riccati方程的解:

当参数τ足够大时,可以对闭环系统(21)收敛到的稳态(rk|k+s−1)和设定点之间的加权欧氏距离进行充分惩罚,从而任意降低二者之间的距离,引导系统(21)尽可能地跟踪.

根据式(25)可得如下推导关系:

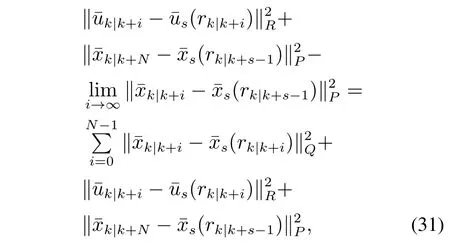
其中最后一个等号的得出根据引理1.基于上述结论,本节提出基于DRP的RTMPC跟踪目标函数为

算法1:基于DRP的RTMPC实现最优鲁棒跟踪

离线

第4步设置下一采样时刻为k=k+1,测量状态xk,返回执行第2步.

5 仿真验证

本文将所提的控制器设计方案应用到如下双重积分器模型:

其中状态和控制输入受到约束

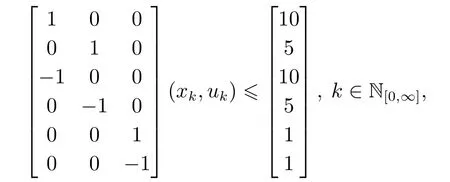
噪声位于如下凸多面体中:

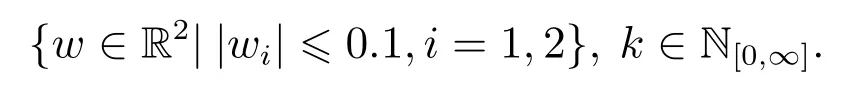
RTMPC方案中的相关参数选取为

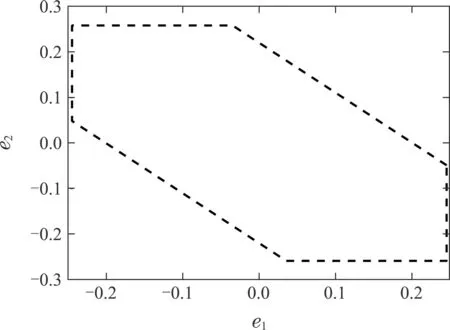
图1 DIS示意图Fig.1 DIS schematic

系统的TIS和RTIS如图2所示.

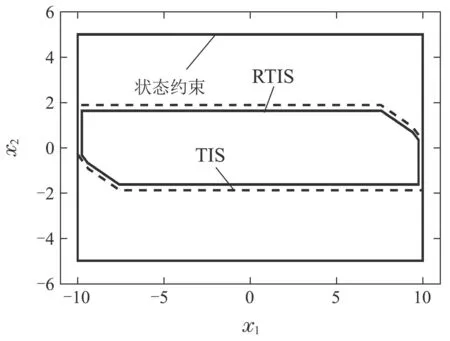
图2 TIS及RTIS示意图Fig.2 TIS and RTIS schematic diagram

图3(a)中每一步紫色多边形的大小和形状由DIS决定,位置则由每一步的标称状态决定,给定了每一步受扰状态所在的鲁棒Tube,限制了标称状态和受扰状态之间的距离范围,而该Tube收敛于固定的位置,表明状态最终收敛于以标称跟踪点为中心的DIS中.图3(b)可以看出不同扰动实现下,状态轨迹位于一定的范围内.

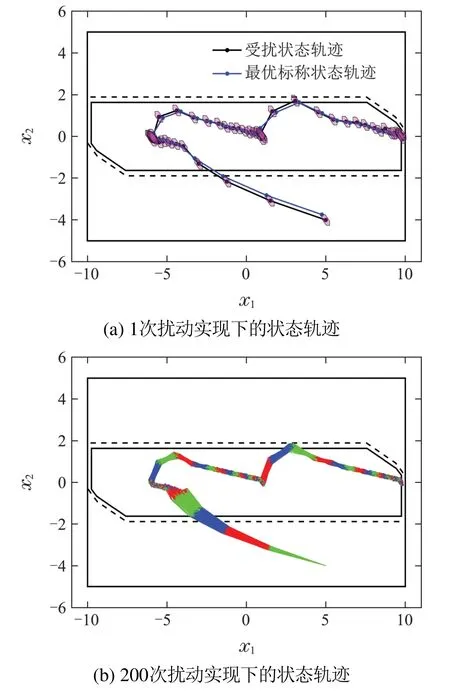
图3 状态响应轨迹Fig.3 State response trajectory

200次扰动实现下的状态终点分布如图4所示.

从图4可以看出,不同跟踪目标下状态均收敛于以标称跟踪点为中心的DIS中,当设定点可达的时候,标称跟踪点与设定点重合;当设定点不可达时,标称跟踪点位于TIS的边界上且距离设定点最近的位置,此时受扰状态所收敛的集合位于RTIS的边界,因此系统实现了最优鲁棒跟踪.

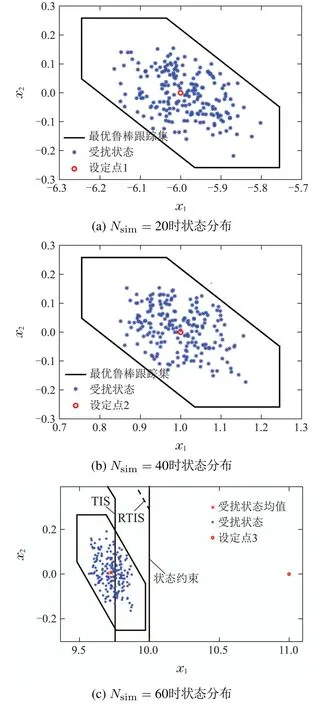
图4 不同跟踪目标下状态分布Fig.4 State distribution under different tracking targets

另外,为了对比优化时域s对本文所提跟踪算法的影响,在不同s设置下,图5给出了控制输入位置及增量的变化.

从图5可以看出,随着s的增大,每一步控制输入位置和增量都逐渐较小,也即当优化时域较大时,控制作用的幅度和变化都较小,进而验证了本文所提多步参考可以减轻控制器的负担.

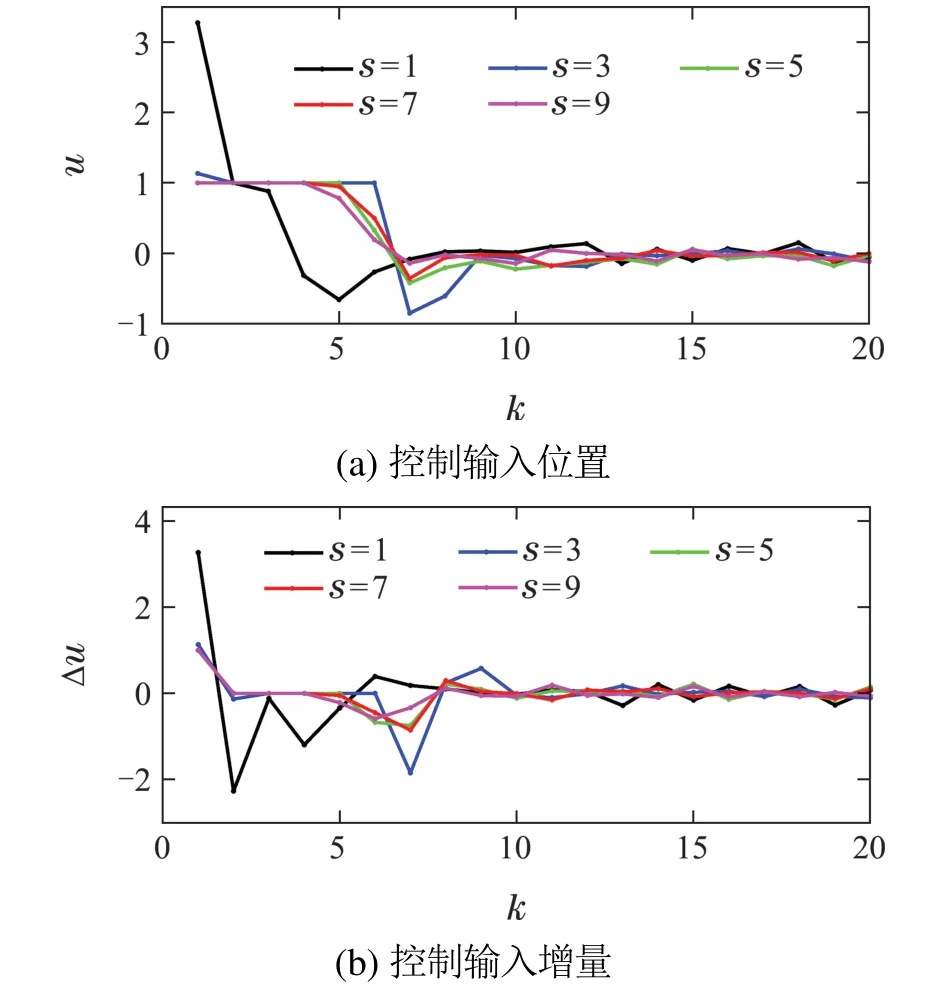
图5 不同优化时域下控制输入变化Fig.5 Control input changes in different optimization time domains

从表1可以看出,与Lim´on等人的一步参考比起来,多步参考输入可以令控制作用负担更小、每一步控制变化量更小,虽然同时也导致算法时间复杂度提升,但是从系统所消耗能量的角度来看,多步参考输入的系统能量平均值减少.

表1 不同优化时域下的平均能量Table 1 Average energy in different optimized time domains

为了验证控制方法的实用性,将本文所提RTMPC方法应用于如图6所示的DC–DC变换器电路.

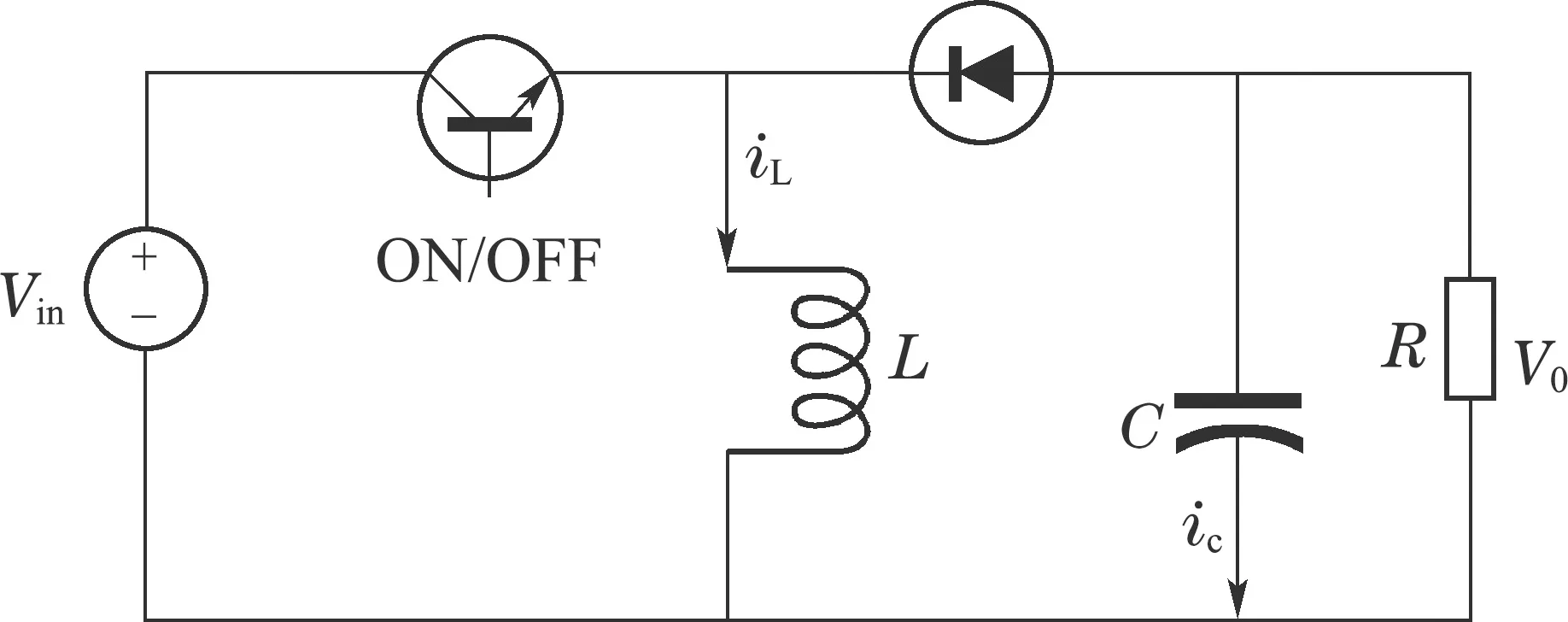
图6 DC–DC变换器的示意图Fig.6 Schematic of DC–DC converter

系统的状态约束集合为

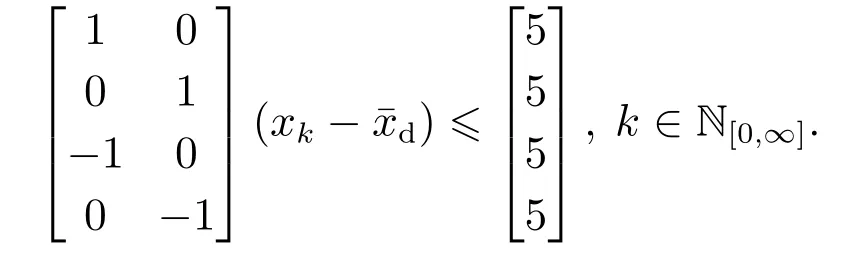
RTMPC参数选取为

从图7和图8可以看出,当本文所提方法用于DC–DC变换器时,可以有效实现电路状态的最优鲁棒控制,动态轨迹在鲁棒集合内,稳定状态分布在以设定点为中心的最优鲁棒不变集内.将本文所提方法与当前DC–DC变换器常用的状态反馈控制效果进行对比,如图9.

图7 200次扰动实现下的状态轨迹Fig.7 State trajectories under 200 perturbations

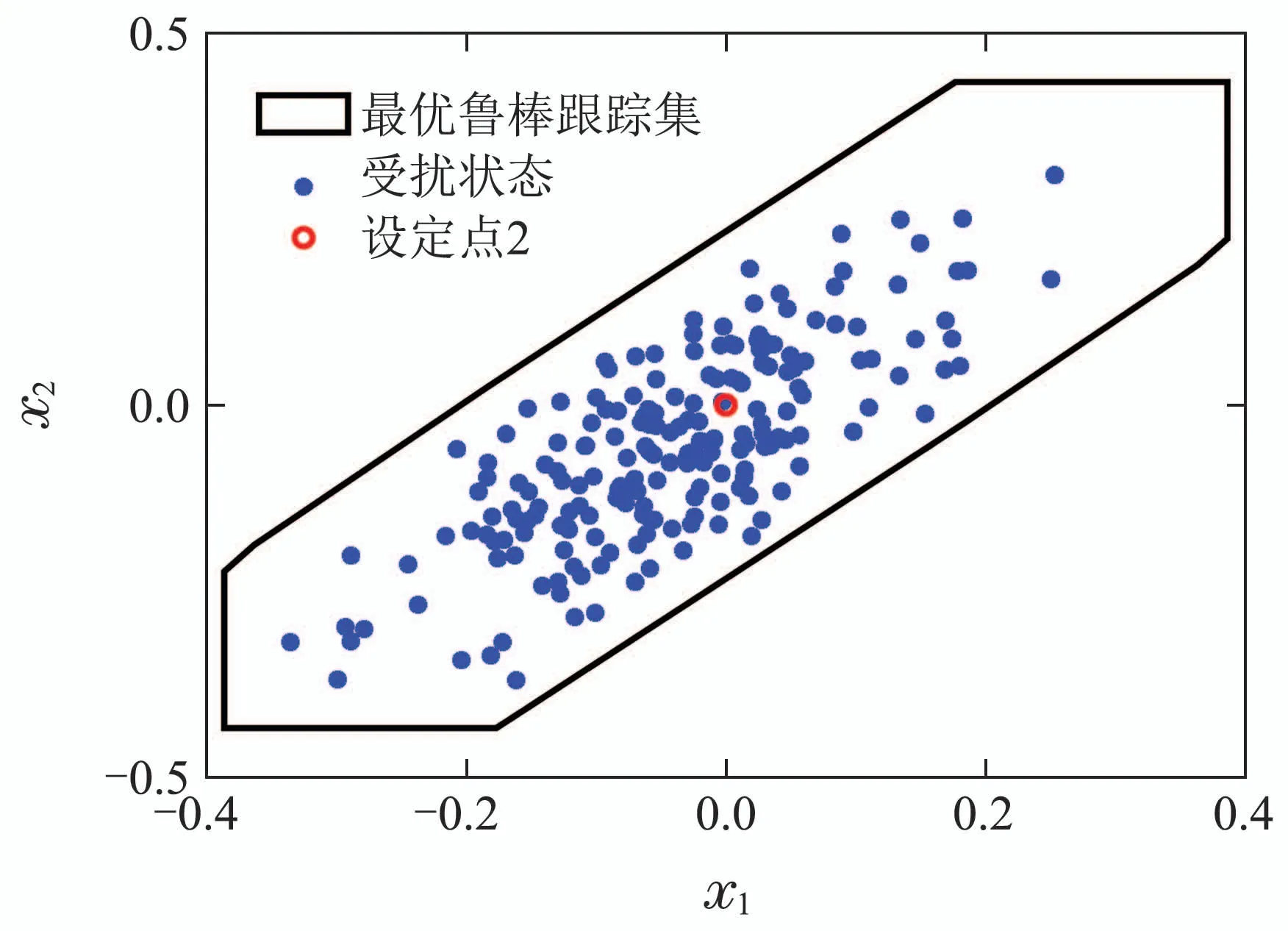
图8 Nsim=30时状态分布Fig.8 State distribution when Nsim=30

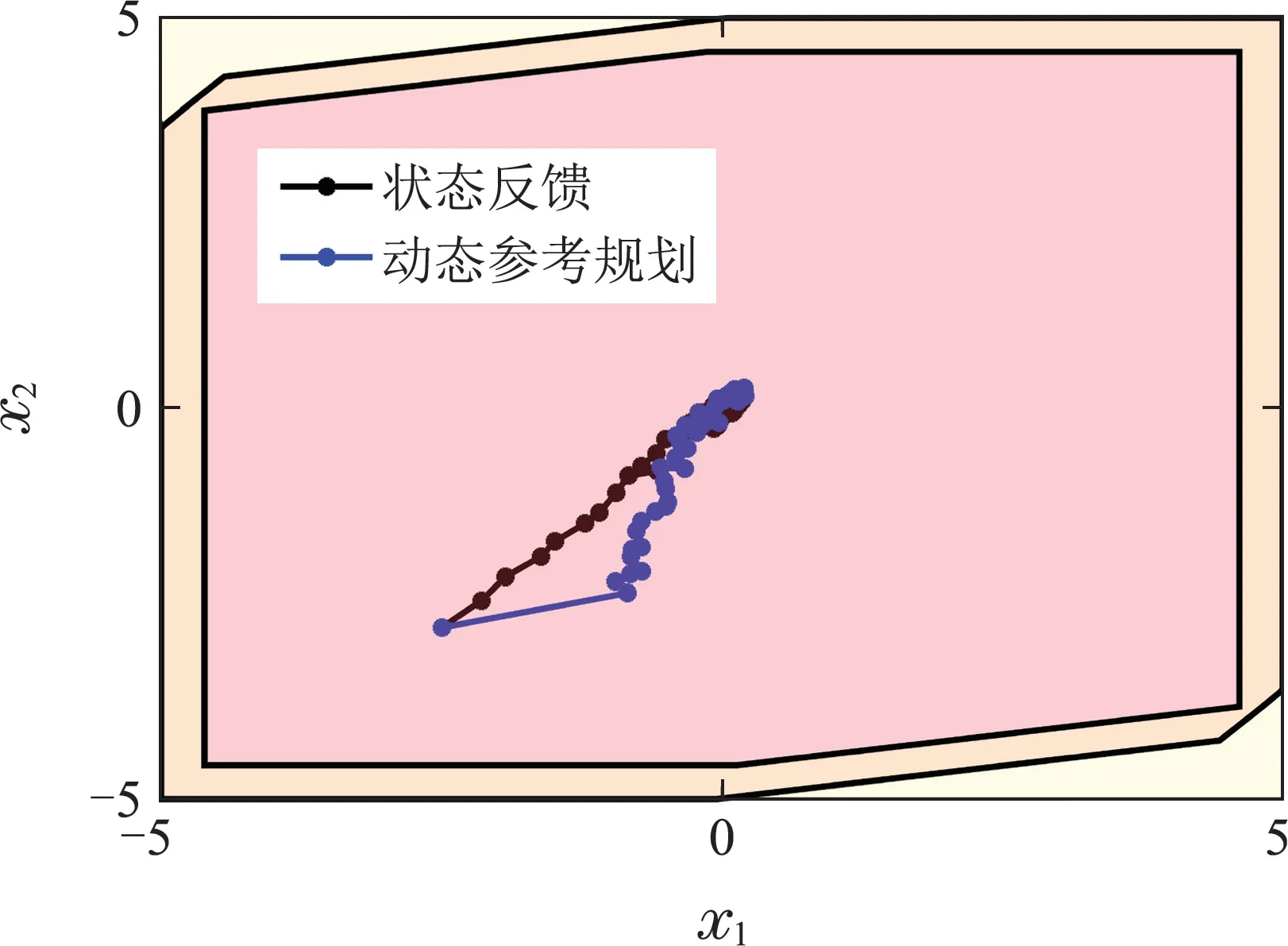
图9 状态反馈和动态参考规划的对比轨迹Fig.9 Comparative trajectories of state feedback and dynamic reference programming

从图9中可以看出,由于状态反馈控制本质上相当于参考输入为0的一步参考规划,动态参考规划方案能够在成功实现控制目标的同时,比状态反馈控制更为缓和,这也意味着控制作用负担会更小.

6 结论

本文提出一种基于DRP的RTMPC用于受到有界扰动系统的最优鲁棒跟踪,该方案将多步参考输入作为决策变量来设计控制器并实施MPC滚动优化.就在线优化求解而言,多步参考可以降低控制器负担,同时使得优化问题具有更灵活的自由度,当初始状态距离设定点较远时,可通过增大优化时域来保证约束满足以及可行解的存在.就跟踪性能而言,基于DRP的跟踪控制保证了闭环标称系统的收敛性,MPC目标函数则同时惩罚标称状态轨迹和参考稳态之间、以及最后一步参考稳态和设定点之间的加权欧式距离,确保受扰状态收敛到以最优跟踪点为中心的有界正不变集中,实现最优鲁棒跟踪.仿真结果验证了该控制器的性能及优势,可以实现被控对象的最优鲁棒跟踪.未来研究工作将结合系统的概率特性,研究基于DRP的随机MPC跟踪方法.