基于参数估计误差的辊道窑温度场优化控制方法

陈 宁,李彬艳,赫学实,罗 彪,桂卫华,阳春华

(中南大学自动化学院,湖南长沙 410083)

1 引言

锂离子电池正极材料具有能量密度大、循环寿命长、安全性能好等优点,已广泛应用于智能手机、电动汽车等多个领域,成为当今应用最广泛和最有发展前景的电池材料之一[1].锂离子电池最重要的组成为正极材料,锂电池需求的日益增加使得开展正极材料制备过程的研究对于提高材料产品一致性意义重大.烧结过程是制备过程最重要的工序,主要在工业辊道窑中进行,国内外对工业辊道窑热处理过程的建模及优化控制等方面进行了大量研究.

辊道窑烧结过程是一个复杂、非线性、强耦合的过程,同时也是一个连续缓慢发生化学反应的长过程[2].为了对辊道窑内部的温度与浓度进行估计,文献[3]通过对加热电阻炉各段施加控制信号来观测炉内各段温度的阶跃响应,并采用阶跃响应法建立了考虑纯时滞下的辊道窑加热系统数学模型.上述方法是当前研究辊道窑炉内温度普遍采用的建模方法.文献[4]从温度和总能量的角度,把温度当作集中参数考虑来处理,通过合理的简化得到一阶含纯时滞的数学模型.虽然上述方法可以预估温度,但由于进行了大量简化使得温度估计值与真实值之间存在较大的误差.所建立的模型与实际过程相比存在较大差异,模型的精度一般无法满足要求.为解决上述难点,从过程机理出发,开展辊道窑温度场建模研究,对烧结过程的优化控制具有重要意义.

工业窑炉内温度场和浓度场等物理场的机理建模研究可以为本过程的建模提供有益的参考.文献[5]根据传热理论对热风炉的速度场和流体场开展研究,得到了气流速度场、CO密度场的分布结果.文献[6]在建立连续退火炉的模型时综合考虑了炉子部件的辐射传热和对流传热,进一步提高了模型准确度.文献[7]在大型立式淬火炉中采用简化区法计算了辐射热通量,提出了一种新的双外推有限元法求解工件的瞬态温度场.上述建模方法能够直接显示物理场的分布,对分析物理场的变化特征非常有益.但是,该类方法的求解一般需要依赖数值仿真软件,求解复杂且耗时长,往往难以用于实际工业过程.

为了提升三元正极材料产品一致性,需要对辊道窑烧结过程的温度场进行优化控制研究[8].对于复杂工业系统优化控制问题,求解方法主要为基于梯度理论的优化方法,如最速下降法、共轭梯度法及非线性规划方法等[9–11].这类方法原理简单易于实现,但由于属于局部搜素方法,其寻优结果受初始值的影响很大[12]且无法保证算法的收敛性,还要求所用的过程模型显式可导.基于模型的控制方法在实际应用时由于面临不确定性、干扰等问题难以取得较好的控制效果,无法为本文的控制研究提供有益的参考.在上述困难下,基于数据的强化学习优化控制方法的相关研究应运而生.

1957年,美国学者贝尔曼为求解最优控制问题提出了贝尔曼最优性原理,该最优控制问题的解满足哈密顿–雅可比–贝尔曼(Hamilton-Jacobi-Bellman,HJB)方程[13].自适应动态规划(adaptive dynamic programming,ADP)作为强化学习方法的主要代表,是一种按照时间正向顺序求解动态规划问题中HJB方程的方法[14–15],能有效处理非线性约束,求解效率较高.文献[16]提出了基于近似动态规划的在线无模型自适应控制方法,通过引入ADP求解最优控制问题,有效解决了具有未知动态的线性系统离散域和连续域最优控制问题.文献[17]提出了一种近似策略迭代(policy iteration,PI)方法,通过使用系统真实数据设计了一种基于最小二乘的加权残差方法,实现了无模型非线性最优控制.针对分布参数系统的优化控制,文献[18]提出了一种模型部分未知的偏微分方程(partial differential equation,PDE)系统在线自适应最优控制方法,并引入PI对HJB方程在线求解;文献[19]通过采用加权残差法和同步更新策略来近似哈密顿–雅可比–伊萨克方程的最优解,实现了H∞控制器的优化设计.

目前,神经网络的权值更新策略一般选取梯度下降算法或者最小二乘法等,这种参数估计方法的准确性大多依赖于观测/预测器的性能.在闭环反馈控制的研究中,常常采用将控制误差作为控制器的输入来减小控制误差的思想.这种思想近年来开始被引入到参数估计方法中.如文献[20]通过改变观测器设计和结构提出了一种有限时间内的收敛参数估计方法,可以增强参数估计误差的收敛性.文献[21–22]研究了一类基于参数估计误差修正的鲁棒自适应律设计方法,并将其应用到ADP中[23–24].上述方法极大地激发了本文的研究兴趣.然而,如何设计一种适用于分布参数系统的基于参数估计误差的ADP的NN权值自适应更新方法,在保证系统稳定性的情况下实现有限时间内NN权值的快速收敛和权值逼近误差的降低,具有一定的挑战性,同时也是一个亟待解决的问题.这也是本文研究的重点.

本文在根据传热机理建立辊道窑二维多孔介质能量守恒模型的基础上,引入角系数来构建反映热辐射作用的边界条件;考虑到竖直方向温度变化远大于水平方向,通过边界转换提出一种辊道窑一维温度场的建模方法.然后,在ADP的框架中,研究一种基于参数估计误差的PI参数更新方法,来对烧结过程的温度场进行优化控制研究,该方法可以有效保证评价网络权值的快速收敛.

2 辊道窑烧结过程温度场建模

正极材料烧结过程使用的设备为辊道窑.辊道窑由升温段、恒温段和降温段组成,各温段包含多个子温区,如图1.

图1 辊道窑单一温区内部结构Fig.1 Structure of a temperature zone in roller kiln

炉内包含加热系统、传动系统和进排气系统.加热系统采用电热式硅碳棒加热元件,通过调节通入的电流来控制其温度,以保证材料反应过程所需的温度.传动系统由紧密排列的辊棒构成,匣钵(盛放原料的区域)通过辊棒以缓慢的速度向前稳定地传送.进排气系统由进气孔、排气孔构成,分别用来排出烧结过程的废气和经由鼓风机向窑内通入所需的气体,以保证窑炉内部所需的气氛.窑炉内部的温度分布是材料烧结过程的关键,工艺要求各温区匣钵区域的温度尽可能逼近烧结制度中的温度设定值.

建模之前做出如下假设:1)不计炉壁的散热;2)不计流体的热辐射与热损失;由于气体通入速率恒定,且硅碳棒热辐射作用带来的温度变化远大于炉内气体热对流,故主要研究硅碳棒温度变化对炉内温度场的影响.3)忽略原料间摩擦带来的能量损失;4)钵体运动速度为1.6 m/h,可视为静止状态.由于匣钵区域发生材料制备过程的主要反应,以该区域二维截面为研究对象建立温度场模型,如图2.该区域可视作为由多孔介质组成的近似封闭系统,热量传递符合能量守恒定律.因而,匣钵区域温度场满足多孔介质下的能量守恒方程[25]:

其中:T为匣钵区域温度;t为时间;ρ1和c1为固体的密度和比热容;ρ2和c2为气体密度和比热容.ρ3c3=(1−γ)ρ2c2+γρ1c1,k3=(1−γ)k2+γk1,vw与vz分别为气体在w轴和z轴方向上的速度,k1为固体的导热系数,k2为气体的导热系数,ST为匣钵区域的内热源,γ为孔隙率.由于硅碳棒的热辐射带来的热量比气体的热对流大,因而在边界条件的构造中主要考虑硅碳棒的热辐射作用;考虑匣钵上/下表面仅受上/下硅碳棒放热影响,左右侧面同时受上下硅碳棒影响.根据传热定律构建如下边界条件:

其中:Qa,b是a对b的投射辐射,Qa是a的有效辐射.根据式(7),有限表面A2对微元表面dA1的角系数为

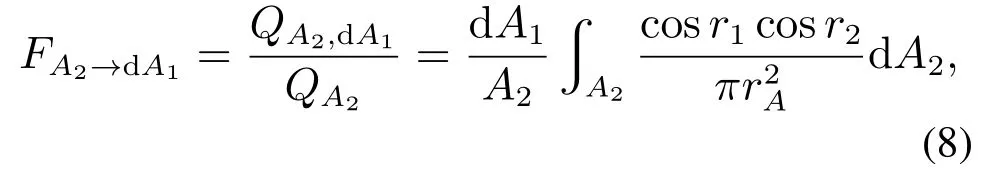
其中:rA是A2到dA1的距离,r1和r2为A2到dA1中心连线与其法线的夹角.

根据式(8),表面A2对于A1的角系数可表示为

根据式(8)和式(9),以硅碳棒p2为例对角系数进行计算,可以得到硅碳棒分别对匣钵上表面、对左侧面任一微元面的角系数,如下式所示:

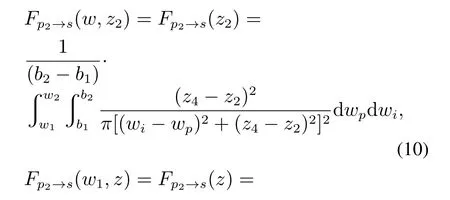
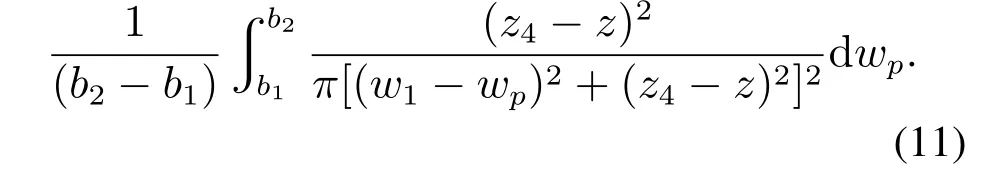
采用同样的方法可以计算硅碳棒p1对匣钵下表面的角系数Fp1→s(z1)和对右侧面任一微元面的角系数Fp1→s(z).

由如图2可知,辊道窑匣钵区域布局方式沿水平方向具有对称性.开展匣钵区域的建模研究时,可将其沿方向切割,仅对二维截面的一半区域进行研究.由于匣钵区域水平方向的温度变化非常小,相比之下竖直方向的温度变化更明显,即

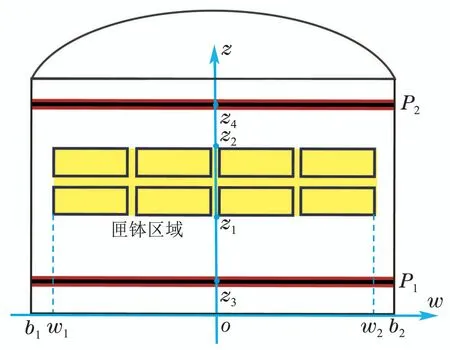
图2 匣钵区域结构图Fig.2 Structure of saggers area

[27].因此,可以将方向的温度梯度视为常值,通过引入式(1)来建立辊道窑温度场模型.该模型能够表征烧结过程控制输入与温度场的关系.以匣钵左半区域为例建立温度场模型.在这种情况下,式(1)中方向的温度梯度变化满足式(4)和式(6).将式(4)和式(6)代入式(1)可以对辊道窑温度场二维模型进行化简,进而得到一维温度场模型

3 烧结过程温度场的控制问题

为便于控制器设计,对所建立的模型(式(12))进行无因次变换.辊道窑温度场的控制目标为:使稳定后匣钵实际温度接近温度设定值Td(z),且尽可能降低实际值与设定值之差.基于此定义如下无因次的状态y(z,t)和控制变量u:

由于ε极小,引入τ=t/ε为快系统常数且让ε=0,则xf(t)=0.式(23)可以转换成有限维的低阶慢子系统,即

式中λi为KL分解中所涉及的矩阵特征值,0<ζ <1为一正常数.

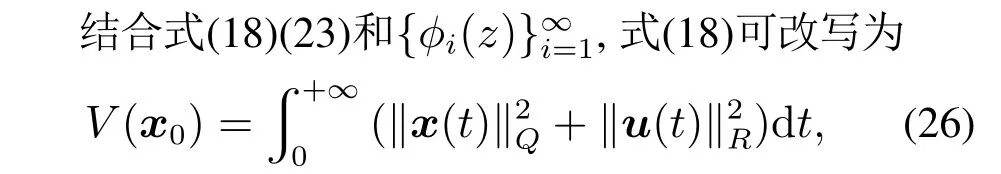
其中:Q=.Q和R均为正定对称矩阵.由此可将温度场的最优控制转化为低阶慢子系统的最优控制,并构建慢子系统的最优控制问题.

4 基于ADP的辊道窑温度场最优控制方法

本节提出一种基于参数估计误差的ADP评价–执行网络的参数辨识方法,然后开展辊道窑炉内温度场的优化控制研究.

4.1 基于模型降阶的最优控制问题

根据式(26),定义哈密顿函数为

基于慢子系统(式(24))及性能指标(式(26))的最优控制问题可以转化为求解HJB方程,即

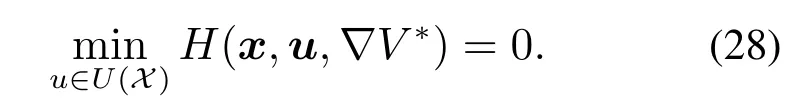
根据一阶最优性原理[29],可以对最优控制律进行推导,如下式所示:

将式(29)代入式(28),HJB方程改写为

其中对于V ∗(x)满足V ∗(x)∈C1(X),V ∗(x)≥0,且V ∗(0)=0.同时,V ∗(x)与Vu∗(x)存在如下关系:

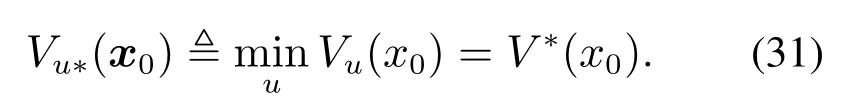
本文在容许控制无约束的情况下对PDE系统的控制律进行设计.对于容许控制为闭集情况,控制律的设计属于一类更深层次的控制器设计问题,是今后可以进一步深入研究的内容.由于HJB方程(式(30))为非线性方程,且降阶系统(式(24))中存在未知部分,理论上无法解析求解.为了克服这一困难,引入PI方法并基于过程数据在线求解HJB方程.采用PI算法求解HJB方程的步骤如下:

步骤1给定一个初始控制策略u0,i=0;

步骤2使用控制策略ui求解方程:

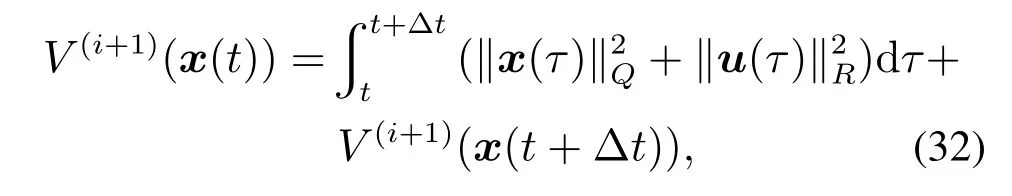
其中V(i+1)为待求解的代价函数;

步骤3通过式(29)更新控制策略获得ui+1;

步骤4令i=i+1,返回步骤2.

4.2 基于参数估计误差和策略迭代的温度场优化控制方法

PI算法的每一次迭代均需要对式(32)进行求解.为便于算法执行,采用一种评价–执行网络的结构,其中评价网络采用NN技术,用于逼近代价函数,同时,在利用评价NN逼近代价函数的过程中,提出一种基于权值参数估计误差的NN权值学习算法;执行网络则用于逼近控制策略.

评价NN用来近似最优代价函数V ∗(x),V ∗(x)可以精确表示为

由于真实的评价NN权值向量往往是未知的,因而评价NN的实际输出为

为设计基于参数估计误差的自适应律,运用已知的系统信息提取蕴含未知参数估计误差的信息.根据式(34)构建辅助矩阵P和辅助向量O,如下式:

其中η6>0为自适应增益.由于P−1O=KO=θ∗,式(43)能够直接反映参数估计误差的信息.换言之,本文所设计的ADP框架下的评价NN权值更新过程直接依赖于权值估计值与最优值的误差(即参数估计误差).这与ADP的传统参数更新方法不同,避免了对过程输入输出信息的直接使用.

然后,对执行网络进行设计.那么,根据式(29)和式(43)可得,执行网络的输出可由式(44)给出

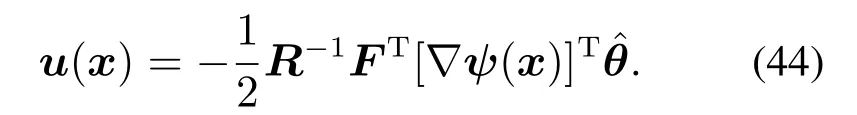
在此基础上,分析在所提控制方法下闭环PDE系统的稳定性.在此之前,给出如下假设.

引理1考虑由式(37)所设计的辅助矩阵P,那么,矩阵P为正定矩阵.换言之,矩阵P满足λmin(P(t))>δ1,对于t>0 和δ1>0[21].

定理1对所研究的PDE系统(式(12)),采用ADP方法实现其最优控制.如果矩阵正定,评价NN的权值参数自适应更新律如式(43)所示.那么,评价NN的权值估计误差在有限时间内收敛,即∥∥≤η8,且η8为一个大于0的小常数.

证构建如下李雅普诺夫函数V():

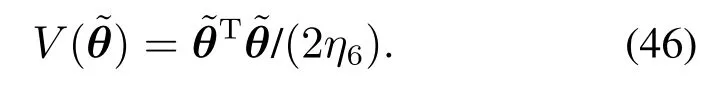
将式(43)代入式(46)中,同时对V()进行求导,并结合式(42)中的关系,可以得到

在此基础上,需要进一步证明在权值更新律式(43)和控制律式(44)下,低阶系统式(24)和原PDE系统式(12)的稳定性.

定理2对于温度场PDE系统式(12),如果假设1成立,选择初始权值θ0使得u0∈U(Ω),采用的权值更新律如式(43)所示,设计的控制策略如式(44)所示.那么,存在正常数η10,η11和ε∗,当∥x0∥≤η10,∥xf0∥≤η11和ε ∈(0,ε∗)时,使得x,xf和满足半全局一致最终有界(SGUUB),并且闭环PDE系统式(12)同样为SGUUB.

在证明之前需要对PDE系统进行改写,并提供相关条件.根据式(43)和式(44),式(12)可改写为

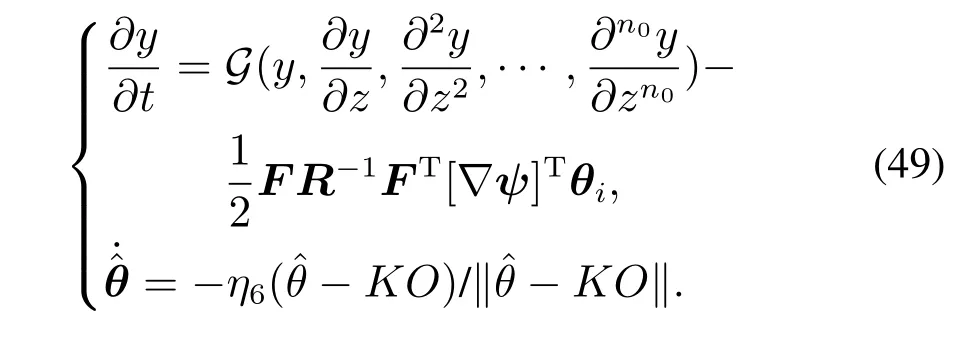
基于模型降阶方法,将式(49)改写为如下形式:

由于G为充分光滑的向量函数,那么存在一常数L0>0,使得如下不等式成立[31]:

式中L1–L6均为正实数.

在考虑稳定性之前,还需要推导如下条件:

5 仿真验证

本节对所提的温度场建模方法和优化控制方法进行仿真验证与分析,以证明所提建模方法的准确性和所提控制方法的有效性.

以辊道窑窑炉底部边缘的中心为坐标原点建立的直角坐标系如图2所示.

辊道窑烧结过程的相关物性参数与坐标参数分别为:密度ρ1=1.225 kg/m3,比热容c1=1006.43 J/(kg·K),导热系数k1=0.0242 W/(m·K),密度ρ2=2719 kg/m3,比热容c2=871 J/(kg·K),导热系数k2=202.4 W/(m·K),孔隙率γ=0.005,辐射率εp1和εp2为0.7,εs=0.3,流速vw=0.0476 m/s,vz=0.003 m/s.匣钵左表面的坐标w1=−0.675 m,右表面坐标w2=0.675 m,下表面坐标z1=0.35 m,上表面坐标z2=0.59 m;下部硅碳棒的高度z3=0.1 m,上部硅碳棒的高度z4=0.78 m,硅碳棒的左边界b1=−0.765 m,硅碳棒的右边界b2=0.765 m.

5.1 模型验证与分析

以第四温区为例,建立烧结过程温度场模型,并给定匣钵区域初始温度为T0=490◦C.首先,验证并分析所建立的模型在开环状态下的变化趋势.图3为所建立的温度场模型在开环状态(即不加热)下的温度变化曲面.由图3可知,匣钵区域温度呈逐渐下降的趋势,符合自然冷却下温度场的变化特征.

图3 开环系统状态Fig.3 The state of an open-loop temperature field

然后,选取实际过程某一时间段内加热功率基本恒定的情况下辊道窑的上部、下部测温点的实际数据来验证模型的准确性.给定匣钵上半区域的初始温度为680◦C,下半区域的初始温度为640◦C.同时,将上部、下部硅碳棒的温度分别控制在800◦C与725◦C左右,根据所建立的模型可以获得匣钵区域温度场的分布及演化过程.上部、下部测温点的温度预测值与真实值的比较如图4和图5所示.

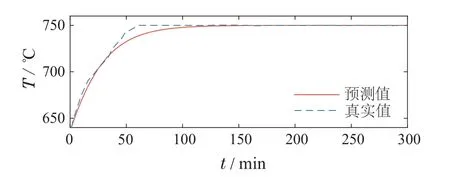
图5 下测温点温度预测值与真实值的比较Fig.5 The comparison between the predicted and true values of the temperature at the lower measurement point

由图4–5可知,升温过程测温点的温度预测值与实际过程数据的差值随着温度的逐渐稳定而越来越小,最后收敛至同一温度值附近.这表明所建立的模型能够准确模拟温度变化趋势,与实际温度变化过程匹配,准确性较好.这可以为三元正极材料烧结过程温度场的优化控制奠定良好的基础.

图4 上测温点温度预测值与真实值的比较Fig.4 The comparison between the predicted and true values of the temperature at the upper measurement point

5.2 控制方法验证与分析

将所提的温度场优化控制方法用于模型(12),以验证所提方法的有效性.

首先,给出该烧结过程的控制目标,即将匣钵区域的温度控制到520◦C.然后,通过设置=1000,根据式(13)–(14)对模型式(12)进行无因次变化,可以得到无量纲的PDE系统状态,例如图3可以通过上述变换等效转换成图6.接着,采用KL分解对模型进行降阶处理,选取ζ为0.001.对应的空间基函数ϕ(z)如图7所示.

图6 无因次变换后系统状态Fig.6 PDE system states after the dimensionless transformation

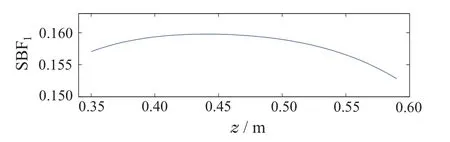
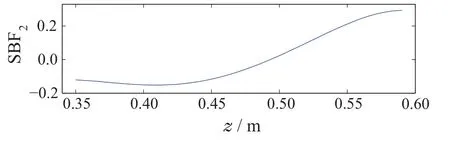
图7 空间基函数Fig.7 Spatial basis functions

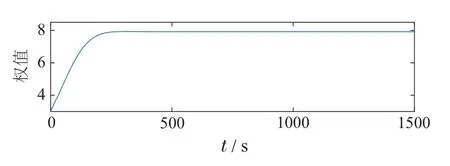
图8 评价NN的权值范数Fig.8 The weights norm of critic NN

图9给出了控制策略u(x)的变化曲线,其最终会收敛到0.图10为闭环低阶子系统的时间模态x(t)的轨迹,闭环PDE系统的状态曲面如图11所示.

图9 控制策略Fig.9 The control strategy

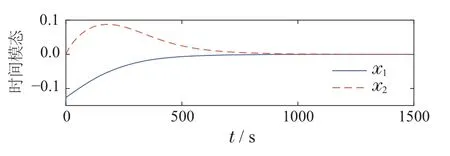
图10 闭环控制下的时间模态Fig.10 Time modes under the closed-loop control

图11 闭环PDE系统的状态Fig.11 The state of the closed-loop PDE system

由图10–11可知,低阶时间模态最终会收敛到0,温度场PDE系统的状态最终接近控制目标Td,且与温度目标值之差较小.这基本符合烧结过程控制要求,表明了所提优化控制方法的有效性.基于参数估计误差的权值更新方法与基于梯度下降法的参数更新方法[17]的对比如图12.选取基于梯度下降法的参数更新律的自适应增益为1.0.由图12可知,基于参数估计误差的权值更新方法收敛速度更快.在这种参数估计方法下,温度场达到控制目标所需时间进一步减少.综上所述,仿真验证结果表明了本文所提优化控制方法的有效性.

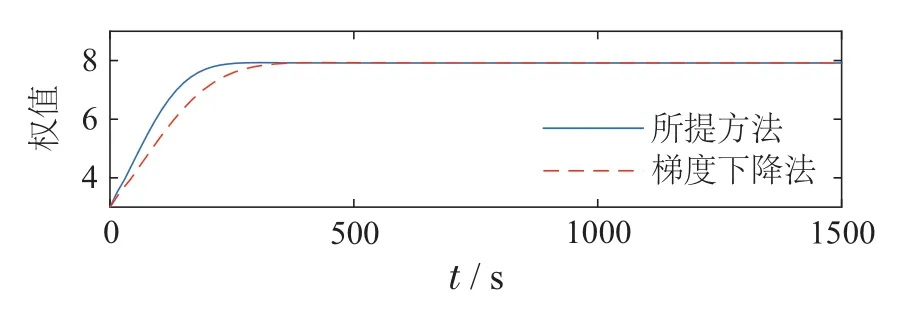
图12 权值更新方法的对比Fig.12 The comparison of weight updating methods

6 结论

本文主要研究辊道窑温度场的建模及优化控制方法.一方面,在分析辊道窑内部传热机理的基础上,根据能量守恒定律建立了辊道窑温度场模型;另一方面,在ADP的框架下,提出了一种基于参数估计误差的评价NN权值更新算法,在保证待估计参数快速收敛、减小权值逼近误差等基础上逼近最优代价函数,进而获得最优控制律.仿真验证结果证明了所提方法的有效性.上述方法的研究不仅可以有效解决当前窑炉烧结过程炉内温度分布难以获取、控制输入无法及时调整等制约正极材料产品品质提高的难点,也能为其他类似的工业过程温度场的建模及优化控制研究提供有益的参考.