一维反应扩散方程的参数辨识和源项反演

赵志学,郭宝珠,韩忠杰

(1.天津师范大学数学科学学院,天津 300387;2.华北电力大学数理学院,北京 102206;3.天津大学数学学院,天津 300354)

1 引言

对于物理学、化学以及生物学中的诸多问题,为了对它们进行定性、定量研究,就要建立各种数学模型,其中大量的数学模型都可以归结为反应扩散方程.实际上,工业中的许多控制都是控制温度.此外,外来物种的入侵以及大气、地下水污染等问题也都是典型的反应扩散问题[1–2],对此都可以通过建立相应的反应扩散模型来研究.

反应扩散方程的标准形式为ωt=∆ω+f(ω),方程右端表示两个物理过程的结合,其中第1项为扩散项,第2 项为反应项.对于这类方程的正演问题,相关研究成果很多,并且在化学化工、热流模型以及种群动力学等领域有着广泛的应用.然而,对于从实际问题中建立起的数学模型,系统控制方程中的参数通常是未知的,源项以及初始值也可能难以直接测量.因此,如何借助于一些易于测量的数据,通过设计算法或发展相关技术对这些未知量进行识别和确定,成为一类具有重要研究意义的课题.

当反应项为ω的线性函数时,反应扩散方程可用如下抛物型方程来描述:

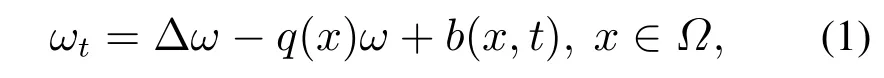
其中:q(x)称为反应项系数,b(x,t)为源项.已有的反问题研究中大多处理的是单一的反应项系数或源项辨识问题.例如,当系统源项b(x,t)=0时,Avdonin等人应用边界控制方法研究了基于边界控制、边界观测的反应项系数辨识问题[3];Boumenir等人通过傅里叶分析方法证明了反应项系数可以由边界观测唯一确定[4].当反应项系数q(x)=0时,相应的反问题实际上成为热传导方程的源项反演问题,相关的研究成果也非常丰富,大部分文献中要么假定源项仅依赖于空间变量[5]或时间变量[6],要么假定源项满足时空分离性b(x,t)=h(t)f(x)[7–8],而一般情形时的源项b(x,t)辨识研究结果相对较少[9].此外,一些学者也对系数和源项的联合反演进行了研究,其中辨识所需观测数据主要分为3类:边界观测ω(x0,t)(x0∈∂Ω),固定时刻观测ω(x,T)(T >0),以及时间积分观测ω(x,t)dt,其中µ(t)为权函数.例如,文献[10]分别在固定时刻观测和边界观测情形研究了反应项系数和源项的同时辨识问题,但其要求系统初值取遍状态空间一组标准正交基中的所有元素,这在实际中是不现实的;文献[11]研究了根据3个不同时刻的温度测量同时辨识系统的反应项系数、初值及源项;文献[12]研究了基于两个不同权函数时间积分观测的系数和源项同时反演问题,并给出了数值辨识算法.

从实际工程应用的角度看,很多情况下边界观测更易实现.例如,系统(1)可以用来描述化学反应堆中的温度分布,考虑到控制器和传感器可能无法承受反应堆内部的极端温度和恶劣环境,人们自然希望借助于边界上能够测量到的温度、热流等信息来识别系数及源项,进而对反应堆内部情况进行识别和监测.再比如,在水文地质研究领域,也面临着如何通过抽水井(点控制)、观测井(点测量)中的水位、污染物浓度等信息来识别地下含水层参数或者污染源位置、污染强度等问题.

出于以上考虑,本文主要研究基于边界控制、边界观测的一维反应扩散方程反应项系数和源项的同时反演问题:

其中q(x)表示未知的反应项系数,并且假定它属于如下参数集合:

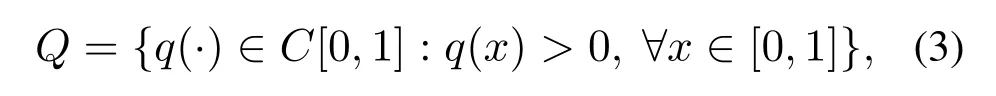
b ∈L2(0,1)表示未知源项,假定它仅依赖于空间变量.u(t)表示Neumann边界控制,yout(t)是边界观测.本文的目标是设计边界控制(0,∞),进而通过有限时间边界观测yout(t),t ∈(0,T]同时识别q(x)和b(x).

本文的创新性主要体现在:1)辨识所需数据仅为边界控制、边界观测,而不需要对系统内部进行分布测量,这比固定时刻观测、时间积分观测在工程中更易实现;2)通过设计边界切换开关控制并估计谱数据,将反应项系数和源项的同时反演问题分解为单一的系数辨识问题和单一的源项反演问题,从而可参考借鉴一些现有辨识算法,极大地简化了多未知量的联合反演问题.特别的,本文中提出的通过设计边界控制进而将多个未知量的联合反演问题分解为单个未知量逐一辨识的方法具有一般性,可将其推广应用于其它一些多未知量同时辨识问题.

2 预备知识

本节主要给出相应正问题的一些预备知识.引入状态空间H=L2(0,1),定义算子A:D(A)(⊂H)→H如下:

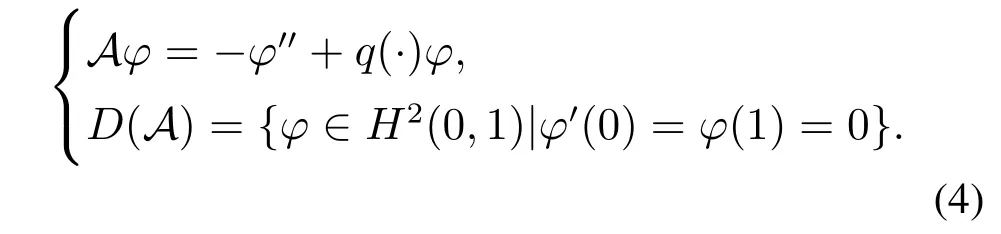
显然,A是正定自伴算子,其本征值λn满足如下渐近表达式[13]:

相应的本征向量φn(x)构成状态空间H的标准正交基,并且

也是t的连续函数.从而,当u(·)∈L∞(0,∞)时边界观测yout(t)在t>0时连续. 证毕.

3 可辨识性

可辨识性是反问题中的一个基本问题,也是辨识算法设计的前提.粗略地讲,如果观测数据中包含充分多的信息能够用来唯一确定待辨识的未知量,则称未知量是可辨识的.为了给出反应项系数和源项的同时可辨识性定义,受文献[16]启发,引入如下参考模型定:

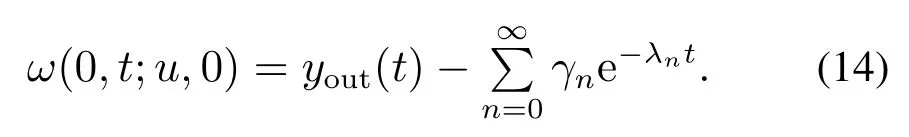
这等价于将系数和源项的同时反演问题转化为单一的系数反演问题,从而原问题得到极大的简化.基于以上分析,设计切换开关控制如下:

其中T2为小于T的任一正数.当t ∈(0,T2)时,观测数据yout(t)=ω(0,t;0,b)可唯一确定{(γn,λn)|γn0}n∈N,进而唯一确定ω(0,t;0,b),t ∈(0,∞);当t ∈[T2,T]时,“输入–输出”映射M:u(t)(0,t;u,0)可唯一确定反应项系数q(x),其中ω(0,t;u,0)由式(14)确定.系数可辨识性得到后,剩下的仅是单一的源项反演问题.这就是整个可辨识性分析的基本思路.

下面,本文将沿着这一思路来证明系数和源项的同时可辨识性.具体的,设T >T2>T1>0是3个任意正数,当t ∈[T1,T2)时,根据式(12)

4 辨识算法

从定理2的可辨识性证明过程可以看出,设计辨识算法的关键在于如何从有限时间观测

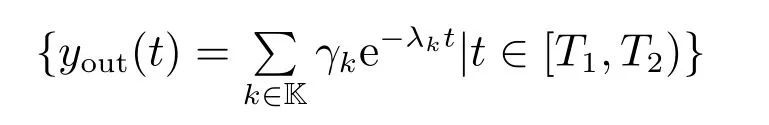
中提取谱数据.一旦得到了谱数据{(γk,λk)}k∈K,就可以将边界观测中由未知源项决定的部分ω(0,t;0,b)从边界观测ω(0,t;u,b)中消掉,从而将原有的系数和源项同时反演问题转化为根据ω(0,t;u,0)辨识系数q(x)这样一个单一的参数辨识问题,辨识出系数q(x)后,剩下的仅是一个单一的源项反演问题,这样就极大地简化了原来的系数、源项同时反演问题.基于上述分析,整个辨识过程由以下3部分构成.

4.1 估计谱数据

令边界控制u(t)=0,t ∈[0,T2),此时,相应的边界观测

4.2 重构反应项系数

当t ∈(T2,T)时,令u(·)∈L∞(T2,T)且几乎处处非零,将边界观测中依赖于未知源项的部分ω(0,t;0,b)从yout(t)中消掉

从而,可将系数与源项的同时反演问题(2)转化为单一的系数反演问题.具体的,构造如下辅助系统:

则原来的系数、源项同时反演问题(2)转化为:根据边界控制u(t),t ∈[T2,T]以及近似“边界观测”{(t),t∈[T2,T]},重构未知系数q(x).对于这样的单一反应项系数辨识问题,现有文献中有多种方法可供借鉴[3,20].

本文将借助于最优扰动正则化算法(见文献[20,第6章])来重构未知反应项系数q(x).设{Pj(x),j=1,2,···,∞}表 示q(x)所在空间的一组基,q(x)满足如下近似展开式:

这样,就完成了一次迭代.继续这一迭代过程直至满足一定精度要求,迭代终止,从而得到最优参数向量这就是通过最优扰动正则化算法重构式(33)中未知系数q(x)的基本过程.

4.3 重构源项

在辨识得到反应项系数后,剩下的相当于单一的源项反演问题.下面根据边界观测yout(t),t ∈[T1,T2)来辨识源项b(x).当t ∈[T1,T2)时,系统(2)可写为

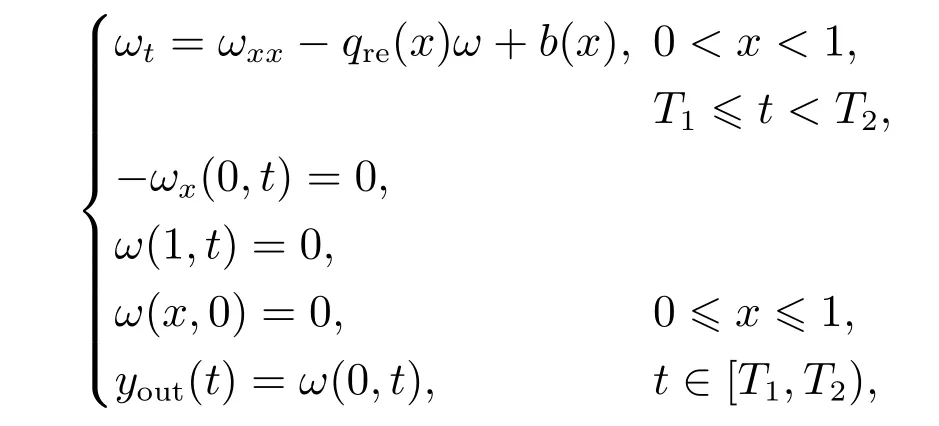
其中qre(x)为反应项系数q(x)的估计值.同样的,对于该源项反演问题,已有文献中也有多种方法来处理[20,22].此处,本文仍采用最优扰动正则化算法通过求解如下优化问题来估计源项:

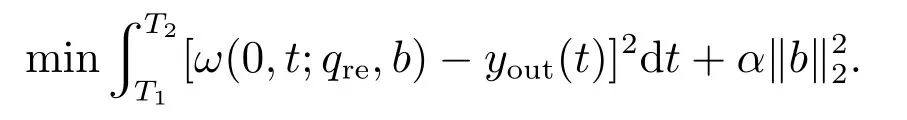
算法的具体过程和第4.2节完全类似,故省略细节.

5 数值仿真

假设系统反应项系数和源项为

选取参数T1=0.1,T2=0.5,T3=1,边界切换开关控制

利用有限差分方法对系统(2)进行数值求解,可得yout(t)=ω(0,t;u,b).下面将{yout(t),0.1 ≤t≤1}作为观测数据,应用第4节中的辨识算法来反演系数q(x)和源项b(x).

本算例中,选取勒让德正交多项式的前五项作为基函数,即

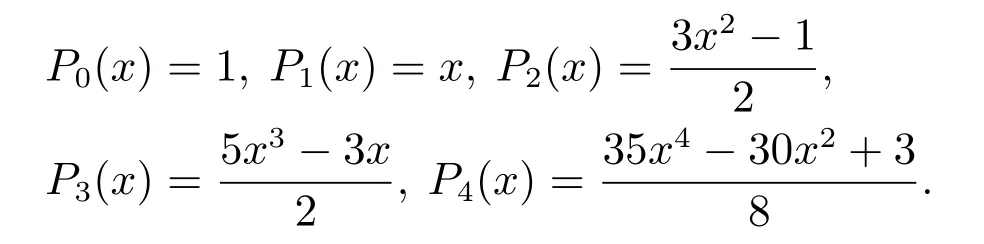
在这样选定的多项式空间Ψ5=span{P0,P1,···,P4}中,反应项系数和源项有如下近似展开式:

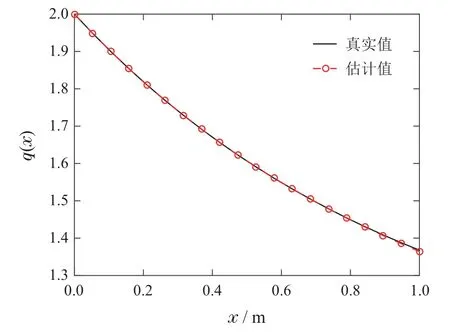
图1 反应项系数q(x)Fig.1 The reaction coefficient q(x)

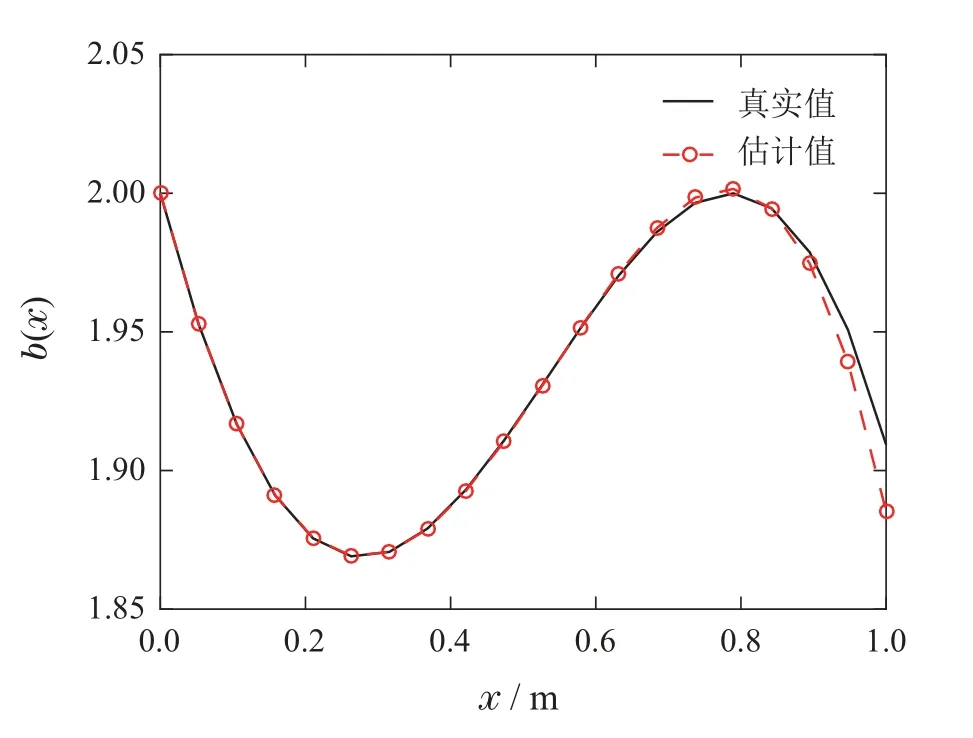
图2 源项b(x)Fig.2 The source term b(x)

可以看出,通过辨识算法重构得到的系数与真实值比较吻合,源项反演结果与真实值之间存在一定误差,但整体仍在可接受范围内,这就验证了辨识算法的有效性.关于源项反演误差,首先,在最优扰动正则化算法中,本文选取勒让德正交多项式作为基函数,用多项式近似非多项式源项,本身就会有一定误差.其次,在源项反演过程中,观测数据和系统模型也都不是完全精确的:一方面,数值模拟中的观测数据yout(t)来自于有限差分得到的数值解,yout(t)本身就带有一定的误差;另一方面,在重构系统源项b(x)时,将已经反演出的qre(x)作为了真实的反应项系数(见第4.3节),这同样会引入一定的误差.