道床-管片界面黏结对隧道变形影响
赵晨,金浩,肖军华
(1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.东南大学 交通学院,江苏 南京 211189)
地铁盾构隧道中的整体式道床在施工时直接浇筑于隧道管片上,两者间界面黏结强度低。当盾构隧道发生较大变形后,管片与道床间产生变形不协调从而导致道床底面与管片间发生剥离,形成脱空,影响轨道对列车的支撑,危及行车安全[1]。目前,针对道床脱空的研究主要集中在脱空的整治措施、检测方法及脱空后道床的受力特征分析。脱空的整治措施主要有注浆加固、道床翻修等[2]。如马伟斌等[3]向道床下填充高强发泡树脂以快速修复道床板脱空病害。道床脱空的检测方法有经验判断法、钻孔取芯法、地质雷达法、钻孔摄像法等[4]。如柳飞等[5]提出利用静力水准仪推算道床剥离量的无损检测方法,并与取芯测量结果对比,证明了静力水准法的可行性。针对道床脱空后隧道结构的受力特征研究。季存建[6]研究了道床下存在脱空时道床在列车荷载作用下的受力及变形,并研究了道床脱空的评价标准。彭华等[7]建立了隧道结构三维有限元模型,分析了在盾构隧道管片沉降作用下道床的变形及损伤情况。然而,整体式道床作为地铁盾构隧道土建结构的组成部分之一,道床与管片共同持荷的工作状态会影响隧道的受力特征与变形规律。因此,有必要研究道床-管片界面黏结对盾构隧道变形的影响规律。本文采用ABAQUS软件,结合南京地区地铁盾构隧道管片结构特点建立包含道床结构的三维盾构隧道有限元模型,利用采用内聚力模型的零厚度黏结单元模拟道床-管片界面以探究界面黏结对盾构隧道变形的影响。
1 盾构隧道有限元模型
1.1 几何模型
盾构隧道外径6.2 m,内径5.5 m,环宽1.2 m。盾构隧道环向分6块,分别为1块封顶块、2块邻接块、3块标准块。其中,封顶块中心角21.5°,邻接块中心角68.0°,标准块圆心角67.5°。盾构隧道采用错缝拼装,以22.5°角交替布置。环缝采用16根M30螺栓,纵缝采用12根M30螺栓。模型中不包含管片的螺栓手孔、嵌缝、倒角、防水密封垫槽等细部构造。钢筋笼包括受力主筋、纵向钢筋与箍筋。建立盾构隧道有限元模型如图1所示。
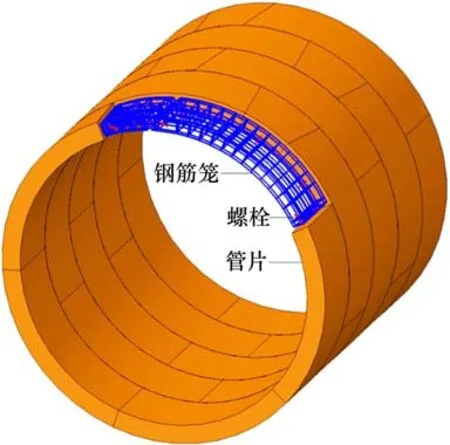
图1 盾构隧道有限元模型Fig.1 FEM model of shield tunnel
1.2 材料参数
管片混凝土采用损伤塑性本构,以模拟盾构隧道管片的开裂和损伤。混凝土损伤塑性本构利用非关联流动法则控制混凝土非弹性体积变形,采用Drucker-Prager塑性势函数G来控制塑形流动的方向,即:

式中:κ为流动势偏移量;σ0为材料破坏时的单轴应力;ψ为高侧压下平面上的剪胀角;pˉ为平均静水压力;ˉ为平均等效有效应力。
管片采用C50混凝土,弹性模量E=34.5 GPa,泊松比μ=0.2,密度2 420 kg/m3,剪胀角ψ=38°,流动势偏移量κ=0.1,双轴与单轴抗压强度比fb0/fc0=1.16,不变量应力比Kc=0.666 7,黏滞系数ν=0.000 01。
采用三折线来表征螺栓、钢筋的弹塑性特征,以模拟钢筋与螺栓在加载中出现的屈服、硬化及软化现象,采用的力学参数[8]如表1所示。
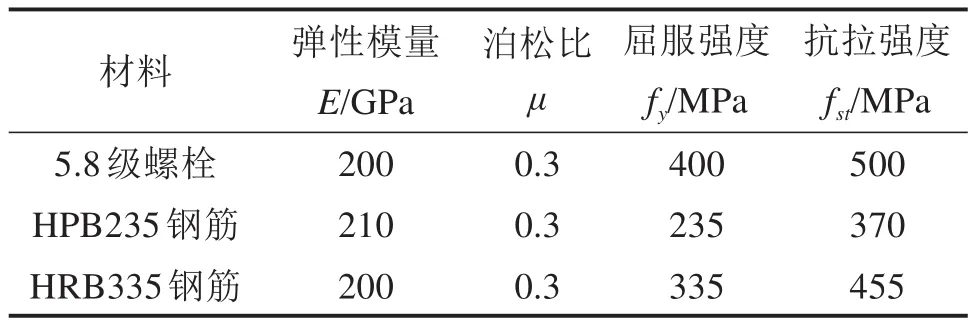
表1 螺栓、钢筋的力学参数Table 1 Mechanical parameters of bolts and reinforcement
1.3 单元类型
管片采用C3D8实体单元进行模拟。螺栓可承受拉力和剪力,采用B31梁单元进行模拟,梁截面与真实螺栓截面一致,钢筋采用T3D2桁架单元进行模拟。螺栓与钢筋通过embedded region约束嵌入管片单元中。
1.4 荷载
本文考虑盾构隧道结构自重及承受的水土荷载。采用荷载−结构模型计算盾构隧道所承受的设计荷载。盾构隧道埋深16 m,土层厚度分别为1.94,16.66和12.20 m;重度分别为18.1,17.5和18.2 kN/m3,侧土压力系数λ分别为0.42,0.70和0.53。荷载-结构模型中P1为隧道顶部承受的垂直水土压力。P5为隧道自重。P2为隧道底部承受的地基反力,其大小等于P1与P5之和。P3和P4分别为作用在隧道顶部和底部的水平侧土压力,由垂直土压力乘以侧压力系数得到。
为模拟盾构隧道的真实变形形态,通过增大P1和P2,为隧道结构施加超载,以获得较大的收敛变形。每1个荷载加载历程代表1倍设计荷载,本文最终荷载加载大小为2倍设计荷载。
1.5 足尺试验验证
为保证盾构隧道有限元模型的正确性,采用同样结构的三环盾构隧道足尺试验进行对比验证[9]。足尺试验装置主要由反力架、持荷梁、千斤顶、底部支撑装置等组成,如图2所示。采用24点集中对称加载来模拟盾构隧道结构实际承受的荷载。

图2 足尺试验装置Fig.2 Test system
足尺试验及有限元计算中隧道水平收敛变形如图3所示。可以看出,有限元计算得到的荷载-变形曲线变化规律与足尺试验结果基本吻合。

图3 水平收敛变形发展Fig.3 Horizontal convergence deformation development
2 道床有限元模型
在错缝拼装盾构隧道有限元模型中加入道床结构,采用整体式道床,高度0.6 m,不考虑道床排水结构等设计细节。道床混凝土强度等级C35,采用CDP本构,弹性模量E=31.5 GPa,泊松比μ=0.2,密度2 390 kg/m3,剪胀角ψ=38°,流动势偏移量κ=0.1,双轴与单轴抗压强度比fb0/fc0=1.16,不变量应力比Kc=0.666 7,黏滞系数ν=0.000 01。道床单元类型为C3D8实体单元。
本文将使用CZM本构的零厚度黏结单元插入到道床与隧道管片的有限元实体之间,用于模拟道床-管片界面复杂的非线性断裂过程,如图4所示。
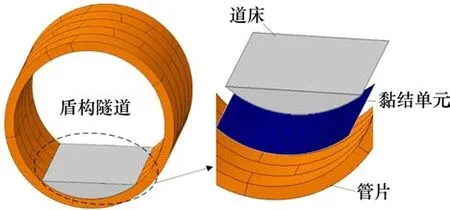
图4 道床数值模型示意图Fig.4 Numerical model of invert-filling
内聚力模型(CZM)最早由DUGDALE[10]和BARENBLATT[11]提出。其通过牵引力−位移曲线来描述内聚力和位移之间的关系。本文采用双线性内聚力本构模型来表征道床−管片界面的开裂,如图5所示。δ0n(δ0s,δ0t),δfn(δfs,δft)代表界面对应方向的起始开裂位移及失效位移;tn0(ts0,tt0)代表界面对应方向的起始损伤应力。

图5 牵引力−位移本构关系Fig.5 Traction-separation constitutive
本文采用黏结单元类型为COH3D8,材料参数[12−13]为:kn0,s,t=104MPa/m,tn0=0.65 MPa,ts0=tt0=4 MPa,GCn=100 J/m2,GCs=GCt=1 000 J/m2。
3 结果分析
3.1 道床脱空过程分析
以中环管片与道床为研究对象,分析超载作用下,道床脱空的发展历程,如图6所示。道床脱空最先发生于道床的边界,随着水平收敛变形的增大,道床脱空的边界基本以平行的方式向道床中央发展。道床脱空的发展过程可用道床-管片界面层边缘与道床边缘的夹角θ表征。未发生脱空时,脱空角度θ=0°;在2倍荷载作用下,脱空角度达到最大值为28.5°。
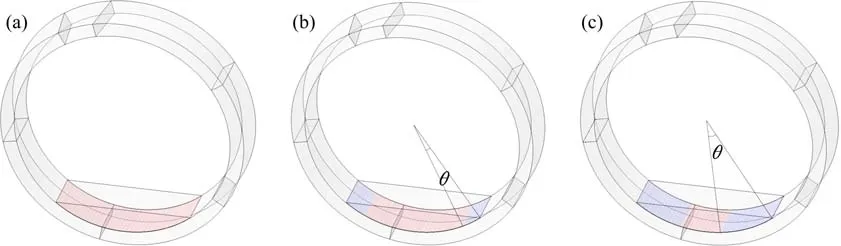
图6 道床脱空示意图Fig.6 Disengaging diagram of invert-filling
两模型中环的水平收敛变形与脱空角度如图7所示。道床结构对盾构隧道管片的黏结牵拉会减小隧道收敛变形的大小。根据不同阶段道床脱空的发展,可将加载历程分为3个阶段。阶段Ⅰ:当荷载小于1.16倍设计荷载时,不发生道床脱空;阶段Ⅱ:1.16~1.40倍设计荷载阶段。开始道床脱空,且脱空的发展速度最快。道床脱空角度从0°发展至21.9°;阶段Ⅲ:荷载大于1.40倍设计荷载阶段。道床脱空速率放缓,此时脱空已基本结束,至达到2倍荷载时,道床脱空角度达到28.5°。

图7 水平收敛变形、脱空角度与荷载关系曲线Fig.7 Horizontal convergence deformation, disengaging angle and load relationship
包含道床模型的隧道收敛变形也可根据以上分界点分为3个阶段。当不发生道床脱空时,水平收敛变形线性增长;当脱空快速发展时,水平收敛变形也加速发展,直至脱空放缓阶段,隧道变形也进入了减速发展的拐点。由于产生脱空,道床−管片界面的面积减少,道床对管片的约束作用减弱,因此收敛变形有以上变化趋势。
3.2 界面黏结对管片内力的影响
从道床边缘向道床中心每5°共9个截面对管片进行剖分。其中道床边缘为0°截面,道床中心(拱底)为40°截面。提取加载历程下各截面管片的轴力和弯矩并计算偏心距,其中轴力方向与截面垂直,以管片受压为正;弯矩方向以管片外侧受压、内侧受拉为正。
由图8可知在加载历程中,两模型中道床下管片轴力从道床边缘(0°截面)至拱底(40°截面)依次增大,且各截面间轴力大小关系不变。由图8(b)可得无道床模型中各截面轴力随荷载线性增加。由图8(a)可知,道床脱空会影响管片轴力的增长规律。当荷载达到1.16倍设计荷载时,脱空边缘所在截面处管片轴力下降,当脱空边缘“越过”该截面后,轴力继续增加。
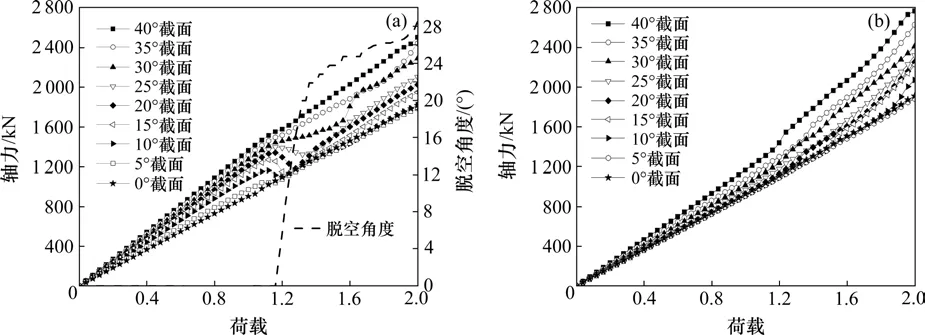
图8 2种模型管片轴力对比Fig.8 Comparison of axial forces of two models
如图9所示,发生脱空前,管片弯矩从道床边缘至拱底依次增大;开始脱空后,0°~10°截面管片弯矩先减小后增加,其余截面管片弯矩迅速增加;至脱空基本结束后,所有截面管片弯矩随荷载增长而增加,且弯矩大小排序发生颠倒。此时弯矩排序与图9(b)中各截面管片弯矩的大小关系相同。这是因为:脱空前,道床与管片间黏结完整。荷载增加时,道床与管片共同持力,道床限制了管片的“横鸭蛋”变形,道床下管片产生向外侧的径向位移较小,因此具有更大弯矩。
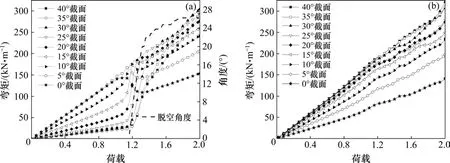
图9 2种模型管片弯矩对比图Fig.9 Comparison of bending moments of two models
图10中对两模型偏心距的对比也说明了道床所起到的限制盾构隧道变形作用。道床脱空前道床边缘截面具有更大的偏心距,发生脱空后,0°~5°截面偏心距减小,其余截面偏心距增加。这是因为:开始脱空后,边缘处道床对管片变形的限制作用减小,道床下的管片有向外变形的趋势,增加了径向位移。但由于脱空时道床−管片界面荷载的释放且随着隧道收敛变形的增加,脱空向拱底方向发展,未脱空区域的拉应力增加,由此造成弯矩以及偏心距的增加,直至脱空基本结束后,道床下各截面管片与偏心距的大小排序规律与无道床模型中规律相同。
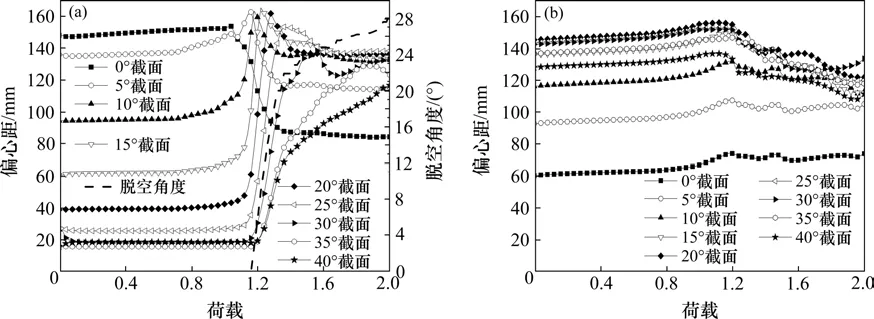
图10 2种模型管片偏心距对比Fig.10 Comparison of eccentricity of two models
3.3 界面黏结对管片损伤的影响
图11为2类模型中环管片受拉损伤云图对比。当混凝土拉应变达到其2倍峰值拉应变时,混凝土会产生可见裂缝[14]。图中仅显示可见裂缝的混凝土区域。由图11(a)可得,在含道床的模型中,当荷载达到1.14倍设计荷载时,道床边缘下部管片首先产生受拉裂缝。随着收敛变形的增加,损伤区域向拱底方向扩展,最终当荷载达到2倍荷载时,脱空边缘处管片产生较大损伤。这是因为:由图10(a)可知,发生道床脱空前,道床边缘处管片具有更大的偏心距,此时的管片截面内会出现较大拉应力。而混凝土的抗拉强度明显低于其抗压强度,受拉侧的应力极容易超过抗拉强度而导致混凝土裂缝出现[15]。由图11(b)可得,在不含道床模型中,损伤首先发生在拱底,而后随着荷载增加,损伤区域向两侧扩展。
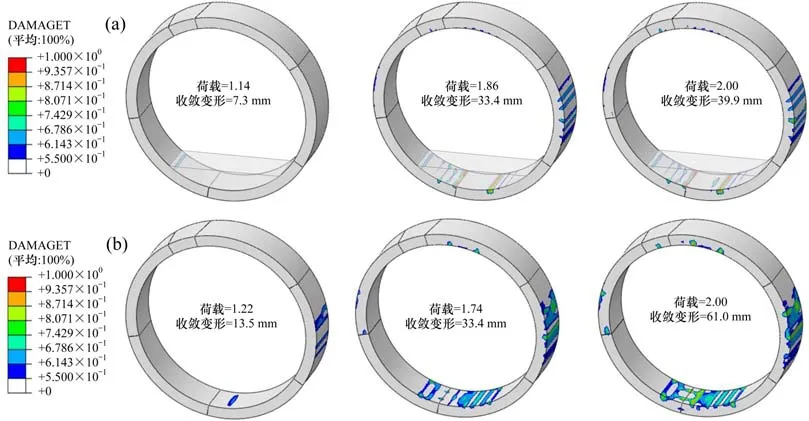
图11 2种模型管片损伤对比Fig.11 Comparison of segment damage of two models
对比相同水平收敛变形下(33.4 mm)两模型的管片损伤情况,含道床模型的损伤区域更小,但损伤程度较深,道床-管片界面的黏结可能会引起道床下管片产生贯通裂缝。对比相同荷载下(2倍设计荷载)的损伤情况,由于道床对管片的牵拉作用,含道床模型的隧道具有更小的水平收敛变形,因此其道床下管片具有更小的损伤区域。
4 结论
1) 道床结构对盾构隧道管片有牵拉作用,会减小隧道水平收敛变形的大小。道床脱空最先发生于道床的边缘,随着水平收敛变形的增大,道床脱空的边界基本以平行的方式向拱底发展。随着道床脱空的发展,道床对管片的约束效果减弱,隧道水平收敛变形快速增加;至脱空基本结束后,收敛变形增速放缓。
2) 道床对管片的黏结会影响道床下管片的受力特点。在持荷过程中,道床−管片界面不影响管片各截面内力大小的顺序。但截面弯矩及偏心距大小排序在脱空前后发生颠倒,其会影响管片损伤的发展规律。
3) 道床−管片黏结界面的存在会影响隧道拱底管片损伤区域及损伤程度。由于道床黏结拉伸管片,在隧道变形过程中,道床边缘处管片首先产生受拉裂缝。相同收敛变形下,由于道床-管片界面的存在,管片损伤区域小,但损伤程度较深,拱底产生贯通裂缝的风险更高。

