需求导向的高铁列车差异化定价与票额分配综合优化

苏焕银，徐光明，曾琼芳，彭舒婷，贾旭东

(1.五邑大学 轨道交通学院，广东 江门 529020；2.中南大学 交通运输工程学院，湖南 长沙 410075；3.湖南工商大学 旅游管理学院，湖南 长沙 410205)

近些年，中国高速铁路的建设和发展取得了巨大成绩，对中国经济发展起到重要支撑作用。2016年1月1日起，中国发改委调整了对高速铁路列车票价的管制。自政策发布以来，铁路公司相继在部分线路列车上进行了票价浮动的尝试。体现出中国高速铁路列车的客票定价机制市场化运作，考虑不同旅客出行需求特征以及列车服务质量区别，实行优质优价、灵活浮动的票价机制。因此，本文从网络规模着手，结合我国铁路旅客出行需求的特征，研究高速铁路多列车差异化定价和票额分配综合优化方法，对于提高铁路运输企业的经济收益具有重要意义。高速铁路列车票价的优化和票额分配属于收益管理问题，近些年受到越来越多的学者关注[1−2]。一些学者专门研究了高速铁路列车的票价问题。ZHANG等[3]研究了高速铁路列车团体票的定价问题，但只考虑一趟车的始发终到站之间的旅客需求。ZHENG等[4]针对中国高速铁路列车的票价优化问题进行了研究，设计了单趟列车在预售期内的票价优化方法，将优化模型设计为凸规划，采用拉格朗日乘子和KKT条件对模型进行求解。张旭等[5]依据列车席位存量的变化动态设计票价，考虑旅客在民航与高铁之间的选择行为，但是只针对单个OD对和单个列车车次的不同等级席位研究。景云等[6]考虑了旅客在多种高铁车型以及航空运输之间的选择行为，研究高速铁路列车在预售期内的动态定价问题，但是只考虑了一个OD对。赵鹏等[7]针对单个出行OD对旅客需求研究高速铁路列车差别定价方法。QIN等[8]基于前景理论研究了高速铁路多趟列车的差别定价方法，采用模拟退火算法进行求解。鉴于实际问题的复杂性和求解难度，较少学者研究多列车的票价优化问题，多数学者将研究范围限定在一趟列车或一个OD对等较小的规模上，简化了研究问题，通常采用离散选择模型分析旅客的选择行为。也有些学者研究了固定票价方案下的列车票额分配问题。WANG等[9]研究了铁路旅客运输中多列车的席位分配问题，根据是否在预售期内分时段分配票额，将问题分为单阶段和多阶段决策，设计了2个随机规划模型。假设旅客出行需求在预售期内随机到达，符合泊松过程，并采用多项Logit模型描述旅客的路径选择行为，综合考虑旅途时间、票价和席位舒适度。JIANG等[10]研究了中国高速铁路收益管理问题，结合短期动态客流需求预测方法，动态调整预售期内多趟列车的席位分配方案，提高整体列车网络收益。YAN等[11]研究了多列车的席位分配和列车编组问题的综合优化方法，考虑了随机需求以及旅客的选择行为，分析了需求强度、票价等级以及需求弹性的影响。高速铁路列车票价的优化和票额分配虽然是收益管理中的2个环节，但并不是相互独立的。票价的调整影响旅客的出行选择，进而影响到各个出行OD对的需求量，而旅客的出行需求是否得到满足又受到票额分配的牵制。因此，这2个环节相互影响，一些学者对二者进行了综合优化研究。QIN等[12-14]研究了预售期内高速铁路多列车票价浮动和席位分配的综合优化方法，采用人工蜂群算法、两阶段算法以及基于超分方程的分步算法进行求解。HU等[15]研究了高速铁路多列车动态定价和席位分配综合优化问题，采用拟牛顿方法进行求解。YAN等[16]研究了不同运行交路的多列车票价和席位分配综合优化方法，采用粒子群优化算法进行求解。周文梁等[17]基于列车服务水平的多项指标将列车聚类分级，构建多类列车的差异化票价和票额协同优化方法，采用模拟退火算法进行求解。但这些研究对旅客出行需求特征的分析不够深入，对旅客出发时段的选择偏好缺少研究。鉴于此，本文依据历史售票数据研究旅客出行需求的出发时段偏好特征，采用多项Logit模型分析不同出发时段偏好的旅客需求在多列车之间的选择行为。以客票收入最大化为目标构建多列车差异化定价和票额分配的协同综合优化模型，设计改进的直接搜索模拟退火算法进行求解。

1 旅客时变需求

旅客出行需求是设计票价和票额分配的基础。依据历史售票数据对旅客需求从出发时段和出发星期的维度上进行统计分析，获得每个OD对在一周内每天的每个小时内的平均需求分布情况，如图1所示。根据图1可知：1) 旅客需求随着出发时段的变化具有明显高峰与低谷，具有一定的波动规律性；2) 一周内每天的旅客需求体现的波动特征具有较大的相似性；3) 不同OD对的出行需求体现出来的波动特征具有明显的不同。

图1 旅客的出行需求分布Fig.1 Passenger demand distribution

上述特征称为旅客需求的时变特征，对应的旅客需求称为时变需求。根据历史售票数据采用统计回归方法获取旅客需求的出发时段概率分布，描述旅客时变需求。将一天的运营时间划分成若干时段，时段总数记为K，时段变量记为k，那么k=t0,t0+1,…,t0+K-1，其中t0表示初始时段。将旅客出行OD对记为(r,s)，r为上车站，s为下车站。OD对(r,s)一天内的旅客需求记为qrs，旅客需求位于第k个出发时段的概率记为frsk，旅客在出发时段k内的需求记为qkrs，那么

2 旅客出行选择行为分析

采用多项Logit模型分析旅客时变需求如何在差别定价的多趟列车中选择，以此确定每趟列车的旅客需求，进而评估票价和票额分配方案。所有车站组成的集合记为SN，所有OD对组成的集合记为RS。所有列车组成的集合记为W={j}。对于列车j∊W，记h(j)为列车j的停站数，STj=(vj1,vj2,…,vjh(j))为列车j的沿途停站序集(vjx∊SN)。列车j在停站vjx至停站vjy的运行区段称为列车区段，记为(vjx,vjy)。列车j的运行区段组成集合，记为Legj。对于x≤x'且y'≤y，称运行区段(vjx,vjy)覆盖运行区段(vjx',vjy')，记为(vjx',vjy')⊆(vjx,vjy)。

将在OD对(r,s)停靠的列车组成的集合记为Wrs。列车j在OD对(r,s)之间的旅行时间记为trs(j)，票价记为crs(j)。旅客的出行成本综合考虑出发时间偏差、旅途时间和票价，根据多项Logit模型原理，OD对(r,s)的旅客时变需求qkrs选择列车j的概率为

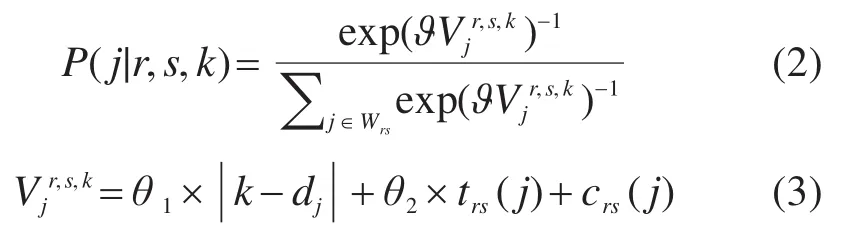
其中，Vr,s,k j表示旅客的出行成本；dj表示列车j的出发时段，选择列车j出发的旅客的实际出发时段即为dj；k为旅客的期望出发时段，那么|k-dj|表示旅客的出发时间偏差绝对值；θ1和θ2为时间价值系数；ϑ为换算系数。

那么，对于OD对(r,s)，期望出发时段为k的旅客选择第j趟列车的需求为qkrsP(j|r,s,k)。第j趟列车在运行区段(r,s)上的总旅客需求记为Djrs，表示如下：

3 高速铁路多列车差异化定价和票额分配的协同综合优化模型设计

在综合优化模型的设计中，本文采用指数函数来描述列车票价对旅客出行需求总量的影响，即弹性需求，如式（5）所示。

其中，表示OD对(r,s)的平均列车票价；当OD对(r,s)的平均列车票价为时，旅客出行需求为，依据历史售票数据获取；参数ϕ取值越大，表示需求的价格弹性越大。

列车j在运行区段(r,s)上的票额记为mrs(j)，每个列车运行区段上能够接收的旅客需求受到票额的限制。因此，列车j在运行区段(r,s)上实际接收的旅客需求表示为min{Djrs,mrs(j)}。那么，以高速铁路多列车的客票收入最大化为目标，以票价crs(j)和票额mrs(j)，(r,s)∊Legj，j∊W，为决策变量的综合优化模型可表示如下：

其中，cminrs和cmaxrs分别表示列车在运行区段(r,s)上的票价允许取值的下限和上限，约束条件(8)表示每个列车运行区段上叠加的票额不超过列车运输能力。

上述综合优化模型体现了高速铁路运营决策者和旅客之间的相互作用机理。首先，高速铁路运营决策者在约束范围内制定相应的票价方案；然后，在给定的票价方案下，旅客依据效用最大理论进行出行选择，决定了每个列车运行区段上的旅客需求；然后，依据每个列车运行区段的旅客需求以及相应的票价，运营决策者在运输能力约束下制定票额分配方案，完成对整体方案的评估。这是一个相互牵制、相互影响的过程。

4 启发式优化算法设计

本文综合优化模型的决策变量较多，问题规模较大。模拟退火算法[18]具有全局收敛性，被广泛应用于工程实践。为了提高算法在求解高维度优化问题时的收敛稳定性和收敛效率，对新解生成方法以及算法结构进行了改进，设计了改进的直接搜索模拟退火(MDSA)算法。分两阶段构造优化模型的解，首先在票价约束范围内构造票价方案，并依据式(1)～(5)计算每个列车运行区段上的旅客需求；然后计算给定票价方案下的最优票额分配方案。

记票价决策变量的个数为cn，令C，CL和CU分别为决策变量票价组成的向量及其下限和上限，均为cn维列向量。那么，

满足式(9)的票价解向量构成票价方案C的搜索空间，记为S。在搜索空间S中随机生成N=7(cn+1)个票价方案[18]，计算每个票价方案C下的最优票额分配方案，记为M*(C)={m*rs(j)|(r,s)∊Legj,j∊W}，及目标函数Z，构成初始解集合，记为A。在解集合A中，对应目标函数值最大的票价方案记为CBest，对应目标函数值最小的票价方案记为CWorst，相应的目标函数记为Zmax和Zmin。

4.1 票价方案的生成方法

1) 变尺度柯西分布随机生成票价方案

在搜索空间S内按变尺度柯西分布产生票价方案C，该方法记为GNS1。计算公式如下：

式中：符号“◦”表示Hadamard乘积；y是由变尺度柯西分布随机产生的cn维单位列向量；abs(*)为取绝对值函数；w为(0,1)内按均匀分布产生的随机数。该方法可实现优化初期的大范围搜索和优化后期的小范围精细搜索。

2) 组合随机生成票价方案

首先从解集合中随机选取RN个票价方案，记为{cn1,cn2,…,cnRN}，将RN个解与票价方案CBest进行随机的组合生成新票价方案C，其每个分量ci由式(11)确定。该方法记为GNS2。

其中，wi为[0,1]内按均匀分布产生的随机数。该方法可以提高CBest的搜索效率，提高算法的收敛稳定性。

3) 自适应方法随机生成票价方案

自适应方法中的票价方案C是在搜索空间S中票价方案CBest邻域内按正态分布随机扰动产生的，该方法记为GNS3，可避免搜索过早陷入局部极值。

式中：符号“◦”表示Hadamard乘积；b为搜索半

径调节系数；I为自适应因子；y是按标准正态分布随机得到的cn维单位列向量。若票价方案C超出搜索空间S，则由式(13)修正C中的各个分量：

对于新构造的票价方案，采用上述的式(1)～(5)计算每趟列车运行区段的旅客需求Djrs，(r,s)∊Legj,j∊W。

4.2 给定票价方案下的最优票额分配方案生成方法

在给定票价方案C={crs(j)|(r,s)∊Legj,j∊W}和每个列车运行区段上的旅客需求Djrs，(r,s)∊Legj,j∊W的前提下，综合优化模型转化为票额分配优化模型，如下：

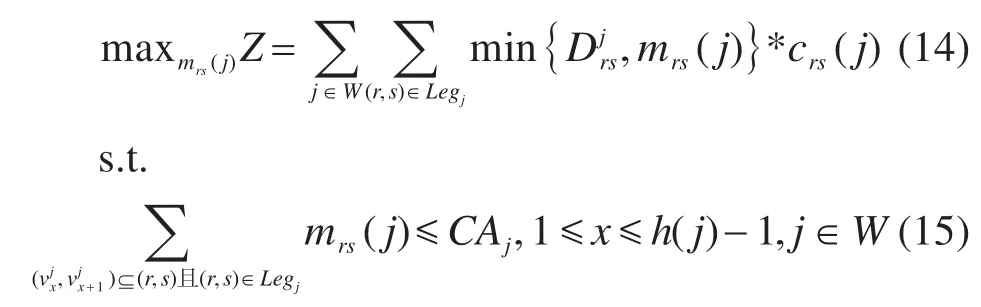
对于满足式(15)的任意票额分配方案{mrs(j)|(r,s)∊Legj,j∊W}， 假 若 存 在 某 个mrs(j)>，那么min{Djrs,mrs(j)}=Djrs，表示该列车运行区段上分配的票额超过了旅客的需求，部分票额(mrs(j)-Djrs)被闲置。闲置的票额并没有产生实际的票额收入，如果将这部分票额收回，即调整mrs(j)， 令mrs(j)=Djrs， 那 么min{Djrs,mrs(j)}=Djrs。因此，调整后的票额分配方案的优化目标可保持不变(对应的客票收入不变)，且式(15)仍然满足(票额分配变小了)，仅仅是收回了闲置的票额，使得调整后的票额刚好匹配旅客的需求。

因此，不失一般性，在保持优化目标不变的前提下，可在上述优化模型中添加约束条件mrs(j)≤Djrs,(r,s)∊Legj,j∊W， 那 么 min{Djrs,mrs(j)}=mrs(j),(r,s)∊Legj,j∊W。上述票额分配优化模型可调整如下：

s.t.

式(15)

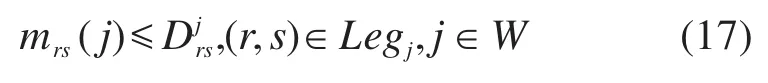
在保持优化效果不变(最优客票收入不变)的前提下，调整后的票额分配优化模型的目标函数简化了，方便采用Cplex优化器求解，计算给定票价方案C下的最优票额分配方案M*(C)及目标函数Z(C,M*(C))。

4.3 MDSA算法设计

在MDSA算法中，新解(C,M*(C))被接受的概率Pacc按照式(18)计算：

其中，Ta为第a次降温得到的温度。若连续几次降温(以Δa标记，Δa<τ，τ为给定参数)中Zmax无明显改变(即ΔZmax=Za+1max-Zamax≤δ，δ为给定的正实数)作为算法陷入局部极值的判据。马氏链长度La按照式(19)计算，是MDSA算法内层循环次数的上限。

MDSA算法的具体步骤如下所示。

1) 构造初始解集合A，确定CBest，CWorst，Zmax和Zmin。初始化参数，确定初始温度T0，降温迭代次数a=0。计算马氏链长度La，令Δa=0。

2) 令i=0。

3) 令i=i+1。若Δa<τ，则按一定的概率采用方法GNS1和GNS2生成新票价方案C；否则采用方法GNS3生成新票价方案C。

4)计算票价方案C下每个列车运行区段上的旅客需求。采用Cplex优化器计算最优票额分配方案M*(C)以及目标函数Z(C,M*(C))。

5)计算被接受概率Pacc，在[0,1]内产生随机数Pran。若Pran≤Pacc，则从集合A中删除最差解并添加新解(C,M*(C))到集合A中。

6) 若新解C,M*(C)是集合A中的最优解或者i等于La，则更新CBest，CWorst，Zmax，Zmin和 Δa；否则更新CWorst和Zmin，转步骤3。

7) 若Ta≤ε1且Zmax-Zmin≤ε2，则算法结束；否则令a=a+1，更新马氏链长度La和温度Ta，转步骤2。

5 数值实验

5.1 实验设置

选取武广高速铁路51趟列车进行实验，涉及11个OD对和8个车站(武汉、岳阳东、长沙南、衡阳东、郴州西、韶关、广州南和深圳北，依次编号0至7)。以小时为间隔，将一天的运营时间[6:00,23:00]划分为17个时段。根据历史售票数据确定每个OD对(r,s)的固定票价及旅客需求q0rs，如表1所示。固定票价下客票收入为Z0=10 721 194。列车在每个运行区段的票价下限和上限是在固定票价的基础上下浮30%和上浮30%。

表1 各 OD对的固定票价(上限和下限)和需求Table 1 Fixed prices and demands of OD pairs(the upper limits and the lower limits)

优化算法中解的维度cn=296，解集合的大小N=2 079，在算法运算初期，马氏链长度La=5 920。收敛精度ε1=0.05，ε2=0.05。时间价值系数θ1=0.8元/min，θ2=1元/min。在算法运行前期(a≤50)，以较大概率采用GNS1方法生成新票价方案，提高搜索空间S的覆盖范围。在算法运行后期(a>50)，以较大概率采用GNS2方法生成新票价方案，提高算法收敛效率。当算法陷入局部极值时采用GNS3方法生成新票价方案，跳出局部极值。

5.2 优化结果及分析

采用C#编程，针对9个不同弹性需求系数ϕ进行优化计算分析，优化解的客票收入记为Z*，Z*相比Z0的变化比例记为ΔZ，计算结果如表2所示。根据表2可知优化解的客票收入明显提高，受弹性需求系数ϕ影响较大，提高了9%～27%，旅客出行需求满足率达到97%以上。当ϕ=1时，客票收入提高最小；当旅客出行需求缺乏弹性(ϕ较小)或者富有弹性(ϕ较大)时，客票收入提高幅度较大。在算法降温200次时，优化目标已经实现了97%以上，降温总次数较多是因为算法收敛精度设置较高所致。不同弹性需求系数下优化解的迭代收敛情况如图2所示。根据图2可知，算法收敛效果较好，算法在迭代到50次以后收敛效率明显提高，说明采用GNS2方法生成票价方案可以显著提高算法收敛效率。

表2 优化结果Table 2 Optimal results

图2 优化解的收敛图Fig.2 Convergence of the optimal solutions

选取弹性需求系数为0.6和1.4 2种情况进行分析。表3展示了优化解的部分票价方案，表4展示了优化解部分列车的票额分配方案以及旅客需求。根据表3可知，不同出发时段的列车票价具有差异性。当ϕ=0.6时，列车的票价多数靠近上限，说明在旅客出行需求缺乏弹性的情况下，提高列车票价可以提高客票收入。当ϕ=1.4时，列车的票价多数低于固定票价，说明在旅客出行需求富有弹性的情况下，降低列车票价可以提高客票收入。根据表4可知(标注下划线部分为票额分配与需求不相等的情况，未标注的为完全匹配的情况)，大部分列车区段上的票额分配和旅客出行需求刚好相等，在出现偏差的列车运行区段上，多数偏差不超过1，极少数偏差大于1的情况也是出现在短途运行区段上，如运行区段2-3和5-6。因此，列车在各个运行区段上的票额分配方案与相应的旅客需求高度匹配，说明票额分配方案的合理性以及优化方案的需求导向性。

表3 优化解的部分票价方案(ϕ=0.6/ϕ=1.4)Table 3 Part train prices of the optimal solutions (ϕ =0.6/ϕ =1.4)

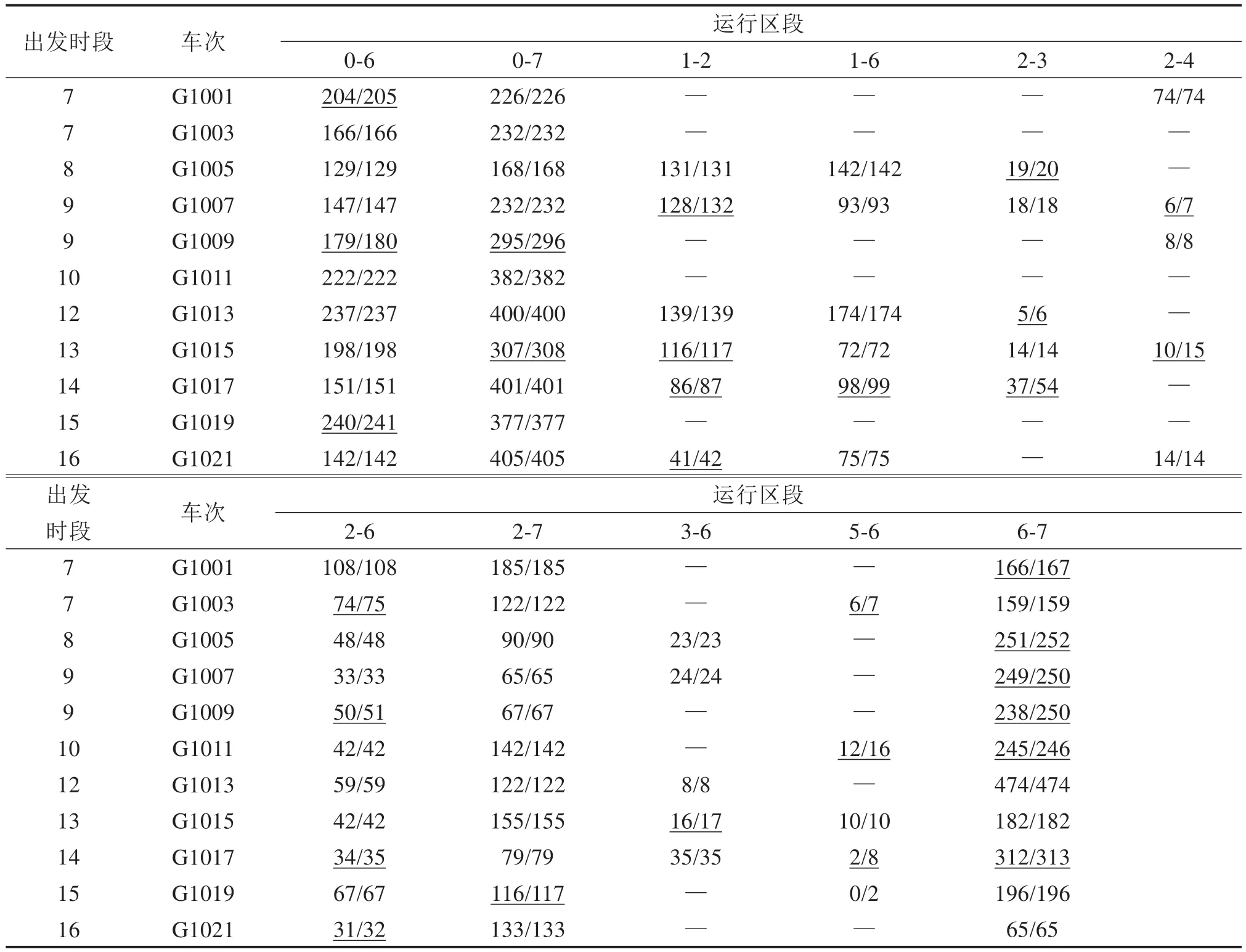
表4 优化解的部分列车票额分配方案/旅客需求(ϕ=1.4)Table 4 Seat allocations of part trains for the optimal solution/passenger demand (ϕ=1.4)

6 结论

1) 综合考虑旅客出发时间偏差、旅途时间和票价支出3项因素设计了多项Logit模型，分析旅客在差异化定价的多列车之间的选择行为。以客票收入最大化为目标构建高速铁路多列车差异化定价和票额分配的协同综合优化模型。

2) 将解的生成分为2个阶段，第1阶段采用变尺度柯西分布随机生成方法、组合随机生成方法和自适应随机生成方法构造票价方案，第2阶段采用Cplex优化器求解给定票价方案下的最优票额分配方案。设计了基于两阶段的改进直接搜索模拟退火算法对优化模型进行求解。

3) 选取武广高速铁路的51趟列车进行实验分析。计算结果表明算法整体收敛效果较好，优化解的客票收入受弹性需求系数的影响较大，提高了9%～27%。不同出发时段的列车票价具有差异性，列车在各个运行区段上的票额分配方案与相应的旅客出行需求高度匹配，说明优化方案的需求导向性。