考虑服务水平的高速铁路通过能力利用研究

邹信诚 ，李海鹰，廖正文，孟令云

(1.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044；2.北京交通大学 交通运输学院，北京 100044)

铁路客运部门在制订旅客列车开行方案时，一方面需要考虑开行一定数量、一定结构的旅客列车，以尽可能满足旅客不同层次的出行需求，另一方面还需要考虑开行方案编制结果的可行性，即制订的列车开行方案是否满足线路的通过能力约束。铁路线路的通过能力影响因素很多，特别是对高速铁路而言，其通过能力受到列车速差、停站等取决于列车开行方案的因素影响很大，因此编制列车开行方案需要反复进行“开行方案制订(或调整)——能力约束校验”这一循环迭代的过程，以保证编制得到的开行方案既满足旅客需求，又满足能力约束。在此过程中，针对特定开行方案的能力计算是一个非常重要的环节。目前，采用扣除系数法等分析计算方法难以准确计算高速铁路的通过能力，而采用仿真法、优化图解法等方法耗时较长，影响计划循环迭代编制的效率。因此，如何快速有效地权衡特定列车开行方案满足旅客出行需求和通过能力利用的关系，加速以上循环迭代过程，成为了旅客运输计划编制人员亟需解决的问题。在现有的铁路能力研究中，学者们往往从供给的角度研究能力的利用，即从固定设备、活动设备、行车组织等方面出发。如分析计算法：赵东等[1]将列车占用总时间与列车运行图有效开行时间带的比值计算通过能力利用率；张守帅等[2]分析证明了原有的扣除系数法不适用于高速铁路能力计算；武旭等[3]针对高速铁路无越行区段，提出基于平均最小间隔时间的区段通过能力的计算方法；JENSEN等[4]通过求解同一类型列车平均等待时间最小的最大列车集合得到通过能力值。如优化图解法：ZHANG等[5]利用运行图的最小周期来表征通过能力利用情况；王宇强等[6]通过优化高速铁路列车的时刻表和停站方案实现能力利用优化；LIAO等[7]考虑了活动设备数量，使用时空网络的建模方式铺画满表运行图来计算运输能力；李海鹰等[8]采用基于压力测试法和滚动分段求解法铺画满表运行图的方式计算既有线释放能力。如仿真法：LJUBAJ等[9]使用仿真软件Open‐track来模拟铁路运输的微观过程，以优化车站和线路的能力利用；KIANINEJADOSHAH等[10]使用仿真软件Opentrack分析了通过提速提高铁路能力的可能性。但这些研究都是以能力的最大利用为目标，未研究出行需求与能力之间的规律。出行需求可以分为位移需求和服务水平需求，当旅客位移的需求得到满足后，服务水平成为了旅客最为关心的问题。目前，分析不同服务水平下通过能力利用的研究较少。例如，安婷[11]定性分析了服务水平对通过能力的影响；鞠浩然等[12]将服务水平分为5个等级，通过调整运行图冗余时间计算分析服务水平和通过能力的关系。这些研究将服务水平归结为取决于运行图指标相关的因素，未考虑具体的客流分布差异，难以精准地表征旅客的出行体验。陈柯冰[13]分析了高铁列车开行结构对区间通过能力的影响；夏昭辉[14]定量分析了速差系数、平均停站距离等因素对扣除系数的影响；郑金子等[15]基于扣除系数法分析了不同运输组织模式对京沪高铁通过能力的影响。结合开行方案编制人员的经验可知，线路的通过能力和开行方案的一些特征(如列车的停站数量、运行线的异质度等)存在一定的相关关系，而这些特征对旅客出行的影响体现在服务水平上，因而可以发掘并利用服务水平与通过能力之间的相关关系规律，用于评估特定开行方案的能力利用情况。为了解决计划编制人员权衡服务水平和线路通过能力利用的问题，本文提出考虑开行方案服务水平的线路通过能力利用评估方法。首先选取用于衡量列车开行方案服务水平的指标，然后，调节列车开行方案优化模型的参数得到一定客流需求下对应于不同服务水平的列车开行方案；再以这些开行方案为输入铺画满表列车运行图，以满表列车运行图中的列车数量表示采用不同开行方案作为行车组织方法的线路通过能力，同时计算这些开行方案的服务水平指标，从而分析得出在特定客流需求条件下的服务水平与通过能力利用的定量关系，以在制订开行方案时权衡服务水平和通过能力利用，优化铁路列车开行方案的编制流程，提升开行方案编制质量。

1 基于列车开行方案的服务水平指标

铁路旅客运输的服务水平可以从便捷性、舒适性、快捷性、安全性和准时性等维度来衡量，其中便捷性、舒适性和快捷性受列车开行方案中的列车数量和停站的影响很大，而安全性和准时性受设备可靠性和调度指挥水平影响较大，而受开行方案编制的影响较小。本文将服务水平的范围界定为取决于开行方案的服务水平指标，这些指标的差异主要体现在列车开行数量和停站方案上。为此，从便捷性、舒适性和快捷性出发，提出基于列车开行方案的服务水平指标。

结合高速铁路旅客运输的现状和计划编制阶段的特点，本文提出平均旅客服务频率、平均额外停站次数和客座利用率3个基于列车开行方案的服务水平指标，在列车开行方案给定的情况下，可以使用以下公式计算各服务水平指标的值。

1.1 平均旅客服务频率

平均旅客服务频率指的是平均每位旅客在不换乘的条件下，一天内可以选乘的列车数量，可由式(1)计算得到。

式中：(s1,s2)为出发站为客运站s1，到达站为客运站s2的OD对；Q为OD对集合；q(s1,s2)为OD对(s1,s2)的客流量，单位为人；f为列车；F为开行方案中的所有列车集合；θ(s1,s2)f表示列车覆盖OD的参数，若列车f在客运站s1和客运站s2均停站，该参数取1，反之取0。

在开行方案中，开行的列车数量越多，或列车的停站次数越多，某旅客可以选乘的列车数量往往可能会越多，平均旅客服务频率就越大。该指标反映了铁路旅客运输的便捷性，越大意味着可供旅客选择的列车数越多，便捷性就越好。

1.2 平均旅客额外停站次数

对于旅客而言，平均旅客额外停站次数指的是平均每位旅客在旅行途中经历的额外停站，即从旅客上车到旅客下车期间，其乘坐的列车在沿途各站的停站次数，可由式(2)计算得到。

式中：q(s1,s2)f表示列车f运送从客运站s1到客运站s2的客流量，人；ψ(s1,s2)f表示列车f在客运站s1和客运站s2之间车站的停站次数，次。

列车的额外停站将会使旅客在列车上产生额外的等待时间，降低了旅客的快捷性，因此平均旅客额外停站次数越小，旅客的总旅行时间就越小，快捷性越好。

1.3 客座利用率

客座利用率为旅客周转量和客座公里之比，即用百分率表示的平均每一客座公里所完成的人公里数，可以由式(3)计算得到。

式中：Ve f为列车f在区间e上的载客人数，人；le为区间e的长度，km；Uf为列车f的定员人数，人；Ef为列车f运行径路上的区段集合。

客座利用率与开行列车数量有关，在一定的客流需求下，开行列车数量越多，客座利用率往往越低。客座利用率可以作为一个反映铁路旅客运输的舒适性的指标，客座利用率越高，越容易造成旅客拥挤，旅客的舒适性越低。

2 特定列车开行方案下线路通过能力利用评估

2.1 特定列车开行方案下线路通过能力利用情况评估流程

为了得到基于开行方案的服务水平与线路通过能力利用之间的关系，在客流OD一定条件下，需要生成一定数量服务水平不同的开行方案。作为列车开行方案的重要特征，停站结构和开行列车数量对通过能力利用和服务水平均产生影响。因此，为了体现不同开行方案的服务水平差异，在生成开行方案时可以采用以下2种策略，对开行方案优化模型的参数进行一定范围内的调整：1) 保持原有列车停站结构不变，改变开行列车数量(即下文开行方案模型的开行列车数量)；2) 保持开行列车数量不变，改变列车停站结构(即列车停站次数约束)。总的来说特定列车开行方案下线路通过能力利用评估可以分为以下关键步骤，如图1所示。

图1 列车开行方案的通过能力利用评估流程Fig.1 Flow chart of carrying capacity utilization evaluation of line plan

步骤1：以旅客OD量为输入，通过改变列车开行方案的参数，生成服务水平指标各不相同的列车开行方案，作为通过能力评估的数据输入；

步骤2：利用模拟编制列车运行图的方法，计算步骤1中得到的每个列车开行方案对应的通过能力利用率；

步骤3：利用式(1)至(3)计算步骤1中得到的列车开行方案的各项服务水平指标；

步骤4：分析得到特定旅客运输需求下服务水平指标与通过能力利用率的关系。

2.2 列车开行方案生成

2.2.1 行车组织条件假设

本文在研究中提出并遵从以下假设：1) 不考虑跨线列车开行，所有列车的运行径路相同；2) 不考虑旅客采用换乘的方式出行，即假设旅客从出发车站至到达车站只乘坐1列车；3) 所有列车的等级和编组相同；4) 列车运行的时间范围为6:00—24:00；5) 不考虑列车调度水平的影响；6) 不考虑车站通过能力的限制；7) 列车在各区段的纯运行时间、列车的起停附加时分已知且固定。

2.2.2 列车开行方案优化模型构建思路

结合本文的研究内容和假设，构建的列车开行方案优化模型的思路如下：1) 生成的开行方案需满足所有旅客的位移需求；2) 为了分析开行列车数量的影响，开行列车数量为模型的已知参数；3) 所有开行列车的等级、运行径路和编组相同，不存在权重的差别；4) 该模型的作用是确定列车的停站和客流分配，为分析服务水平和通过能力利用的关系提供实例。

2.2.3 符号说明

定义以下集合与元素：s为车站，S为车站集合；n为车站数量；为起始车站为s1终到车站为s2的区段上车站集合；φ(f)和μ(f)分别为列车f的始发站和终到站；Sf为列车f运行区段上车站的集合；e为区间；E为区间集合；Ef为列车f运行区段上区间的集合；α(e)和β(e)分别为区间e的起点站和终点站。

定义以下参数：m为开行列车的数量；βflower为列车f最少停站次数；βfupper为列车f最多停站次数；Uf为列车f的定员人数。

定义以下常数：M是一个较大的常数。

定义以下决策变量：q(s1,s2)为列车f运送从车站

f

s1到车站s2的客流量, 单位为人；Yfs为列车f在车站s停站的0-1变量，若列车f在车站s停站则取1，反之取0。

2.2.4 目标函数

考虑到在所有旅客的位移需求得到满足的情况下，列车的停站次数之和越少，列车的平均旅行速度通常越大，越有利于旅客运输的快捷性。因此，在列车开行方案优化模型中，以所有列车停站次数之和最小为目标函数，如式(4)所示。

2.2.5 约束条件

约束条件如式(5)至式(11)所示。

式(5)为客流量分配约束，表示对于一支OD客流必须分配至各次列车上，生成的开行方案不允许有未分配的客流。式(6)为列车定员约束，表示在列车运行的每个区间里，其实际的载客量均不能超过列车的定员。式(7)为列车停站次数约束，表示对于列车f，其在运行途中的停站次数需要在[βlowerf，βupperf]的范围内波动。式(8)为始发终到站必停站约束。式(9)表示列车在其运行区段范围外的车站必不停站。式(10)和式(11)为列车停站和客流分配的一致性约束，表示只有当列车在此车站停站，这次列车才能承载以此车站为旅行起点或终点的客流。式(12)至式(13)为决策变量可行域约束。该列车开行方案优化模型为一个混合整数规划模型，可以用商业求解软件进行求解。

2.2.6 考虑服务水平差异的列车开行方案生成策略

为了体现不同开行方案的服务水平差异而采用的2种策略的实现方式如下。

1) 保持原有列车停站结构不变，改变开行列车数量。在每次利用模型生成开行方案前，通过改变列车集合F中的列车数量m得到不同的开行方案。

2) 保持开行列车数量不变，改变列车停站结构。通过改变约束(7)中的βlowerf和βupperf参数，调整列车最大和最小停站次数，可以得到不同停站次数的列车开行方案。

通过以上2种策略，可以基于同一个OD客流需求，生成出多个服务水平各异的开行方案，作为后续通过能力利用评估的输入条件。

2.3 特定开行方案下线路通过能力利用评估

在得到多个服务水平各异的开行方案后，可以通过模拟铺画列车运行图的通过能力计算方法，计算各开行方案下线路通过能力利用情况。在开行方案给定的条件下，线路区段通过能力利用情况可由通过能力利用率来表示，即由当前列车开行方案中的列车数量与通过能力(即在当前列车开行结构下的最大列车开行数量)的比值得到。为此，本文采用李海鹰等[8]提出的压力测试和滚动分段求解的方法，即将一天的有效开行时间分成多个时间域，按照时间顺序“从前向后”依次求解每个时间域的决策变量，向时间域内不断添加列车直到无法在给定的时间内铺画所有列车为止，最终得到各开行方案下的满表列车运行图，并以该运行图上的列车数量作为列车开行方案对应的区段通过能力值。在满表运行图上存在2种列车，一种是开行方案中存在的列车，这些列车的总数表示通过能力中已被利用的部分；另一种是为了加压铺画满表运行图而插入的“虚拟列车”，这些列车的总数表示通过能力中未被利用的部分。由此可知，对应于某一特定开行方案的通过能力可以由式(14)表示。

式中：N实际为开行方案中开行旅客列车的数量，单位为列；N虚拟为满表运行图上虚拟列车的数量，单位为列。

区段通过能力利用率U区段可以由式(15)计算得到，单位为%。

基于压力测试和滚动分段求解的模拟铺画列车运行图的通过能力计算方法模型如式(16)~式(34)所示，该模型是一个混合整数规划模型，可以使用商业求解软件进行求解。在计算通过能力的过程中，为了避免由于给定停站方案的局限性无法得到满表运行图的情况出现，“虚拟列车”的停站也为模型的决策变量。

2.3.1 符号说明

定义以下参数：ETf和LTf为分别为列车f在始发站φ(f)的最早、最晚出发时刻；DTminf和DTmaxf分别为列车f的最小、最大停站时间；EndTf为列车f到达终到站μ(f)的最晚时刻；Re为列车f在区间e的纯运行时间；Ae和De分别为列车f在区间的起动附加时分、停车附加时分；IDD为列车出发间隔时间、IAA为列车到达间隔时间、IPP为列车通过间隔时间、IPD为列车通发间隔时间、IDP为列车发通间隔时间、IPA为列车通到间隔时间、IAP为列车到通间隔时间；Fv为“虚拟列车”的集合，Fm为所有列车的集合，因此满足Fm=F∪Fv；ysf为开行方案中列车的停站参数，取值与Yfs的解相同。

定义以下决策变量：asf为列车f到达车站s的时刻，单位：min；dfs为列车f在车站s出发的时刻，单位：min；Xfs为列车f的停站0-1变量，若列车f在车站s停站则为1，反之为0；Jfe,f′为列车区间运行顺序0-1变量，若列车f先于列车f′在区间e上运行取1，反之取0。

2.3.2 目标函数

以所有列车运行时间之和最小为目标函数，如式(16)所示。

2.3.3 约束条件

约束条件如式(17)～式(34)所示。

式(17)为列车停站时间约束，由列车停站时间的上限和下限构成。式(18)为列车到发时刻递推约束。式(19)为列车在区间运行先后顺序的逻辑约束。式(20)为列车在车站出发的时间与列车在区间运行先后顺序相适应约束，保证了列车在车站出发的时间和列车在区间运行先后顺序逻辑上具有一致性。式(21)为列车出发时间窗约束。式(22)为列车到达终到站时刻约束。式(23)至式(29)为列车间隔时间约束。式(30)至式(34)为决策变量可行域约束。

3 服务水平与通过能力利用率的相关性分析

本节以京广高速铁路上客流密度最大的长沙南—广州南区段下行方向为例，以该区段下行方向某年的日均OD客流、京广高铁线路参数以及列车运行标尺为已知数据，利用以上的方法生成多个具有不同服务水平的列车开行方案，然后分别计算这些开行方案的对应的服务水平指标和线路区段通过能力利用率，进而分析平均旅客服务频率、平均旅客额外停站次数、客座利用率和通过能力利用率的相关性规律。

本文采用Visual Studio 2019 的C#(.NET Framework 4.5.1)语言编写服务水平与通过能力利用率的相关性分析所需模型，并按图1的输入输出关系进行研究分析，其中调用整数规划求解软件Gurobi 9.0.1生成列车开行方案和求解基于压力测试法的能力计算模型，使用一台个人计算机(配置：CPU为i5-6300HQ，运行内存12 GB)运行模型的代码。

目前，长沙南—广州南区段下行方向每日开行列车数量为81～108列，列车的停站次数为2～7次。该区段上共有12个客运站，因此在生成列车开行方案时，单一列车的停站次数的数量约束在2次到12次之间调整。通过计算各区间的客流密度可知，至少开行84列旅客列车才能满足所有旅客的位移需求，否则无法生成可行的开行方案，因而开行列车数量在84列到137列之间调整。通过改变停站次数和列车数量，一共得到49个基于同一OD客流需求而服务水平存在差异的列车开行方案用于能力利用分析，各开行方案的服务水平指标值以及对应的区段通过能力利用情况见本文的OSID码。

3.1 平均旅客服务频率和通过能力利用率的关系分析

列车开行方案的平均旅客服务频率、开行列车数量和通过能力利用率的关系折线图如图2所示。每加开1列列车，平均旅客服务频率增加约0.48列，通过能力利用率增加约0.86%。在计划编制阶段，若平均旅客服务频率不能低于50列，开行方案编制人员依据上述结论可知在现有停站结构下至少开行102列列车才能满足平均旅客服务频率需求，而实现该服务水平，区段通过能力利用率不低于65.77%。图3为图2的侧视图，表明调节开行列车数量时，平均旅客服务频率与通过能力利用率存在明显的正相关关系。

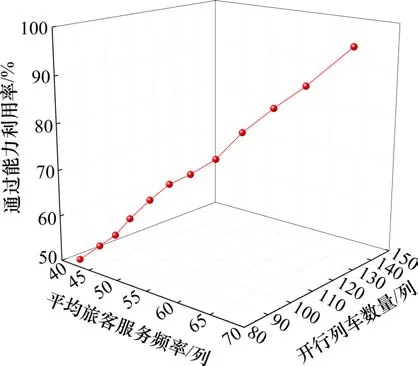
图2 平均旅客服务频率、开行列车数量与通过能力利用率关系折线图Fig.2 Line chart of the relationship between the average passenger service frequency, the number of trains in operation and the utilization rate of carrying capacity

图3 调节开行列车数量时，平均旅客服务频率与通过能力利用率关系折线图Fig.3 Line chart of the relationship between average passenger service frequency and utilization rate of carrying capacity when adjusting the number of operation trains

图4中各条折线表示开行列车数量分别为84列、94列、102列和116列时，平均旅客服务频率增加的同时通过能力利用率大体呈现“先增后减”(倒“U”字形)的变化趋势。这是由于在列车数量一定的条件下，平均旅客服务频率的增加只能通过增加列车的停站数量实现，而当平均旅客服务频率较低时(即各次列车的停站数量均较少时)，增加列车的停站会导致列车运行图的异质性逐渐增大，使通过能力的利用率增加；当列车的停站次数增加到一定程度之后，继续增加列车停站次数使得所有列车趋向成为“站站停”的列车，列车之间的异质性下降，列车之间的间隔时间减小，通过能力的利用率降低。

此相关关系提示计划编制人员，在确定列车停站次数时，可以借助图4快速评估当前的列车开行方案是否能够同时满足服务水平的要求和通过能力利用率的约束。例如，当列车开行数量在94～102列之间时，无论如何安排列车的停站方案，其通过能力利用率大致保持在60%～80%之间这一比较宽松的范围；当开行列车数量为110列，若平均旅客服务频率达到60列，通过能力利用率大致在74%～81%之间。

图4 调节停站结构时，平均旅客服务频率和通过能力利用率关系折线图Fig.4 Line chart of the relationship between average passenger service frequency and utilization rate of carrying capacity when adjusting the stop structure

3.2 客座利用率和通过能力利用率的关系分析

计算列车开行方案的客座利用率、开行列车数量和通过能力利用率关系折线图如图5所示，每加开1列列车，客座利用率大致降低0.634%，与此同时通过能力利用率约增加0.864%。在计划编制阶段，若客座利用率不能超过70%，开行方案编制人员依据上述结论可知至少开行109列车才能实现，而实现该服务水平，区段通过能力利用率不低于71.42%。图6为图5的侧视图，表明调节开行列车数量时，客座利用率与通过能力利用率存在明显的负相关关系。

图6 调节开行列车数量时，客座利用率与通过能力利用率关系折线图Fig.6 Line chart of the relationship between passenger seat utilization rate and utilization rate of carrying capacity when adjusting the number of operation trains

图7中各条折线表示开行列车数量分别为84列、94列、102列和116列时，客座利用率与通过能力利用率之间的关系。由于OD客流量是一定的，旅客周转量、开行列车数量不变时，客座利用率不变，但不同的停站方案对通过能力利用率的影响存在一些差异。计划编制人员可以根据图5的结论权衡客座利用率和通过能力利用，评估在给定客座利用率下通过能力利用率的大致分布范围。如客座利用率不能超过80%时，开行102列列车能够实现此需求，此时通过能力利用率在67.11%～81.6%之间。

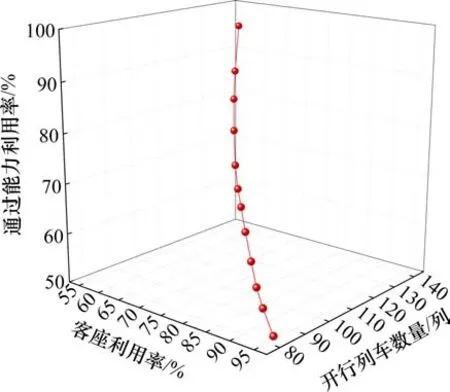
图5 客座利用率、开行列车数量和通过能力利用率关系折线图Fig.5 Line chart of the relationship among passenger seat utilization rate, the number of operation trains, and the utilization rate of carrying capacity

图7 调节停站结构时，客座利用率和通过能力利用率关系折线图Fig.7 Line chart of the relationship between passenger seat utilization rate and utilization rate of carrying capacity when adjusting the stop structure

3.3 平均旅客额外停站次数与通过能力利用率的关系分析

开行方案的平均旅客额外停站次数、开行列车数量与通过能力利用率的关系折线图，如图8所示。由图9和图8的侧视图可见，平均旅客额外停站次数和通过能力利用率存在一定的负相关关系，且随着开行列车数量的变化始终在0.05～0.10次的范围内波动。在计划编制阶段，开行方案编制人员可以依据上述结论得知现有停站结构下平均额外停站次数极少，调整开行列车数量对平均旅客额外停站次数几乎没有影响。

图8 平均旅客额外停站次数、开行列车数量与通过能力利用率的关系折线图Fig.8 Line chart of the relationship among the average number of additional stops of passengers, the number of trains in operation, and the utilization rate of carrying capacity

图9 调节开行列车数量时，平均旅客额外停站次数和通过能力利用率的关系折线图Fig.9 Line chart of the relationship between the average number of additional stops of passengers and the utilization rate of carrying capacity when adjusting the number of operation trains

图10中各条折线表示开行列车数量分别为84列、94列、102列和116列时，平均旅客额外停站次数、平均旅客服务频率和通过能力利用率之间的关系。由图11和图10的侧视图可见，列车开行数量一定时，平均旅客额外停站次数与通过能力利用率呈现“先增后减”(倒“U”字形)的变化趋势。在计划编制阶段，平均旅客服务频率一定时，平均旅客额外停站次数越大，通过能力利用率越小。如平均旅客服务频率需要达到54列时，平均额外停站次数范围在0.08～2.35次之间，通过能力利用率范围在57.53%～72.08%之间，由此可见，此时增加2.27次平均额外停站能降低14.55%的区段通过能力利用率。

图10 平均旅客服务频率、平均旅客额外停站次数和通过能力利用率关系折线图Fig.10 Line chart of the relationship between average passenger service frequency, average number of additional stops of passengers and utilization rate of carrying capacity

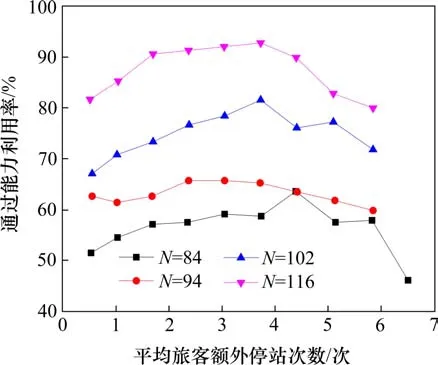
图11 调节停站结构时，平均旅客额外停站次数和通过能力利用率关系折线图Fig.11 Line chart of the relationship between the average number of additional stops of passengers and the utilization rate of carrying capacity when adjusting the stop structure

4 结论

1) 不同的列车开行方案对线路通过能力的影响较大，在运营阶段，客流结构和服务水平需求可能会发生变化，根据“按流开车”的原则需要调整列车开行方案，此时有必要考虑线路能力的约束和服务水平的影响。针对设计阶段的列车运行方案制定，本研究提出的方法也可以用于分析初、近、远期线路设计方案是否可以满足设计行车组织方案的能力要求，进而辅助设计人员在合理的能力利用下制定和评估不同时期列车开行方案。

2) 京广高速铁路长沙南至广州南区段下行方向的分析结果表明平均旅客服务频率、平均旅客额外停站次数以及客座利用率均与通过能力利用率存在定量关系。如列车停站结构一定时，区段通过能力利用率与平均旅客服务频率呈正比例关系、与客座利用率呈反比例关系等。这些关系能辅助开行方案编制人员快速准确地评估通过能力利用情况，以加速“开行方案制订(或调整)——能力约束校验”这一循环迭代的过程。

3) 本文提出的线路通过能力利用评估方法未考虑开行跨线列车产生的额外约束，如跨线列车在跨线车站有相对比较固定的上、下线时间窗，制约了列车在这些车站的到发时刻灵活度，可能会导致区段通过能力降低。为此，当高铁网络上开行一定比例的跨线列车时，为了有效利用繁忙线路的通过能力，铺画列车运行图时可以采取“先铺画繁忙干线，后铺画其他线路”的策略，但跨线客流的比例、分布等因素对服务水平有一定的影响。今后的研究可将跨线列车开行考虑在内，以完善考虑开行方案服务水平的通过能力利用评估方法。