基于线路参数估计的输电线路故障测距
冯 骁, 刘 骉, 孙 贺, 孔德健
(国网冀北电力有限公司 超高压分公司, 北京 102488)
0 引 言
电力与人们的生活息息相关, 同时也是国家经济发展的重要保障。高压输电线路具有传输距离长、损耗小、 负荷大的特点[1], 如果高压输电线路发生故障将会对一个地区的电力供应产生较大影响, 因此快速完成故障定位并消除故障对保障电力供应具有重要意义[2]。赵阳等[3]采用双端同步的测距方法, 利用最小二乘法实现线路参数录波同步的方法进行故障测距, 但该方法未考虑粗差对线路参数估计和测距结果精度的影响。陈霖等[4]提出了利用最小二乘法对线路参数进行估计从而实现同杆双回线路单线故障测距方法, 该方法同样没有考虑粗差对测距结果的影响。为此, 笔者利用Huber抗差估计优化总体最小二乘法, 解决了总体最小二乘法对线路参数估计过程中由于粗差存在造成的线路参数估计不准确的问题, 同时也提高了故障测距精度。
1 双端不同步法测距方程
输电线路在运行过程中发生的故障大多数都是单相接地故障[5], 因此笔者以单相接地短路故障为例对双端不同步测距方法进行分析, 假设输电线路处于对称状态运行, 并且为完全换位的均匀传输线, 单相接地故障的故障分量电路如图1所示。

图1 单相接地故障故障分量电路Fig.1 Single phase ground fault fault component circuit diagram
双端不同步测距法不需要输电线路两端的电压电流信号采样同步[6], 可存在不同步的角度δ, 从M端计算故障点的电压为

(1)

从N端计算故障点处的电压为
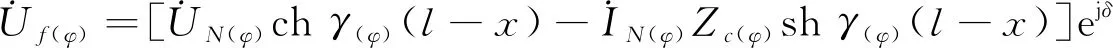
(2)
其中l为线路全长。
由于故障发生时, 故障点处的正序电压和负序电压分别相等, 可得出

(3)
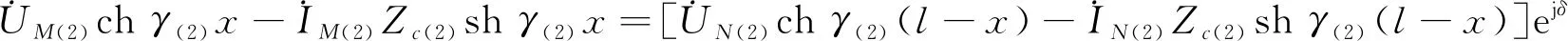
(4)
输电线路两端存在的角度差δ在线路正常运行状态下进行求解, 故障发生前用“q”表示, 其电路如图2所示。

图2 故障发生前电路Fig.2 Circuit diagram before fault
对图2进行分析可得出
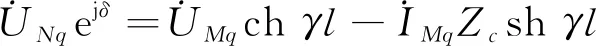
(5)
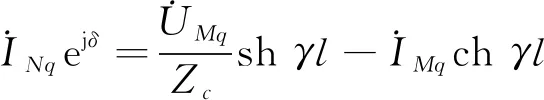
(6)
通过对式(5)和式(6)进行推导, 可得出线路两端的角度差

(7)

(8)
(9)
笔者利用Huber抗差估计优化的总体最小二乘法对其进行求解, 在求解之前需要选定未知数的初值, 线路参数值按照出厂值进行选择, 线路故障发生位置选择线路全长一半处, 线路两端的角度差值选择0°。
2 基于Huber抗差估计优化的总体最小二乘法
2.1 总体最小二乘法
总体最小二乘法相较于最小二乘法是一种较为先进的方法, 其同时考虑了测量误差和参数误差[7-8], 电力系统估计的数学模型为
z+ε=(H+EH)x
(10)
其中z为n×1维没有误差的测量真值;ε为随机噪声;H为n×m维无误差时参数矩阵真值;x为m×1维的待求量;EH为参数矩阵的随机误差。
总体最小二乘法的准则为
min[ε;EH]‖[EH;ε]‖F
(11)
其中‖‖F为Frobenius范数; [EH;ε]为n×(m+1)维的增广矩阵。对[H;z]进行奇异值分解可得
[H;z]=UΣVT
(12)
其中U=[u1,…,un]∈Rn×n;V=[v1,…,vn]∈R(m+1)×(m+1);Σ=diag(σ1,…,σm+1)且σ1>σ2>…>σm>σm+1。
当σm>σm+1且vm+1,m+1≠0时, 式(11)变为

(13)
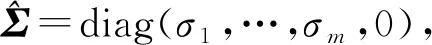
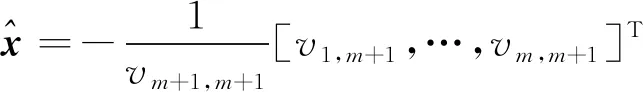
(14)
总体最小二乘法对输电线路信号容易产生的粗差没有抵御能力[9], 需要利用Huber抗差估计进行优化, 解决无法抵御粗差的问题, 从而提高线路参数估计的准确性。
2.2 Huber抗差估计优化
抗差估计就是选择合适的估计方法达到与实际情况相符的最佳估计值[10]。抗差总体最小二乘法与总体最小二乘法最大的不同体现在变权上, 如果与测量值相对应的残差超过了限定值, 需要对测量值对应的权值进行降权, 否则不对权值进行处理。
Huber分布是污染正态分布的一种, 其概率密度为

(15)
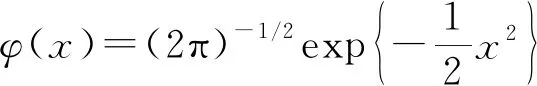
2Φ(c)-1+2φ(c)/c=1/(1-ε)
(16)
其中Φ(c)为φ(x)在区间(-∞,c)的积分。
在式(16)中给定ε值就能计算出c值, 在线路参数估计中经常遇到的粗差比例为1%~10%, 所以c值的范围在1.0~2.0之间,c通常取1.5,ε与c的关系如图3a所示, Huber分布密度曲线如图3b所示。
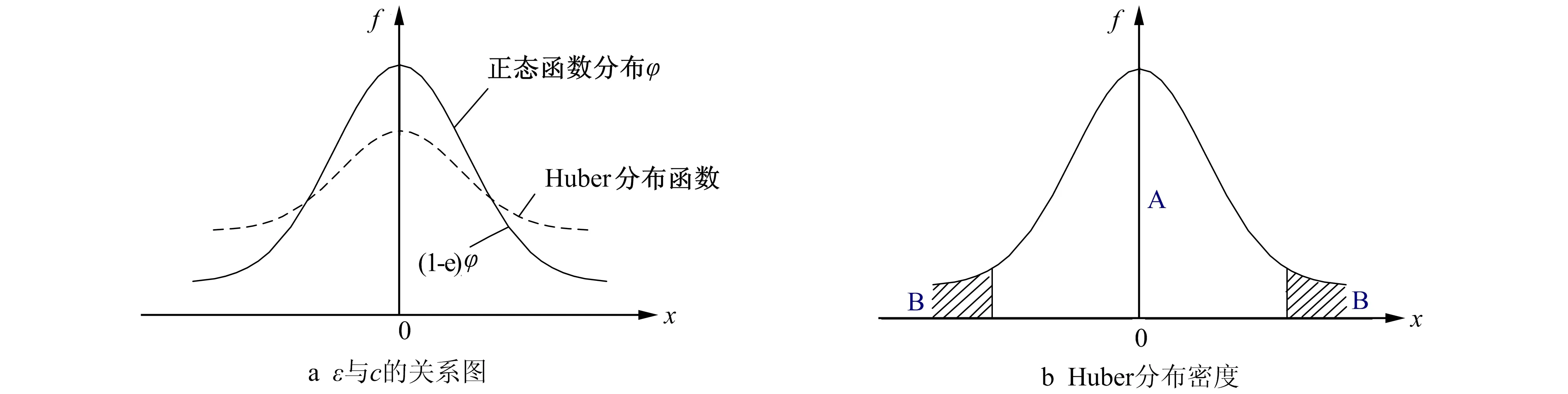
图3 污染率ε与对应值c关系图及Huber分布密度Fig.3 Pollution rate ε and corresponding value c relational graph and Huber distribution density
考虑参数矩阵H中含误差加权的模型

(17)
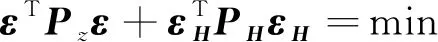
(18)
由拉格朗日极值条件可建立方程
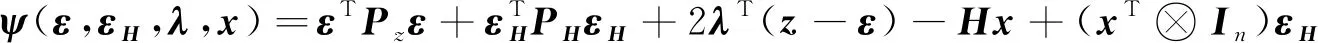
(19)
其中λ为拉格朗日乘子, 令(xT⊗In)=B, 对ε、εH、λ、x分别求导可得
将式(20)、 式(21)进行变换可得
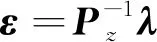
(24)
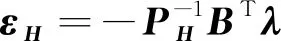
(25)
将式(24)、 式(25)代入式(22)可得

(26)
根据Huber权因子
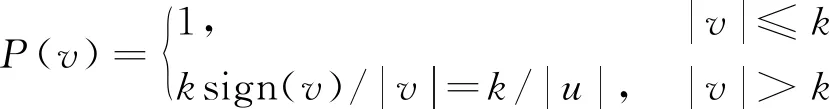
(27)
利用Huber抗差估计优化总体最小二乘法, 解决了最小二乘法对线路参数估计过程中由于粗差存在造成的线路参数估计不准确的问题, 从而提高了线路故障测距的准确度。
3 仿真分析
使用PSCAD(Power Systems Computer Aided Design)软件建立仿真模型, 并将仿真得到的故障数据导入Matlab软件中验证抗差总体最小二乘法测距的准确性。但利用仿真模型得到的电气量是同步的, 为验证双端不同步算法的准确性, 将仿真得到的线路两端电气量信号的不同步角设置为20°。线路仿真模型如图4所示。

图4 输电线路故障仿真模型示意图Fig.4 Schematic diagram of transmission line fault simulation model
笔者验证了发生概率达到90%以上的单相接地故障, 两相接地故障和相间短路故障的测距结果[11]。线路的实际参数为Rg=260.458 Ω/km,X=-11.685 Ω/km,β=4.246×10-5,α=1.036×10-3, 过渡电阻设置为100 Ω。单相接地故障、两相接地故障和相间短路故障的仿真结果分别如表1~表6所示。
对表1~表6进行分析可知, 总体最小二乘法在3种故障类型下线路参数估计的结果与实际值相差较大, 故障测距结果与实际故障位置的差值能达到0.526 km, 已经超出了一个档距范围。利用Huber抗差估计优化的总体最小二乘法线路参数估计结果更接近实际值, 故障测距结果与实际故障位置的差值最大为0.397 km, 最小值仅为0.003 km, 即便与实际位置的最大差值仍能保证在一个档距范围内。因此, 利用Huber抗差估计优化的总体最小二乘法在线路参数估计和故障测距方面都优于总体最小二乘法。

表1 基于总体最小二乘法的单相接地短路故障测距结果

表2 基于Huber抗差估计优化总体最小二乘法的单相接地短路故障测距结果

表3 基于总体最小二乘法的两相接地短路故障测距结果

表4 基于Huber抗差估计优化总体最小二乘法的两相接地短路故障测距结果

表5 基于总体最小二乘法的相间短路故障测距结果

表6 基于Huber抗差估计优化总体最小二乘法的相间短路故障测距结果
4 结 语
笔者采用双端不同步的测距方法, 利用Huber抗差估计优化总体最小二乘法, 解决了总体最小二乘法对线路参数估计过程中由于粗差存在造成的线路参数估计不准确的问题, 同时提高了测距精度。对短路故障中发生概率比较高的3种故障类型进行了仿真验证, 结果显示Huber抗差估计优化的总体最小二乘法在输电线路参数估计和测距精度方面都优于总体最小二乘法, 且故障测距精度能控制在0.5 km以内, 能满足现场要求。

