电动汽车无线充电阻抗匹配研究
付光杰, 毛远志
(东北石油大学 电气信息工程学院, 黑龙江 大庆 163318)
0 引 言
无线电能传输为电动汽车的充电技术提供了新的解决方案, 充电效率是无线充电亟需解决的问题, 目前有关提升充电效率的研究主要集中在提升耦合系数[1-2]和阻抗匹配两方面。电动汽车底盘高度一般在15~20 cm之间, 适用于电动汽车无线充电的方式为磁耦合谐振式无线电能传输[3]。在S-S型磁耦合谐振式电动汽车无线充电系统中, 存在一个最优负载, 当实际负载在此值附近时, 传输效率会取到最大值[4]。适用于汽车的动力电池一般为锂离子电池[5], 其型号存在较大区别, 因此负载阻抗会有较大变化, 进而导致系统传输效率降低。所以进行负载的阻抗匹配, 使系统传输效率始终维持在较高水平十分必要。
负载阻抗匹配分为有源阻抗匹配和无源阻抗匹配两种形式, 无源阻抗匹配通过电感, 电容组成的阻抗调节网络实现阻抗匹配[6]。但是这种方法只能实现某个运行点的阻抗匹配, 无法实现对最大效率点的动态跟踪。有源阻抗方法则是利用附加的DC-DC变换器实现对等效阻抗的动态调节[7]。单独采用buck变换器或boost变换器阻抗调节范围有限[8], buck-boost变换器虽然阻抗调节范围变宽[9], 但功率损耗较大。笔者选用双管buck-boost变换器既满足调节范围的要求, 功率损耗也相对较小。在最大效率追踪时, 程连斌[10]采用负载端恒压输出的控制策略, 当电阻增大时, 输出功率急剧下降。笔者通过逆变器闭环移相控制, 使不同阻值的负载能输出预设的对应电压, 输出功率保持不变, 解决了电阻增大时功率下降的问题。
1 S-S型磁耦合谐振式系统传输效率分析
笔者通过互感理论研究磁耦合谐振式无线电能传输机理。传统的拓扑结构根据补偿电容在电路中的位置大致分为4种: 串-串(S-S)、 串-并(S-P)、 并-并(P-P)和并-串(P-S)。徐晨洋等[11]将4种拓扑结构的电动汽车无线充电系统进行建模与分析, 结果表明S-S型系统的电压增益与谐振补偿网络更加稳定, 实际应用价值更高。因此笔者选用S-S型拓扑结构, 基于互感理论搭建了系统的仿真模型。S-S型磁耦合谐振式拓扑电路如图1所示。

图1 S-S型谐振网络等效电路Fig.1 Equivalent circuit of S-S resonant network
图1中发射与接收谐振器的谐振频率为ω。C1、C2,R1、R2,L1、L2,I1、I2分别为发射线圈、 接收线圈的补偿电容, 内阻, 自感, 电流。ZL为负载回路的阻抗,Uin为前级感应电压源,M为互感。根据基尔霍夫电压定律, 得到两线圈结构的回路方程

(1)
令

(2)
可求得I1,I2的表达式, 然后得到负载功率及输入有功功率表达式, 二者相除即为传输效率

(3)
比较式(3)的分母可知, 当发射线圈和接收线圈同时发生自谐振, 此时Z1=R1,Z2=R2+ZL, 分母取最小值, 传输效率取得最大值。则谐振耦合能量无线传输效率为
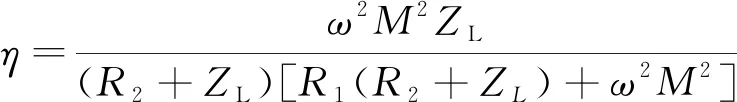
(4)
笔者只研究负载为纯阻性负载时的阻抗匹配问题, 因此下文中ZL用RL代替。
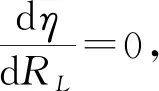
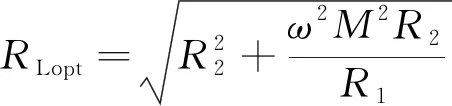
(5)
当RL取得此值时, 系统传输效率最大。
2 双管buck-boost阻抗匹配电路及最大效率追踪
2.1 双管buck-boost阻抗匹配电路
根据上述分析, 系统存在一个最优负载, 使系统传输效率达到最大。笔者使用双管buck-boost变换器阻进行阻抗匹配, 如图2所示。与单管buck-boost变换器相比, 双管buck-boost变换器输出电压与输入电压同极性[12], 且有两只管子承受输入电压, 使耐压值更高。

图2 双管buck-boost阻抗匹配电路Fig.2 Dual-switch buck-boost impedance matching circuit
设Re为整流桥后端的等效电阻, 开关管Q1和Q2的驱动信号占空比分别为D1和D2。在电流连续工作模式下, 根据双管buck-boost变换电路的电压和电流关系得到整流桥后端的等效电阻表达式为

(6)
对二极管全桥不可控整流电路,其输出的方波经傅里叶分解后得到其输出电压的基波幅值为
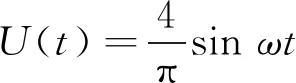
(7)
所以整流桥前端等效电阻和后端等效电阻关系为
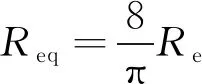
(8)
由此得到系统等效电阻为
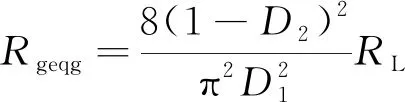
(9)
由文献[13]可知双管buck-boost变换器存在多种控制方式。占空比相同时, 当两管驱动波形相位差为π或2π(1-D)时, 电感电流脉动最小, 效率最高, 其中前者又称为交错调制, 后者称为双沿调制。考虑到交错调制实现更为简单, 因此笔者使用交错调制方式。此外, 变换器还可以分别工作在buck模式或boost模式, 这种控制方式称为两模式控制。在这种控制方式下任何时刻都只有一只开关管处于工作状态, 另一只要么关断, 要么一直导通。两模式控制方式下变换器传输效率最高, 但在涉及到模态切换时, 控制策略复杂。与无线充电系统的兼容性不佳, 所以笔者采用单模式控制方式。
2.2 最大效率追踪
由上述分析可知, 当电阻阻值变化时, 只要相应地调节双管buck-boost变换器的占空比, 使等效负载Req和系统最优负载RLopt相等, 传输效率即可维持在最高水平, 实现系统的最大效率追踪。笔者采用两管占空比相同方式下的单模式交错调制, 即D=D1=D2,令Req=RLopt, 可得

(10)
3 逆变器移相控制和恒功率输出
笔者通过双管buck-boost变换器的开环控制进行最大效率点的追踪, 负载端电压不能维持稳定输出, 为此, 可对前级全桥逆变电路采用闭环移向控制。笔者提出一种恒功率输出的控制策略, 即在保持输出功率恒定的条件下, 根据不同的负载阻值设定对应的参考输出电压并给到控制器。通过无线充电系统前级的全桥逆变电路的闭环移相控制方式即可稳定输出对应电压, 实现恒功率输出。
3.1 恒功率输出控制方式
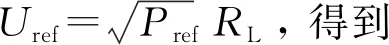
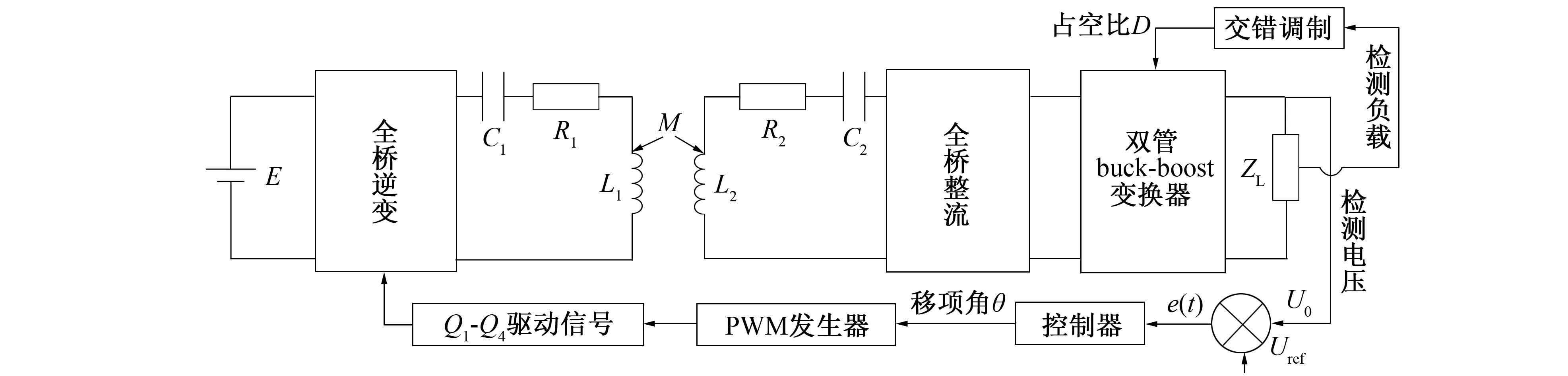
图3 系统控制结构框图Fig.3 Control structure block diagram of the system
3.2 逆变器移相控制

图4 移向控制示意图Fig.4 Phase shift control schematic
移相控制时, 全桥逆变器4只开关管Q1,Q2,Q3,Q4的占空比均固定为0.5, 右侧桥臂Q3的触发信号比左侧桥臂Q1的触发信号滞后角度为θ, 如图4所示。设逆变器前侧的直流电压源的幅值为E, 逆变器输出的方波电压基波幅值为

(11)
由式(11)可知, 在0~180°的移向范围内, 逆变器输出电压以正弦规律逐渐增大, 当负载阻值变化时, 通过移相角可以改变输出电压, 进而控制功率。
4 仿 真
为验证方案的可行性, 笔者在Simulink中对无线充电系统进行了建模仿真, 图5为搭建的仿真模型。仿真具体参数取值如表1所示。
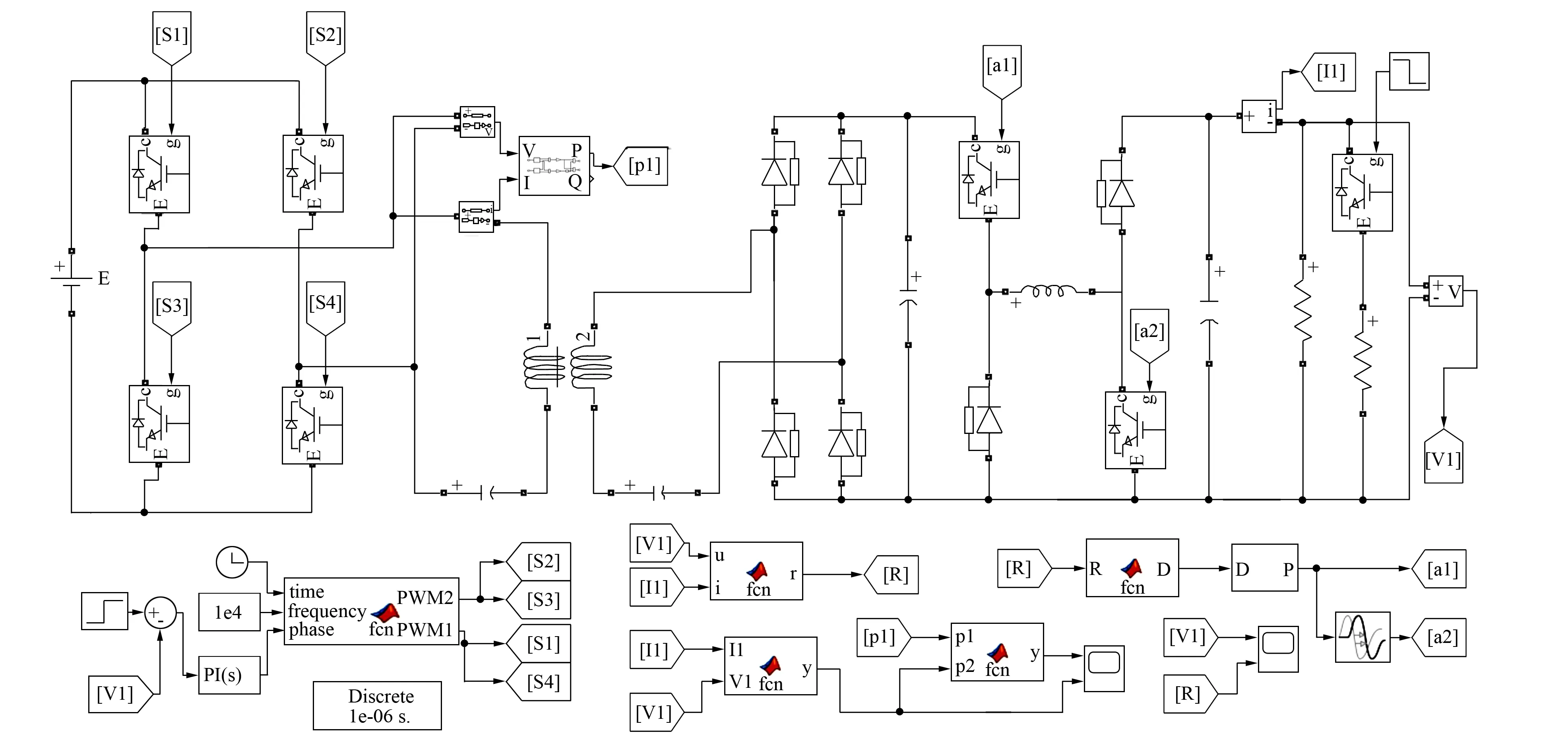
图5 双管buck-boost阻抗匹配的无线充电仿真电路Fig.5 Wireless charging simulation circuit with dual-switch buck-boost impedance matching
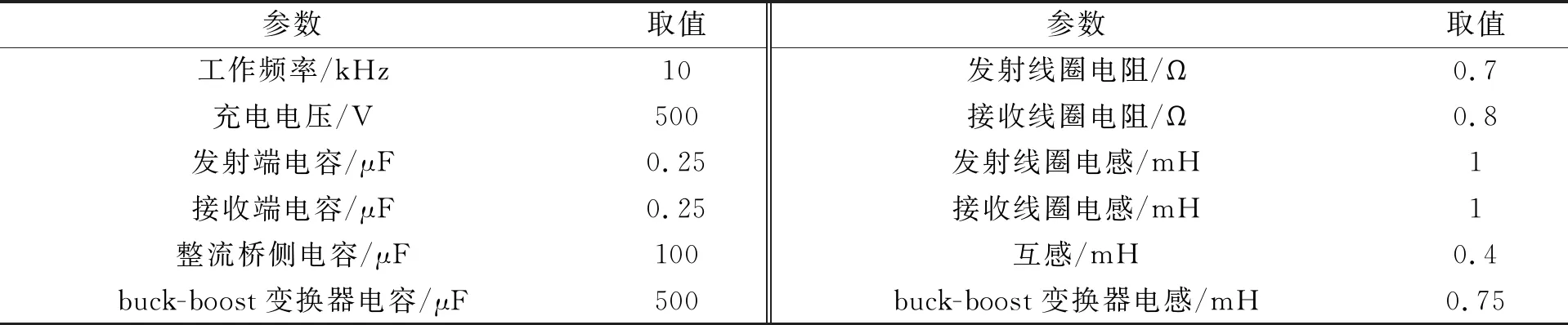
表1 仿真参数
当未进行阻抗匹配时, 电阻阻值从5 Ω逐渐增大到50 Ω时, 系统的传输效率如图6所示。由图6可知, 当电阻逐渐增大时, 系统传输效率先升高后降低, 负载为23 Ω时, 传输效率取得最大值。

图6 传输效率与随负载电阻变化示意图Fig.6 The relationship between transmission efficiency and load resistance
加入双管buck-boost变换器, 设定系统期望输出功率为4 200 W, 当负载电阻变化时, 输出电压, 传输效率和输出功率的波形图如图7和图8所示。

图7 输出电压波形图Fig.7 Output voltage waveform
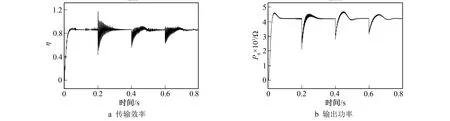
图8 传输效率和输出功率波形图Fig.8 Transmission efficiency and output power waveforms
仿真结果表明, 当负载阻值在0.2 s从10 Ω跳变到20 Ω, 0.4 s从20 Ω跳变到30 Ω, 0.6 s从30 Ω跳变到40 Ω时, 输出电压经过约0.1 s的小幅波动后, 均能稳定输出对应的期望电压, 传输效率经过约0.1 s的小幅波动后始终维持在85%, 输出功率经过约0.1 s的小幅波动后维持在4 200 W。仿真结果证明了逆变器的闭环移向控制能实现无线充电系统的恒功率控制; 因为加入的阻抗匹配电路有额外的功率损耗, 阻抗匹配后的传输效率与未匹配前最优负载时的传输效率相比略有降低, 但当负载阻值与最优负载阻值相差较大时, 传输效率提升较为明显, 总体上双管buck-boost变换器的加入实现了系统的最大效率追踪。
5 结 语
针对电动汽车无线充电系统由于电池阻值的变化导致系统传输效率不能维持在最高水平的问题, 笔者通过在负载端接入双管buck-boost变换器, 在综合考虑不同调制方式下的功率损耗和控制策略的复杂性基础上, 采用单模式交错调制的控制方式, 实现了最大效率追踪。同时通过逆变器的闭环移向控制, 对不同的负载阻值设定不同的参考电压, 实现了恒功率输出, 避免了恒压输出时输出功率随负载阻值变大急剧下降的问题。

