基于粒子滤波的微地震信号去噪方法

李学贵, 高 明, 吴润桐, 王如意,訾乾龙, 鉴 振, 李文森, 周英杰

(1. 东北石油大学 a. 计算机与信息技术学院； b. 人工智能能源研究院；c. 黑龙江省石油大数据与智能分析重点实验室, 黑龙江 大庆 163318；2. 大庆油田采油工程研究院 钻井室, 黑龙江 大庆 163453; 3. 中国石油集团 工程技术研究院有限公司, 北京 102206)

0 引 言

随着油气资源需求量的增加, 对油气资源开采技术的要求也不断提高。微地震监测在油气资源开采领域是一项重要技术, 通过微地震监测技术, 实时监测在油气开发过程中地下压裂情况[1], 及时调整压裂参数, 可有效提高油气开发的产量, 降低开发成本。微地震信号的获取是微震监测的重要步骤, 但微震信号存在持续时间短、 能量低等缺点[2], 同时由于环境的复杂性, 获得的微震信号总是伴随着很多噪声, 难以对其进行应用研究。微地震噪声水平对微地震资料在实际应用中的可靠性和准确性有较大影响。因此, 需要采用一些方法提高微地震信号的信噪比(SNR: Signal Noise Ratio), 从而提取出微地震资料中所需要的因子。

目前应用于微地震数据去噪的方法有很多, 根据微地震的监测方式, 将去噪方法分为两大类： 一类是井中微地震资料去噪, 另一类是地面微地震去噪[3-4]。传统滤波常用于去噪, 如高通与低通滤波、 带通滤波、 带阻滤波、 均值滤波和中值滤波等[5], 其通过衰减一些高频和低频成分提高信噪比。但由于在很多情况下信号和噪声共享一些频带, 所以在去噪过程中, 一部分有用的信号资料被滤除, 同时噪声并没有完全去除, 而且带通滤波器会使部分信号失真。虽然传统滤波可提高信噪比, 但其去噪效果不稳定[6]。除了常用的传统滤波外, 还有曲波变换[7]、 Shearlet变换[8]、 单道SVD变换[3]、 经验模态分解[9]和字典训练小波域稀疏表示[10]等方法, 但这些去噪方法较为单一, 处理信号能量较弱的微地震信号效果不佳。

目前, 卡尔曼滤波已应用于微地震信号去噪中, Baziw等[11]利用卡尔曼滤波, 通过逐渐减弱震荡周期模拟微地震信号的子波, 对微地震数据进行建模并处理。与基于数据的去噪方法相比, 基于模型的卡尔曼滤波去噪需要的数据量较少, 同时对真实信号的损耗较小。并在原有基础上改进了检测微地震P波初至的卡尔曼滤波器的设计, 进一步提高了卡尔曼滤波识别P波初至的能力。但卡尔曼滤波只能处理线性系统, 而微地震信号通常是非线性的, 只能通过线性化处理后再通过卡尔曼滤波去噪。这种方式会损失微地震信号的真实性。

与卡尔曼滤波相比, 粒子滤波适用于解决非线性非高斯的滤波问题, 更加适合处理微地震信号。该方法的基本思想是用一组粒子当作样本近似表示系统的后验概率分布, 然后用其近似的表示估计非线性系统的状态。

针对微地震信号能量弱和持续时间短等缺点, 笔者提出了一种基于粒子滤波的微地震信号去噪方法。该方法能有效保留微地震信号, 提高去噪效果。通过模拟微地震数据和真实微地震数据测试, 与传统小波阈值方法相比, 该方法去噪效果更好, 实用性较高。

1 基本原理

1.1 粒子滤波

粒子滤波是一种基于蒙特卡洛模拟的贝叶斯滤波算法[12]。其通过构造数量足够多的粒子, 并将粒子设置对应权值, 通过构造的粒子样本得到状态量的后验概率密度。这种方法通过转变求和的方式近似求解非线性系统中的高维积分, 从而得到状态量的最小均方误差估计, 而粒子数量N→∞时, 就可以无限接近概率密度分布。粒子数目越多, 滤波所估计的后验概率密度越接近真实的后验概率密度, 从而达到最优贝叶斯估计。

粒子退化是粒子滤波算法中一个缺陷, 其是在算法的迭代过程中很小一部分的粒子权值很大, 而剩余大部分的采样点权重非常小, 使后面的过程中近似后验概率密度误差较大。重采样方法有效解决了粒子退化问题, 其通过对权值较大的粒子进行复制, 替换权值较小的粒子, 从而得到新的样本集合, 并将得到的新粒子的权重均设为1/N, 重采样的过程通过提高粒子的多样性, 解决了单一样本集难以估计的问题。

标准的粒子滤波算法就是在序贯重要性采样算法中加入重采样思想, 将微地震信号去噪问题通过递归状态估计得出, 假设描述非线性动态系统的状态空间模型为

xk=f(xk-1)+wk-1

(1)

yk=h(xk)+vk

(2)

式(1)和式(2)分别是状态方程和观测方程, 系统状态空间模型如图1所示。其中xk为k时刻系统的状态,xk-1为上一时刻的系统状态,yk为k时刻系统状态的测量值；f(·)为状态函数,h(·)为测量函数；wk为系统的过程噪声,vk为测量噪声,wk与vk相互独立。

图1 系统状态空间模型Fig.1 System state space model

1.2 贝叶斯滤波

贝叶斯滤波具有预测和更新两个过程, 首先对模型进行预测得出先验概率密度p(xk|y1 ∶k-1), 再根据测量值y1 ∶ k={y1,y2,…,yk}对先验概率密度进行修正, 递推估计出k时刻状态变量xk的值, 得出后验概率密度p(xk|y1 ∶k)。

预测方程为

(3)

更新方程为

(4)

其中p(xk|xk-1)和p(yk|xk)分别由状态方程和观测方程得出,p(yk|y1∶k-1)为归一化常数, 即

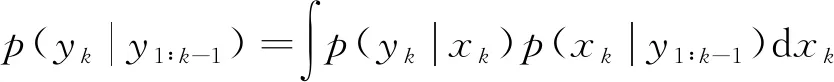
(5)

再根据

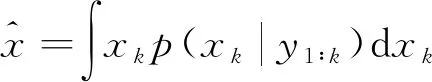
(6)

则可计算出最小均方差意义下的最优估计。

贝叶斯理论利用新的测量值修正先验概率密度, 从而得出后验概率密度。先验概率密度与前一时刻状态有关, 而后验概率在更新后更加接近系统的真实状态。但由于高维积分运算的存在, 对一般的非线性非高斯的估计问题, 直接利用贝叶斯公式很难进行求解。所以粒子滤波基于蒙特卡洛的滤波方法解决线性滤波问题时, 通常使用一种序贯重要性采样的算法(SIS: Sequential Importance Sampling)[13], 该方法从建议分布中提取粒子, 每个粒子有相应的权值。

1.3 重要性采样

根据蒙特卡洛近似思想, 可通过将粒子加权求和的方式求出后验分布

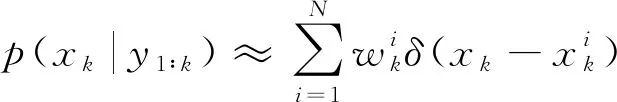
(7)

其中δ(·)为Dirac-delta函数。

但直接对后验概率密度进行抽样很难实现, 因此需要根据更容易采样的重要性分布q(xk|y1 ∶k)进行采样, 采样得到粒子集后进行加权求和近似表示后验分布p(xk|y1 ∶k)。

任意函数φ(x)用贝叶斯公式可表示为

(8)

求和形式为

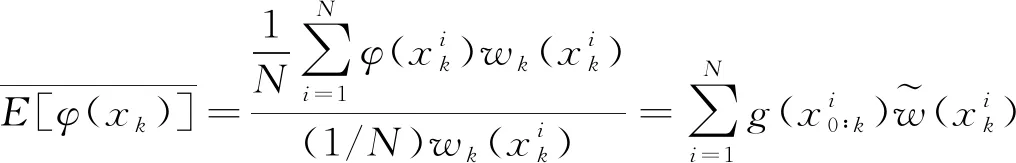
(9)

第i个粒子的权值表示为

(10)

在给定重要性分布函数q(xk|x0∶k-1,y1∶k)的条件下, 可按照式(10)递推计算重要性权值。

序贯重要性采样方法通过递归的方式求解重要性权值, 其中

q(xk|y1∶k)=q(xk|x0∶k-1,y1∶k)q(x0∶k-1|y1∶k-1)

(11)

将式(11)代入式(10), 得出重要性权值

(12)

归一化权值为

(13)

1.4 重采样

序贯重要性采样存在一个缺陷, 即随着算法的不断迭代, 大多数粒子的权值会变得很小, 只有少数或个别粒子的重要性权值会变得很大, 这种现象即为粒子退化。粒子退化会致使粒子集表达的后验概率密度误差较大, 降低估计的精度。1993年, Gordon等[14]将重采样算法引入序贯重采样中, 其思想是增加权值较大粒子的数量, 减少权值较小粒子的数量, 从而更贴近后验概率密度。但重采样方法同样也存有缺陷, 由于需要复制粒子, 会增加算法的时间； 同时如果只留下少数权值较大的粒子, 就会丧失粒子的多样性。所以, 需要对粒子退化程度进行判断, 分析是否需要进行重采样, 常用的准则是有效粒子数Neff, 定义如下

(14)

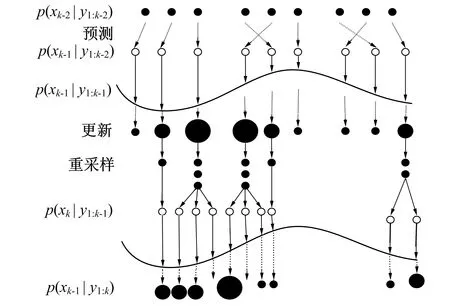
图2 粒子滤波算法过程Fig.2 Process diagram of particle filter algorithm

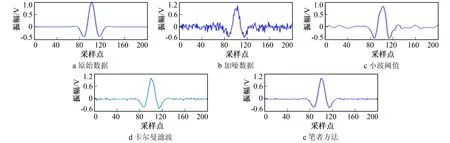
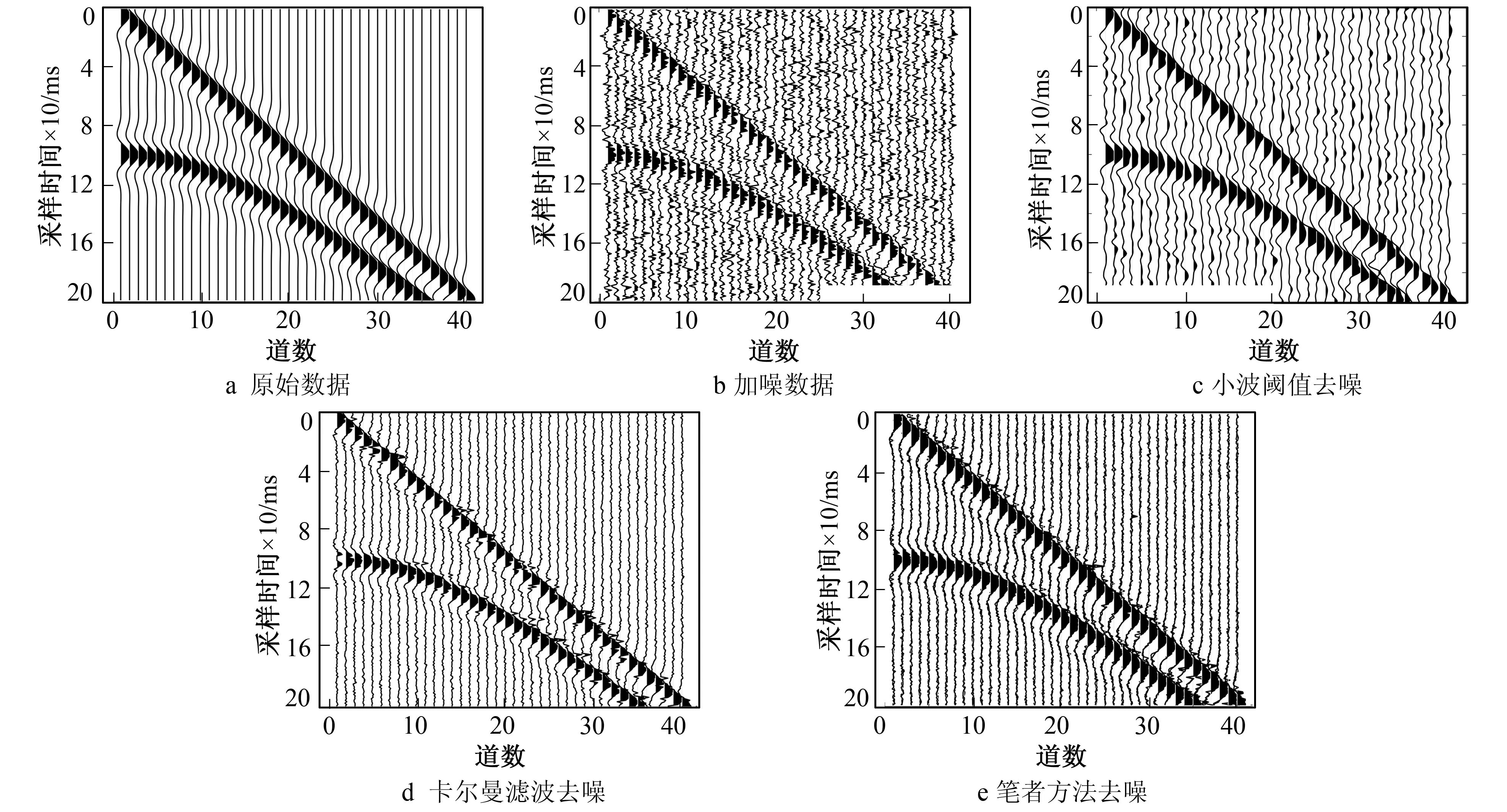
其中Neff为在序贯重要性采样后粒子的退化程度, 其数值越小, 粒子退化越严重。通常先预设一个阈值Nth, 如果Neff

1.5 微地震信号建模

平稳线性时间序列分析中, 常用的时序模型包括自回归(AR: Auto-Regressive) 模型、 滑动平均(MA： Moving Average)模型和自回归滑动平均(ARMA： Auto-Regressive Moving Average)模型[15]。其中AR模型描述系统对过去自身的记忆, MA模型描述系统对过去时刻噪声的记忆, 而ARMA模型则是系统对过去自身状态以及各个时刻噪声的记忆。通过这几种模型可描述的随机现象很广, 并且建模后模型的拟合精度较高。

相比于其他时间序列模型, AR模型算法是一种较为简单的线性预测模型, 具有计算简单、 自适应性能较强等优点。因而, 该模型被广泛地应用于多个工程领域中的时序预测或信号分析[16]。其通过利用前期随机变量的线性组合描述后期随机变量, 对给定的时间序列{x,i=1～N}, AR模型的标准形式为

xt=φ1xt-1+φ2xt-2+…+φpxt-p+at,t=p+1,p+2,…,N

(15)

其中p为模型阶数,φ=(φ1φ2…φp)为AR模型系数。AR模型主要参数为模型阶数p和模型参数φ=(φ1φ2…φp)。根据实际应用的模型数据, 以及相关参数估计方法和定阶准则, 得到AR模型阶数及参数。

2 仿真实验

2.1 模拟数据

为验证笔者方法的去噪性能, 通过建立模拟单道数据, 加入随机噪声进行试验。图3a为未加噪数据, 图3b为加入高斯随机噪声数据, 加入噪声后信噪比SNR为-4.773 6 dB, 然后分别用笔者提出的小波分块阈值方法和传统小波阈值方法进行去噪。图3c和3d分别为传统小波阈值和卡尔曼滤波处理结果, 图3e为笔者的分块阈值处理结果, 图4为单道数据去噪对比图, 图5为单道数据频谱图, 传统去噪后SNR为0.184 5 dB； 卡尔曼滤波去噪后SNR为0.484 1 dB； 笔者方法去噪后SNR为0.757 8 dB。信噪比

(16)

其中Ps为信号能量,Pn为噪声能量。

图3 模拟单道数据Fig.3 Simulated single channel data

图4 模拟单道数据去噪前后对比 图5 模拟单道数据频谱图 Fig.4 Comparison of simulated single channel data before and after denoising Fig.5 Spectrum of analog single channel data

通过建立多道模拟微地震数据并对其进行分析。图6a为多道模拟微地震数据, 图6b为加入噪声后的模拟数据, 信号信噪比为-0.148 1 dB。通过图6a和图6b可知, 噪声对有效信号影响较大。通过传统小波阈值和卡尔曼滤波处理后SNR分别为6.857 4 dB和7.145 2 dB, 而通过笔者方法处理后SNR为8.295 3 dB。通过图7的对比可看出, 加入噪声的图像噪点密集, 经过小波阈值去噪后真实信号仍然难以辨别, 而经卡尔曼滤波去噪后, 信号波形较为清晰, 一部分随机噪声被去除, 但仍存留部分噪声对信号产生干扰, 去噪效果不如笔者方法。通过从图6和计算得到的信噪比可以得出, 小波阈值方法和卡尔曼滤波虽然对信号中的噪声具有一定的滤除作用, 但仍存在部分噪声, 同时损失了部分真实噪声。与传统小波阈值和卡尔曼滤波相比, 笔者方法不仅有效滤除噪声, 提高了信噪比, 同时更有效保存了真实信号, 避免了真实信号的损失, 去噪后得到的结果更接近真实信号。不同方法去噪结果对比如表1所示。

图6 模拟多道数据Fig.6 Analog multichannel data

表1 不同方法处理模拟微地震数据对比

2.2 实际微地震数据

图7为真实微地震资料的剖面图。

为验证这种去噪方法的实际效果, 笔者从真实的微地震数据中截取了一部分作为实验数据。数据共27道和700个采样点, 采样间隔为1 ms。真实数据对比如图8所示。从图8a可看出, 此微地震资料结构复杂, 存在大量干扰性的噪声, 信噪比低。图8b和图8c分别为经过小波阈值和卡尔曼滤波处理后的结果。

为更直观地分析实验结果, 单独截取第4道数据, 进一步对去噪前后的微地震信号波形进行分析(见图9), 通过波形分析可观察到有效信号的波形变化情况以及所处的位置。由图9可见, 原始信号的波形受到随机噪声的干扰, 变得非常混乱, 无法有效区别有效信号与噪声信号。通过传统小波阈值方法去噪后, 虽然噪声有一定消减, 但仍有较大干扰。

图8 真实数据对比Fig.8 Real data comparison

图9 单道波形分析Fig.9 Single channel waveform analysis

经卡尔曼滤波处理后, 一部分噪声被滤除, 但仍存有扰动较弱的噪声。通过笔者方法去噪处理后, 噪声信号被大幅消减, 有效微地震信号得以显现, 信号发生在450～500 ms之间, 幅值在-1～1之间。

通过对比可以看出, 传统小波阈值和卡尔曼滤波具有一定的去噪效果, 能滤除大部分噪声, 但对真实地震信号造成一定损伤, 影响后续的研究； 而笔者方法不仅有效去除了绝大部分噪声, 同时更好地保留了有效信号, 提高了信噪比, 相比较传统小波阈值方法的处理效果更好。

3 结 语

笔者提出了一种基于粒子滤波的微地震信号去噪方法, 该方法通过参数建模的方式对信号进行分析, 处理结果精度较高。粒子滤波针对非高斯、 非线性信号具有优势, 不需要非线性化处理信号, 并通过对参数建模的方式对信号进行分析, 从而减少了信号的损失。将该方法应用于模拟微地震数据和真实微地震数据中, 实验结果表明, 该方法在不影响信号相位或极化信息的情况下, 更好地保留了真实信号, 有效提高了波形的信噪比, 优于传统的小波阈值去噪方法和卡尔曼滤波去噪方法。而此方法的不足之处在于, 基于模型的去噪方法效果受建模准确性的影响, 若建模误差较大会导致去噪效果变差, 并且需根据噪声数据特定选择建模方法。因此, 设计更好的建模方法及提高建模准确度是今后的研究方向。