红外气体传感教研系统的信息度量方法
郑传涛, 马琰铭, 刘大勇, 刘 洋, 宋 芳
(吉林大学 a. 电子科学与工程学院; b. 通信工程学院, 长春 130012)
0 引 言
“信息论”是电子学科研究生专业的必修课程, 揭示了信息的本质特性和规律, 其主要研究如何提高信息系统的可靠性、 有效性、 保密性和认证性, 以及使信息系统最优化[1-3]。近年来, 在信息理论的指导下, 信息技术不断发展, 在自然科学与社会科学等领域也有所延伸, 诞生了如光学信息论、 医学信息论等新分支、 新领域[4-5]。信息论将信息的传递作为一种统计现象考虑, 因此具有一定的普适性, 对其他学科的发展具有一定的指导意义[1,6]。
在教学方面, 学习信息论的基础是理解信息的概念和掌握基于概率统计的信息度量方法, 因此需要从感性的认知和严谨的数学推导两个层次入手。在传统的信息论教学中, 基本概念、 公式推导和习题讲解占据课堂的主体部分, 而缺乏对信息论具体应用的直观讲解。因此, 针对信息论教学中该环节的缺失, 发挥信息论对信息本质研究的指导作用, 需要建立一套能辅助讲解信息论有关概念、 且实验现象直观的教研系统。在科研方面, 波长调制光谱技术是一种高灵敏的吸收光谱技术, 具有选择性好、 寿命长、 精度高和灵敏度高等优点, 并能实现对待测气体的实时检测[7-8], 近年已成为衡量气体检测领域的研究热点。该技术在扫描气体吸收线的同时使用高频正弦波调制可调谐激光二极管, 通过对光电探测器的输出信号进行正交锁相放大处理, 得到正比于气体浓度的谐波信号。测量过程伴随着信息的传输, 根据信号不增性原理, 探测到的信号相对于真值发生了信息的损失, 这意味着测得数据的有效性受损[4,6,9]。为定量评估测量数据的有效性, 需要在建立系统数学模型的基础上通过信息论的有关理论对传感信息进行评估。因此, 建立红外气体传感系统的信息度量方法在科研方面也具有重要意义。
针对信息论教学需求以及波长调制光谱技术理论分析和科研需要, 笔者采用Matlab软件建立了波长调制光谱技术的理论模型, 仿真了激光调制、 气体吸收、 光电转换和谐波提取等各个环节。结合信息论中噪声熵、 信道传输矩阵、 信息传输效率等相关原理, 定义了最小可分辨的浓度间隔。根据波长调制光谱技术理论模型, 评估了系统噪声的主要来源, 研究了系统噪声对最小可分辨间隔的影响。根据系统实际测量数据, 计算了系统的最小可分辨间隔。应用实践表明, 该红外气体传感信息度量教学科研系统及相关方法, 满足了信息论课程教学要求以及波长调制光谱技术的科研需要, 取得了较好的教学与科研效果。
1 波长调制光谱技术建模与仿真
如图1a所示, 红外气体传感系统通过测量实际气体浓度(假设为X), 得到测量浓度(假设为Y), 由于传感系统受光学、 电学等噪声的影响, 测量浓度Y呈现一定的随机性。因此通过Y得到的关于X的信息与其客观存在的信息并不严格相等, 即造成了传感信息的损失。红外吸收光谱法具有灵敏度高、 响应速度快和非接触测量等优点, 可调谐二极管激光吸收光谱技术是一种经典的红外吸收光谱检测技术[8]。控制激光波长扫描气体的特征吸收谱线, 当激光与待测气体相互作用时, 根据朗伯-比尔定律, 波长位于气体吸收线附近的光能量被气体分子吸收, 导致透射光强度减弱。通过光电探测器探测光强的变化, 可反演得到待测气体的浓度信息[8,10]。可调谐二极管激光吸收光谱技术主要包括直接吸收光谱与波长调制光谱两种技术类型。在波长调制光谱技术中, 激光器的驱动信号中叠加了调制作用的高频正弦信号, 利用锁相放大技术提取出二次谐波信号, 降低了随机噪声的影响。波长调制光谱技术的原理如图1b所示。

图1 基于波长调制光谱的红外气体传感系统的信息传递模型与检测原理Fig.1 Information transmission model and detection principle of infrared gas sensing system based on wavelength modulation spectroscopy
激光器的驱动信号由起扫描作用的三角波和起调制作用的高频正弦波叠加形成, 激光器的驱动电流为
i(t)=i0+ibcos(wt)
(1)
其中i0为激光器的偏置电流,ib为电流调制幅度,w为调制信号的角频率。输出激光的波数与光强分别为
v(t)=v0+vmcos(wt)
(2)
I0(t)=I0+ηI0cos(wt)
(3)
其中v0为光源的中心频率,vm为频率调制幅度,I0为初始光强,η为光强调制系数。透射光I与入射光I0满足朗伯-比尔定律
I(v)=I0(v)exp[-α(v)CL]
(4)
其中α(v)为吸收系数,L为吸收光程,C为待测气体浓度。在弱吸收条件下, 满足α(v)CL≪1, 则式(4)可近似为
I(v)=I0(v)[1-α(v)CL]
(5)
将α(v)进行傅里叶展开, 得到
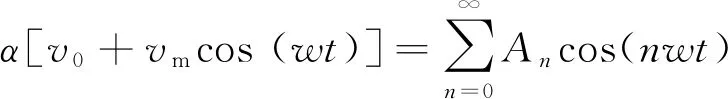
(6)
其中An为吸收系数的n级傅里叶级数的系数, 当vm较小时,An正比于α(v)的n阶导数, 且n次谐波信号的幅值Sn如下[10]
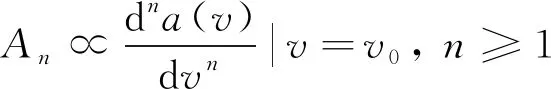
(7)
Sn∝I0CLAn
(8)
可见,Sn正比于初始光强、 气体浓度、 吸收光程和吸收系数的n级傅里叶级数的系数。因此, 只要测得n次谐波的幅值, 根据标定关系可得到气体浓度。在实际应用中一般使用二次谐波信号表征气体浓度[10-15]。
使用Matlab软件对上述基于波长调制光谱的气体检测过程进行仿真。选取位于3 291 nm处的甲烷吸收线, 设置甲烷浓度为100×10-6。扫描信号----三角波的频率为5 Hz, 调制信号----正弦波的频率为5 000 Hz。仿真得到的透射光强I的波形如图2a所示。在吸收波长处, 由于激光光强被气体分子吸收, 信号出现了凹陷。将该信号分别与频率为10 000 Hz的同相和正交信号相乘, 再进行低通滤波, 得到同相分量(I)与正交分量(Q)。由于低通滤波的信号可能为负, 因此, 在两分量中加入固定的偏置保证信号为正值, 将这两个信号平方相加后开方, 从而消除相位差的影响。实际测得的信号波形如图2b所示。进行基线拟合后(见图2c), 得到了幅值正比于气体浓度的二次谐波信号, 如图2d所示。

图2 波长调制光谱技术的仿真结果Fig.2 Simulation results of wavelength modulation absorption spectroscopy technique
2 传感信息度量方法
2.1 转移矩阵
根据图1a, 测量气体浓度过程是一个传递信息过程。假设待测气体浓度是已知的、 确定的值, 但在测量中, 由于噪声影响, 实际测得浓度值会分布在一个特定的范围内, 如果测量几个比较接近的真值, 实际测得的几组浓度值可能会发生交叠。此时, 对一个特定的测量值, 不能确定这个测量值对应的真值。与精确的浓度信息相比, 得到的浓度信息比较模糊, 即在这个过程中存在信息的损失。因此, 需要建立一种传感信息度量方法, 可定量描述测量过程中信息的损失及其对测量浓度的影响。根据香农信息论, 即使测得气体浓度, 获得一部分关于实际气体浓度的信息量, 但对实际气体浓度X仍然存在不确定性。此时, 通过传感系统的转移矩阵可描述信息传输与损失情况[1], 进而使用传感系统的信息传递效率和最小可分辨浓度间隔可评估传感系统的信息传输有效性。
将发送信源(气体的真实浓度)用随机变量X表示, 其取值为{x1,x2,…,xn},n为浓度的取值个数。通过传感系统处理后, 输出变量(测量的气体浓度)为Y, 取值为{y1,y2,…,yr}。如果没有噪声,X与Y存在确定的对应关系, 如测量x1, 接收端必然接收到y1。考虑传感系统的噪声, 发送某个x时, 传感器输出的y不是确定值。该过程采用转移概率描述, 即
P(y|x)=P(y=yb|x=xa),b=1,2,…,r;a=1,2,…,n
(9)
式(9)给出了当实际的气体浓度为xa时, 传感器输出浓度为yb的概率。考虑所有实际浓度与测量浓度的情况, 可将传感器的转移特性写为矩阵形式, 如表1所示。
转移矩阵描述了实际浓度与测量浓度之间的转移关系, 可进一步使用平均互信息描述通信后得到的信息量。信源X的信息量与Y的信息量可分别表示为
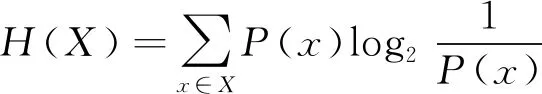
(10)

(11)

表1 转移矩阵
通过传感器输出浓度Y获得的关于实际浓度X的信息量称为互信息量, 计算式如下
I(X;Y)=H(X)+H(Y)-H(XY)
(12)
其中H(XY)为X、Y的联合信息量, 可由
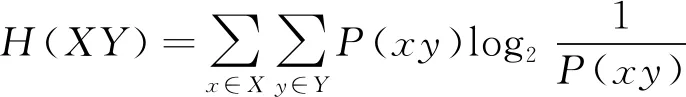
(13)
计算。其中P(xy)=P(x)P(y|x)为联合概率密度。
2.2 传感系统的信息传递效率和最小可分辨浓度间隔
转移矩阵建立了实际浓度与测量浓度的相互关系, 由转移矩阵和式(12)可计算传感系统输出的信息量[4,9]。在度量红外气体检测系统的检测精度时, 可将传感器等效为离散有噪信道, 其输入是一组离散气体浓度值, 如100×10-6、110×10-6、120×10-6。受噪声影响, 当设定浓度为100×10-6时, 测得的浓度可能偏离实际值, 从而造成了混淆。假设待测的气体具有多个浓度值, 将测得的浓度值量化后划分至指定区间, 用区间频率代替概率, 可计算出转移概率。将每个浓度区间的转移概率写成矩阵的形式, 可得转移矩阵, 再结合式(10)~式(13)可定量计算信息量的损失。
为衡量在一定浓度范围内测量浓度的混淆程度, 可选择多组等概率的气体样品作为输入信源X的符号集。在实际应用中, 可依次配置这些浓度的气体样品, 各样品间互不干扰, 因此可认为选择每个气体浓度的概率相等, 此时可得H(X)=-log2(1/n), 其中n为待测气体样品个数。
计算互信息时, 首先确定输入变量X与输出变量Y可能的取值, 输入变量取值为设置的浓度。针对输出变量, 首先, 确定测得浓度的最大值与最小值; 其次, 对采集到的数据进行量化和分组, 统计各组的频次, 计算出转移概率P(y|x); 然后, 计算Y的概率分布P(y)和H(Y); 最后, 计算XY的联合概率分布P(xy)和联合熵H(XY), 最终计算得到互信息量I(X;Y)。
定义红外气体传感器的信息传递效率η, 用于衡量系统传输信息的能力,η越大, 说明系统传输传感信息的能力越强, 受到的干扰越小。即有

(14)

图3 当实际浓度X={100,101,102,103,104,105}×10-6时, 模拟得到的传感器测量浓度的分布Fig.3 Under the case of practical concentrationinformation source X={100,101,102,103,104,105}×10-6,the simulated distribution of the measured concentration
作为示例, 选取6个等间隔的浓度点{100,101,102,103,104,105}×10-6作为传感器的输入信源X, 此时n=6, 浓度间隔Δx=1×10-6。通过模拟方法, 随机生成了间隔为1×10-6、 标准差为0.5×10-6的6组浓度数据, 每个浓度点下生成10 000个浓度值。对各组浓度数据进行高斯拟合, 得到各个浓度测量值的归一化频数曲线, 如图3所示。输出浓度的取值范围为(98~107)×10-6。由于将传感器等效为离散有噪信道, 将连续的归一化频数曲线离散化, 得到一组用于构建转移矩阵的离散浓度点。令离散化的浓度间隔为Δy=0.1×10-6, 将离散化区间内的频数累加作为该区间浓度点的频数, 比如[100×10-6,100.1×10-6]区间, 统一使用区间左端点(100×10-6)作为区间浓度以及累加后的频数值作为区间频率。根据图3概率分布, 计算离散化后各区间的概率分布, 从而得到传感器的输出信源Y。发送信源的熵H(X)=-1/6log2(1/6)=2.585(bit/符号), 接收信源的熵H(Y)=6.081(bit/符号), 联合熵H(XY)=6.952(bit/符号), 平均互信息I(X;Y)=H(X)+H(Y)-H(XY)=1.714(bit/符号), 对应的信息传递效率η=66.4%。
在保持输入浓度间隔不变的前提下(即保持Δx=1×10-6), 通过改变测量浓度的标准差(定义为σ, 代表传感系统的噪声水平)与浓度间隔(表明传感系统区分浓度的能力)的比值研究接收端获得的互信息与信息传递效率的变化, 二者可分别通过式(12)、 式(14)计算得到。如图4a所示, 随着σ/Δx的增大,I(X;Y)与η逐渐降低, 这是由于当Δx不变时, 随着σ的增大, 不同组中的测量数据的重叠程度增大, 使测量浓度之间变得更难以区分, 即信息量降低。在一定的噪声水平下(即σ一定时), 当互信息量达到输入信息量即η=100%时, 定义相应的浓度间隔为传感器的最小可分辨浓度间隔Δxmin。根据图4, 计算得到传感系统的最小可分辨间隔为Δxmin=2.8×10-6。其中X={100,101,102,103,104,105}×10-6。

图4 信息传递效率、 互信息量随标准差与浓度间隔比值的变化曲线Fig.4 Curve of information transmission efficiency and mutual information versus the ratio between the standard deviation and concentration interval
3 传感系统的信息传递效率分析
为评估实际的红外气体传感系统的信息传递效率, 选择吸收较强的中红外3 038.5 cm-1的甲烷吸收线作为目标吸收线, 建立了基于波长调制光谱技术的中红外甲烷检测系统。使用中心发射波长为3 291 nm的带间级联激光器, 气室的光程为26 m, 采用热电制冷红外探测器探测红外光信号。通过测量氮气背景下的系统输出浓度评估系统的噪声水平。
图5a给出了对系统背景噪声进行长时间测量得到的甲烷浓度值, 测量时间为2 000 s, 标准差σ=0.15×10-6。图5b给出了测量浓度的频数分布直方图与概率分布的拟合曲线。可以看出, 测量的浓度数据近似服从高斯分布。利用图5a得到的浓度分布, 将发送信源X的浓度个数设置为6组, 浓度间隔设置为Δx=0.1×10-6。
传感器实际测得的浓度(接收信源Y)分布如图5c所示。图5d给出了系统艾伦标准差随积分时间的变化曲线。当积分时间为1 s时, 艾伦标准差为0.15×10-6(等于标准差)。随着积分时间的增加, 艾伦标准差逐渐下降, 系统的稳定性随之增强。当积分时间为200 s时, 艾伦标准差达到0.02×10-6。
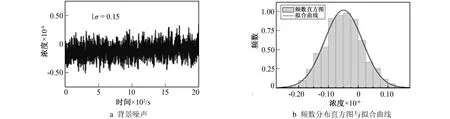

图5 在氮气环境下, 对传感器背景浓度数据的测量、 分布和艾伦标准差分析Fig.5 Measurement results, distribution and Allan deviation analysis on background concentration of the sensor system in N2 atmosphere
通过改变浓度间隔Δx, 探究了Δx对传感器的互信息和信息传递效率的影响, 如图6a,图6b所示。随着Δx的增大, 互信息量增加, 当Δx足够大时, 互信息等于信源的信息熵, 此时信息传递效率为100%。当积分时间分别为1 s、5 s、10 s、20 s、100 s和200 s时, 最小可分辨的浓度间隔分别为0.83×10-6、0.78×10-6、0.56×10-6、0.44×10-6、0.22×10-6和0.11×10-6。图6c为最小可分辨浓度间隔随积分时间的变化曲线。随着积分时间的增加, 最小可分辨浓度间隔逐渐减小, 对应的噪声水平随之降低, 系统稳定性提高。

图6 不同积分时间下, 对传感器互信息、 信息传递效率和最小可分辨浓度间隔的分析Fig.6 Analysis of mutual information, information transmission efficiency and the minimum resolvable concentration interval of the sensor system
4 结 语
笔者针对“信息论”课程的教学需求、 波长调制光谱技术的噪声分析与传感系统的长时间工作稳定性评估的需要, 首先建立了红外气体传感系统的信息传输模型以及波长调制光谱技术的理论模型, 使用Matlab软件对波长调制光谱技术进行了仿真。结合“信息论”中相关理论, 给出了转移矩阵、 信源熵、 互信息等数学表达式, 分析了气体传感系统的信息传递效率、 最小可分辨浓度间隔等特性。利用传感器长时间稳定性的实际测量结果, 分析了传感系统的信息传递效率、 最小可分辨浓度间隔随系统积分时间的变化特性。本文给出的红外气体传感系统的信息度量方法满足“信息论”课程的教学需求以及波长调制光谱技术的科研需要, 取得了较好的教学与科研效果。

