多阶阻抗匹配与宽频带天线的设计分析

王 乐，赵志鹏，李亚楠，刘金海，尹应增，李 晖

(西安电子科技大学 天线与微波技术重点实验室，陕西 西安 710071)

随着技术的发展，天线在军事、医疗、航天等各个领域都起着重要的、不可替代的作用，但对天线的要求也日益苛刻．宽频带是天线领域长久不衰的重点研究方向．宽频带天线不仅可以有效地减少天线的数量，还可以降低元件间的互相干扰．常见的展宽频带技术有机电结合、阻抗加载技术和匹配网络技术等．文献[1]对RC负载用电容电感组成的五阶切比雪夫网络进行匹配，使相对阻抗带宽达到10%; 文献[2]中，通过引入一对 1/4 波长的微带线谐振器，进行二阶阻抗匹配，使得工作在 4.9 GHz 频点的微带贴片天线的带宽比传统的微带贴片的带宽宽2.7倍; 文献[3]中将插入型的梯形微带天线的馈线进行平移以及 1/4 波长的阻抗变换，对天线进行二阶阻抗匹配，使其相对阻抗带宽增加了276%．

笔者从阻抗匹配方程出发，对阻抗匹配原理进行了系统性总结．通过分析阻抗匹配方程，阐述了一阶匹配和二阶匹配的关系，并且通过Matlab软件画出天线多阶阻抗匹配相对带宽的极限图．多阶阻抗匹配技术是展宽天线的阻抗带宽的主要方法．多阶阻抗匹配的主要方法是在辐射体或者馈电网络上进行匹配，通过增加匹配网络的阶数来增加谐振点，从而拓宽阻抗带宽．最后，结合几个实例，对阻抗匹配进行了分析．

1 基本理论分析

天线的输入阻抗可以等效为电阻R、电感L和电容C的串联或者并联[4-5]，图1所示的是串联形式．当天线谐振时，其阻抗可以等效为电阻R，属于一阶阻抗匹配，通过理想阻抗变换器对天线进行最优匹配;当天线谐振频率偏低时，由天线的等效电阻R、电感L和电容C串联而成的天线输入阻抗呈现容性，需要加感性元件使其匹配;当天线谐振频率偏高时，其输入阻抗呈现感性，需要加容性元件使其匹配．而天线的相对阻抗带宽B可以用它们的品质因数Q(电抗与辐射电阻的比值)来表征．对于基本的电容、电感、电阻串联的电路，相对阻抗带宽B被认为与品质因数Q成反比[6-8]，而品质因数Q通常为平均储存能量与损失能量之比的2π倍．品质因数Q值越大，说明辐射的能量越小，相对阻抗带宽B就越小．

文献[9]根据图1所示的理想匹配等效电路图，提出了阻抗匹配方程:

(1)

其中,B为理论上最大的相对阻抗带宽，Q为天线的品质因数，Γ为天线的反射系数，ω0为天线的谐振角频率．因为是理想阻抗变换，所以得到的是最大的阻抗带宽．

图1 天线理想阻抗匹配等效电路图图2 多阶阻抗匹配等效电路图

多阶阻抗匹配是通过电感L和电容C的交替并联和串联组成的一个n阶谐振电路，谐振频率为中心频率，如图2所示．文献[10]使用网络理论方法，推导出阻抗匹配阶数从1到∞的品质因数Q、n阶匹配相对带宽Bn与反射系数Γ的关系(n是多阶阻抗匹配网络中的匹配阶数):

其中，a，b是方程组的系数．这3个方程联立可以解出任意阶阻抗匹配的相对带宽．当阻抗匹配的阶数n趋于无穷大时，文献[9-10]的阻抗匹配方程一致:

(5)

其中，B∞是无穷阶阻抗匹配时的相对阻抗带宽．

同时，文献[11]从另一个角度阐述了阻抗匹配方程，但是仅适用于阻抗匹配阶数为1和2的情况．当天线等效为电阻R、电感L和电容C串联的电路时，文献[11]中的3个方程准确地表达了其相对阻抗带宽与反射系数的关系：

其中，φEB是边频带的阻抗相位，Γ1为一阶匹配的反射系数，Γ2为二阶匹配的反射系数．

方程(6)～(8)是以天线等效的R、L、C串联电路为基础，并且天线谐振在中心频率上，即电感L和电容C在中心频率谐振．等效的R、L、C值是与频率无关的常量，因此使用ADS软件对等效的R、L、C串联电路进行仿真，电路图如图3所示．天线的输入阻抗等效的R、L、C串联电路中，L=L1= 1.381 nH，C=C1= 0.401 pF，R= 50 Ω，此时为一阶匹配; 用并联的电感L2和电容C2对天线进行二阶匹配，L2= 0.983 61 nH，C2= 0.561 4 pF．对电路进行仿真分析，得出的结果以史密斯圆图来呈现，用以说明一阶和二阶匹配的关系．

图3 天线等效电路ADS仿真图图4 一阶与二阶匹配史密斯圆图

如图4所示，fL和fH是天线的低频和高频．对天线进行一阶匹配时，使得中心频率到达原点，获得最优匹配，但是这只匹配了一个频点，而需要的是在fL～fH整个频段内都能达到反射系数Γ2之内．因此，需要进行多阶匹配．首先将天线等效的阻抗R减小，使中心频率点的反射系数处于Γ2的边缘．此时整个频段的反射系数都会平移，处在Γ1圆里．然后通过阻抗匹配增加寄生单元，相当于引入了并联的LC等效电路，如图4的二阶匹配，天线会增加一个谐振点，使低频和高频的反射系数都向Γ2圆靠拢，阻抗匹配特性更加良好，并且频带内所有的反射系数都在Γ2圆内，达到二阶最优匹配，在fL～fH频段内都能达到相应的反射系数Γ2以内．这就是一阶阻抗匹配到二阶阻抗匹配的变换过程．

文献[10]根据阻抗匹配方程(6)～(8)，推导出多阶阻抗匹配方程:

式(11)对于n=1，2是准确的，并且对于Γ>1/3提供了n从3到∞的良好近似，这是最初的阻抗匹配方程．关于系数an的确定，结合文献[9-10]的阻抗匹配方程，对于Γ> 1/3，a1=1，a2=2，a∞=π，用无穷级数[12]去近似系数an，如式(12)．给式(12)扩大两倍，则得到另一个无穷级数，如式(13)．该无穷级数的第1项和及第2项和分别为1和2，并且该无穷级数求和为π，与系数an相对应．所以该无穷级数的其他项和分别对应an的其他项，如式(14)．

用无穷级数确定的系数an，使得式(11)与文献[10]的阻抗匹配方程相比较有一点细微的误差．为了阻抗匹配方程更加精确，在式(11)的基础上，引入了系数bn，并且对系数an和bn进行了修正，如表1所示．改进后的多阶阻抗匹配方程为

(15)

其中，系数bn用于从 1/ sinh[ln(1/Γ)/an]函数转换到an/ ln(1/Γ) 函数．使用MATHCAD软件来求解文献[10]的阻抗匹配方程，并精确地确定n从3至8的an，使得对于Γ= 0.99，Bn的误差接近于零． 然后确定n从3至8的参数bn，使得对于Γ= 0.1，Bn的误差接近于零．与文献[10]阻抗匹配方程相比，相对阻抗带宽Bn的求解更加方便，而且精度与文献[10]的阻抗匹配方程基本一致．

表1 系数an 和bn

根据阻抗匹配式(15)，通过Matlab编程，将相对阻抗带宽与n阶匹配的关系展现出来，如图5所示．

由图5可知，当反射系数Γ=1/3时，随着阻抗匹配阶数的增加，1/(QB)的值逐渐减小，所以阻抗带宽B逐渐增加，但是阻抗带宽增加的趋势越来越平缓; 当阻抗匹配阶数n为∞时，阻抗带宽趋于定值，而非无穷大．以Γ= 1/3 为例，B2/B1= 2.31，增加131%;B3/B2= 1.24，增加24%;B4/B3= 1.10，增加10%．因此，理论上可以通过增加阻抗匹配的阶数来提高天线阻抗带宽．

图5 n阶阻抗带宽与反射系数的关系图6 G形单极子示意图

2 实例分析

2.1 宽带G形单极子

普通的单极子经过弯折变形，变成G形单极子天线[13]，如图6所示．将直立的单极子弯折成开口的矩形环，通过在馈电端口引入小方环做阻抗匹配．开口矩形环的3个臂长L1、L2和L3分别为 70 mm、75 mm 和 75 mm，小方环的臂长L4为 35 mm，整体的高度H为 107 mm (0.41λ)．

利用高频结构仿真(High Frequency Structure Simulation，HFSS)电磁仿真软件对天线进行仿真分析，结果如图7所示．当该G形单极子没有引入小方环时，在 0.8～ 1.5 GHz 谐振频率内，天线的输入阻抗实部约为 100 Ω，并且天线的输入阻抗虚部随频率变化很大，此时它处于自身的谐振中，匹配效果不理想．而当该G形单极子引入小方环时，可以看出，在谐振频率内，天线的输入阻抗实部约为 50 Ω，而且天线的输入阻抗虚部随频率变化很小，基本都在0附近变化，阻抗匹配效果良好．小方环的作用就是对天线进行二阶阻抗匹配，使天线的阻抗随频率变化更小一点，匹配效果更佳．因此，将小方环加载在该单极子天线的底部，可以进行良好的阻抗匹配，增加阻抗带宽．如图8所示，当驻波比小于2时，没有引入小方环的单极子阻抗带宽为 0.98～ 1.08 GHz，相对带宽为9.70%; 引入小方环后的单极子阻抗带宽为 0.93～ 1.48 GHz，相对带宽为46.80%，表明多阶阻抗匹配能够有效地增加带宽．

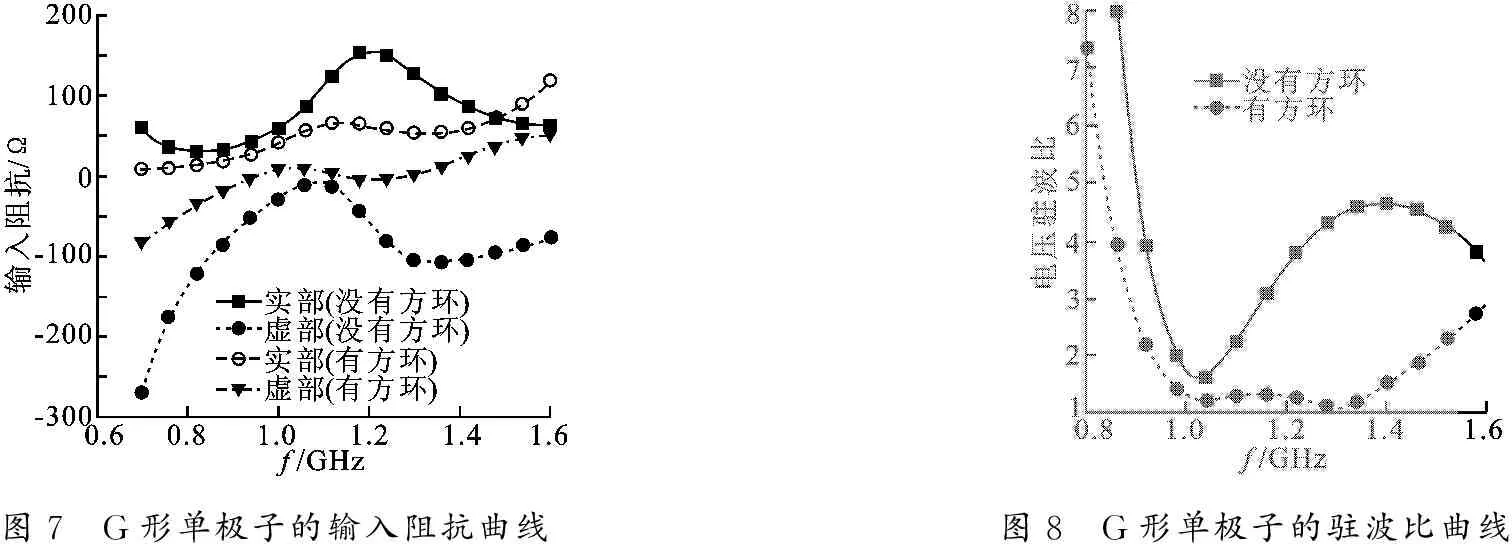
图7 G形单极子的输入阻抗曲线图8 G形单极子的驻波比曲线

2.2 三阶匹配宽带单极子

对于单极子天线来说，直接加粗振子可以得到较低的特性阻抗，不过效果不太显著，可以通过其他方式来改善单极子的阻抗特性．天线结构[14]如图9所示，在单极子天线的外面加上一个与之同轴的金属套筒，就形成了套筒天线．加上的金属套筒就相当于一个加粗的振子，它的馈电方式特殊，相比较普通的振子天线，这种天线的阻抗特性更好．除了单极子本身谐振外，套筒也参与了谐振，形成了二阶匹配，使得阻抗带宽从 370～ 452 MHz (相对阻抗带宽约为20.05%)展宽到 399.50～ 688.76 MHz (相对阻抗带宽约为55.14%)，相对阻抗带宽增加了175.00%，如图10所示．在二阶匹配的基础上，再增加一阶阻抗匹配，即在金属圆筒外面加上4个金属柱，金属柱与地相接，构成了开式套筒．这4根寄生振子起到了加粗单极子的作用．此时天线有3个谐振点: 一个是单极子自身的谐振点，另一个是套筒激励的谐振点，最后一个是4根寄生振子引起的谐振点．这3个谐振点彼此靠近，将天线的阻抗带宽拓宽．天线的阻抗带宽增加到了 377.65～ 840.20 MHz，相对阻抗带宽约为82.11%，相比较二阶阻抗匹配，相对阻抗带宽约增加了48.89%．

图9 三阶匹配宽带单极子的模型图图10 三阶匹配宽带单极子驻波比曲线

3 结 束 语

天线的输入阻抗等效于电阻R、电感L和电容C的串联谐振电路．对天线进行多阶阻抗匹配，匹配可以做在辐射体上，也可以做在馈电网络上，可以有效地展宽阻抗带宽．基于文献[9-13]的阻抗匹配理论，随着阻抗匹配阶数的增加，阻抗带宽不断地增加，但天线无穷阶阻抗匹配的带宽在理论上是有限的．笔者给出了两个实例验证了多阶阻抗匹配的有效性：弯折单极子通过引入阻抗匹配环来实现二阶的阻抗匹配，其相对带宽从9.70%增加到46.80%; 套筒单极子天线通过引入4根匹配金属柱来实现三阶的阻抗匹配，其相对阻抗带宽从55.14%展宽到82.11%．