各向异性大气湍流中涡旋Lommel光束传输特性
杨瑞科,周 静
(西安电子科技大学 物理与光电工程学院,陕西 西安 710071)
近年来基于光子轨道角动量(Orbital Angular Momentum,OAM)的自由空间光通信(Free Space Optics communication,FSO)备受关注,因为它可以在不增加光谱带宽的前提下显著提高信道的信息容量[1].理论上轨道角动量数(或称拓扑荷)l为任意整数,可以构成无穷维希尔伯特空间,因此,较传统的二进制编码,光束的轨道角动量编码能够有效地提高数据传输容量[2].且基于轨道角动量光通信的轨道角动量间的串扰小,与传统的二维量子密钥分发方案相比,它的量子高维密钥分发方案具有更高的防窃听特性[3-4].
大气湍流是限制FSO通信发展的关键因素之一[5],因此,涡旋光束在大气湍流中传输特性研究对减缓湍流效应措施具有重要意义.自1992年,文献[5]发现带有相位因子 exp(imθ) 的光束中每个光子具有hm/(2π) 的轨道角动量后,携带轨道角动量的涡旋光束及其传输特性研究得到极大的关注[6].文献[7]研究了在FSO光链路由湍流引起的信道串扰的轨道角动量复用.文献[8]利用Rytov近似,分析了湍流对拉盖尔-高斯谢尔(Laguerre-Gaussian Schell)光束的模式概率、串扰概率的影响.文献[9]计算了多汉克-贝塞尔(Multiple Hankel-Bessel,MHB)光束在各向异性大气湍流中的传输特性,分析了各向异性湍流参数对叠加的轨道角动量模式概率的影响.然而,对无衍射的涡旋光束在各向异性大气湍流中传输特性的研究并不多.
无衍射洛默尔(Lommel)光束是一种携带轨道角动量的光束,其实质是贝塞尔模式的无穷线性叠加,其波矢量具有相同的轴向投影,它是最近发展起来的一种傍轴无衍射光束[10],具有很窄的光束半径,中心光斑半径可以非常窄,且不受传播距离而改变.近年来,无衍射涡旋光束已可用于FSO通信的光束源,可作为减缓大气湍流效应的一种有效措施[11].对无衍射MHB涡旋光束的研究表明,其在大气湍流中的传输性能优于经典的拉盖尔高斯光束[9].因为无衍射光束的横向强度分布在传播过程中被结构化地保持,遇到障碍物后能够重构,这有助于减轻湍流的不利影响[12].
迄今,关于Lommel光束在各向异性非科尔莫戈罗夫(non-Kolmogorov)大气湍流中传输特性的研究还鲜有报道.文中对具有不同轨道角动量和波束参数的Lommel光束在不同程度各向异性non-Kolmogorov湍流(即湍流谱幂指数,广义折射率结构常数,湍流内、外尺度等参量变化)中传输时的各个轨道角动量模的接收功率和不同轨道角动量模之间的串扰功率进行理论推导和数值分析研究.该研究可为自由空间涡旋光束通信及减缓湍流效应措施的进一步研究提供参考依据.
1 理论分析
无衍射Lommel光束在柱坐标系下的电场解析表达式为[12]
(1)
其中,r=|r|,r=(x,y),是源平面内的位置矢量;φ是方位角;z为传播距离; 波数k= 2π/λ,λ是波长; 而kρ是波数的横向分量; Jl0+2p表示第一类贝塞尔函数;c是不对称复数参数; 整数l0是光子轨道角动量数(也称为拓扑荷数).为了分析Lommel涡旋光束的特性,在图1中给出了Lommel光束在源平面 (z=0) 处横向强度分布,其中光束的各项参数为l0=1,λ= 1 550 nm,kρ= 0.001k,在柱坐标下,x,y的取值范围是 -0.01 m≤x,y≤ 0.01 m.图1显示出,当c值较小时,Lommel光束的衍射图案接近于圆对称.随着不对称参数c的增加,圆对称现象消失,在横平面上形成的强度图具有轴对称形状的两个新月牙分布[13].可看出对称轴的方向由参数c决定.

图1 源平面上不同c值的Lommel光束的横向强度分布图
在大气湍流中,携带轨道角动量的Lommel光束的复振幅在柱坐标系(r,φ,z)下的表达式为
E(r,φ,z)=Eo(r,φ,z) exp[ψ(r,φ,z)] .
(2)
大气湍流的折射率起伏对在其中传播的光场有干扰作用,从而使得轨道角动量模并不能保持其原有的量子态,而是在湍流作用下跃迁到相邻的轨道角动量模上,形成串音干扰[3].因此,接收处的光波可以改写为携带相位因子 exp(ilφ) 的螺旋谐波的叠加模式[14],即
(3)
而展开系数βl(r,z)为
(4)
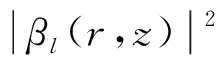

(6)
其中,ρ0是球面波在各向异性的non-Kolmogorov湍流下的空间相干长度,形式为
(7)
其中,φn(κ)是各向异性大气湍流的功率谱.假设湍流各向异性只存在于光束的传播方向上,并考虑湍流内、外尺度的影响,采用各向异性non-Kolmogorov湍流谱[9],即
(8)

A(α)=Γ(α-1) cos(πα/2)/(4π2);c(α)={πA(α) Γ(3/2-α/2) [(3-α)/3]}1/(α-5),
(9)
其中,Γ(·)是伽马函数.利用马尔科夫近似,忽略式(9)中空间波数κz分量,再将式(8)代入式(7)中,得到[9]
(10)


(11)
其中,I(·)表示功率.可得到各向异性湍流下的Lommel光束模式概率的表达式为
其中,Jl0+2p和Il-l0-2p分别表示第一类贝塞尔函数和第一类修正贝塞尔函数,ρ0是式(10)表示的各向异性湍流中的Lommel光束的相干长度.

(13)
其中,D是探测器孔径直径.轨道角动量模的接收功率Pl0表示在接收平面处接收信号的拓扑电荷为l0的归一化功率(即当l=l0时的功率),即在接收平面处探测到的轨道角动量模l等于Lommel光束在发射平面处携带的轨道角动量模l0.Pl为轨道角动量的串扰功率,即在接收平面处接收信号的拓扑电荷为l=l0+ Δl的归一化功率.
2 计算分析
根据Lommel涡旋光束携带轨道角动量模为l归一化功率公式(13),在波束和湍流参数为λ= 1 550 nm,D= 0.05,c=0.1,α=3.37;L0=50 m;ls= 1 mm;z= 2 km 时,主要计算分析各个光束参数和湍流条件对不同模式轨道角动量信号的接收功率和串扰功率的影响.这里及以下所指功率均是归一化功率.


图2 不同OAM模的Lommel光束在湍流中传输时的接收功率

图3 湍流各向异性对Lommel光束传输时接收功率和串扰功率的影响

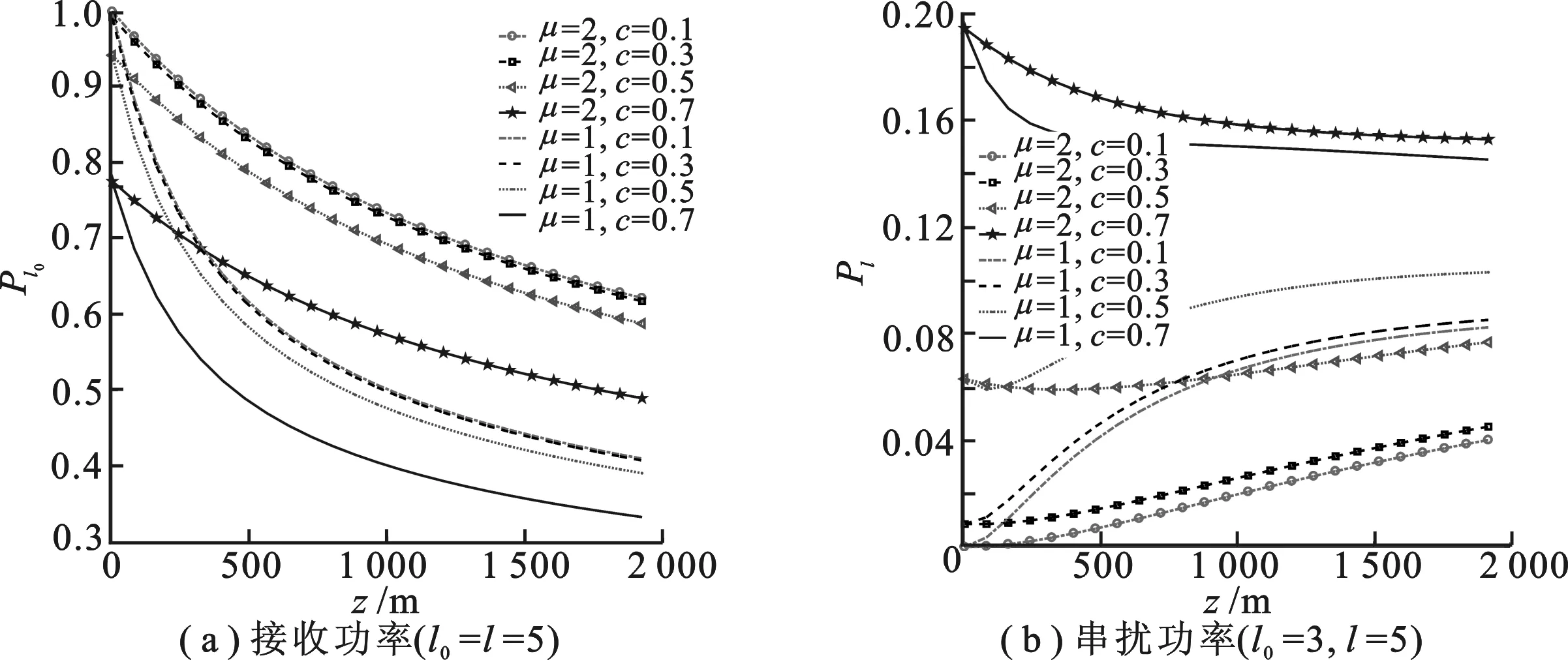
图4 Lommel光束的不对称参数值c对接收功率和串扰功率的影响
从图4可看出,不对称参数c的值越大,轨道角动量模的接收功率就越小,而且串扰概率也越大.当c的值小于0.3时,结果较接近,当c= 0.7时,结果相差的就比较大.因为c是影响Lommel光束横向强度分布的一个关键因素.当c值较小时,光束强度分布接近于圆对称.随着c的增加,光束强度分布逐渐偏离圆对称.这表明近于圆对称模式下的Lommel光束能更好地减轻湍流的影响.且可发现,Lommel光束在各向异性的大气湍流中的传输性能明显优于在各向同性湍流中的性能.

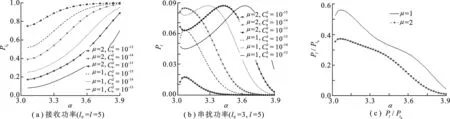
图5 不同湍流强度和谱参数时Lommel光束的接收功率和串扰功率
3 结 束 语
分析了携带轨道角动量的非衍射Lommel光束在各向异性的大气湍流中传播时,湍流以及光束的一些参数对轨道角动量模的接收功率和串扰功率的影响.不仅考虑了轨道角动量数、湍流强度、幂指数参数α和湍流的各向异性系数的影响,还分析了Lommel光束的不对称参数对传输性能的影响.研究表明,湍流各向异性的系数越大,光束的轨道角动量模的接收功率越大,其串扰概率越小.即对不同强度的湍流,各向异性大气湍流中的接收功率要高于各向同性的结果.另外,轨道角动量等于5时,接收功率稍大些,还有在弱湍流中,轨道角动量数是奇数时的接收功率稍高于偶数时的情况.对于不同湍流强度的non-Kolmogorov幂指数参数α的变化对接收功率和串扰功率都会有较大的影响.对于不同形状的Lommel波束,越接近于圆对称模式时,越能更好地减缓湍流的影响.所以,为了获得较高的接收功率以及较小的串扰功率,应该选择不对称参数值较小的Lommel光束.

