基于认知风险动态平衡的智能汽车跟车模型*
刘巧斌,杨 路,高博麟,王建强,李克强
(清华大学车辆与运载学院,汽车安全与节能国家重点实验室,北京 100084)
前言
跟车行为是最基本的驾驶行为之一,深入研究驾驶人跟车行为和跟车建模方法不仅对开发自适应巡航系统等高级驾驶辅助系统至关重要,也是智能汽车实现自动驾驶必须着力攻克的重要课题[1]。
驾驶人跟车行为受到驾驶技能、驾驶风格、车辆动力学性能、行驶路况和周车状况等众多复杂因素的影响,且由于驾驶人心理、性别、年龄和疲劳程度的不同,使得驾驶人跟车行为存在一定的随机性[2]。此外,跟车对的车型不同,造成前后车动力学性能有所不同,驾驶人对行车风险的主观认知将产生变化,引起跟车行为的异质性[3-5]。最后,跟车过程中,驾驶人对风险和效率的敏感程度存在差异,加速时希望平稳加速,而减速时倾向于较大的制动强度和高灵敏的减速度响应,以维持客观的安全和主观心理上认知到的风险保持在可接受的阈值区间内,以上驾驶心理造成驾驶人跟车过程中加减速强度的非对称性[6]。
为解决跟车过程中随机性、异质性和非对称性造成的跟车建模难题,在日趋准确和丰富的自然驾驶行车轨迹数据集的驱动下,相关研究不断深入,使得模型的准确度和建模的效率都得到较大的提升[7-8]。现有的跟车模型可分为机理模型和数据驱动模型。典型的机理模型有刺激-反应模型[1]、优化速度模型[9]、安全距离模型[10-12]和社会力模型[13-14]等,这些模型通过建立运动学参数之间的数学关系对跟车行为进行描述。数据驱动模型通过人工智能方法,如神经网络[15-16]、深度学习[17]和强化学习[18]等方法实现对跟车行为的预测。数据驱动的跟车模型虽然在拟合精度上有一定的优势,但存在可解释性差和泛化能力不足的局限[19-20],因此,拓展并完善可解释可泛化的机理模型仍为跟车建模领域的重要方向之一。
为提升异质车型影响下复杂交通环境的智能汽车决策性能,有必要借鉴驾驶人跟车决策的智慧,开展智能汽车拟人化的跟车决策研究。深入探索异质性和非对称性的驾驶人跟车行为,探明驾驶人跟车行为随机性的原因,为提升智能汽车跟车决策的科学性和合理性提供参考,以减小不确定性行为可能造成的跟车风险的增加、跟车舒适性的降低和行车效率的下降等问题。此外,现有不同数学形式的跟车模型仍有待在机理层面进行统一的解释。有鉴于此,本文从认知风险动态平衡的角度出发,旨在获取驾驶人跟车模型的一般化数学表达,为智能汽车的拟人化跟车决策提供基础。以公开的自然驾驶数据集HighD为基础,从异质跟车对的跟车行为分析出发,探索跟车过程中跟车距离的变化规律,发现稳态跟车工况下车头时距和逆碰撞时间“两不变”的规律;同时对不同货车-轿车组合下的跟车对的加速度响应平衡线进行辨识,结合认知风险理论,建立认知风险与加速度响应的映射关系,实现对复杂交通环境下跟车加速度的客观量化预测。
与传统跟车模型相比,本文所提出的模型创新性主要体现在两个层面。在理论层面,所提出的驾驶人通过纵向加速度维持认知风险的动态平衡的假说,将不同跟车模型统一在同一数学表达式框架下,常用的IDM、GM和LCM跟车模型都可视为本文模型的特例。在技术层面,给出了一种可行的线性化认知风险平衡线,在此基础上,提出一种简洁的加速度响应模型,它能够充分考虑动态交通环境中车型的异质性和驾驶人加减速响应的非对称性,且具备更好的拟人性。
首先,对自然驾驶跟车数据的规律进行分析,从中总结出“两不变”规律,并采用作图法获得加速度响应的平衡线;其次,对现有跟车模型进行类比分析,揭示“两不变”参数的物理意义,在此基础上,提出一种简洁的非线性函数用于表述认知风险动态平衡的跟车模型,根据实测数据对模型的准确性进行验证;最后,对全文研究工作进行总结,并对下一步的研究进行展望。
1 自然驾驶跟车行为的“两不变”规律
在自然驾驶跟车过程中,驾驶人跟随前车以一定的速度和车距行驶,随着前车车速的变化,自车通过加速踏板和制动踏板调整与前车的安全车距和自车车速。跟车过程中涉及到的关键参数有自车速度v、前后车距离s和前后车速度差dv。上述3个关键参数的变化直接影响驾驶人的跟车决策,驾驶人根据上述3个参数的动态变化,对自车加速度进行调整,以维持稳定的车速和安全的车距跟车行驶。前后车速度差dv的表达式如式(1)所示,其中vp为前车速度。

为量化描述跟车过程的安全与效率,现有研究中常用式(2)和式(3)所示的两个时间尺度指标进行行车效率与风险的评估。

式(2)是车头时距thw的定义,其物理意义描述的是跟车行驶的效率,车头时距越小,交通流的整体通行效率越高。式(3)是碰撞时间ttc的定义,其物理意义描述的是跟车行驶的安全性,其数值越小,表示跟车行驶的碰撞风险越大。在稳态跟车过程中,前后车的车速差dv→0,ttc→∞,故通常使用逆碰撞时间(即碰撞时间的倒数)表征碰撞风险。逆碰撞时间趋于零时,说明前后车速度差趋于零或跟车距离极大,表明此时的行车风险极小。据此,可知稳定跟车过程的车头时距趋于恒定值,而逆碰撞时间趋于零,将上述假设概括为理想的稳态跟车过程中的“两不变”规律。
为验证上述“两不变”规律的科学性,利用德国的HighD数据集进行数据的验证分析。HighD轨迹数据通过无人机在德国科隆附近的高速公路采集而得,包括110 500辆车、44 500 km行驶里程、147 h行驶时长,具有数据量大、质量高、场景丰富的特点,且该数据集中含有较多比例的货车,故可对不同货车和轿车混合模式下的异质跟车行为进行分类比较,以验证异质车型下驾驶人跟车行为的特性。从HighD轨迹文件中剔除换道和车间距大于200 m的自由流数据,并根据跟车轨迹文件中所给出的前车Id找到相应的引导车,形成跟车对。按车型的不同,将跟车分为轿车跟随轿车(Car-Car),轿车跟随货车(Car-Truck),货车跟随轿车(Truck-Car),以及货车跟随货车(Truck-Truck)4种类型,所提取的4种跟车模式的跟车对数量分别为2 370、285、340和1 036对。
图1所示为HighD数据集中4种不同跟车模式的车头时距分布图。由图1可知,不同模式下的车头时距均服从对数正态分布,不同模式下,驾驶人均倾向于以较大的概率维持恒定的车头时距行驶。将车头时距概率分布图的最大概率作为驾驶人认为理想的稳态车头时距或期望车头时距,则当前车为轿车时的两种工况,其稳态车头时距小于前车为货车的两种工况,且轿车-轿车(Car-Car)跟车模式的稳态车头时距最小,而货车-货车(Truck-Truck)模式的稳态车头时距最大。说明前车为货车时,自车驾驶人的驾驶行为趋于保守,更倾向于维持更大的车距或较小的车速跟车行驶。
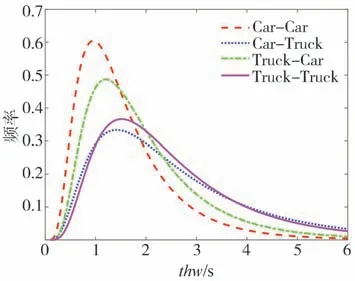
图1 各跟车模式的车头时距的统计分布
图2所示为各跟车模式下逆碰撞时间的统计分布图。由图2可知,各模式下驾驶人的逆碰撞时间为正态分布,且均值为零,说明跟车过程中驾驶人希望维持较低的碰撞风险,且自车为货车时,逆碰撞时间的概率峰值比自车为轿车时高,说明货车驾驶人对碰撞风险更敏感,因此货车驾驶人的跟车制动响应的风险阈值更低。
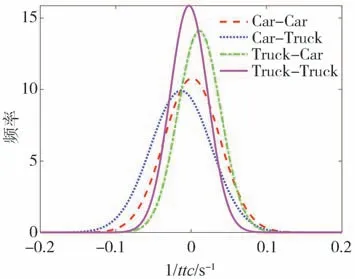
图2 各跟车模式的逆碰撞时间的统计分布
以上分别从理想跟车行为和实际跟车行为的统计特性的角度验证了不同模式下跟车行为的“两不变”规律。以下从定义出发,进一步挖掘车头时距和逆碰撞时间的数据规律。从经验数据中求解车头时距和逆碰撞时间的关键在于跟车对的前后车之间车距的估计,根据数据分析,发现跟车距离与自车的车速v呈正比,且与前后车速度差dv存在抛物线关系,本文采用式(4)所示的经验模型对跟车距离进行拟合。

图3所示是4种不同跟车模式下跟车车距的拟合效果图。4种跟车模式下跟车距离拟合的决定系数R2分别为0.783 4、0.552 4、0.763 2和0.568 3,均大于0.5。由图3和拟合优度量化指标R2的数值可知,所采用的车距模型可很好地描述自车速度和前后车速度差对跟车距离的影响。
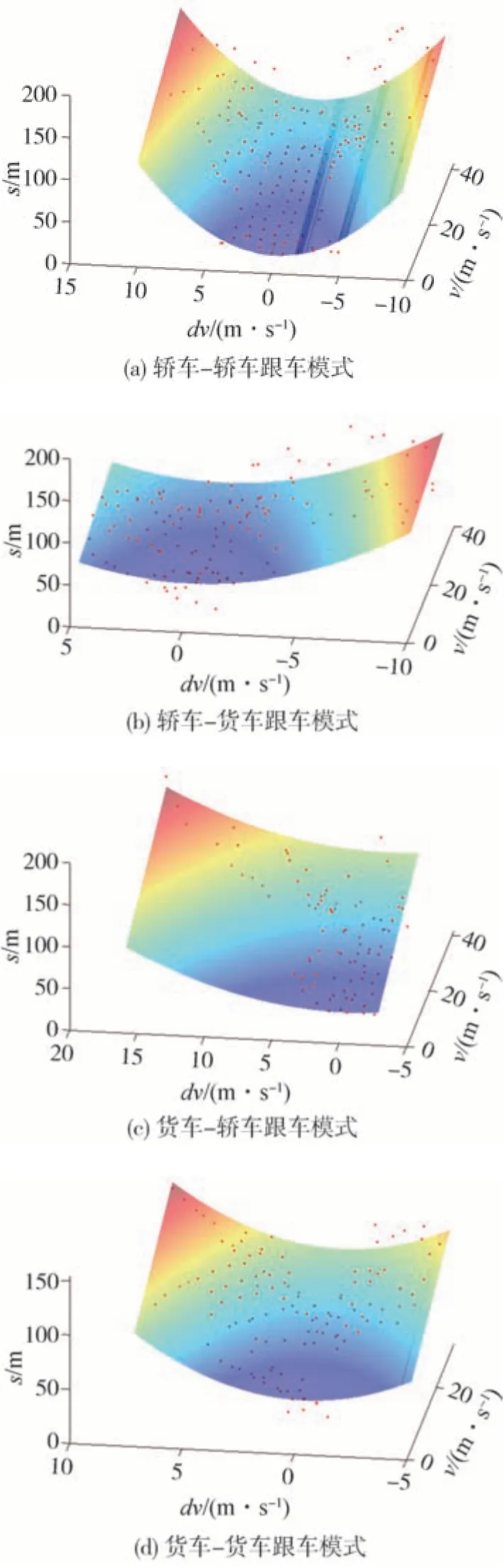
图3 车距随自车速度和速度差的变化规律
基于所提出的车距模型,进一步根据车头时距和逆碰撞时间的定义,可由式(5)和式(6)获得由跟车距离的经验模型求解的两个关键指标的表达式。
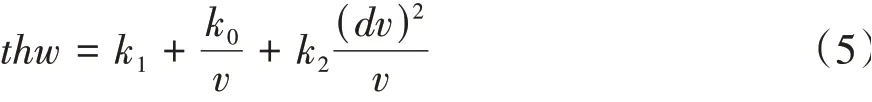
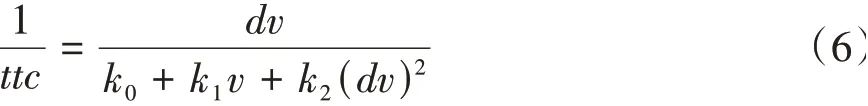
令v=20 m∕s,可由式(5)和式(6)分别计算不同速度差下的车头时距和逆碰撞时间的变化规律,如图4和图5所示。由图4可知,各模式下的跟车时距随着前后车速度差dv发生动态变化,在dv=0的稳态跟车工况下,车头时距最小,且在各种模式中,货车-货车(Truck-Truck)跟车模式的稳定车头时距最大,接近3 s,而轿车-轿车(Car-Car)跟车模式的稳定车头时距相对最小,为1.6 s。由图5可知,在dv≠0的非稳态工况下,逆碰撞时间数值非零,只有在稳态工况下,逆碰撞时间的数值才能保证碰撞风险最小。
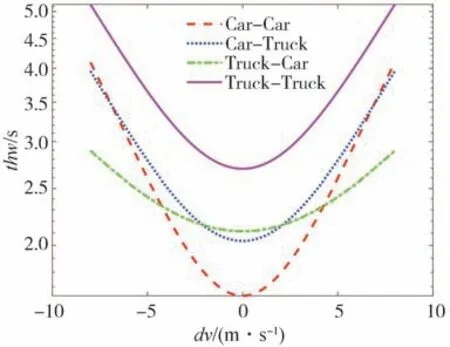
图4 非稳态工况下各跟车模式的车头时距变化
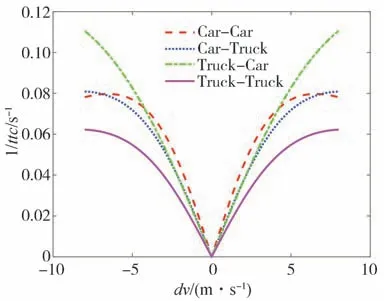
图5 非稳态工况下各跟车模式的逆碰撞时间变化
图6所示是令式(4)中的前后车速度差dv=0的稳态跟车工况下,各跟车模式的车头时距随自车车速v的变化规律。由图6可知,前车为轿车的两种跟车模式,其稳态车头时距随车速的变化不大,而前车为货车的两种跟车模式的稳态车头时距随着车速的增高略有降低。以上现象说明前车为货车时,后车的跟车行为趋向保守,在此类工况下,后车希望维持更大的车头时距,而随着前面货车速度的增大,表明整体交通流的通行顺畅程度提升,后车的车头时距才有所下降,并趋于真正恒定的稳态车头时距。
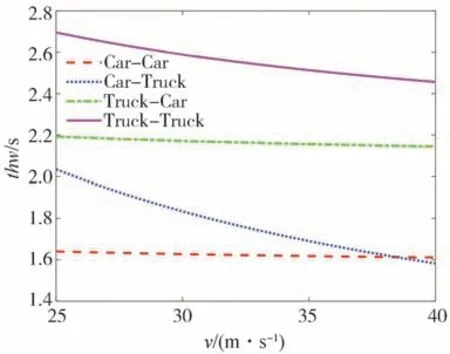
图6 稳态工况下车头时距随车速的变化规律
为进一步探索车头时距和逆碰撞时间这两个参数与不同跟车模式下的驾驶人决策响应的关系,分别将不同模式下的跟车速度v和前后车速度差dv在其最大-最小值范围内等分为20个区间,分别统计落在(v,dv)组成的联合变量区间内的数据点集的平均车速、平均车头时距、平均逆碰撞时间和平均加速度。在1ttc-1thw坐标下作出各跟车模式下的跟车加速度平均值的分类散点图,如图7所示。图中蓝色虚线为蓝色三角形数据点(跟车加速度等于零的点)的拟合直线。
由图7可知,采用1ttc-1thw坐标可对驾驶人跟车的加速度决策进行分区,在车辆的运动状态处于平衡线两侧时,驾驶人将采取加速或减速的决策,而在车辆的运动状态落入平衡线时,驾驶人保持匀速跟车行驶。值得特别指出的是,货车-轿车(Truck-Car)跟车模式下,驾驶人对风险的变化更加敏感,在加速区间内进行制动的行为增加,该模式下后车驾驶人频繁制动。
图7中,平衡线可用式(7)所示的点斜式直线方程进行拟合。式(7)中,α为斜率,β为截距。为了便于分析参数的变化规律,对式(7)进行数学变换,可转化为式(8)所示的平衡线方程。

由式(8)可见,当1ttc→0时,thw→-αβ-1,-αβ-1即为稳态跟车时距。图7的分区结果从数据上支持了驾驶人跟车行为的“两不变”规律,即在稳态的跟车过程中,驾驶人总是倾向于维持车头时距和逆碰撞时间不变,在上述两个参数发生变化时,驾驶人通过加速踏板和制动踏板的操作改变车辆的纵向加速度,从而对跟车距离和跟车车速进行动态调整,以尽快地维持稳定的跟车驾驶行为,保证车头时距和逆碰撞时间的动态平衡。
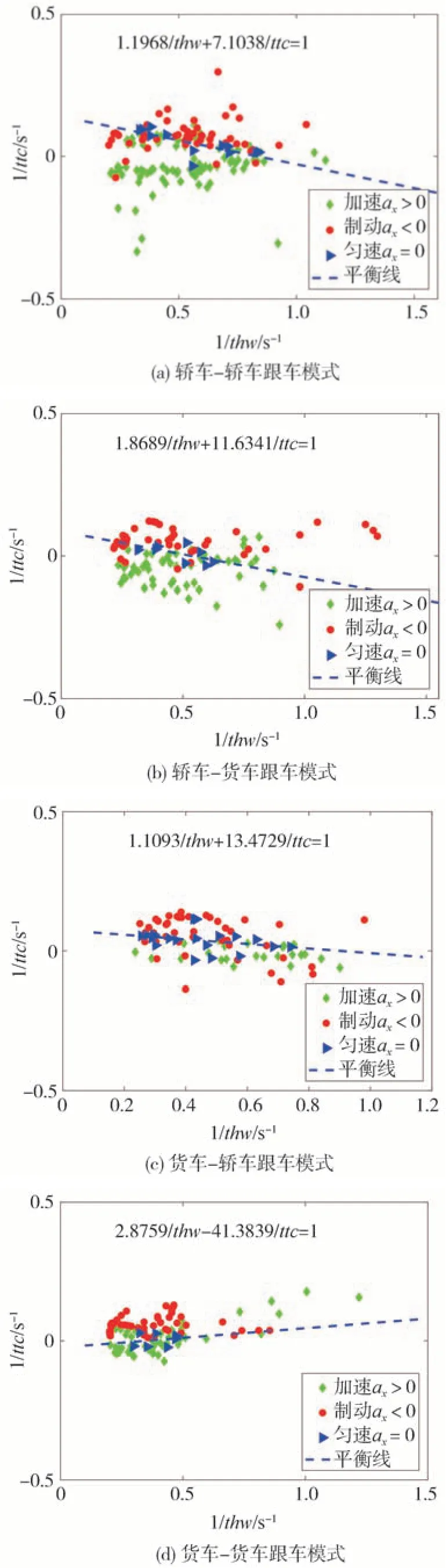
图7 跟车决策响应与风险指标的关联关系
值得特别指出的是,本文所总结出的稳态跟车过程中车头时距和逆碰撞时间这两个参数的“两不变”规律中的数值不变是宏观和统计意义上的“不变”,因此,应该从相对的和动态的角度去理解“两不变”规律。对于实际跟车行为,由于驾驶人和行驶环境的变化,驾驶人对风险的主观认知会产生动态变化,故“两不变”规律从“平衡点”向“平衡线”扩展。而平衡线的出现是由于异质车型和异质驾驶人两个方面原因共同造成的,本文数据来源于HighD数据集,考虑了异质车型对平衡线造成的影响,但无法从HighD数据中获得异质驾驶人对平衡线产生的影响,后续的研究将针对不同类型的驾驶人开展实车测试,进一步验证驾驶人在驾驶风格、驾龄、驾驶技能、性别和文化差异等因素可能对“两不变”规律产生的影响。
2 基于认知风险动态平衡的跟车决策
为了进一步从机理上探讨跟车过程中的“两不变”规律,并对跟车加速度进行量化的预测,对现有的几种典型的跟车模型进行对比分析,挖掘共性的建模规律。
式(9)为美国通用公司的跟车模型[1],式(10)为智能驾驶人(intelligent driver model,IDM)跟车模型[13],式(11)为纵向控制(longitudinal control model,LCM)跟车模型[14]。式(9)~式(11)中,λ和δ为系数,vf为交通流速度,s*(t)为理想跟车距离。
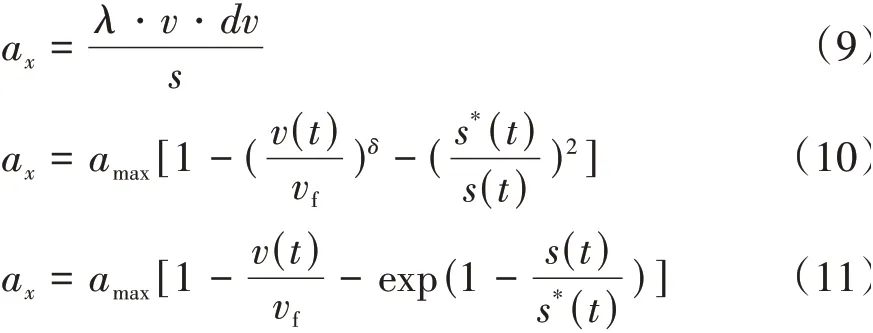
对以上3种常用的跟车模型进行一定的转换,可获得式(12)~式(14)所示的变形。式(12)~式(14)中,thw*和ttc*分别为稳态车头时距和稳态距离碰撞时间。对比式(12)~式(14)可知,跟车加速度ax都可表述为式(15)所示的普遍形式。
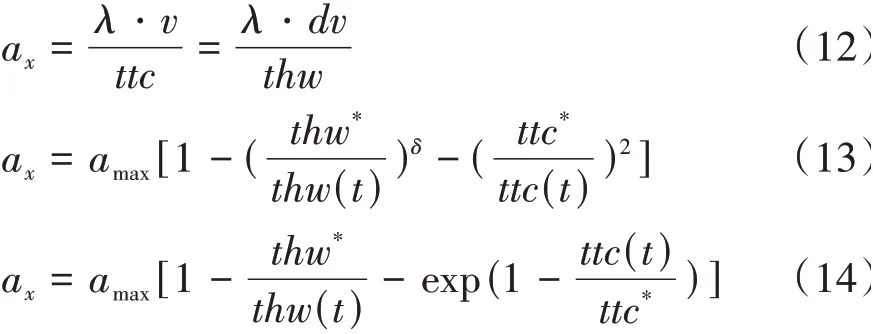

这进一步说明各种跟车模型本质上描述加速度与车头时距和逆碰撞时间这两个参数之间的映射关系。
由前文分析可知,车头时距和逆碰撞时间的线性组合可构成跟车决策分区的平衡线,为了进一步描述跟车加速度与上述两个参数的量化关系。借鉴文献[21]的思路,定义式(16)所示的认知风险函数,当RP=0时,加速度ax=0。在认知风险RP≠0时,采用式(17)的函数建立起认知风险与加速度响应的回归模型。式(17)表述的跟车模型的机理为:驾驶人通过加速踏板或制动踏板调节自车加速度,使得跟车的认知风险维持动态的平衡,在认知风险RP>0时,采取制动操作以减小行车风险,而在认知风险RP<0时则采取加速操作以提高行车效率,认知风险动态平衡的本质是跟车过程中驾驶效率和行车风险的动态平衡。
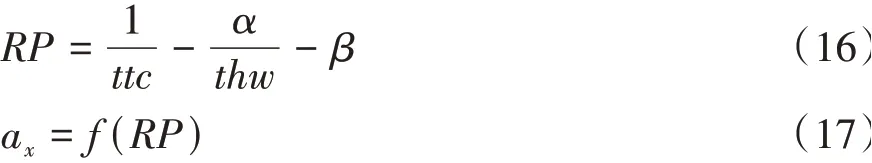
采用式(18)的线性模型建立认知风险与加速度响应的回归关系。式(18)中γ1和γ2为常数。

图8所示是加速度响应与认知风险的线性回归效果图。由图8可知,认知风险存在加减速的非对称性,在RP<0的加速区间拟合效果较好,而对于RP>0的制动减速区间,拟合效果较差。
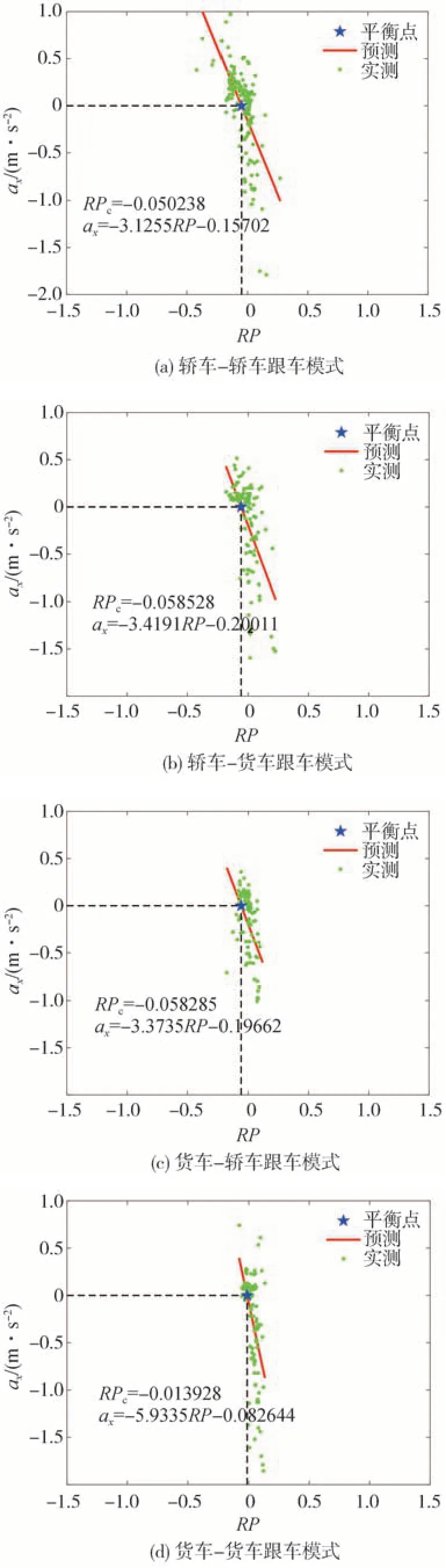
图8 加速度响应与认知风险的线性回归
为提升加速度响应与认知风险模型精度,采用式(19)所示的非线性修正模型进行建模。式(19)中η1、η2和η3为常数。
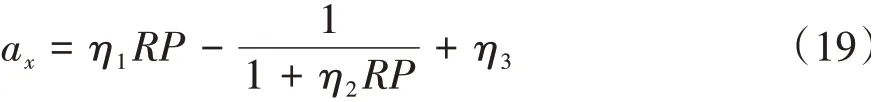
图9所示是加速度响应与认知风险的非线性回归效果图。由图9可知,引入非线性的修正项后,加速度响应的拟合优度有所提升,能够很好地描述加减速的非对称性。在RP>0的制动区间,加速度响应的斜率比加速区间的斜率更为陡峭,说明驾驶人对风险的响应更为敏感,在跟车中希望获得更为及时的制动加速度响应,而对加速的响应则希望获得平稳的加速度,以保证舒适性。综合对比图9中各模式下的建模效果可知,在货车的跟车模式下,驾驶人加速度响应的不确定性有所增加,拟合效果降低,而轿车-轿车跟车模式下加速度响应的拟合优度相对较高。
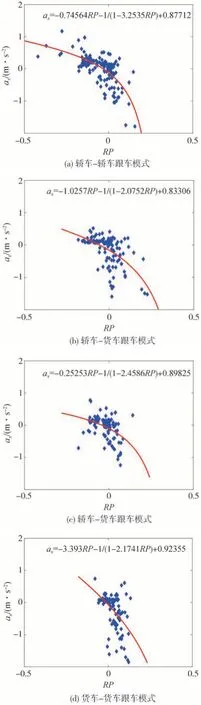
图9 加速度响应与认知风险的非线性回归
为进一步证实所提出的认知风险动态平衡的跟车模型对加速度响应非对称特性的表征能力,由式(19)对认知风险RP进行求导,获得式(20)的斜率表达式。分别取RP=±0.2位置的切线斜率作为加减速区间的加速度响应灵敏度近似值,则RP>0的减速区间的斜率计算结果如式(21)所示,RP<0的加速区间的斜率计算结果如式(22)所示。
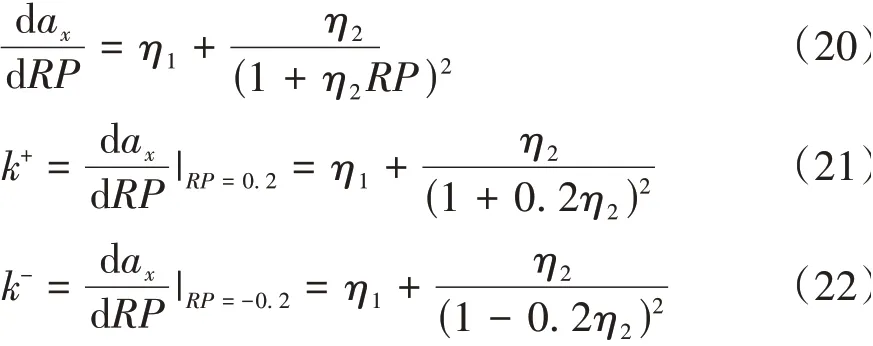
图10所示是加减速区间的加速度响应的分段斜率示意图。
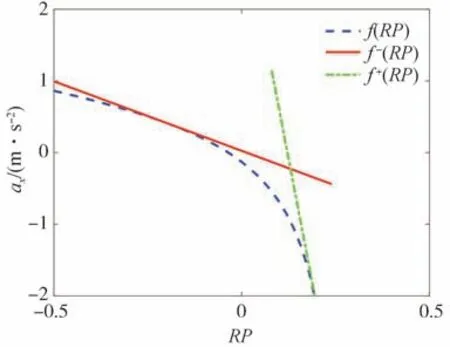
图10 加减速区间的分段近似斜率
表1所示是由式(21)和式(22)计算获得的各模式下驾驶人加速度响应在加减速区间的斜率。由表1结果可知,在加速区间内,货车-货车(Truck-Truck)跟车模式的加速度响应的斜率绝对值最大,而在减速区间内,轿车-轿车(Car-Car)跟车模式的加速度响应的斜率绝对值最大。以上现象是车辆动力学性能与驾驶人认知风险响应综合作用的结果。一方面轿车在制动性能方面有较大的优势,而货车在加速性能方面有较大的优势;另一方面,由前文的数据分析可知,轿车-轿车(Car-Car)跟车模式的稳定车头时距较小,驾驶人为保证安全,趋向于维持较大的制动强度,而货车-货车(Truck-Truck)跟车模式的稳态车头时距较大,驾驶人为追求效率,倾向于采用较大的加速度。综上所述,借鉴驾驶人在异质车型下的跟车策略,智能汽车所采取的拟人化跟车决策将维持认知风险在零点附近,当外界交通环境产生变化时,可通过不同程度的加速或减速的调节使得认知风险回归动态平衡区间,对于不同的跟车类型,加速和减速的响应敏感度也可进行实时自适应的调节,以符合乘客的心理预期。
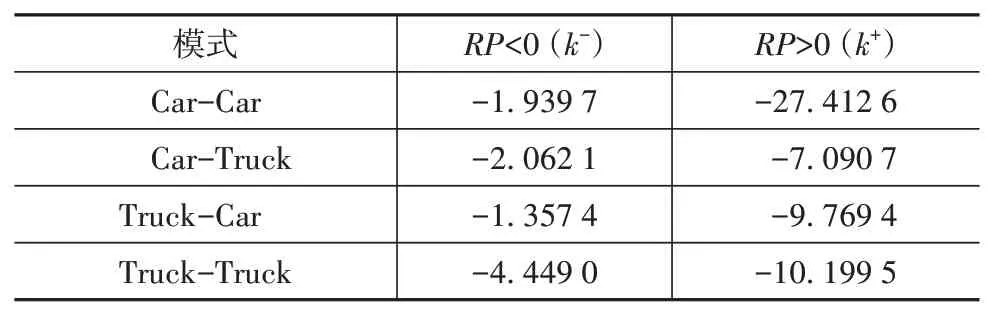
表1 各模式下加速度响应斜率对比
3 结论
针对智能汽车在异质、复杂的交通环境下跟车所面临的行车风险与驾驶效率权衡的决策难题,借鉴自然驾驶过程中驾驶人的跟车决策经验,提出认知风险动态平衡的拟人化跟车模型,有助于提升智能汽车跟车决策的科学性和合理性。主要结论如下。
(1)自然驾驶数据分析表明,跟车对的车型异质性对跟车行为产生显著影响,且跟车过程中驾驶人的跟车距离随车速和速度差不断变化,但总体上,驾驶人在稳态跟车过程中,倾向于维持跟车时距和逆碰撞时间这两个参数的“两不变”规律,以兼顾行车的安全与效率。
(2)从纵向加速度响应与认知风险映射建模的角度,提出了认知风险动态平衡的拟人化跟车模型,可用于解释“两不变”现象的机理,并实现几种典型跟车模型在数学形式上的统一。
(3)通过HighD实测跟车数据,对不同跟车模式下的认知风险平衡线进行了辨识,验证了所提出的认知风险动态平衡跟车模型可对跟车对的车型异质性进行准确的描述,说明所提出的跟车模型可满足复杂动态交通环境下拟人化的跟车驾驶需求。
后续的研究将采用更为广泛和多元的自然驾驶数据集,对不同人群在驾驶过程中认知风险所处的平衡区间的阈值进行更为深入的探索,并充分考虑其他环境因素对认知风险所产生的扰动,针对不同区域开发出符合属地人群心理预期的跟车决策算法,为加速智能汽车的推广应用提供支撑。

